立体几何有图题想图的几个着眼点

■四川省绵阳实验高级中学 邓钧方

立体几何作为综合考查同学们的直观想象、逻辑推理、数学运算和数学抽象等核心素养的重要载体，是高考数学必考内容。近年来，随着新课改的推进，命题原则逐渐从“以能力立意”转向“以素养立意”，试题正在尝试增加难度，提高能力要求。尽管如此，立体几何试题的相对难度仍属中等，是考生必争之分。

我们知道，空间想象是从研究对象或问题中抽取出数量关系或空间形式，对图形的想象主要包括有图想象和无图想象两种，是空间想象能力高层次的标志。图形作为数学表达的语言，与文字语言、符号语言配合表达数学，图形语言在直观呈现问题、数形结合解答问题、辅助空间想象问题等方面都发挥了不可替代的作用。

一、陌图化熟换视位

我们在课本中见到的柱、锥、台、球，其图形基本上都遵循斜二测规则，但在选拔性考试中，根据数学核心素养考查的需要，给出全新视角下几何体的直观图。当我们感到图形很陌生时，可以改变角度重新画一个自己熟悉的图形，这样可以快速入题。

例1（2020年浙江省“七彩阳光”新高考研究联盟三模）如图1，已知四棱锥P-ABCD 中，底面ABCD 是矩形，AB=2，PA=PB=BC =，PD=PC=。

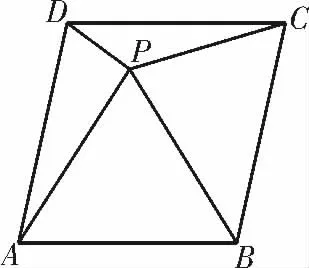
图1

（1）求证：平面PAB⊥平面PCD；

（2）求直线PA 与平面PBC 所成角的正弦值。

解析：（1）我们换一个视角画出一个熟悉的直观图。如图2，取AB，DC 的中点E，F，连接EF，PE，PF。

又AB ∥CD，所 以PE⊥CD。

又因为AB=2，所以PE=3，PF=1，所以PE2+PF2=10=BC2=EF2，即PE⊥PF。

因为CD ∩PF=F，CD ⊂平面PCD，PF⊂平面PCD，所以PE⊥平面PCD。

因为PE⊂平面PAB，所以平面PAB⊥平面PCD。

（2）设点A 到平面PBC 的距离为d。

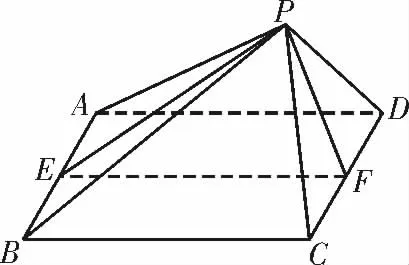
图2

由（1）知PE⊥PF，PF⊥DC。

又AB∥CD，所以PF⊥AB。

因为AB ∩PE=E，AB ⊂平面PAB，PE⊂平面PAB，所以PF⊥平面PAB。

因为AB∥CD，点C 到平面PAB 的距离为d=PF=1，所以所以

领悟：灵活利用题设条件，等效变化图形位置，常可以突破解题难点，探求出巧妙的解题方法。常见的图形位置变换方法有：①移基本图（当直观图较陌生，隐含在图形内部的线、面关系就不容易看清楚，这时可将包含有线线、线面关系的基本图形移出来观察）；②改变视角（改变看图的方向，画一个熟悉的图）；③“特写镜头”（把涉及问题的图形的关键部分画出来专门研究）。如此操作常可以得到简捷、优美的解题路径。

二、折叠成图盯不变

折叠问题多次成为高考题，所以研究其解题思路，掌握其解题方法是非常重要的。将一个平面图形翻折得到一个折叠新图，解决折叠问题的关键是紧扣折叠前后不变的“数量关系”和“线线关系”。保持不变的平行、垂直关系是证明空间线面平行、垂直关系的依据，保持不变的数量关系是求几何体有关角度、距离、面积和体积的依据。

例2（四川成都蓉城名校联盟2021届高三联考理科）如图3，AD 是△BCD 中BC 边上的高，且AB =2AD =2AC，将△BCD 沿AD 翻折，使得平面ACD ⊥平面ABD，如图4。

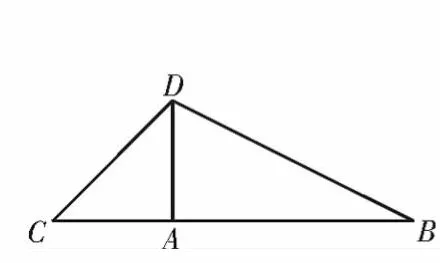
图3

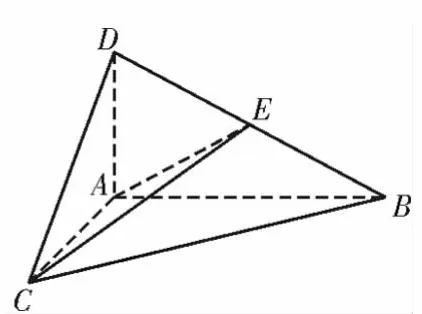
图4

（1）求证：AB⊥CD。

（2）图4 中，E 是BD 上一点，连接AE，CE，当AE 与底面ABC 所成角的正切值为时，求直线AE 与平面BCE 所成角的正弦值。

解 析：（1）由图3 知，在图4 中，AC ⊥AD，AB⊥AD。

因为平面ACD⊥平面ABD，平面ACD∩平面ABD=AD，AB⊂平面ABD，所以AB⊥平面ACD。

又CD⊂平面ACD，所以AB⊥CD。

（2）以A 为坐标原点，AC，AB，AD 所在直线分别为x 轴，y 轴，z 轴，建立如图5 所示的空间直角坐标系A-xyz，不妨设AC=1，则 A（0，0，0），B（0，2，0），C（1，0，0），D（0，0，1）。

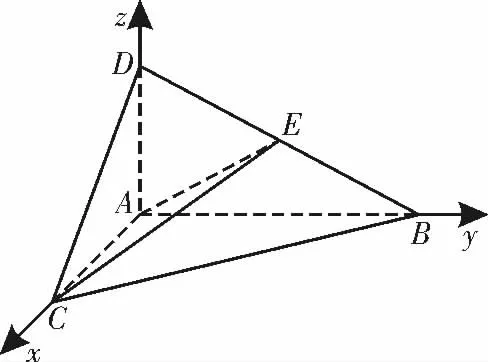
图5

领悟：折叠问题看似变化多端，实则有规律可循。在折叠前后，抓住这个动态变化过程中不变的量，如垂直、平行关系，角的大小、线段长度等，抓准了，问题就迎刃而解。

三、动态探索坐标来

我们这里讲解的立体几何动态探索问题，涉及“点”、“线”、“面”中的动态关联，有人把立体几何中的动态探索性问题分为“位置探索”、“线定面动”、“线动面定”、“线线垂直”、“线面垂直”、“面面垂直”、“线面角”和“二面角”等，但是，仔细研究运动的情形都是某点的运动，因此，只要想通“点动则线动”、“点动则面动”，那么问题就不难解决了。

例3（北京人大附中2020届高三考前热身）如图6，已知平行四边形ABCD 所在的平面与直角梯形ABEF 所在的平面垂直，BE∥AF，且为DF的中点。

图6

（1）求证：PE∥平面ABCD；

（2）求证：AC⊥EF；（3）若直线EF 上存在点H，使得CF，BH 所成角的余弦值为求 BH 与平面ADF 所成角的大小。

解析：（1）如图7，取AF 的中点Q，连接PQ，EQ。

在直角梯形ABEF中，AQ=BE=1，BE ∥AQ，所以四边形ABEQ 为平行四边形，所以AB∥EQ。

在△ADF 中，PF=PD，QF=QA，所以PQ∥AD。

又因为AD∩AB=A，所以平面PQE∥平面ABCD。

又因为PE⊂平面PQE，所以PE∥平面ABCD。

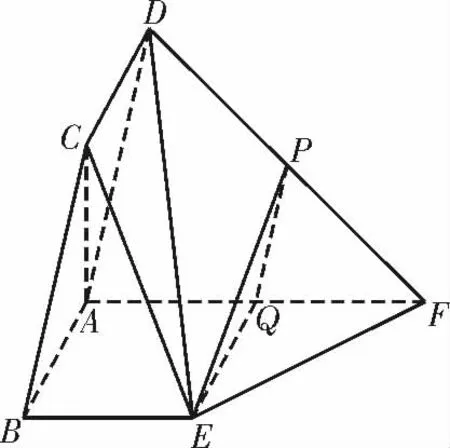
图7

又因为平面ABCD⊥平面ABEF，平面ABCD ∩平 面ABEF =AB，AC ⊂平 面ABCD，所以AC⊥平面ABEF。

因为EF⊂平面ABEF，所以AC⊥EF。

（3）由（1）（2）可建立以A 为坐标原点，AB，AF，AC 所在直线分 别为x 轴，y 轴，z轴的空间直角坐标系A-xyz，如图8。

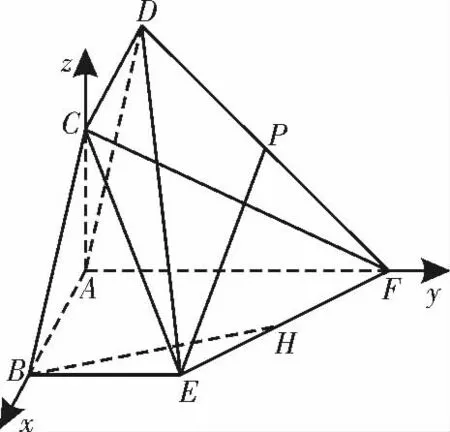
图8

领悟：①注意本题“线上动点”的向量表达：b=λa（a≠0）。②有关的存在性探索问题常利用空间向量法解决，这样可以避开抽象、复杂的寻找角的过程。只要能够准确理解和熟练应用夹角公式，就可以把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等问题。事实证明，空间向量法是解决立体几何中存在性探索问题的好方法。