用空间向量解决立体几何问题的建系策略

■四川省绵阳实验高级中学 黄 芹

立体几何是高中数学知识体系中的重要知识模块，也是高考重点考查的核心内容之一。空间向量是求解立体几何问题的一个重要工具，利用空间向量解答立体几何问题，主要突破“四关”：第一关，建系；第二关，求点的坐标；第三关，求法向量；第四关，应用公式。然而如何建立恰当的空间直角坐标系并求出点的坐标是用空间向量解决立体几何问题的关键所在。下面以典型的几何体：棱柱、棱锥、多面体为载体，以典型的问题情境设计：求线面角、求二面角、探索性问题、翻折问题为背景，剖析建立空间直角坐标系的常用途径。

途径一、利用共顶点的互相垂直的三条棱构建空间直角坐标系

例1如图1，在直三棱柱ABC-A1B1C1中，△ABC是等腰直角三角形，AC=BC=1，AA1=2，D 是侧棱AA1上的一点。

（1）证明：当D 是侧棱AA1的中点时，DC1⊥平面BCD。

图1

（2）侧棱AA1上是否存在一点D，使二面角D-BC1-C 的余弦值为若存在，请求出AD 的长度；若不存在，请说明理由。

分析：（1）几何体中有三条直线两两垂直，直接建系。（2）空间向量非常适合于解决立体几何中的探索性问题，只需要建立恰当的空间直角坐标系，通过坐标运算把“是否存在”的问题转化为“点的坐标是否有解”的问题。

解：（1）证法一：由题意BC⊥AC 且BC⊥CC1，AC ∩CC1=C，所以BC ⊥平面ACC1A1。

又因为DC1⊂平面ACC1A，所以BC⊥DC1。

又因为D 是AA1的中点，AC=AD，且∠CAD=90°，所以∠ADC=45°。

同理，∠A1DC1=45°。

所以∠C1DC=90°，则DC1⊥DC。

又因为DC∩BC=C，所以DC1⊥平面BCD。

证法二：如图2，以C为坐 标 原 点，CA，CB，CC1所在直线分别为x轴，y 轴，z 轴，建立空间直角坐标系C-xyz。

由题意知C（0，0，0），D（1，0，1），B（0，1，0），C1（0，0，2），所以

图2

所以DC1⊥CD，DC1⊥CB。

又CD∩CB=C，所以DC1⊥平面BCD。

（2）假设侧棱AA1上存在一点D 满足题意。

设AD=h（0＜h＜2），则D（1，0，h），B（0，1，0），C1（0，0，2）。

由条件易知CA⊥平面BC1C，故取m==（1，0，0）为平面BC1C 的法向量。

设平面DBC1的法向量为n=（x，y，z），所以

途径二、利用线面垂直关系，构建空间直角坐标系

例2如图3 所示，在三棱柱ABCA1B1C1中，△ABC为 等边三角形，∠BAB1=∠BB1A，AB1∩A1B=O，CO⊥平 面ABB1A1，D是线段A1C1上靠近A1的三等分点。

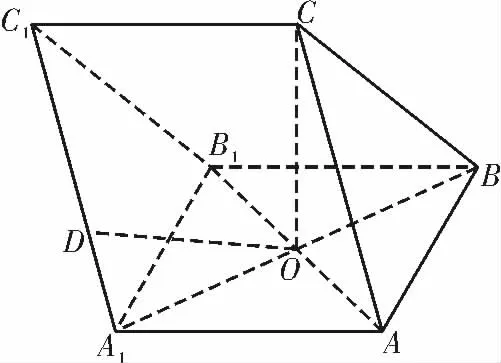
图3

（1）求证：AB⊥AA1；

（2）求直线OD 与平面A1ACC1所成角的正弦值。

分析：三棱柱放倒，但仍有使用向量法的明显特征，由条件可得四边形A1ABB1为菱形，菱形的对角线互相垂直，结合已知条件中的线面垂直关系：CO⊥平面ABB1A1，所以可以以O 为坐标原点建系。由第（1）问的结论也可以B 为坐标原点，z 轴与OC 平行（z 轴悬空）建系，如图4所示。求点C的坐标可以利用求 点D的坐标可以利用本题第（2）问的解答以O 为坐标原点建系为例。

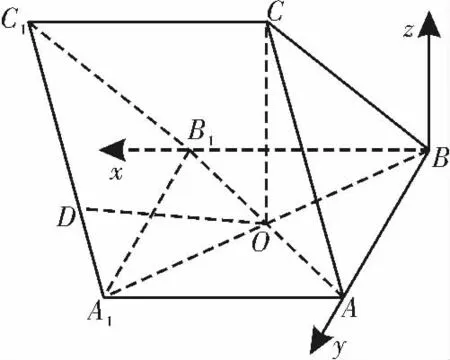
图4

解：（1）因为∠BAB1= ∠BB1A，所以AB=BB1，所以四边形A1ABB1为菱形。

因为CO⊥平面ABB1A1，故∠COA=∠COB=90°。

因为CO=CO，CA=CB，所以△COA≌△COB，所以AO=BO，即四边形ABB1A1为正方形。

所以AB⊥AA1。

（2）依题意，CO⊥OA，CO⊥OA1。

在正方形A1ABB1中，OA1⊥OA。

所以以O 为坐标原 点，OA1，OA，OC 所在直线分别为x 轴，y 轴，z 轴，建立如图5 所示的空间直角坐标系O-xyz。

图5

不妨设AB=2，则O（0，0，0），A1（，0，0），A（0，，0），

设平面A1ACC1的法向量为m=（x，y，z），所 以令x=1，得y=1，z=1，所以m=（1，1，1）。

所以直线OD 与平面A1ACC1所成角的正弦值为

总结：建系的关键是找到垂直关系。判断线线垂直的常用结论：正方形、矩形、直角梯形；等腰三角形底边上的中线与底边垂直；菱形的对角线相互垂直；勾股定理逆定理；线面垂直性质定理等。

途径三、利用面面垂直关系，构建空间直角坐标系

例3如图6，在四棱锥P-ABCD 中，底面ABCD 为直角梯形，BC∥AD，AD ⊥DC，BC=CD=1，AD=2，PA=PD，E 为PC 的中点，平面PAD ⊥平面ABCD，F 为AD 上一点，PA∥平面BEF。

（1）求证：平面BEF⊥平面PAD；

（2）若PC 与底面ABCD 所成的角为60°，求二面角E-BF-A 的余弦值。

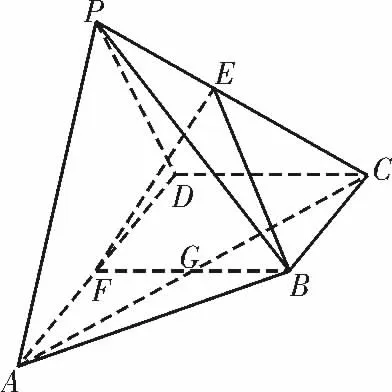
图6

分析：（1）连接AC 交BF 于点G，连接EG，结合线面平行的性质可得PA∥EG，再由E 为PC 的中点，得G 为AC 的 中点，则△AFG≌△CBG，得到AF=BC=AD=1，即F 为AD 的中点，可得四边形DCBF 为平行四边形，再由AD⊥DC，得BF⊥AD，可得BF⊥平面PAD，进一步得到平面BEF⊥平面PAD。（2）由面面垂直转化为线面垂直，结合底面是直角梯形，可以以D 为坐标原点建系。分析得到F 为AD 的中点，也可以以F 为坐标原点建系。P 点坐标未知，需要先设坐标，比如设P（0，0，t），由PC 与底面ABCD 所成的角为60°可求解t。

解：（1）连接AC 交BF 于点G，连接EG。

因为PA∥平面BEF，PA⊂平面PAC，平面PAC∩平面BEF=EG，所以PA∥EG。

又E 为PC 的中点，所以G 为AC 的中点，则△AFG≌△CBG，得AF=BC=AD=1，所以F 为AD 的中点。

因为BC∥FD，且BC=FD，所以四边形DCBF 为平行四边形。

因为DC⊥AD，所以BF⊥AD。

又BF⊂平面ABCD，平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，所以BF⊥平面PAD。

又因为BF⊂平面BEF，所以平面BEF⊥平面PAD。

（2）连接PF，因为PA=PD，F 为AD的中点，所以PF⊥AD。

又PF⊂平面PAD，平面PAD ⊥平面ABCD，平面PAD∩平面ABCD=AD，所以PF⊥底面ABCD。

又BF ⊥AD，所以以F 为坐标原点，FA，FB，FP 所在直线分别 为x 轴，y 轴，z 轴，建立空间直角坐标系F-xyz，如图7所示。

设P （0，0，t），则F（0，0，0），C（-1，1，0），

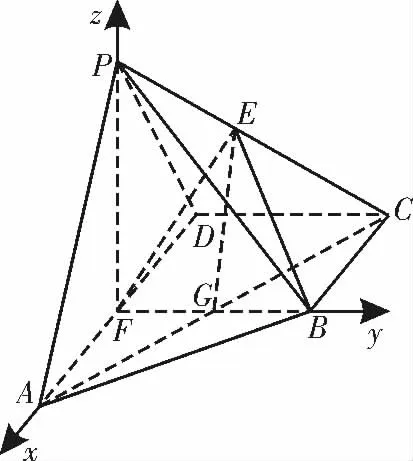
图7

取平面ABCD 的法向量为n1=（0，0，1），所以

设平面EBF 的法向量为n2=（x，y，z），所 以令z=1，得x=，所以n2=（，0，1）。

总结：先由面面垂直性质定理得到线面垂直，再建立空间直角坐标系。建系时让一些点、线段尽量与坐标轴重合。在利用法向量解决线面角及二面角大小时，一定要注意正确运用公式，并判断所求二面角是钝角还是锐角。

立体几何解答题通常分步设问，既考查同学们的空间想象能力与逻辑推理能力，也考查运算求解能力。问题情境千变万化，但万变不离其宗的是：立体几何解答题的考查归结为点、线、面的位置关系，以及角度、距离的求解。空间向量工具是解决立体几何问题的“尚方宝剑”，空间直角坐标系是“定海神针”，三种建系途径若能熟练掌握，定能提高分析问题的能力和解题速度。