空间向量应用的误区提醒

■山东省单县第一中学 王庆敏

空间向量是解答立体几何问题的有力工具，问题求解的过程是通过建立空间直角坐标系，引入点的坐标，表示出相关向量，将距离、平行、垂直、夹角问题转化为相应的向量关系问题。但同学们在应用空间向量解题时，常会由于建系不合理、混淆有关概念、过程不规范等原因，造成错误。本文总结了几类典型的易错点，给予提醒。

一、建系不合理或盲目建系

建立空间直角坐标系是应用空间向量解题的“起点”，通过恰当建系、准确求出点的坐标，再表示出相应向量，进而利用向量的关系求解空间几何问题。但要注意的是解题时要避免盲目建系，小题大做（证明平行、垂直一般不需要建系；求解距离时很少建系；在易作平行线求异面直线所成的角、易作平面的垂线求线面角、易作交线的垂线求二面角时可不用建系）。

例1（吉林长春2020届高三质量监测（三））如图1所示，在四棱锥P-ABCD 中，底面ABCD 为直角梯形，BC∥AD，AD⊥DC，BC=CD=1，AD=2，PA=PD，E 为PC 的中点，平面PAD ⊥平面ABCD，F 为AD 上一点，PA∥平面BEF。

（1）求证：平面BEF⊥平面PAD；

（2）若PC 与底面ABCD 所成的角为60°，求二面角E-BF-A 的余弦值。

解析：（1）如图1，连接AC 交BF 于G，连接EG，因为PA∥平面BEF，PA ⊂平面PAC，平面PAC∩平面BEF=EG，所以PA∥EG。

又E 为PC 的中点，所以G 为AC 的中点，由△AFG≌△CBG，可得AF=BC=1=，所以F 为AD 的中点。

图1

因为BC∥FD，且BC=FD，所以四边形DCBF 为平行四边形。

因为AD⊥DC，所以BF⊥AD。

又BF⊂平面ABCD，已知平面PAD⊥平面ABCD，平面PAD ∩平面ABCD =AD，故BF⊥平面PAD。

又BF⊂平面BEF，所以平面BEF⊥平面PAD。

（2）连接PF，因为PA=PD，F 为AD的中点，所以PF⊥AD。

又PF⊂平面PAD，平面PAD ⊥平面ABCD，平面PAD∩平面ABCD=AD，所以PF⊥底面ABCD。

又BF⊥AD，所以以F 为坐标原点，FA，FB，FP 所在直线为x 轴，y 轴，z轴，建立如图2 所示的空间直角坐标系F-xyz。

设P（0，0，t），C（-1，1，0），取平面ABCD 的法向量为n1=（0，0，1）。

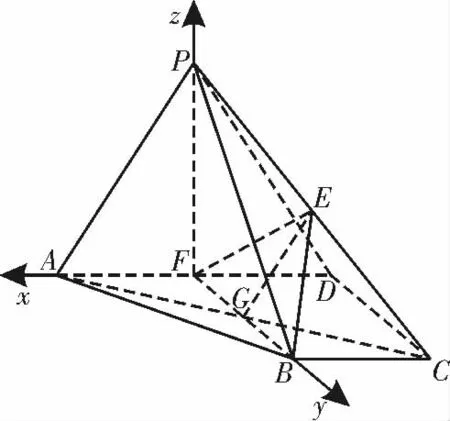
图2

设平面EBF 的法向量为n2=（x，y，z），则

误区提示：恰当建立坐标系是使计算简捷的有力保障，如果建系不合理，会导致点的坐标无法求出或不易求得，向量无法表示，进而使计算过程较为烦琐，甚至可能出现无法计算出结果的情况。解答本题时，同学们的建系方式五花八门，有一部分同学把点B 或D 视为空间直角坐标系的坐标原点，导致某些点的坐标不易求解，陷入解题误区。

二、过程不严谨

建立空间直角坐标系时，要选择两两垂直的三条直线为坐标轴，但这种垂直关系往往不会直接给出，而是需要先证明后再应用。

例2（2020 年 江 苏徐州高三月考）如图3，在四棱锥E-ABCD 中，底面ABCD 是圆内接四边形，CB=CD=CE=1，AB=AD=AE =，EC⊥BD。

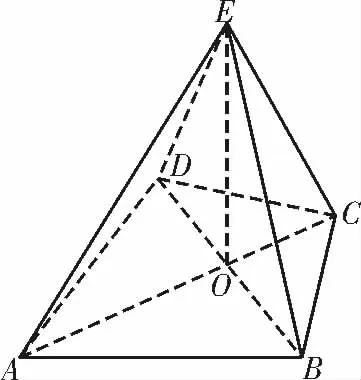
图3

（1）求证：平面BED⊥平面ABCD；

（2）若点P 在平面ABE 内运动，且DP∥平面BEC，求直线DP 与平面ABE 所成角的正弦值的最大值。

解析：（1）如图3，连接AC，交BD 于点O，连接EO。

因为AD=AB，CD=CB，AC=AC，所以△ADC≌△ABC，易得△ADO≌△ABO，所以∠AOD=∠AOB=90°，所以AC⊥BD。

又EC⊥BD，EC∩AC=C，所以BD⊥平面AEC。

又EO⊂平面AEC，所以OE⊥BD。

又底面ABCD 是圆内接四边形，所以∠ADC=∠ABC=90°，在Rt△ADC 中，由AD =，CD=1，可得所以易得△AEO∽△ACE，所以∠AOE=∠AEC=90°，即EO⊥AC。

又AC，BD ⊂平面ABCD，AC∩BD=O，所以EO⊥平面ABCD。

又EO⊂平面BED，所以平面BED⊥平面ABCD。

（2）如图4，取AE 的中点为M，AB 的中点为N，连接MN，ND，DM，则MN∥BE。

由（1）知∠DAC=∠BAC=30°，即∠DAB=60°，所以△ABD 为正三角形，所以DN⊥AB。

又BC⊥AB，所以DN ∥BC，所以平面DMN∥平面EBC，所以点P 在线段MN 上。

以O 为坐标原点，建立如图4所示的空间直角坐标系O-xyz，则

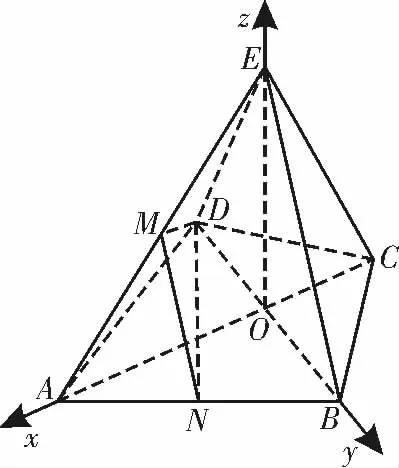
图4

误区提示：空间直角坐标系的建立要充分利用题目中直接或间接给出的线线垂直关系，本题中给出了矩形、等腰三角形，因此可利用相关图形的性质得到线线垂直关系。类似地，若题目条件中含有菱形，则可利用其对角线互相垂直得到线线垂直关系。但要注意，在问题的求解中利用这些关系建立坐标系时，要给出必要的说明。

三、忽视线面角与向量角的关系

线面角是直线与其在平面内的投影的夹角，而利用空间向量求线面角时，通常求出的是直线的方向向量与平面法向量的夹角，要注意二者的关系。

例3（2020年贵州遵义高三期中（理））如图5，正方形AMDE 的边长 为2，B，C 分别为边AM，MD 的中点，在五棱锥P-ABCDE 中，F 为 棱PE 的中点，平面ABF 与棱PD，PC 分别交于点G，H。

（1）求证：AB∥FG；

（2）若PA ⊥底 面ABCDE，且PA=AE，求直线BC 与平面ABF 所成角的大小。

解析：（1）在正方形AMDE 中，因为B是AM 的中点，所以AB∥DE。

图5

（2）因为PA ⊥底 面ABCDE，所以PA⊥AB，PA⊥AE，如图6，建立空间直角坐标系A-xyz，则 A（0，0，0），B（1，0，0），C（2，1，0），P（0，0，2），F（0，1，1）=（1，1，0）。

图6

误区提示：线面角与直线的方向向量和平面法向量的夹角（锐角）是互余的关系，部分同学在求解此类问题时，因忽略这种关系会将线面角的求解公式记为cosθ=正确的线面角求解公式是其中l，n 分别表示直线的方向向量和平面的法向量。

解决关于向量问题时，一要善于运用向量的平移、伸缩、合成、分解等变换，正确地进行向量的各种运算，加深对向量的本质的认识。二是向量的坐标运算体现了数形结合的思想。用空间向量解决立体几何问题一般可按以下过程进行思考：①要解决的问题可用什么向量知识来解决? 需要用到哪些向量?②所需要的向量是否已知? 若未知，是否可用已知条件转化成的向量直接表示? ③所需要的向量若不能直接用已知条件转化成的向量表示，则它们分别最易用哪个未知向量表示? 这些未知向量与由已知条件转化的向量有何关系? ④怎样对已经表示出来的所需向量进行运算，才能得到需要的结论? 从立体几何解答题的答题情况看，同学们出现“会而不对，对而不全”的现象严重（解题中论述不严格，条理不清，缺条件，因果关系不成立等）。在平时的训练中，要注重思维的条理性和表达的规范性，做到分析问题有理有据，表达论证合规合矩。在立体几何解答题的作答中，防止出现“跳”（步），“离”（图形与书写相脱离），“省”（省略关键步骤）等现象。乍一看，结果（论）正确，似乎没有问题，但经不起仔细推敲。在平时训练中，要做到：符号语言要规范，表达要严谨（建系的说明）。分分必争！ 对照历年高考阅卷的评分细则和评分标准严格做到解题步骤书写规范，踩点得分，分步得分。要实现：想得清楚，说得明白，写得干净。