基于互相关和Hilbert的多设备测试数据延时研究及优化

杨刚 彭冲 王倩 钟欣

（1.重庆车辆检测研究院有限公司，国家客车质量监督检验中心，重庆 401122；2.汽车主动安全测试技术重庆市工业和信息化重点实验室，重庆 401122；3.电动汽车安全评价重庆市工业和信息化重点实验室，重庆 401122）

主题词：互相关函数 延迟时间 Hilbert 趋势项

1 前言

在汽车检测工作中，常需利用多个实验室的检测设备对一台样车进行比对试验，并对不同设备采集的数据进行分析和评价。设备比对试验的目的是确定实验室的能力以及保证测试结果的准确性，在企事业、专业质检、校准机构的实验室中广泛开展[1]。

陀螺仪是目前汽车整车研发认证过程中经常使用的测试仪器[2-3]，可有效实现汽车加速度、俯仰角、横摆角等多个参数的测量。很多数据采集器无法一次接入多个陀螺仪进行比对试验，直接分析陀螺仪信号会产生较大的时间延迟，造成分析数据的失真，从而影响试验分析结论的准确性。

时间延迟估计早期主要应用在声学领域，目前，对信号进行时间延迟估算的方法主要有阈值法、互相关函数法和小波分析法[4]。阈值法首先设置一个阈值，当传感器采集的信号到达阈值时，通过平移信号来校准延时。对噪声较大的信号，该方法误差较大。小波分析法需要选取合适的小波[5]，故该方法应用较少。互相关函数广泛用于求解不同信号的延迟，计算的结果具有较好的准确度[6-8]，而对互相关函数进行Hilbert 差值计算有利于提高其锐度[9-10]，延迟时间估计更准确，但是当信号趋势项较大，而信号波动较小时，上述方法计算的延迟时间误差较大。因此，本文提出基于互相关函数和Hilbert 差值的试验数据时间延迟优化算法。先将信号利用最小二乘法拟合去除趋势，再通过互相关函数和Hilbert 差值计算仿真信号延迟时间，并进行分析，最后用试验数据验证方法的准确性。

2 Hilbert差值延时估计的原理

利用信号的互相关函数，可以计算2个信号的延迟时间，但是对于信噪比较小的信号，直接用互相关函数无法准确地计算2 个信号的延迟时间，无法使信号同步。因此，当信噪比较低时，可以利用Hilbert 差值来计算延迟时间，其原理图如图1 所示。其中，x1(t)和x2(t)分别为采集有延迟时间的2个信号。

图1 Hilbert差值计算延迟时间原理

2.1 最小二乘法拟合去除趋势项

采集的测试数据反映了试验的状态，但数据中趋势项的存在会妨碍后续分析，因此需要去除趋势项，常见的方法是对信号进行最小二乘法多项式拟合[11]，根据信号的复杂程度选择多项式拟合的阶次。信号的趋势项多为非线性趋势，需使用阶次较高的多项式，并用原信号减去其趋势项。

2.2 互相关函数

离散信号互相关函数相当于不停地平移信号再做内积[6]，将离散信号每次移动1个点后计算内积，当平移的点数靠近延迟时间对应的点数时，内积计算的结果取得最大值。再根据该最大值找到对应的平移点数，从而计算出延迟时间。

2.3 Hilbert差值

经过Hilbert 变换后得到的信号发生90°相移，频域各频率分量的幅度保持不变。此外，Hilbert变换后信号峰值对应的点接近零，而周围的信号是非零的。将2个信号的互相关函数经过Hilbert 变换后，可以将寻找互相关函数的峰值转换为寻找零点，但是实际操作中，当信号出现多个零点时，判定真实延迟时间较为复杂。

将原信号减去Hilbert 变换后的绝对值可以降低周围信号的幅值，突出峰值信号，这便是Hilbert 插值计算延迟时间的原理。这样计算的结果在噪声较大时会突出峰值，是对利用互相关函数求延迟时间的优化。

3 仿真计算与分析

采用陀螺仪进行比对试验，按照GB/T 6323—2014进行稳态回转试验，采用转向盘转角固定，缓慢增加车速的方式开展试验。仿真模拟的信号先采用接近实际试验的数学模型，再在仿真信号上加入高斯白噪声，并进行延迟时间估算，验证方法的有效性。

3.1 数学模型建立及仿真分析

稳态回转试验中，车辆的侧向加速度先缓慢上升，到达稳定值后保持基本不变，随着试验的结束快速降低。故为了更加贴近实际试验，设车辆侧向加速度仿真数学模型为分段函数，其表达式x(t)为：

式中，β～N(0,0.22)。

为了使仿真与试验的信号一致，设信号采样频率fs=100 Hz。为了模拟2个陀螺仪采集的实际数据，将x(t)分别加上信噪比为30 dB的高斯白噪声，产生2个信号，并将信号2 前3 s 的数据截去，生成的信号分别为s1(t)、s2(t)，如图2所示。

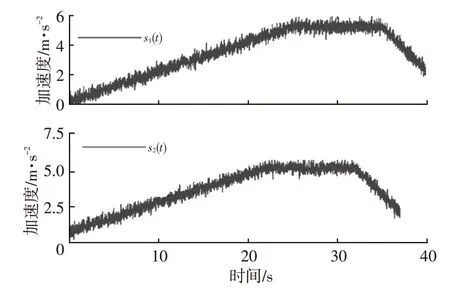
图2 仿真信号s1(t)和s2(t)

3.2 数据计算与分析

采用20次多项式进行最小二乘法拟合，信号s1(t)趋势曲线如图3所示，与图2对比可知，趋势曲线与原信号基本接近。将去除趋势后的信号先求互相关函数，再按照Hilbert差值进行计算，结果如图4所示。

图3 信号s1(t)趋势曲线

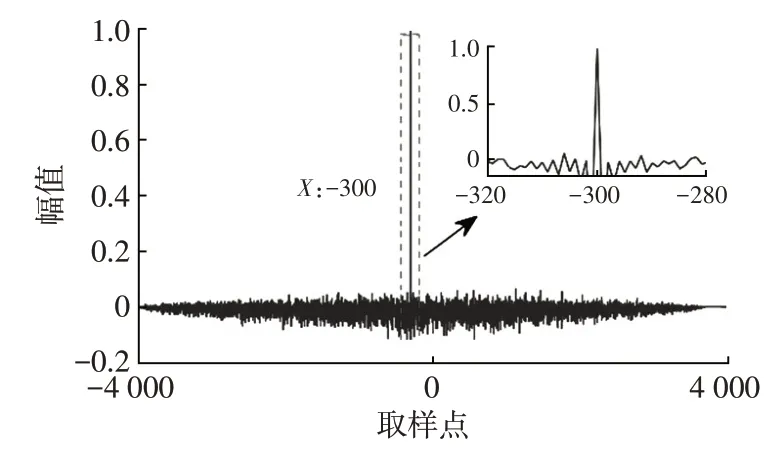
图4 优化算法延时计算

将信号s1(t)和s2(t)做互相关函数和Hilbert 差值，计算的结果除以结果中的最大值进行归一化，归一化后幅值如图5 所示。由图5 可知，互相关函数法和Hilbert差值计算的延时为300 个采样点，由于采样频率为100 Hz，计算的延时为3 s，与仿真信号一致。并由图5可知，Hilbert差值得到的幅值更加突出延时点对应的峰值，降低了周围数据点的幅值，使计算更加准确。对比图4和图5，2种方法都能计算出准确的延迟时间，但是去除趋势后计算的幅值使延时信号更突出，从图4中的放大图可以清晰地看出，只有在采样点-300 时出现最大值，附近的值都接近0，这使得计算结果更加准确。

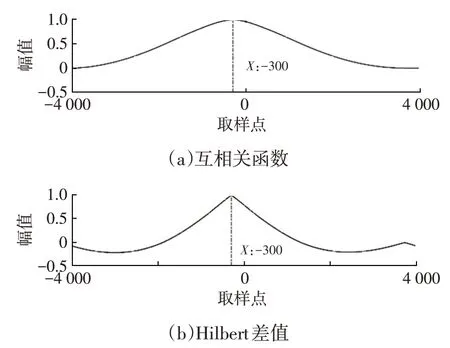
图5 仿真信号延时计算

4 试验测试及算法验证

为了进一步验证优化算法计算延迟时间的准确性，将试验采集的陀螺仪信号通过CAN接口转接到同一个数据采集器，截取采集的信号，用计算的延迟时间与截取时间的误差进行比较来验证方法的准确性。

4.1 试验测试

比对试验中，陀螺仪均采用英国Oxts 公司生产的RT3002 型机械陀螺仪，可设定各陀螺仪的相对位置。为了达到所有陀螺测试车辆同一点的状态，固定其中1个陀螺仪作为基准位置，测量各机械陀螺仪的相对位置，并将其设置于陀螺仪的坐标参数，从而保证各陀螺仪测试点为同一位置。基于日常整车试验测试情况，设定各陀螺仪的采样频率为100 Hz，将陀螺仪信号通过CAN转给数据采集仪器（德国IMC 公司生产的通用数据采集器），陀螺仪的安装和数据采集器的连接如图6所示。

图6 试验设备

4.2 侧向加速度信号延时计算与分析

采用某客车进行测试，比对多个陀螺仪测量车内同一点的车辆侧向加速度信号，验证优化算法计算延迟时间的准确度。测试车辆安装转向测试仪进行稳态回转试验，测试过程中固定转向盘转角进行加速，保证其与目标转角差异在±5°以内，以最低稳定车速在直径大于30 m 的环形通道行驶。测试过程中缓慢增加车速（采用同一挡位），直至车辆侧向加速度达到4 m/s2并稳定10 s，然后结束该次试验。

因为数据采集器的CAN接口有限，将其中2个陀螺仪的数据转接给IMC 数据采集器。记陀螺仪1 的侧向加速度为y1(t)，截去陀螺仪2 前4 s 的侧向加速度数据，记为y2(t)，如图7所示。

为了使计算更加精准，突出延时点对应的峰值，先将信号拟合去除趋势。采用最小二乘法多项式拟合，为了更接近侧向加速度数据的趋势，此处采用50 次多项式拟合，信号y1(t)趋势曲线如图8 所示，与图7 的y1(t)曲线对比可知，趋势曲线与原信号基本接近。

将去除趋势的侧向加速度按照优化算法进行计算的结果如图9所示，直接将加速度信号用互相关函数计算的结果如图10 所示。对比图9 和图10，二者都可以根据采样点-400 除以采样频率100 Hz，计算的延时为4 s，可以验证2 种计算延时方法的正确性。去除趋势后计算的幅值使延时信号更突出，图9中的放大图可以清晰地看出在采样点-400时出现最大值且附近的值都接近0，不会影响最大值对应的采样点的判断，而图10中-400附近的值均接近1，当最大值对应的采样点判断错误，可能导致根据该方法计算的延迟时间出现误差。

图7 加速度信号y1(t)和y2(t)

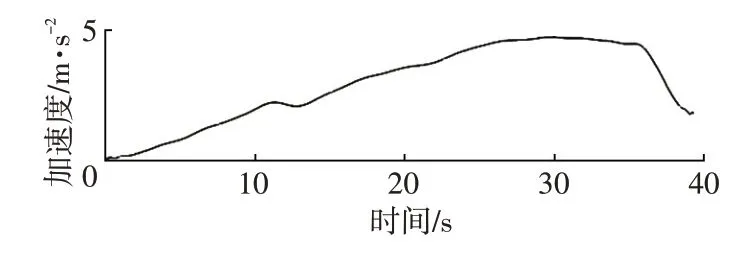
图8 加速度信号y1(t)趋势曲线

图9 优化算法延时计算

图10 加速度直接互相关函数延时计算

4.3 车速信号延迟时间计算与分析

RT 机械陀螺仪安装差分天线后速度误差很小，为了验证优化算法用于计算陀螺仪车速信号延迟时间的准确性，将2 个陀螺仪的数据转接给IMC 数据采集器。记陀螺仪1 的车速数据为z1(t)，截去陀螺仪2 前5 s 的车速数据为z2(t)，如图11所示。

图11 速度信号z1(t)和z2(t)

采用50 次多项式拟合后信号z1(t)的趋势曲线如图12 所示，与图11 的z1(t)曲线对比可知，趋势曲线基本接近原信号的趋势。

图12 速度信号z1(t)的趋势曲线

将去除趋势的车辆速度按照优化算法进行计算，结果如图13 所示，直接将速度信号用互相关函数计算的结果如图14所示。

图13 优化算法的延时计算

图14 速度直接互相关函数延时计算

对比图13 和图14，优化算法计算的幅值最大值对应的采样点是-500，峰值明显，计算得到延时为5 s。而直接用互相关函数计算的采样点是-470，计算得到的延迟时间是4.7 s。由图14 的放大图可知，互相关函数计算的最大值附近的点均较为接近，导致噪声较大时出现最大值位置并非实际延迟时间对应的采样点，最大值对应的采样点判断错误时，会使计算的延迟时间出现误差。试验验证了优化算法计算延迟时间方法的准确性，而直接互相关函数计算延迟时间存在误差。

5 结束语

本文改进了一种延迟时间算法的估计方法，先去除原始数据中的趋势项，再利用Hilbert 差值法和互相关函数法计算延迟时间算法，建立了与试验车辆侧向加速度信号形式相同的仿真信号。分别用优化算法和自相关函数计算延迟时间，结果表明，2 种方法都能计算出准确的延迟时间，但是优化算法计算的幅值更加尖锐，使最大值更加突出，得到更加准确的延迟时间。

通过在装有陀螺仪的某客车上进行实车试验，分别对侧向加速度和车速信号进行延迟时间计算，采用优化算法和互相关函数法进行延迟时间计算，试验结果表明，优化算法计算的延迟时间准确，而直接互相关函数计算延迟时间存在误差。