基于需求时间的隧道塌方应急资源分级调度研究*
李 霞,李佳璇,崔洪军,朱敏清
(1.河北工业大学 土木与交通学院,天津 300401; 2.河北工业大学 建筑与艺术设计学院,天津 300401)
0 引言
隧道塌方是公路隧道修建过程中发生频率最高且危害最大的事故,严重威胁施工人员的生命安全,造成巨大财产损失。
针对救援时间的应急资源调度研究,田晓勇等[1]对车辆运输时间进行修正,建立基于灾害抢修的调度优化模型;Chai等[2]考虑排队延误,提出基于救援路径出行时间估计的资源调度方法;Chi等[3]设计时效性评价函数作为目标函数,进行应急资源调度研究;Deng等[4]基于混合时间窗,建立多式联运最优路径模型;吕伟等[5]考虑物资需求紧迫程度差异,建立软硬时间窗综合约束的多目标路径方案生成模型。上述学者从运输时间修正、时效性函数、时间窗约束等方面对救援时间提出严格区间要求,较少考虑其他考量因素。因此,本文提出需求时间概念,象征性划定救援覆盖区域范围,放宽对物资送达时间的绝对性要求,能更好地包容其他关键考量因素,综合寻找最优方案。
针对应急资源调度问题的研究,在路径决策方面,时间是救援工作能否成功的关键,朱莉等[6]、Cao等[7]考虑以最小化运输时间作为决策目标。本文在此基础上,引入需求时间约束;另外,物资调度需要相对畅通的道路条件,因此将畅通可靠度作为另一考量因素,并引入可靠度阈值约束。在资源调度方面,田志强等[8]、王薇等[9]以最小化应急救援结束时间和调度费用为目标,建立双目标应急调度优化模型;宋少忠等[10]以满足供应点需求的供应点数量最少为目标,建立资源调配模型。综上研究,本文在考虑时间、成本和供应点数量基础上,提出救援效率概念,建立最小化调度成本和最大化救援效率的双目标优化模型,不仅可减少目标数量、降低求解复杂度,而且更能体现救援能力、对比可行方案的优劣。
本文基于需求时间,采取需求时间服务范围多级调度方案,服务范围内若物资满足要求,优先在该范围内进行资源调度;若某物资种类不能满足救援需求,则逐级扩大范围寻找新供应点,并通过制定特定供应点与需求点间该物资运输路径上的应急交通管控预案,尽最大可能提高运输道路畅通程度,保障救援时间。
1 救援需求时间
1.1 需求时间与资源调度时间的联系
假设任一可行救援方案中所有供应点的物资全部抵达后,才认为有效救援。将需求时间视为资源调度时间的约束,建立关系如式(1)~(2)所示:
T(Φs)≤X
(1)
(2)

1.2 需求时间确定
需求时间指从被困人员角度出发,在塌方发生后在规定的时间点内相关救援人员及车辆必须抵达事故现场并展开救援,以尽可能保证被困人员满足心理、生理及生命需求的临界时间范围。
被困人员需求主要包括心理需求、生理需求(或生活需求)及生命需求。国内外相关灾害救援研究表明,灾后4~8 h为应急启动阶段,这取决于外部救援力量的抵达时间[11];灾害发生12 h内,受灾人员基本生活得到有效救助[12];灾后24 h为营救黄金时间[13]。因此,结合相关灾害救援研究成果及具体隧道塌方事故的调查结果,确定24 h为生命需求时间点,12 h为生理需求时间点,6 h为心理需求时间点。
另外,为结合塌方实际情况确定需求时间,对2014—2020年间22例较大隧道塌方事故进行调研,调研结果显示:周边救援力量抵达时间在0~3 h内的事故救援占18.2%,抵达时间在3~6 h内的占63.6%,抵达时间超过6 h的占18.2%。由此可知,绝大部分的塌方事故,周边救援力量在6 h内均已抵达现场开展救援。
因此,综合最短需求时间点和塌方事故调研结果2方面,将6 h作为基本救援物资的需求时间。
1.3 应急响应时间确定
救援响应时间a0,指事故发生后信息传达延迟时间及应急车辆、人员及物资出发前准备时间之和。对2014—2020年间22例较大隧道塌方事故的救援响应时间进行调查,调研结果显示,救援响应时间在2 h内的事故救援占77.8%。由此可知,绝大部分塌方事故救援的响应时间在2 h内,因此将2 h作为应急响应时间上限。结合实际塌方事故调查情况,从不同救援车辆类型考虑,参照紧急医疗救援时间[14]确定救护车辆响应时间为0.5 h,考虑紧急程度、事故上报时间及大型救援设备拆卸装运时间确定重载及超限车辆响应时间为1.5 h,普通车辆按应急响应时间上限确定为2 h。
1.4 需求时间服务范围
将以受灾点为中心、需求时间(6 h)条件下最大资源运输时间为时间阻抗半径,绘制的不规则救援覆盖区域范围称为需求时间服务范围。步骤如下:
1)将需求点外6 h范围内资源作为重点,1级调度在该范围内进行。
2)若6 h需求时间服务范围内资源不能满足救援需求,则以1 h为递增值,逐级扩大范围寻找新供应点,并对物资供应路径制定应急管控预案。
3)因塌方初期无法准确估计事故的危害程度及救援难度,且塌方调研显示救援物资存在资源过剩,因此考虑资源需求量的不确定性。
2 基于需求时间服务范围的分级资源调度模型
假设A={Si|i=1,2,…,n}为供应点集合,以第j种应急资源为例,Φ为该种资源可选方案集合,Φ={Φs|s=1,2,…,n}。由于资源需求量的不确定性,拟采用模糊理论方法[15],用梯形模糊数表示受灾点的资源需求量,用α截集法做去模糊化处理,则受灾点对供应点Si第j种资源的需求量xij如式(3)~(5)所示:
(3)
L(α)=cij+(aij-cij)α
(4)
U(α)=dij-(dij-bij)α
(5)
式中:α为截集的阈值或水平,α∈[0,1],取0.5;cij,aij,bij,dij分别为需求点对第j种资源梯形模糊需求的阈值参数;L(α),U(α)为α截集的最小值和最大值;xij(α)为截集α的重心,这里指需求点对资源供应点的应急资源需求量。
2.1 模型基本假设
1)塌方救援调度网络由2种节点类型构成:受灾点和资源供应点。
2)隧道塌方事故只有1个受灾点,多个资源供应点参与物资调度。
3)需求点、资源供应点的地理位置已知。
2.2 引入需求时间约束的路径决策模型
为取得最优路径,从时效性、畅通可靠性角度出发,并引入需求时间约束,则路径选择决策的综合评价如式(6)所示:
(6)

(7)
(8)

(9)
λt+λk=1,0≤λt≤1且0≤λk≤1
(10)
式中:r为路径上路段数;Ka为路径上任意2节点间路段的畅通可靠度;p为畅通可靠度阈值;Q为道路路段车流量;C为道路通行能力。
式(7)为需求时间约束;式(8)为畅通可靠度阈值约束,本文以道路饱和度来评判畅通可靠度,当饱和度达到C级时道路出现堵塞现象,因此取阈值p为0.4;式(9)为任意2节点间路段畅通可靠度计算公式。
由于普通救援物资供应点多位于城市范围内,因此路段阻抗采用考虑非机动车辆的BPR修正模型[16];节点阻抗采用适用饱和度0~1.2复杂道路网的稳态延误公式。根据道路类型[17]对BPR函数待定系数进行标定;取节点阻抗参数c=80 s,λ=0.45,S=3 000辆/h(假定单进口道为2车道),x=0.8。
2.3 应急资源分级调度多目标优化模型
在最优路径确定基础上,考虑到救援对救援时间和调度物资数量的关注程度较高,提出救援效率概念,建立资源分级调度多目标优化模型。

(11)
(12)

式(11)为应急资源的调度成本最低,包括供应点的出动费用和运输物资成本;式(12)为调度方案的救援效率最高,用方案中参与调度的单个供应点在单位运输时间内调度的平均物资数量来体现。
英国心理学家理查德·怀斯曼对“正能量”有个定义:一切予人向上和希望、促使人不断追求、让生活变得圆满幸福的动力和感情。说得通俗点,就是一种积极向上、不断追求的精神意念、情感和动力。
(13)
(14)
0≤xij≤Xij,j=1,2,…,m
(15)

式(13)为应急资源的调度成本最低,包括供应点的出动费用和运输物资成本;式(14)为调度方案的救援效率最高,用方案中参与调度的单个供应点在单位运输时间内调度的平均物资数量来体现;式(15)为资源调度数量约束。
3 实例分析
以荣乌高速公路营尔岭隧道“9·30”坍塌事故为研究实例,以营尔岭隧道为假定塌方点,以河北省矢量路网图为数据基础,以ArcGIS软件为平台,借助“Network Analyst”工具箱服务区分析图层,求解需求时间服务范围。
3.1 实例概况
6 h需求时间服务范围内营尔岭隧道周围有10个应急物资中心(距离近的物资中心视为1个),包括蔚县、阜平县、易县、涞源县、唐县、涿州县、保定市、容城县、高阳县和霸州市(代号为S1~S10)。
以重载车辆为例,救援需要2类应急资源,分别为防护用品(Xi1)和排水机、发电机、通风机等抢险物资(Xi2)。考虑到塌方点的自救能力、地理条件、气候因素、受灾规模及以往不同救援规模的需求情况等,结合专家经验,设定本实例下资源的模糊需求量。设各资源供应点的储备量见表1,单位物资运输费用(bi1,bi2)及出动费用(ui)见表2。

表1 各资源供应点的储备量Table 1 Reserves of each resource supply point

表2 各资源供应点的单位物资运输费用及出动费用Table 2 Unit material transportation costs and dispatch costs of each resource supply point
通过梯形模糊数计算,得到需求点对2种资源的需求量分别为(1 050,70)。由表1可知,2种资源的储备总量分别为(1 600,60),说明第2类资源(Xi2)的储备总量不能满足需求,短缺的需求数量为10。因此,仅针对短缺物资Xi2,将服务范围从6 h扩大为7 h,则新增3个应急物资中心(代号为S11~S13),设Xi2的资源供应点储备量及费用见表3。

表3 资源供应点的储备量及费用Table 3 Reserves and costs of resource supply points
由表3可知,扩大服务范围后,应急物资均已满足需求,即可停止扩大服务范围。将分级需求时间服务范围合并到1个图,应急物资中心分布如图1所示,简化的道路网络如图2所示。
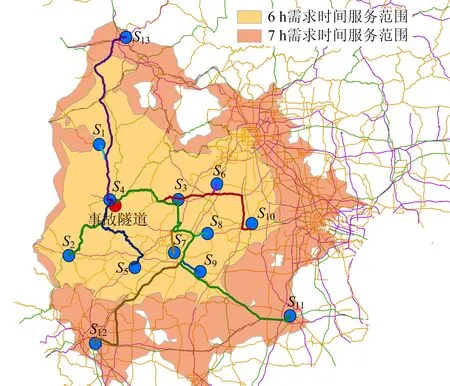
图1 应急物资中心分布Fig.1 Distribution of emergency material center

图2 简化的道路网络Fig.2 Simplified road network
3.2 最优路径求解
γj为第j种物资的换算系数,从重载车辆载重考虑,取1套防护用品净重约为6 kg,1台抢险救援设备净重平均约为60 kg,由此确定Xi1,Xi2换算系数分别为1,10。道路车流量Q,根据2017年河北省公路交通情况调查资料,获得具体道路的交通量数据。道路通行能力C,根据路段设计速度选取设计服务水平下对应的设计通行能力的规范值。假设决策者给出路径选择的时效性、畅通可靠性权重值为(0.5,0.5)。计算得到的最优路径见表4。

表4 资源供应点到需求点的最优路径Table 4 Optimal path from resource supply point to demand point
3.3 调度方案求解及结果分析
设计将TOPSIS法[18]引入NSGA-Ⅱ算法中,对分层调度模型求解并进行非劣解择优。在NSGA-Ⅱ基础上,分别假设救援效率最高、调度成本最小情况下目标模型的最优值、最劣值,计算非劣方案Φa与正负理想点的相对距离Ra,ra,最后计算方案对理想点的相对接近度εa。相对接近度值越大,方案越优,由此得到1组最优资源调度方案。相对接近度计算如式(16)所示:
(16)
式中:εa为非劣方案Φa对理想点的相对接近度;Ra为方案Φa与正理想点的相对距离;ra为方案Φa与负理想点的相对距离。
应用Matlab R2016a软件在Intel i7,CPU 2.3 GHz,RAM 8 GB服务器上进行编程计算,设置算法种群数为400,迭代次数为200,变异率为0.1,交叉率为0.7。考虑到不同救援阶段的救援需求不同,针对救援初期、救援中期和救援后期,调度成本权重和救援效率权重分别为(0.25,0.75),(0.5,0.5),(0.75,0.25)。
以6 h需求时间服务范围内救援初期为例,帕累托(pareto)前沿如图3所示(其他情况的pareto前沿趋势基本一致),算法运行时间为134.522 839 1 s。求解得到不同救援阶段的最优调度方案见表5。

表5 不同救援阶段的最优资源调度方案Table 5 Optimal resource scheduling schemes in different rescue stages

图3 双目标的帕累托前沿Fig.3 Pareto front of dual-objective
因为属于离散问题,自变量为整数,只有有限个解,因此pareto前沿不是1条完整的曲线。由pareto前沿分析目标函数的因变量f1,f2关系可知,在一定范围内(任一范围1~5),调度成本f1增加,救援效率f2随之显著提高;从总体趋势看,由范围1逐步变化到范围5,救援效率f2的提升亦伴随着调度成本f1的增加。由此可知,2者相互制约,符合实际情况。
对比6 h需求时间服务范围内不同救援阶段的最优调度方案可知,1级救援范围内的物资供应点需全部出动即S1~S10,救援初期最优方案的救援效率较中期、后期略高,分别提高6.1%,10.0%;但救援中期、后期的最优方案在救援成本上显著降低,较初期分别降低30.7%,40.6%。决策者可根据不同救援阶段实际需要选择适宜的调度方案,实现应急资源的调度。
由于资源总量不能满足第2类资源的需求,因此扩大服务范围至7 h,此时第2类资源的储备总量大于短缺需求量,已经满足需求,停止扩大服务范围。此时针对第2类资源的短缺物资量,2级调度计算得到最优方案均为:供应点S11调度5个单位,供应点S13调度5个单位。
3.4 制定应急交通管控预案
3.4.1 规划路径基本交通管控措施
从临时性应急交通角度出发,根据背景交通采取以下应急管控措施:1)根据紧急程度可采取单向绿波控制,将单向组织与应急车道相结合,确保一路畅通;2)可采取交通分流,对到达车辆进行劝返或改道,控制进入规划行驶路径的车流量;3)可采用临时性交通渠化,或进行左转交通组织,减少冲突点和延误;4)可临时限制大型车辆驶入;5)在交叉口组织人员指挥交通使其他车辆让行应急车辆,使应急车辆优先通过。
3.4.2 关键路段或交叉口具体交通管控措施
根据调查交通量数据显示,路网中25-24,37-25,39-38,21-12,58-56路段交通量较大,易出现交通拥挤。根据表4最优路径方案,25-24属于规划行驶路径,即一旦该路段拥堵,对救援时间影响最大,因此对该路段及周边交叉口进行应急交通管控。
将供应点出发到需求点的交通流向视为疏导方向(即节点25驶向节点24),节点25为涞涞高速与G234交叉的易县立交桥,为保障路段25-24畅通行驶,对节点25制定临时应急管控措施如下:
1)由于节点25为立交入口处,因此驶入车流量较大是造成路段25-24拥堵的主要因素之一,因此在立交入口处允许应急车辆优先驶入,并禁止特定车型如危险品车辆或大型客货车驶入,限制普通车辆驶入数量或暂时封闭入口通道,待拥堵状况缓解或拥堵车流消散后再恢复正常交通。
2)由于路段37-25与路段25-24同为拥挤路段,推测37-25路段继续直行车流量较大,是造成25-24路段拥挤的另一主要因素,因此在37-25高速路段及更远高速路段上,通过LED交通诱导屏发布前方拥挤路段交通信息,促使更多车辆在节点25处提前驶出高速,实现交通分流。
4 结论
1)提出需求时间概念,将需求时间服务范围分级调度与应急交通管控预案相结合,可充分满足应急物资的供应需求,有效保障救援时间,对应急资源调度方案制定及救援实施具有一定实用性。
2)考虑时效性和路径畅通可靠性,建立带需求时间约束和可靠度阈值约束的路径决策模型;针对救援时间和调度物资数量提出救援效率概念,建立调度成本最小、救援效率最高的双目标优化模型,在NSGA-Ⅱ算法基础上设计引入TOPSIS法求解最优调度方案。
3)相较于贯穿型塌方,空腔型塌方的围岩有一定自稳能力且有稳定空腔,有一定存活空间,存活几率较大,因此对空腔型隧道塌方的救援研究适用性更好。

