基于等维新息灰色马尔科夫的地铁客流量预测*
路 倩,王亚飞,杨 玲,白 鑫
(1.首都经济贸易大学 管理工程学院,北京 100070; 2.北京城市系统工程研究中心,北京 100035)
0 引言
目前,我国地铁建设已步入快速发展阶段,较多城市开通了地铁(包括轻轨)。据有关部门统计,2019年国内各大城市地铁建设总里程约4 600 km,是10 a前地铁建设里程的4倍[1]。因舒适性高、运载量大、速度快且受天气影响较小等优势,地铁成了城市轨道交通网络中发展最为迅速的交通方式[2]。越来越多的人们选择地铁作为出行工具,但有限的地铁车站和站内容量与日益增大的客流量相互矛盾,地铁人群拥挤并采取限时管制措施已成为地铁车站常态[3]。而且地铁车站通常设于地下空间,与其他交通工具所处的外部空间相比相对狭小,通道、安全出口的设置有限,如果发生突发事件极易发生拥挤与踩踏,甚至引起人群恐慌从而导致二次事故的形成[4]。因此对地铁客流量进行预测,掌握一定时期的客流数量和客流变化规律,对地铁站的运营管理及保障公共安全具有重要意义。
国内外学者对轨道交通客流预测已经进行大量研究,四阶段预测法、灰色模型、回归模型、SVM支持向量机等均为应用较广泛的预测方法[5]。Girish等[6]运用深度神经网络对地铁客流进行预测,得出性能优于传统的客流出行需求预测模型的结论;Roos等[7]通过改进期望最大化算法降维,学习动态贝叶斯参数和方法进行预测,预测效果令人满意,但面对突变客流时预测效果欠佳;Liu等[8]将改进优化粒子群算法与最小二乘支持向量机相结合,同时加入purning算法进行客流预测,得出此方法预测小样本非线性数据效果良好;叶红霞[9]引用非集计模型分析突发事件下乘客出行行为特征,建立突发事件情境下的客流分步预测算法;刘先超等[10]利用Eviews软件确定时间序列模型参数,建立较为理想的SARIMA模型,并以青岛3号线客流为基础进行验证;王茁等[11]引用BP神经网络模型对轨道交通日客流总量进行预测,预测计算精度达到87.3%,但仅适用于轨道交通开通初期的客流预测;仇建华等[12]以轨道交通突发客流量为研究对象,引用基于贝叶斯稀疏理论的相关向量机模型进行预测,得出模型经优化后其泛化能力更强,能够精准预测的结论。
关于地铁客流预测方面,国内外学者所取得的成果较丰富。但是,多数预测方法需要大量原始样本数据进行长时间的训练和优化处理,得出的结果才能令人满意,对于波动数据的预测能力普遍较弱。为解决此问题,本文提出等维新息灰色GM(1,1)模型与马尔科夫理论相结合的地铁客流组合预测模型,结合所需样本少和对波动大的数据精准预测2种特点,以期为相关单位了解地铁客流趋势和采取管控措施等提供参考。
1 组合预测模型的构建
1.1 灰色GM(1,1)建模过程
设X(0)为由n个数据组成的非负原始数据序列,X(0)={x(0)(1),x(0)(2),…,x(0)(k),…,x(0)(n)}。
在进行预测之前需要对数据序列进行检验处理,确定是否满足建立灰色预测模型的条件。通常用数列的级比σ(0)(k)(k=1,2,…,n)的大小与所属区间的对应程度来检验是否符合建模要求,如式(1)所示:
(1)
式中:n为数据个数。

1)对原始数列进行一阶累加生成,弱化数据的波动性和随机性,形成新的数据序列X(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}。其中x(1)(k)计算如式(2)所示:
(2)
式中:i为原始数据序列的位数;k为新数据数列的位数。
2)新生成序列近似服从指数规律,对其建立预测模型,如式(3)所示:
(3)
式中:a为模型的发展系数,反映X(1)以及X(0)的变化趋势;u为模型的灰作用量,反映数据之间的变化关系。
3)引入数据矩阵B,Yn,运用最小二乘估计一阶线性微分方程的待估参数a,u,如式(4)所示:
(4)

(5)
5)累减还原得式(6):
(6)
1.2 等维新息灰色GM(1,1)模型预测原理
等维新息灰色GM(1,1)模型是将原始数据序列经过灰色预测得到1个预测值x(0)(n+1),将得到的预测值加入原始数据序列最后,摘除原始数据序列的第1个数值x(0)(1),总体保持数据序列{x(0)(2),x(0)(3),…,x(0)(n+1)}的数据个数不变,运用组成的新数据序列进行GM(1,1)模型,得出预测值的下一个值。如此不断地加入新数据,删除旧数据,直到完成预测目标为止[13]。等维新息灰色预测模型流程如图1所示。

图1 预测流程Fig.1 Prediction flow chart
一般来说,在等维新息灰色GM(1,1)预测模型中,原始数据序列的数据个数不能少于4[14]。在实际建模过程中,也需要考量模型的精度和实现效果来确定原始数据的使用个数,并非所有的原始数据均使用效果最好。
1.3 模型精度检验
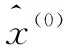
1)后验差比值检验
残差序列如式(7)所示:
(7)
残差序列均值计算如式(8)所示:
(8)
相对误差计算如式(9)所示:
(9)
平均相对误差计算如式(10)所示:
(10)
方差比计算如式(11)所示:
(11)
2)小概率误差检验
小概率误差计算如式(12)所示:
(12)
一般情况下,将模型精度划分为4个等级,具体各指标见表1[15],表1中3个精度指标若有1个不满足当前精度等级即视为预测精度未达到当前等级。

表1 模型精度等级划分Table 1 Classification of model accuracy
1.4 马尔科夫模型修正过程
当建立的模型精度经检验不合格时,需要考虑对原模型进行修正,从而提高预测精度。马尔科夫模型根据状态之间的转移概率描述过程的变化状态[16]。模型步骤如下:
1)状态划分
根据马尔科夫链,按照等概率原则将数据序列分成若干状态,任一状态区间可表示为:Em∈[E1m,E2m],其中,E1m和E2m为状态E的上下限。状态划分数量与实际值和预测值的相对误差范围以及样本的数量有较大关系。为提高对波动数据修正的有效性,并提高客流预测精度,本文将状态划分为3个。
2)计算概率,确定状态转移矩阵
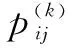
(13)

状态概率组成的k步状态转移矩阵如式(14)所示:
(14)
式中:R(k)为由状态概率组成的k步状态转移矩阵。
若V(0)为初始状态Ei的初始向量,则经过k步转移之后,状态向量V(k)如式(15)所示:
V(k)=V(0)×R(k)
(15)
在实际应用中,一般只需考察1步转移概率矩阵R。
3)计算预测值
马尔科夫运行过程无后效性,假设预测对象处于Ek状态(k=1,2,…,m),则只需了解状态转移矩阵第k行的概率即可,如果在某一行中第i列的转移概率值最大,那么可以认为下一时刻预测对象由Ek状态转向Ei状态的可能性最大[17]。当矩阵中第k行有2个或者2个以上概率相同时,如果第k行为第1行或最后1行,则取靠两边的列;如果为中间行,则取靠中间的列[18]。
4)计算修正后的预测值
预测对象下一步所处状态Ej,其区间值为[E1j,E2j],则通过模型预测值的修正公式如式(16)所示:
(16)
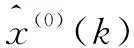
2 实例分析
本文以北京轨道线网日均客运量为研究对象,选取2009—2018年全网日均客流量作为原始数据序列,数据见表2。

表2 2009—2018年北京轨道线网日均客运量分布Table 2 Distribution of average daily passenger flow in Beijing rail transit network from 2009 to 2018
2.1 北京地铁客流量灰色GM(1,1)预测
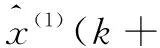
2.2 客流量等维新息灰色GM(1,1)预测

灰色GM(1,1)模型和等维新息灰色GM(1,1)模型的预测结果见表3。

表3 灰色GM(1,1)模型和等维新息灰色GM(1,1)模型的预测结果Table 3 Prediction results of grey GM(1,1) model and equal dimension and new information grey GM(1,1) model 万人·次
以上2种预测模型精度对比结果见表4。
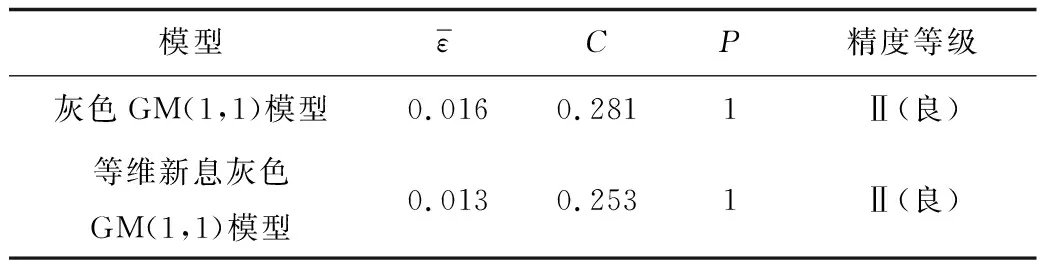
表4 2种模型的预测精度对比Table 4 Comparison on prediction accuracies of two models

2.3 预测结果马尔可夫模型修正
将由等维新息灰色GM(1,1)预测的获取相对误差值划分为3种状态,分别记为E1=(0.14%,2.17%),E2=(-1.90%,0.14%),E3=(-3.43%,-1.90%)。从以上状态分类中可获得2013—2018年统计范围的状态转移情况,见表5。
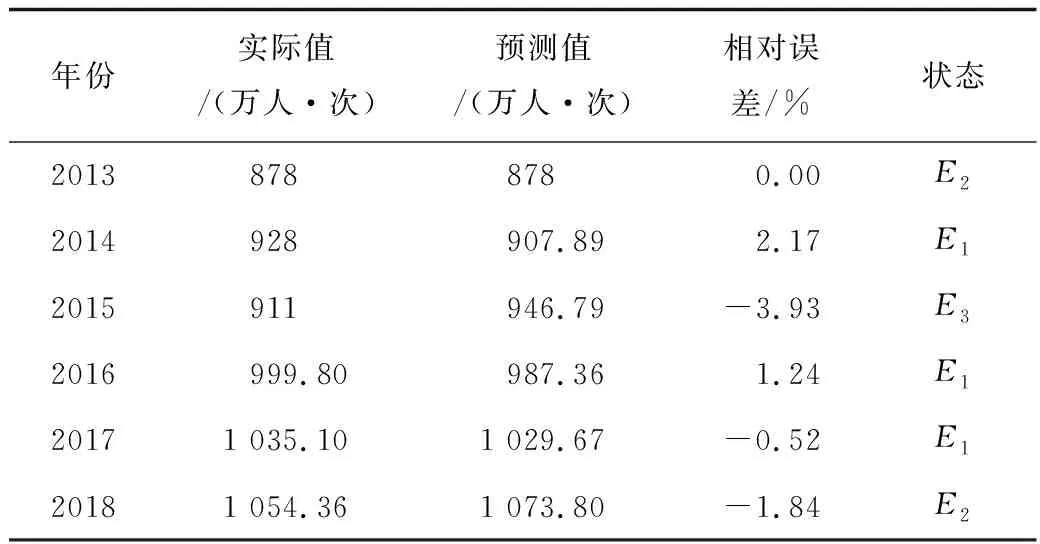
表5 状态划分情况Table 5 Status division
由表5可知,E1共出现了3次,E2共出现了2次,E3共出现了1次。根据式(13)~(14),1步转移矩阵根据原始状态样本数和转移的样本数的比值为:
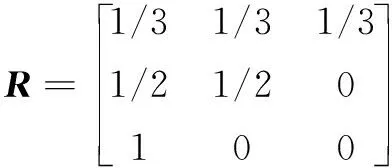
多步状态转移矩阵R(k)=(R)k。
当预测值相对误差较小时,不需要利用马尔科夫模型修正(一般小于1%),故2013年、2017年的预测值不需要修正。以2014年的预测值修正为例,计算经过灰色等维新息马尔科夫模型修正后的预测值,2014年度的预测误差处于状态E1,按照上述状态转移概率,下一步状态转移位置为E3,则根据式(16),修正后的预测值为:
同理,其他年份的预测值,可用马尔科夫修正其他年份的客流量预测值,修正结果见表6。
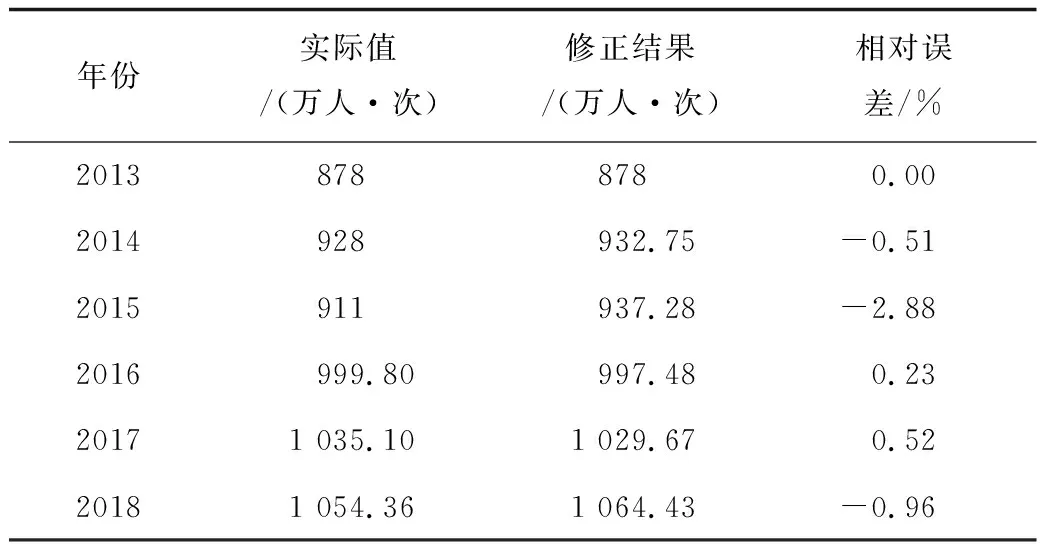
表6 马尔科夫修正结果Table 6 Results of Markov correction
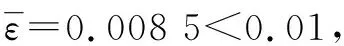

图2 3种模型预测结果曲线Fig.2 Curves for prediction results of three models
3种模型的相对误差对比图如图3所示。其中,ε1为灰色GM(1,1)模型进行预测后与原始数据的相对误差;ε2为等维新息灰色GM(1,1)模型进行预测后与原始数据的相对误差;ε3为等维新息灰色马尔科夫模型预测后与原始数据的相对误差。对比3种模型的相对误差,整体来看等维新息灰色马尔科夫模型表现更好,误差更小。
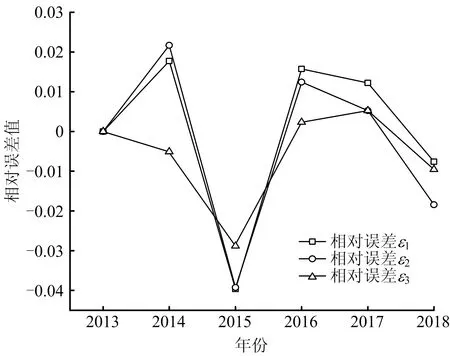
图3 3种模型相对误差值对比Fig.3 Comparison on relative error values of three models
运用等维新息灰色GM(1,1)模型对2019—2021年3 a北京地铁的全网日均客运量进行预测。首先预测2019年北京地铁的全网日均客运量,根据马尔科夫模型的预测经验,选择距预测年份最近的3 a作为预测基础年份,根据各年份的状态及转移步数,得到北京地铁的全网日均客运量的累积转移概率见表7,2016年、2017年和2018年3 a向2019年转变的状态转移概率相加,得到的最大数值是1.56%,处在E1(0.14%,2.17%)的范围内,所以未来1 a最有可能存在于状态E1。根据同样的方法计算未来2,3 a的状态转移概率,从而得出当年的客流量值。

表7 2019年北京地铁的全网日均客运量状态预测Table 7 Prediction on status of average daily passenger flow in whole network of Beijing Subway in 2019


表8 2019—2021年全网日均客运量预测值Table 8 Prediction values of average daily passenger flow in whole network from 2019 to 2021 万人·次
由北京市轨道交通指挥中心提供的数据可知2019年日均客运量为1 085.58万人次,可以看出等维新息灰色马尔科夫预测值与实际值更为接近,正常情况下未来北京地铁的全网日均客运量仍然会呈现逐年增长的态势,可以根据预测值来采取管控措施或进行资源设备的合理配置,使地铁利用率实现最大化。
3 结论
1)为精准预测地铁客流量,了解地铁客流的变化趋势,采用等维新息灰色马尔科夫模型,对比灰色GM(1,1)、等维新息灰色GM(1,1)2种模型,相对误差值、后验差比值和小概率误差精度的表现均有提高,可以看出等维新息灰色马尔科夫预测模型在地铁客流量预测方面表现优越,对比其他2种方法,预测精度表现为Ⅰ级(优)。
2)提出的模型结合使用样本数量少的灰色模型和处理波动数据序列能力优异的马尔科夫模型2种模型的特点,运用小样本预测地铁全网日均客运量,预测精度更高,预测曲线具有波动性,更加符合我国历年来全网日均客运量的变化特点。
3)运用新模型预测3 a的客运量,发现未来的客运量趋势仍持续走高,需要提前采取管控措施应对未来的客流增长趋势,以便保障乘客通行安全和地铁高效运营。
4)等维新息灰色马尔科夫模型的预测精度相对其他2种模型预测精度更高,但波动较大的时间节点仍存在较大误差,下一步将考虑对这些误差较大的时间节点预测值进行再处理,以达到更加精准的效果。

