基于双层规划的危险品运输专用车道优化设计
张圣忠,余永骎
(1.长安大学 经济与管理学院,陕西 西安 710064; 2.长安大学 运输工程学院,陕西 西安 710064)
0 引言
道路运输是危险品运输的主要方式,我国危险品道路运输量占危险品运输总量的70%。危险品运输事故一旦发生,后果严重,故如何降低道路运输风险受到学术界的广泛关注。危振等[1]结合危险品货物运输路线选择的特点,建立以最小运输成本和最小运输风险的双目标路径优化模型;项寅等[2]将公路旁的人口聚集场所定义为“脆弱点”,以最大化危险品车辆运输路径和脆弱点之间的最小加权距离为目标构建双层模型;Du等[3]开发1种模糊双层规划模型,用于降低在多个仓库对客户交付危险品时的总体运输风险。但是现有研究在考虑危险品运输风险时,多假定路段事故概率一致,忽略危险品运输车辆和小汽车混行对事故概率的影响。
危险品运输车辆和小汽车混行存在一定的风险,这是因为危险品运输车辆行驶时有速度的限制,如在普通公路上限速60 km/h,在高速公路上限速80 km/h,此种速度限制会造成危险品运输车辆和小汽车之间存在一定的速度差,使小汽车的超车换道次数增加[4],导致小汽车和危险品运输车辆碰撞概率增加。有研究指出速度差和事故之间的关系曲线接近U型,意味着较大的速度差会导致发生事故的概率增大[5]。很多学者开始考虑将货运和其他交通流进行分割,以提高货运的安全性。通过仿真模型的研究,货运专用道的设立可以减少车辆的换道行为,减少追尾和超车换道冲突,提升驾驶安全性[5-7]。在实践中,也有地区已经规划危险品专用车道,如天津市的滨海新区和山东省东营市,均取得良好的效果。因此研究危险品专用车道的布置可以提升危险品运输的安全性,具有一定的现实意义。
虽目前已有学者对危险品专用道问题进行研究[8-10],但现有研究均是将危险品专用道问题视为双目标问题,多以风险最低和对正常交通干扰最小为目标构建模型,忽略了规划者和出行者之间的主从博弈关系。此外现有研究多通过衡量相邻车道通行时间的增加值来研究专用道的布设对正常交通的影响,但专用道的布设会导致路网整体通行状况的改变,进而影响出行者的出行决策。因此需要从路网的角度出发,研究规划者、危险品运输车辆、小汽车之间的相互关系。因此,本文从路网的角度出发,基于双层规划对危险品专用车道的布局方案进行研究。
1 危险品运输专用车道布局模型
1.1 问题描述
危险品运输专用车道的布局问题是1个多方参与的决策问题,规划者考虑的是路网整体的安全性和运行效益,而出行者考虑的是自身出行成本。此问题符合Stackelberg博弈,即规划者优先做出决策,出行者根据规划者的决策进行出行路径的选择。因此,本文构建危险品运输专用车道的多目标双层规划模型。
1.2 模型假设
本文模型作出以下假设:
1)路网中只存在2种车辆类型,即小汽车和危险品运输车辆;
2)路网中的OD量(起讫点的交通出行量)已知;
3)路网中的每个路段有2个车道;
4)当路段中存在专用车道时,危险品运输车辆必须在专用车道上行驶;
5)每个路段上的危险品运输事故是独立发生的。
1.3 模型建立
1)上层模型
上层规划模型具体描述规划者的3个目标为:1)以最大化社会效益为目标,即保证所有车辆的通行总体出行成本最小(用阻抗和交通量的乘积衡量);2)以社会安全风险最小为目标,即保证危险品车辆运输风险最低;3)以专用道整体利用率最高为目标。模型如式(1)~(4)所示:
(1)
(2)
(3)
s.t.
nh/na≤σ
(4)
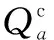
目标函数式(1)表示最小化所有车辆总体出行成本;目标函数式(2)表示最小化危险品运输风险;目标函数式(3)表示最大化专用道整体利用率;约束条件式(4)表示危险品运输专用道占总路段的比例不超过σ。
2)下层模型
下层模型包含2个子模型,危险品运输车辆流量分配模型和小汽车流量分配模型。
①危险品运输车辆流量分配模型
危险品运输车辆会选择路网中阻抗最小的路径,符合用户均衡原则。当实现均衡状态时,所有危险品运输车辆的总体出行成本最小。模型如式(5)~(8)所示:
(5)
s.t.
(6)
(7)
(8)
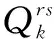
约束条件式(6)表示路径总流量等于OD总量;约束条件式(7)表示路段a流量等于经过路段a的所有路径流量相加;约束条件式(8)表示路径流量不为负值。
②小汽车流量分配模型
小汽车流量分配模型如式(9)~(12)所示:
(9)
s.t.
(10)
(11)
(12)

约束条件式(10)表示路径总流量等于OD总量;约束条件式(11)表示路段a流量等于经过路段a的所有路径流量之和;约束条件式(12)表示路径流量不为负值。
3)阻抗函数设定
路段阻抗函数描述路段上流量和费用之间的关系,常用的阻抗函数是美国联邦公路局函数,即BPR函数,如式(13)所示:
(13)

①混行条件下
根据文献[12]可知,在考虑小汽车和大型货车混行的条件下,当大型货车的百分比低于60%时,交通混行对车辆的影响很小,可以使用标准的BPR函数。本文考虑到实际中危险品运输车辆占比较小,因此可直接使用BPR函数。在混行条件下的阻抗函数如式(14)所示:
(14)
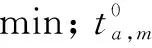
②非混行条件下
在非混行情况下,小汽车和危险品运输车辆在各自的车道行驶,互不干扰,因此直接使用BPR函数衡量阻抗,小汽车的阻抗函数如式(15)所示:
(15)
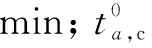
考虑到危险品运输存在某些路段限行的限制,使用变量μa衡量危险品车辆的限行情况,若路段a限行,则μa为非常大的实数,否则μa=1。
危险品运输车辆的阻抗函数如式(16)所示:
(16)
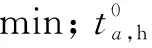
4)风险评估
传统的危险品运输风险评价模型如式(17)所示:
(17)
式中:Ea为路段a周边暴露的人口数;Pa为路段a发生事故的概率。但是传统的风险评价模型忽略了速度差和交通量的变化对事故概率的影响。
有学者指出路段交通流的增加会减少车辆间的安全间距,导致发生事故的概率增加[13]。而张芝等[14]通过仿真实验得出车辆超车和追尾行为与交通速度流标准差成正比,在一定范围内也与交通流量成正比。本文参考文献[14],用占位冲突次数代替事故概率,衡量路段的风险值。衡量占位冲突次数的模型如式(18)所示:
(18)
式中:Na为路段a的占位冲突次数;σa为路段a含有危险品车辆的交通流速度的标准差;t为单位时间,h;La为路段a的长度,km。路网的风险评估模型R如式(19)所示:
(19)
2 模型算法设计
本文使用NSGA-2算法求解双层规划模型,求解步骤如下:
1)初始化
①确定染色体的编码方案。每个染色体采用实数编码,对应1组01决策变量,表示1种专用道的布局方案。
②设置相关参数,包括种群规模、迭代次数、交叉概率、变异概率。
③限制染色体中设置专用道的路段比例不超过σ,生成满足要求的初始种群。
2)计算初始种群中的适应度并对种群进行排序
①将染色体表示的专用道布局方案代入到下层流量分配模型中,使用FrankWolfe算法进行交通流分配,得到各路段流量和通行时间。
②根据各路段流量和通行时间计算上层目标函数值,计算的结果即为染色体的适应度,并将适应度添加到染色体矩阵中。
③使用非支配排序对种群进行排序,将计算得到的排序值和拥挤距离添加到染色体矩阵中。
3)竞标赛选择
根据二元竞标赛方法,选取适应度高的个体进入下一代。
4)交叉变异
根据设定的交叉概率、变异概率,采用模拟二进制交叉和多项式变异对种群的个体进行交叉变异,产生新的子代种群。
5)合并父代和子代种群,对合并后的种群进行非支配排序,选取优先子代组成新的种群。
6)判断种群进化是否达到最大迭代次数,若是,则算法结束,输出种群,否则执行3)。
3 算例分析
3.1 算例网络
本文使用1个包含12个节点、32个路段的算例网络对算法进行测试。算例网络如图1所示,其中,设定节点3-7和节点7-3路段对危险品运输车辆限行。

图1 算例网络Fig.1 Example network
危险品运输车辆OD交通量、路段对应距离和通行能力见表1~2。根据美国交通研究委员会(TRB)出版的《道路通行能力手册》,单辆货车的PCU值在1.25~2之间[15]。本文设定单辆危险品运输车辆的PCU值为2。
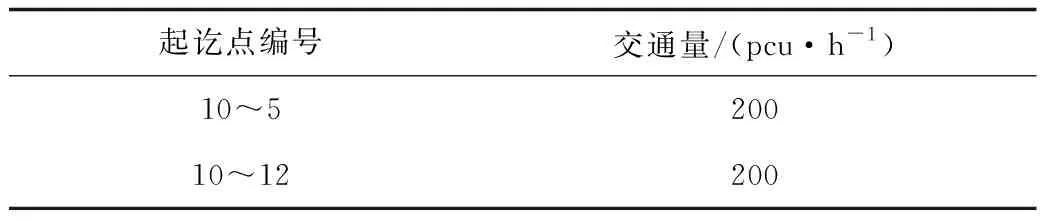
表1 危险品运输车辆OD交通量Table 1 OD traffic flow of dangerous goods transportation vehicles

表2 路段长度和通行能力Table 2 Lengths and passing capacities of road sections
3.2 算例结果分析
采用本文的算法在Matlab2018b软件上对模型进行求解,在主频为1.6 GHz的IntelCorei5处理器、操作系统为Win10的环境下进行。算法的部分参数设置如下:种群大小为60,迭代次数为80,交叉概率为0.9,变异概率为0.1,阻抗函数中α=0.15,β=4,危险品运输专用道占总路段的比例θ不超过0.2。
求解模型得到的目标值和对应的专用道设置方案见表3。
由表3可知,通过模型求得的专用道方案能取得1个较好的风险控制效果,降低由于车辆混行带来的风险。决策者需要考虑对不同目标的偏向,选择对应的方案。当决策者偏向更低的时间成本时,选择方案2;当决策者偏向更好的风险控制效果和专用道整体利用率时,选择方案1。

表3 求解模型得到的专用道方案Table 3 Reserved lane scheme obtained by solving model
3.3 相关因素对专用道设置效果影响分析
危险品运输车辆OD交通量变化和是否采用路径限制政策对专用道设置效果会有不同程度的影响,本文在方案1的基础上对这些影响因素进行分析。
1)危险品运输车辆OD交通量的影响
不同危险品运输车辆OD交通量下的专用道设置效果如图2所示,由图2可知,随着危险品运输车辆OD交通量的增加,设置专用道对正常交通的影响逐步下降,风险降低率和专用道整体利用率则在逐步上升。表明危险品运输专用车道在危险品运输车辆OD交通量较大的情况下能取得更好的效果。

图2 危险品运输车辆OD交通量对专用道效果的影响Fig.2 Influence of OD traffic flow of dangerous goods transportation vehicles on effect of reserved lane
2)路径限制政策的影响
路径限制政策指监管部门通过相关政策限制危险品运输车辆必须选择含有专用道的路径进行运输。在不同危险品运输车辆OD交通量下采用路径限制政策后的专用道方案改善效果如图3所示。由图3可知,采用路径限制政策后,专用道的风险控制效果和专用道整体利用率相比于原方案取得较大的改善,风险控制效果改善比大于90%,专用道整体利用率改善比约50%。时间控制改善比较小,但随着危险品运输车辆OD交通量的增加,采用路径限制政策后时间控制改善效果越来越明显。表明在危险品运输车辆OD交通量较大的情况下,采用路径限制政策对正常交通的干扰更小。

图3 路径限制政策对专用道效果的影响Fig.3 Influence of route restriction policy on effect of reserved lane
4 结论
1)从路网的总体角度出发,提出1个以总体出行成本最小、路网风险最小、专用道整体利用率最高为目标的双层规划模型。基于NSGA-2算法设计双层规划模型的求解算法,并结合算例网络对该方法进行应用。结果表明,该模型可以在限制专用道数量的前提下,实现较好的风险控制效果和较低的总体出行成本。
2)通过对影响专用道设置效果的因素进行分析,表明在危险品运输车辆OD交通量较大的情况下,设置专用道能取得更好的效果。
3)对危险品运输车辆采取路径限制政策,可以极大地改善专用道的风险控制效果和专用道整体利用率,在实际应用中可以考虑将路径限制政策和危险品专用道布局方案相结合,以取得更好的效果。

