椭圆内接菱形的性质——一道模考试题的研究

安徽省濉溪县第二中学(235100) 张瑞禹 祝峰

菱形和椭圆都是中心对称图形.菱形内接于椭圆时,会呈现出丰富的性质.下文以一道模拟试题为起点,探讨这些性质.旨在深化对这类问题认识,为教学、命题提供借鉴.

一、问题展示

(I)求Γ 的方程;

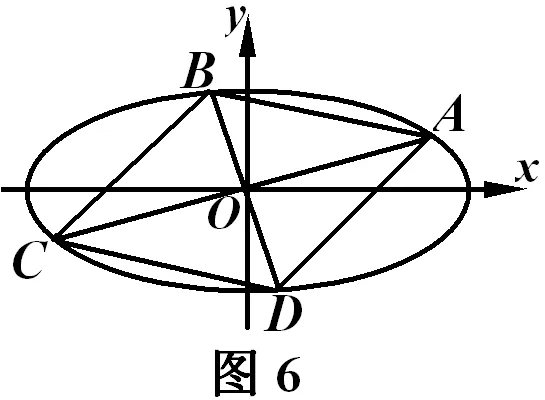
(Ⅱ)如图1,若菱形ABCD 内接于椭圆Γ,求菱形ABCD 面积的最小值.

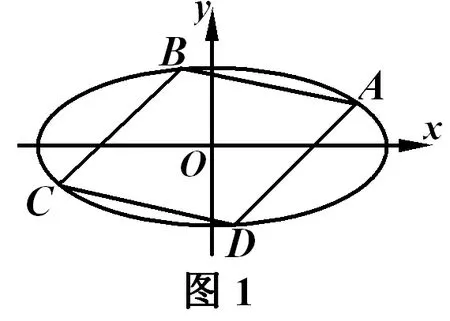
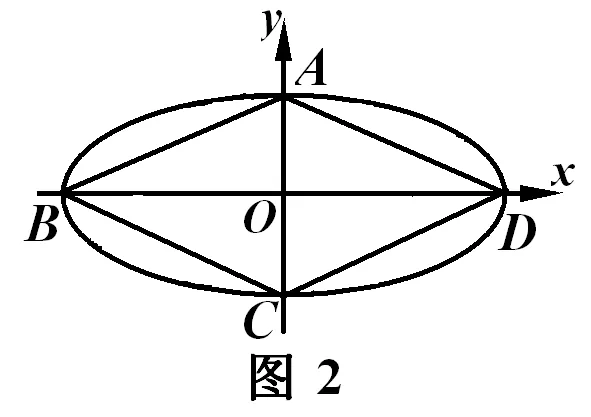
二、对称中心重合可以默认吗?

综上命题成立,可得下述定理.

定理1椭圆与其内接菱形中心重合.

上述论证过程,稍显冗长,却是证明这一问题的通法.如果能证明椭圆两平行弦的中点连线过椭圆中心,也能证明此定理,行文关系,在此不予赘述.

解题过程,不应轻言“易知”,该想清楚的地方,丝毫不能含糊.按着别人(包括文本)的指引学习和思考问题,无法真正学会思考、学会学习.感觉并发现结论是数学学习重要步骤,但数学相信理性、尊重事实,崇尚谨慎判断、公正评价、敏于探究、追求真理的批判性思维,不能用感觉来代替清晰的思维过程及严密的逻辑判断.

三、内接菱形面积最小值的求法举隅及一般性结论

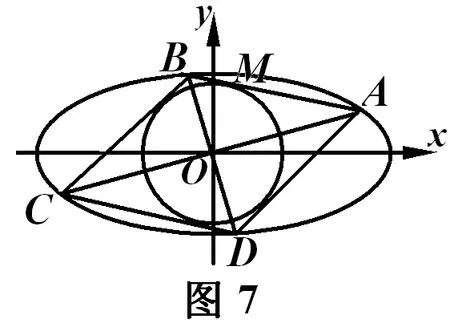
1 求法举隅

2 一般性结论

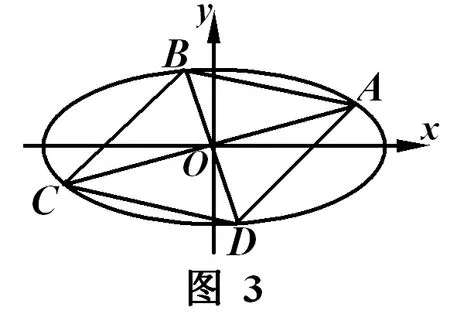
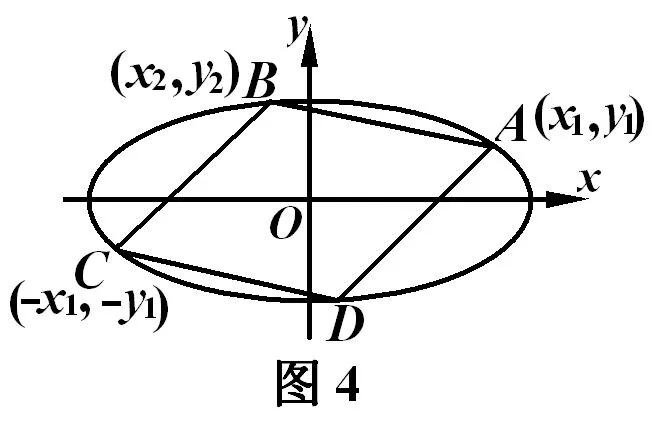
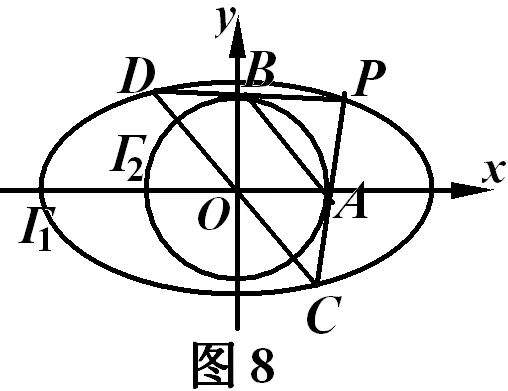
四、椭圆内接菱形的其它性质

菱形面积最小.

五、结语

试题的求解过程中,巩固知识、提升能力应该是第二位的.重要的是通过解题学会数学地思维,即逐步学会更清晰、更深入、更全面、更合理的进行思考,努力提升思维的整体性与灵活性、自觉性与创造性,实现对日常经验与直观感知的必要超越.

思维的清晰性和合理性方面,探究过程中,两图形中心重合问题,没有人云亦云,而是在严密地推理后才下结论.思维的深入性方面,面积最小值的求解没有满足于解答问题,而是从不同角度考虑,从不同思维方法中优化思维的灵活性.

思维的全面性方面,对于内接菱形,没有仅局限于问题设置中面积最小值的求解,而是更一般地考虑内接菱形的性质,积累全面思考问题的习惯,逐步提升思维的合理性.

整体性思维而言,可作更一般的考虑,椭圆的内接平行四边形会怎样? 可以考虑诸如以下问题:(1)平行四边形内接于椭圆的充要条件是它们的对称中心重合吗? (2)如何求椭圆内接平行四边形面积、周长的最值? (3)椭圆存在四边所在直线都有斜率的内接矩形吗? 当然,也可以由内接类比到外切,即椭圆的外切平行四边形会有什么性质?

“发展学生数学核心素养”的思想启示下,数学的解题应超越具体的知识和技能,深入到思维层面,由具体的数学方法和策略过度一般性的思维策略.帮助学生由“学会数学地思维”转向“学会思维”,不断提升自身思维品质,才能实现素养目标的达成.