数形结合中不可忽视的“隐患”

广东省中山市中山纪念中学(528454) 李文东

数形结合是重要的数学思想方法之一,我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微”.在解决函数问题时,我们经常会采用数形结合的思想和方法,通过数与形之间的对应与转化来解决函数问题,使得复杂的问题简单化,抽象的问题直观化.由于我们在数形结合时,作出的一般只是函数的大致图像,但是有些时候需要我们对函数的细节把握的更清楚,这些细节是数学结合中的“隐患”,作图时如果不消除这些“隐患”,往往就会导致严重的错误.本文就数形结合中常见的一些“隐患”举例说明,以期将这些“隐患”消除在萌芽中!

一、由定义域导致的“隐患”

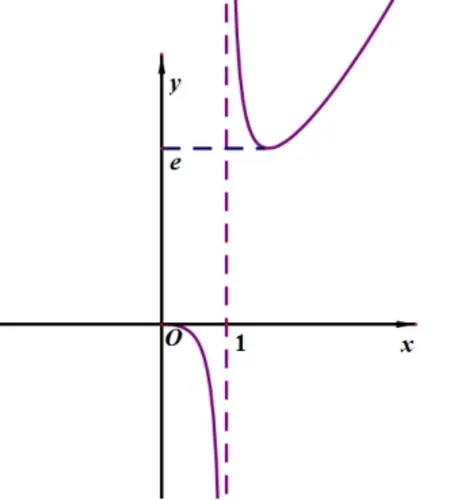
图1

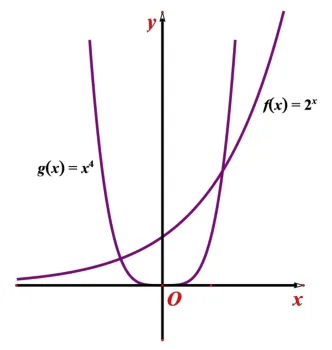
图2

二、由增长速度导致的“隐患”

例2函数h(x)=2x-x4的零点的个数为____.

解函数h(x)=2x- x4的零点的个数⇔方程2x-x4=0 的解的个数⇔函数f(x)=2x与函数g(x)=x4图像交点的个数.在同一坐标系中作出这两个函数的图像(如图2),容易看出这两个函数图像有两个交点.由于f(x)=2x和g(x)=x4在(0,+∞)上都为增函数,且随着x的变大,函数f(x)=2x的增长速度会远远超过g(x)=x4的增长速度,又h(2)＜0,h(20)=220-204=324-204＞0,故在(2,20)内两函数图像还会有一个交点.综上函数h(x)零点的个数为3 个.

评注因为函数f(x)=2x与函数g(x)=x4增长速度都比较快,数形结合很难直观完整的反映出两者图像直接的关系,作图时若不考虑到它们之间的增长差异性,则会得出两个零点的错误结论!

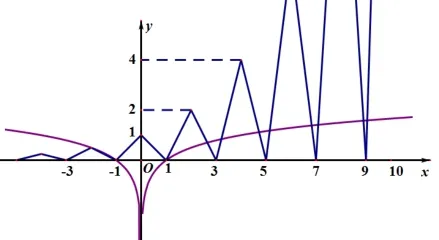
图3

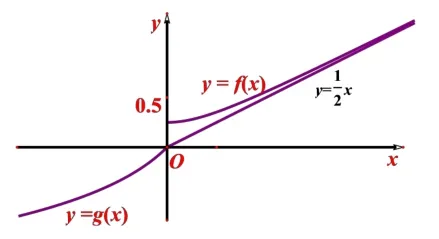
图4

三、由渐近线导致的“隐患”

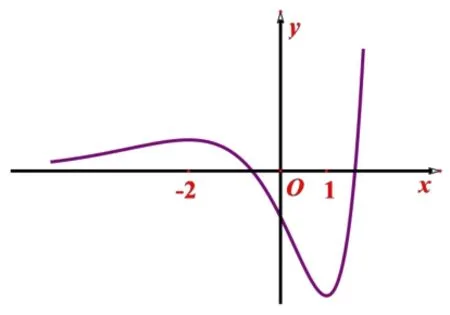
图5

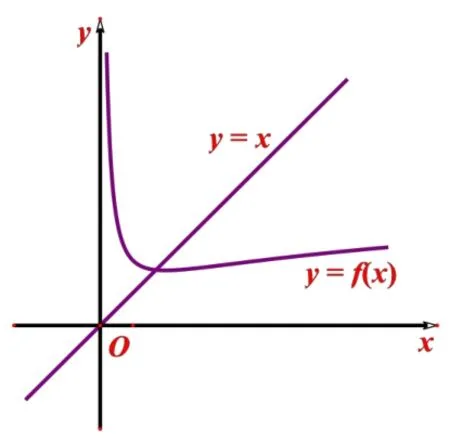
图6

四、由凹凸性导致的“隐患”

评注本题若没有考虑到f(x)在(2,+∞)上的凹凸性,则有可能得出2 个零点的错误结论!

五、由特殊点导致的“隐患”

例7(2015年高考山东卷)设函数f(x)=ln(x+1)+a(x2-x),其中a ∈R.

(1)讨论函数f(x)极值点的个数,并说明理由;

(2)若∀x＞0,f(x)≥0 成立,求a 的取值范围.

评注本题是山东省高考的压轴题,原题解法是采用分类讨论,比较复杂,这里我们采用分离函数,数形结合的方法,显得直观简便,当然其中除了要考虑函数图像的渐近线和增长速度外,还特别需要注意函数g(x)在x →0 时的函数值的情况,否则会得出a 的取值范围为[0,+∞)错误的结果!

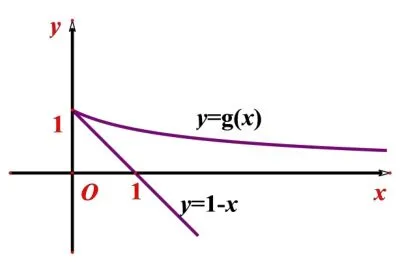
图7

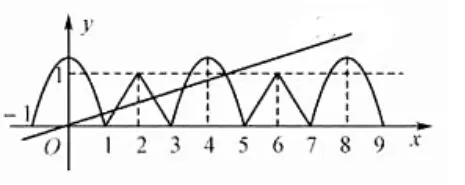
图8

六、由直觉导致的“隐患”

评注在采用数形结合时,对于一些涉及函数图像细节的地方,我们不能过于依赖直觉,有时还需要用数(计算)来辅助解决!

一般来说,在函数作图中,我们需要考虑:

1 确定函数的定义域;

2 判断函数是否具有奇偶性,周期性及其它的对称性,方便快速作图;

3 确定函数的增减区间和极值点;

4 确定函数的凹凸性和拐点;

5 确定函数是否具有渐近线;

6 求出一些特殊点的函数值;

7 多个函数之间有时还需要比较增长的速度.

只要我们做到以上这些,就能防患于未然,真正完美的发挥数形结合的功能!