基于符号回归算法的地铁盾构刀盘扭矩预测研究*
尹志清 翟维骏 韩爱民 陈 冬 郝保安 李 彤 陈 冲
(1.中交隧道工程局有限公司,100102,北京;2.南京工业大学交通运输工程学院,210009,南京;3.江苏省地质矿产局第一地质大队,210041,南京;4.南京坤拓土木工程科技有限公司,210041,南京;5.江苏省隧道与地下工程技术研究中心,210041,南京∥第一作者,高级工程师)
刀盘扭矩是地铁盾构机掘进的重要参数,是判定盾构刀盘及主轴工作状态的关键指标。目前,地铁盾构隧道施工中刀盘扭矩的施工参考值往往由施工单位通过既有经验推测,并经组织会议确定,故存在人为不确定性且时间成本较大;当面对掌子面地层组成复杂的复合型地层时,取值过于保守会导致掘进速率过慢,而扭矩初定值过大则会导致刀具过量磨损,从而增加了开仓换刀的经济、时间成本。所以,根据地层条件准确预测盾构刀盘扭矩可以有效指导盾构施工,降低施工成本,并提高施工效率。
刀盘扭矩的关键影响因素和各因素对扭矩的影响程度对指导施工有重要的意义,国内外的研究者为此也取得了一定的成果[1-5]。通过对φ1 800 mm盾构机模拟试验,对刀盘切削土体进行理论分析,得到了高精度的扭矩模拟数学模型[6]。通过对影响盾构刀盘扭矩的不同因素进行量化分析,建立了一系列较高精度的盾构刀盘扭矩预测模型[7-8]。依托于非线性支持向量回归和神经网络算法,得到了盾构扭矩预测的方法[9-10]。这些方法精度较高且得到了不同围岩条件下各因素对扭矩的影响程度。但是,目前使用物理分析建立盾构刀盘扭矩预测的模型,大多依赖于测定的地层参数,只能适用于特定工程且难以对扭矩进行实时预测。通过神经网络建立盾构刀盘扭矩预测的模型,大多因训练集较小导致模型不能精确地反映全局的最优解[5,11]。
刀盘扭矩的理论预测法同样存在局限性。工程勘察的精度难以满足复杂地层条件下精确建模的需要,地层参数与盾构掘进过程中各项参数的相互影响,难以通过受力分析得到精确、真实的表达式来真实地描述刀盘扭矩与各影响因素间的物理关系。但是,地层的性质以及地层与盾构间的相互关系反映在掘进中推力、贯入度和土仓压力等掘进参数中,并且推力、贯入度和土仓压力可以实时、准确地得到。此时符号回归(Symbolic Regression)算法作为一种数据驱动模型,可以很好地规避这一问题。
符号回归算法是基于遗传算法(Genetic Algorithm)的一种回归方法,与线性回归、逻辑回归等数值回归相比,符号回归不需要提前假设各变量所服从的函数形式,适用于处理热力学[13]、工程控制学[14]、地质及采矿工程、算法改良、虚拟系统优化、电子电路设计[15]等物理关系复杂、物理方程难以确定的非线性问题。本文依托深圳地铁8 号线深外站—盐田站区间盾构掘进复合地层的工程实践,运用符号回归算法建立预测刀盘扭矩的通式,在变量关系未知的情况下采用符号回归算法对目标物理量进行预测,并分析各变量以及刀具更换对刀盘扭矩的影响。相关成果精度较高且方便应用,丰富了盾构掘进复合地层的参数控制技术。
1 工程概况
深圳地铁8 号线深外站-盐田站区间原始地貌为低丘陵,现为居民区及道路,其两侧市政管线较为复杂。场地上覆Q4ml 素填土、填砂、填碎石等,下伏微风化中细粒花岗岩,工程地质条件复杂。选取该区间工程右线250 环至330 环的掘进数据进行分析(地质情况如图1),隧道主要穿越微风化中细粒花岗岩、中等风化中细粒花岗岩。其地层性质见表1。
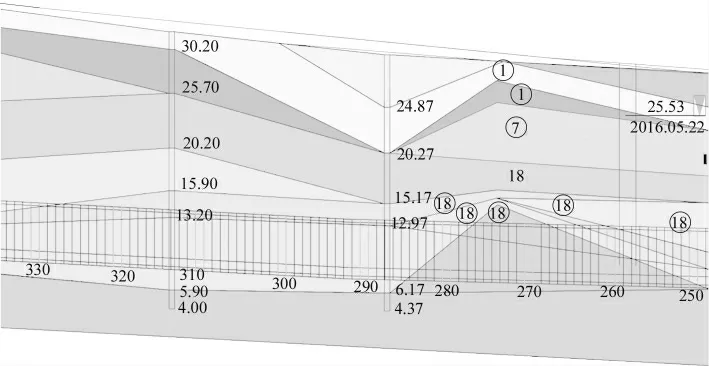
图1 深圳地铁8 号线深外站-盐田站区间右线250 环至330 环地层情况
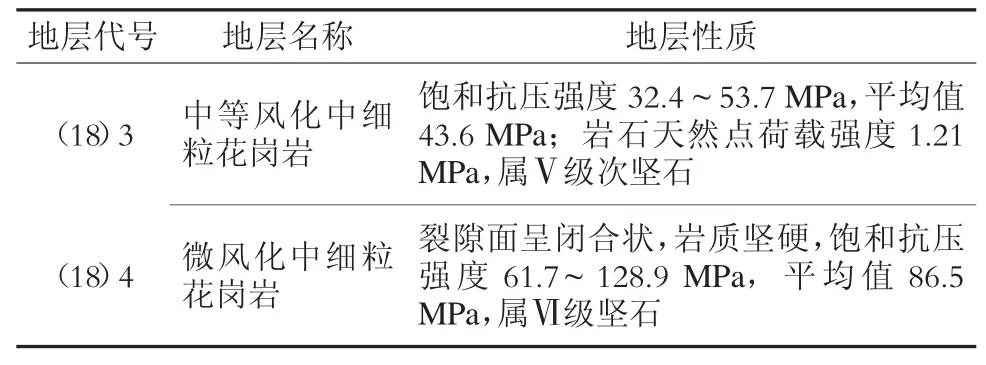
表1 深圳地铁8 号线深外站-盐田站区间右线250 环至330 环地层性质
掌子面的岩层组合和岩石性质不同,不同类型截面总体性质存在的差异对刀盘扭矩的预测会有一定的影响[16]。在不同地质类型截面的地层中掘进时,盾构掘进参数存在规律性差异,可以根据掌子面的岩层组成和围岩性质对不同区段进行分类并分别预测,进而分析土压平衡盾构机在不同区段中掘进时表现出的特性和共性,并总结出预测刀盘扭矩的通式。根据掌子面的组成和岩石种类,将250 环至330 环分为上软下硬(RY)、微风化全断面(JZ-W)和中风化全断面(JZ-Z)3 种类型(见表2)。

表2 掌子面截面分类
2 刀盘扭矩预测分析
2.1 刀盘扭矩预测模型
本文以编程语言Python 环境下的第三方库Gplearn 对现场实测数据进行符号回归,Gplearn 是目前Python 内较为成熟的符号回归算法实现方法。将数据分为训练集和测试集,训练集和测试集中数据量比例为1∶1。
掘进过程中,总推力、贯入度和土仓压力对扭矩影响较大,相较于土体参数能够实时准确得到且经济代价小。故本文选择通过总推力、贯入度和土仓压力来预测刀盘扭矩。
本工程中的符号回归算法运算过程如下:
1)随机产生初始群体。当没有经验公式或者是可靠的先验模型时,符号回归算法利用输入、输出关系,在一系列给定的运算符号(+、-、×、/等)和一组函数关系(sin、cos、tan、exp、log 等)的函数空间S 中随机生成。
2)评价个体适应度。适应度函数为:
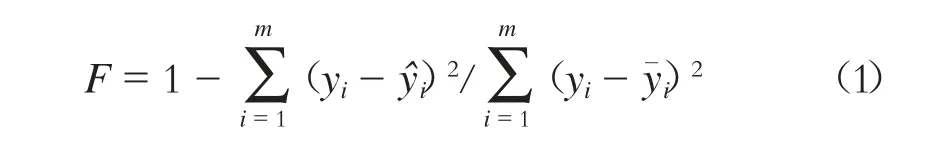
其中:yi为实测值;yˆi为预测值;y¯i为实测值平均数。
3)扭矩预测模型。如式(2),定义的函数空间S中确定的最优模型结构为:
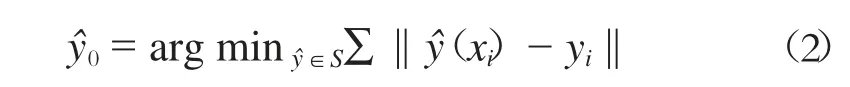
其中:yˆ0为最终解;xi为样本点i 的自变量(总推力、贯入度及土仓压应力)。
4)是否满足终止条件。 终止条件中用以评价多元非线性的拟合优度RN为:
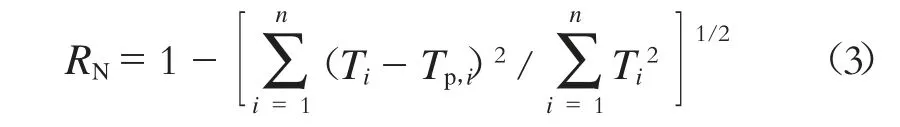
其中:Ti为样本点的扭矩实测值;Tp,i为样本点的扭矩预测值;i 为取值点的编号,n 为取值点总数。当RN≥0.95 时终止。
5)输出。得到迭代终止时的方程自变量集系数计算结果,从而得到方程的具体形式。
预测流程如图2 所示,输入自变量产生初始群体,经过变异、交叉后,得到预测扭矩的模型,对模型的适应度进行选择判断,最终得到结果。
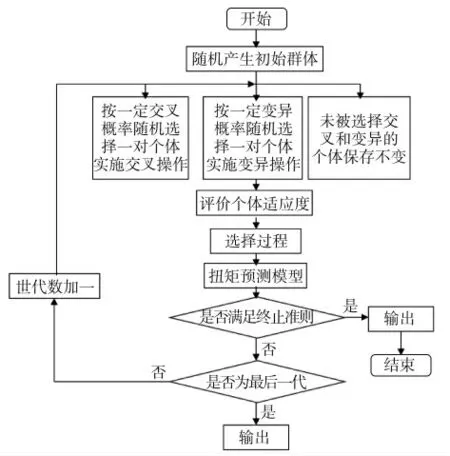
图2 预测刀盘扭矩流程图
2.2 预测结果分析
在RY、JZ-W、JZ-Z 地层的掘进过程中每30 s记录1 次掘进参数,剔除始发阶段的数据,并计算每相邻5 min 的掘进参数平均值用以消除部分环境噪音,共取2 560 组有效数据,掘进时间超过200 h,工期超过40 d。对数据进行符号回归,预测结果见表3。

表3 符号回归算法预测刀盘扭矩结果表

图3 RY 掌子面中刀盘地层扭矩预测值与观测值对比
在掌子面RY 中刀盘扭矩预测值与观测值作对比(见图3),有74%的数据其误差低于10%,其中最大误差51%、最小误差0.02%、平均误差12.0%。预测曲线的变化趋势与实测数据的变化趋势吻合,误差主要集中在258 环。在258 环处常压开仓更换了2把中心刀(双刃)、3 把正面刀(单刃)和5 把边缘刀(单刃),其中有3 把正面刀和2 把边缘刀发生偏磨,刀具平均磨损5.09 mm。开仓操作及相应的停机-重新开机阶段,在刀具更换的条件下,刀具与掌子面间的接触面积降低,刀盘与掌子面的相互作用先降低后升高;这一阶段的掘进速率、刀盘扭矩、推力、贯入度与土仓压力和其他阶段的差异较大,导致这一阶段的扭矩与其他掘进参数之间的经验关系和其他阶段之间存在差异,导致用统一经验方程预测这一阶段掘进参数时的误差较大。
在掌子面JZ-W 中刀盘扭矩预测值与观测值作对比(见图4),有超过50.3%的数据其误差低于10%,其中最大误差62%、最小误差0.03%、平均误差9.0%。误差主要集中在275 环。在275 环处常压开仓更换了4 把中心刀(双刃)、3 把正面刀(单刃)和4把边缘刀(单刃),刀具平均磨损8.24 mm。
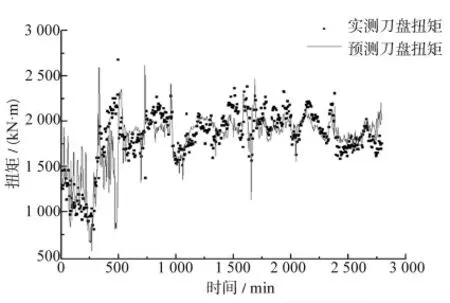
图4 JZ-W 掌子面中刀盘扭矩预测值与观测值对比
在掌子面JZ-Z 中刀盘扭矩预测值与观测值作对比(见图5),有超过74.3%的数据其误差低于10%,其中最大误差28.7%、最小误差0.002 9%、平均误差7.1%。预测曲线的变化趋势与实测数据的变化趋势吻合,精度较高。误差主要集中在322 环,是因为在322 环处,常压开仓更换了17 把正面刀(单刃)和4 把边缘刀(单刃),其中有2 把正面刀偏磨、1 把正面刀有缺口,刀具平均磨损9.82 mm。
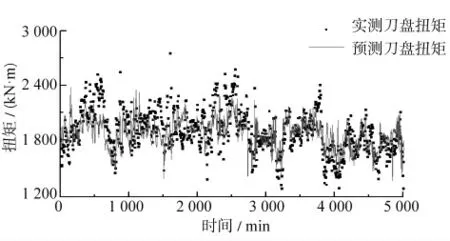
图5 JZ-Z 掌子面中刀盘扭矩预测值与观测值对比
由于地层存在非均匀性和变异性,而掘进参数分析时没有可靠的取样及观测手段,难以将由此导致的异常仪器数值进行识别和剔除。故本文分析中,各地层均未剔除异常掘进参数,但异常参数在总体数据中占比极小,对预测模型的影响较小,所以模型具有较好的精确度。模型能很好地预测刀盘扭矩的变化趋势,RN都超过0.85,并且形式简洁,没有复杂的运算过程,工程适用性较高。但是,一次性更换数量过多的刀具会对预测有一定的影响。
2.3 变量敏感性差异的定量分析
对模型变量进行敏感性分析,讨论自变量x(总推力、贯入度以及土仓压应力)发生变化时对目标变量T(刀盘扭矩)产生的影响,主要考察自变量对目标变量的积极率和消极率。
积极率Pp和消极率Np是指x 的增加引起T 增加和减小的概率,计算式为:
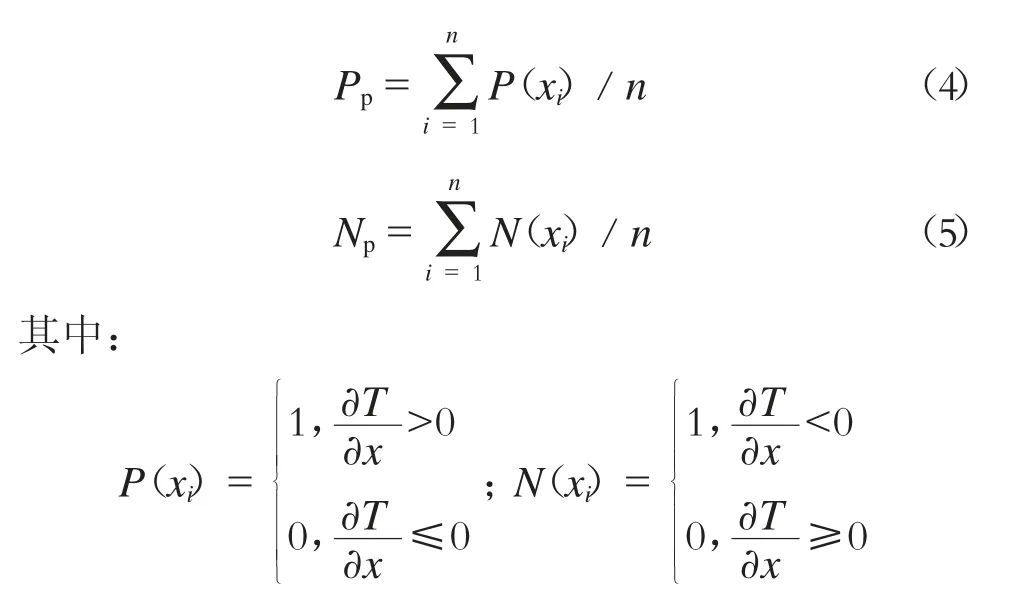
如表4 ~6 所示,对RY、JZ-W、JZ-Z 3 个掌子面刀盘扭矩的预测方程分别进行敏感性分析。在RY 掌子面的预测模型中:随着推力的增大,刀盘扭矩有63%的概率可能增大;随着土仓压应力的增加,刀盘扭矩会随之增长。在JZ-W 掌子面的预测模型中:随着推力的增大,扭矩有82%的概率可能增大;随着土仓压应力的增加,扭矩有减小的可能。在JZZ 掌子面的预测模型中:随着推力的增大,扭矩会随之增长;随着土仓压应力的增加会使得扭矩减小。在250 ~330 环的预测模型中,贯入度的增加一定会导致刀盘扭矩的增加。
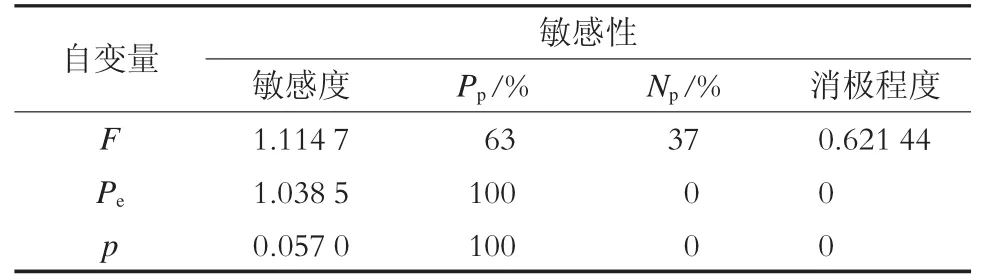
表4 RY 掌子面刀盘扭矩预测方程的敏感性分析
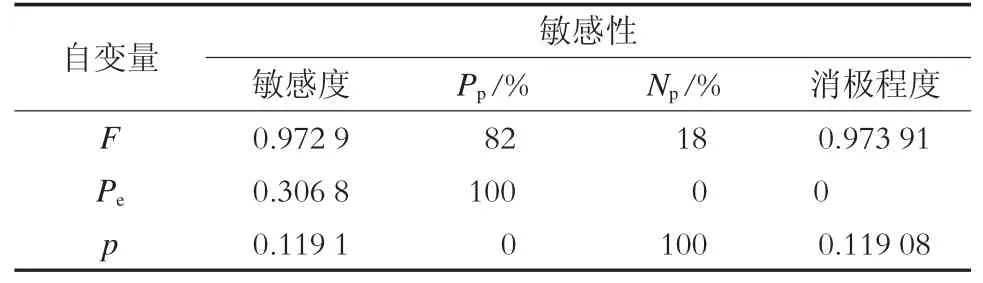
表5 JZ-W 掌子面刀盘扭矩预测方程的敏感性分析
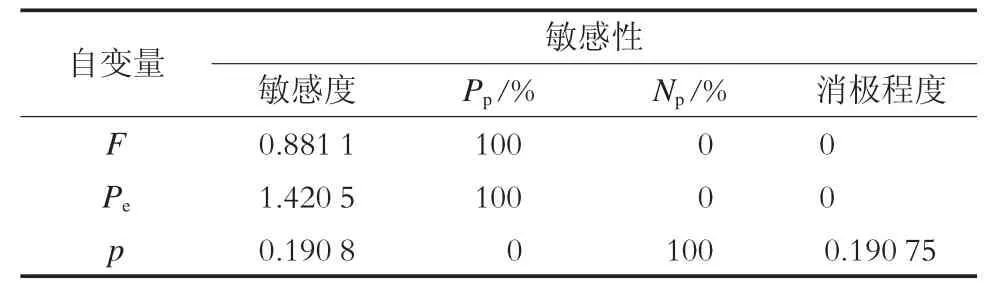
表6 JZ-Z 掌子面刀盘扭矩预测方程的敏感性分析
2.4 工程应用措施
施工中的掘进参数初定采用“先模型计算试掘、上限判定、选择性组织会议确定”的方法,首先用表3 中根据已有里程数据得到的预测方程,输入掘进参数试算值得到扭矩预测值,不断筛选试算结果,将小于扭矩警戒值的相应掘进参数作为初定值进行盾构掘进。根据盾构机在初定值条件下的掘进参数实测值与掘进参数警戒值的比较结果,将超出警戒值的相应掘进参数剔除,保留剩余掘进参数作为实际施工选用的参数值。
剩余的掘进参数均可用于盾构掘进施工,但由于各组参数之间存在差异,可以在会议中对这些参数进一步进行定性筛选。例如,当以掘进参数F=8 000 kN、Pe= 3.5 mm/r、p = 0.12 MPa 在RY 地层掘进时,预测刀盘扭矩约1.4 MN·m,小于警戒值1.7 MN·m,但存在较大的波动,最大扭矩可达2 MN·m。经分析可能是(18)4 层存在局部硬岩凸起或孤石,会议中对这一特殊情况讨论决定调整掘进参数为F=9 000 kN、Pe=2.8 mm/r、p=0.12 MPa,预测刀盘扭矩约1.4 MN·m。但由于转速降低后刀盘与孤石或下方硬岩的冲击荷载降低,刀盘扭矩实测值波动减弱,最大扭矩约1.7 MN·m。所以,调整后的参数一方面可以保护刀具和主轴,另一方面可以通过提高刃部压强提高破岩效率。参数调整后刀具因冲击荷载损坏的概率降低,从而降低了开仓换刀的频率,减少了停工时间。
所以,基于符号回归算法的盾构刀盘扭矩预测模型不但是具有统计学意义的数学模型,而且还是具有一定物理意义的模型。模型中自变量变化引起目标变量的变动,既符合现实情况,又能够体现“在提高掘进效率的前提下保护设备”这一工程原则,有利于在实际操作中指导地层变化时的人工干预。
3 结论
1)符号回归算法能较好地模拟盾构掘进过程中刀盘扭矩的变化。刀盘扭矩预测模型的预测精度较高,对盾构施工有一定的指导作用。
2)在硬岩条件下,盾构机掘进过程中贯入度加大一定会引起刀盘扭矩的增加;增大推力的同时适当降低刀盘扭矩,能够有效破岩并保护盾构;土仓压应力变化程度较小,对刀盘扭矩影响较小。
3)利用刀盘扭矩预测模型指导盾构施工,结合相应的工程应用措施,可减少刀具非正常磨损破坏发生的次数,降低了开仓换刀停工时间和施工成本,提高了施工效率。
基于符号回归算法的盾构刀盘扭矩预测模型反映了掘进参数之间的经验关系,但是该模型尚不能清晰反映地层条件对预测的影响,模型的拟合精度上也存在提升空间。

