基于农产品期货的跨品种套利投资策略研究
葛腾飞,刘佳豪,陈 龙,徐 静
(马鞍山学院 经济与管理学院,安徽 马鞍山 243100)
我国农产品期货市场自20世纪90年代建立以来,已涵盖粮、棉、油、糖四大农产品期货品种系列。目前,市场处于良性的健康发展轨道,农产品期货市场价格逐渐成为重要的市场指导价格。期货农业以其风险性低、价格提前发现、农民增收效益显著等优点被农产品交易市场和广大农户所接受。其中,豆类期货市场规模较大,居于农产品期货首位,约占农产品期货市场成交额的70%。我国是大豆的原产地,也是最大的大豆生产和消费国之一,大豆是我国主要的粮食作物之一。大豆下游产品有豆油和豆粕,产业链联系密切。豆粕是经大豆压榨后得到的一种副产品,它可以用作家禽饲料的主要原料,也可用于制作食品和一级化妆品。在大连商品交易所中,大豆和豆粕合约交易非常活跃,而且两者存在很高的相关性。目前,国内对农产品期货套利问题的研究并不充分,本文主要研究大豆和豆粕期货价格之间的相互关系,讨论是否存在套利机会,并通过对豆类期货市场的分析为投资者提供农产品套利的策略。
现有研究表明,农产品期货的跨品种套利投资在金融投资领域有重要研究价值。有学者基于对棕榈油、豆油以及菜籽油期货主力合约的相关性分析,得出期货合约价格之间是相互协整的结论,进而制定相应的跨品种套利策略。[1]有研究进一步提出并验证了协整模型、误差修正模型和基于协整关系的CARCH模型等三个统计套利模型以及相应的策略在我国期货市场的可行性。[2]学者汪哲宇等以黄大豆1号为例,采取四种计量模型分阶段评估我国农产品期货与现货的价格发现功能的效率。[3]有学者以大豆和豆粕期货为例,首先通过确定两种农产品期货价格之间具有平稳性,建立误差分析模型,进而拟合两者之间的相关关系,发现相互之间的影响关系不同于现货市场一般的生产关系,豆油对豆粕、豆粕对大豆的影响关系最为明显,实证研究得出豆粕比较适合跨交割期限套利交易的结论。[4-6]还有学者通过大豆及其衍生品之间、原油及其衍生品之间、不同原油品种之间套利,全面研究跨品种期货套利,为跨品种套利理论发展和实务应用提供了理论借鉴。[7]当然,研究跨品种套利时要将理论与实证相结合,在丰富跨品种套利理论的同时,推进我国期货套利市场不断完善。[8]本文基于上述理论基础,通过大豆和豆粕期货合约价格的协整关系检验,以及在此基础上利用套利利润期望函数计算交易阀值,并用VaR方法确定风控阀值制定套利策略,最终通过套利效果评估,验证套利策略的可行性。
一、投资策略模型构建
跨品种套利是指买入或卖出某种期货合约的同时,卖出或买入相关的另一种期货合约,这两种合约之间存在相对稳定关系,两个期货合约价差的时间序列往往围绕着均值上下波动,即使有偶尔的、短暂的震荡,但最终能回到均值。当两者的差价脱离正常轨道时,在有利时机将这两种合约对冲平仓从而获利。根据经验判断和量化模型选择,做空价值被高估合约,做多价值被低估合约,即在交易过程中,当价差达到波峰时,产生进场信号;当价差达到均值处,产生离场信号。当合约价差偏离均值一定程度时出现套利机会,这时可以采用均值回复的套利策略。本文基于大豆、豆油和豆粕三者之间存在的密切价格关系,而维持这种关系的正是大豆的压榨率。
根据朱丽蓉等人的研究,大豆的压榨利润计算公式为:
压榨利润=豆油价格×出油率+豆粕价格×出粕率-大豆价格-加工费
(1)
构造大豆和豆粕期货价格之间的线性回归模型:
dadout= β0+β1doupot+ εt
(2)
其中,dadout是大豆期货合约价格时间序列,doupot是豆粕期货合约价格时间序列。
那么,dadout、doupot时间序列的价差为:
spreadt=dadout-β0-β1doupot=εt
(3)
其中,价差就是负的压榨利润,研究价差的波动等于研究压榨利润的波动。在大豆出粕率与加工费用难以确定的情况下,可以用二者之间长期稳定的均衡关系作为合理的压榨利润关系,根据模型(3)所求出的β0和β1即为合理的加工费用和出粕率。
二、投资策略实施
1.样本选取
以大连商品交易所上市的大豆和豆粕期货合约为研究对象,选取2010-01-04到2015-01-05连续合约日收盘价为样本内研究数据,共1 456组数据,对样本内进行套利策略分析;另外,选取2015-12-31到2017-12-29连续合约日收盘价为样本外研究数据,共732组数据,对样本外进行套利策略分析(数据来源于同花顺iFinD)。
2.相关性分析
用dadou、doupo表示大豆和豆粕期货合约价格时间序列,从图1可以看出,两个期货合约价格的走势之间具有较强的相关性。进一步求出二者间的相关系数为0.7392,说明两者之间具有较高的相关性。因此,可进一步检验两个时间序列之间是否存在协整关系,即长期均衡关系。

图1 样本期内大豆和豆粕期货价格走势图
3.单位根检验
在探究变量之间的协整关系之前,须对每个变量采用ADF方法进行平稳性检验,从而判断所有变量是否满足协整前提,即是否为同阶单整。对dadou、doupo两个时间序列进行单位根检验,结果见表1。
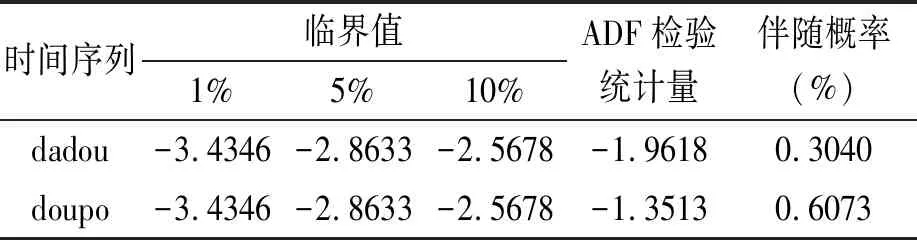
表1 dadou、doupo的单位根检验结果
由表1可以看出,在1%、5%、10%的显著性水平上,两种期货合约价格序列的ADF检验值都大于临界值。因此,接受原假设,说明二者都是非平稳序列。对两个期货合约价格序列分别进行差分,即对△dadou、△doupo进行ADF检验,结果见表2。
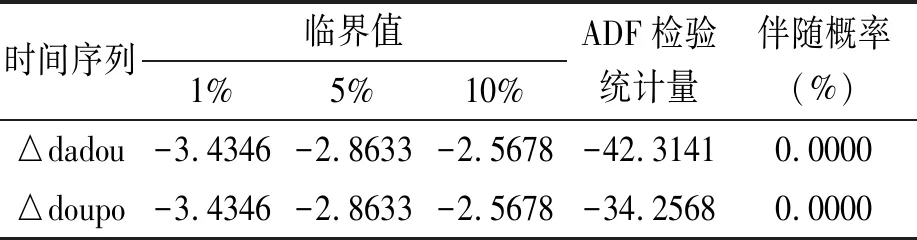
表2 △dadou、△doupo的单位根检验结果
由表2可以看出,ADF统计量值都小于临界值,伴随概率接近于0,拒绝原假设,说明两个期货价格的差分序列为平稳序列,满足进行协整分析的前提条件。
4.协整检验
(1)OLS估计方程
大豆和豆粕期货价格之间的线性回归模型:
dadout=β0+β1doupot+ εt
(4)
用Eviews分析,得出OLS估计结果:
dadout=2516.97 +0.5950doupot
(5)
常数C=2516.97是加工费用,包括人力成本、机器折旧、动力成本等在压榨期间产生的直接费用,豆粕β1=0.5950。系数均通过显著性检验,拟合度R2=0.5434,拟合度较好。
(2)提取残差序列Residual
运用ADF方法对残差序列进行单位根检验。从结果可以看出,统计量T=-2.9298,Prob.=0.0422,说明残差序列在5%的置信水平下是平稳的,表明大豆和豆粕期货合约价格时间序列存在协整关系,即长期均衡关系。
5.误差修正模型
通过协整检验得到大豆、豆粕期货合约的长期协整关系,但是这种长期的均衡关系是在短期的不断调整中实现的,需要进一步对短期的误差回复形式进行分析。
通过对大豆、豆粕期货合约价格进行OLS回归分析,可以得到下述残差序列:
et=dadout-2516.97-0.5950doupot
(6)
令ecmt-1=et-1,构建误差修正模型如下:
△dadout=α0+α1△doupot+γecmt-1+εt
(7)
其中,△dadout=dadout-dadout-1,△doupot=doupot-doupot-1。
对带有常数项的误差修正模型进行OLS回归分析,得出常数C伴随概率为0.8741,未能通过显著性检验,因此去掉常数项再进行估计。对不带有常数项的误差修正模型进行OLS回归分析,得出:
△doupot的系数=0.2885,γ=-0.0219
由估计结果得出误差修正模型为:
△dadout=0.2885△doupot-0.0219ecmt-1
(8)
在误差修正模型中,误差修正系数γ代表着短期波动对长期均衡的修正程度。估计结果中误差修正系数为-0.0219,说明前一期的非均衡误差将以2.19%的比率对△dadout进行反向修正,使之向长期均衡回复。
同时,利用半周期公式:
(9)
计算得出T=62,说明从偏离均衡关系到回复均衡需要将近62个交易日,回复速度较慢。
根据长期均衡关系,构建两个期货价格时间序列的价差序列,然后再对其进行去中心化处理:
spreadt=dadout-2516.97-0.5950doupot
(10)
mspreadt=spreadt-mean(spreadt)
(11)
根据去中心化价差序列走势图和描述统计分析可知,去中心化价差序列mspreadt是服从正态分布的。因此得出大豆:豆粕的套利头寸为1:0.5950。当mspreadt大于设定的阀值时,说明大豆期货合约价格相对被高估,则应卖出1手大豆期货合约,买入0.5950手豆粕期货合约,持有合约直至mspreadt回复到均衡值进行平仓;反之,当mspreadt小于设定的阀值时,说明大豆期货合约价格相对被低估,则应买入一手大豆期货合约,同时卖出0.5950手豆粕期货合约,持有合约直至mspreadt回复到均衡值进行平仓。
6.交易与风控阀值的确定
阀值对于整个交易过程具有重要意义,本文需要计算交易阀值和风控阀值。由确定的投资组合比例,构建可供交易的区间,将这种区间分为三种情况:一是无套利区间,在此区间内,看做没有套利的机会,无法进行套利;二是套利区间,在此区间内,存在套利机会,建仓买入;三是止损区间,当交易值达到此区间,应平仓止损。
(1)交易阀值的确定
假设上下交易阀值不存在对称性,利用套利利润期望函数来求得上下交易阀值。本文用kupperσ表示上阀值,用klowerσ表示下阀值(σ是mspreadt序列的标准差)。当mspreadt>kupperσ时,卖出大豆期货合约,同时买入豆粕期货合约,持有合约直至mspreadt回复到均衡值进行平仓;反之,当mspreadt<-klowerσ时,买入大豆期货合约,同时卖出豆粕期货合约,持有合约直至mspreadt回复到均衡值进行平仓。如果kupperσ、klowerσ的取值太小,就会导致频繁的交易,增加交易成本,一方面会造成利润的侵蚀,另一方面还有可能造成亏损;如果kupperσ、klowerσ的取值太大,交易机会就会很少,不能很好地获得交易的利润。
假设套利利润期望函数为:
E(kσ)=λ{kupperσP(mspreadt>kupperσ)+klowerσP(mspreadt<-klowerσ)}
(12)
其中:λ是一个特定的正常数,P(mspreadt>kupperσ)表示mspreadt>kupperσ的概率,且
P(mspreadt> kupperσ)= nupper/N
(13)
P(mspreadt<-klowerσ)表示mspreadt<-klowerσ的概率,且
P(mspreadt<-klowerσ)=nlower/N
(14)
其中nupper是mspreadt>kupperσ的个数,nlower则是mspreadt<-klowerσ的个数,N是样本内的总个数。kupper、klower的取值,应该能使E(kσ)最大,所以分别让kupper、klower按照0.01的步长从0到3取出300个值,在此基础上加以计算P(mspreadt>kupperσ)和P(mspreadt<-klowerσ)。计算结果如图2所示。
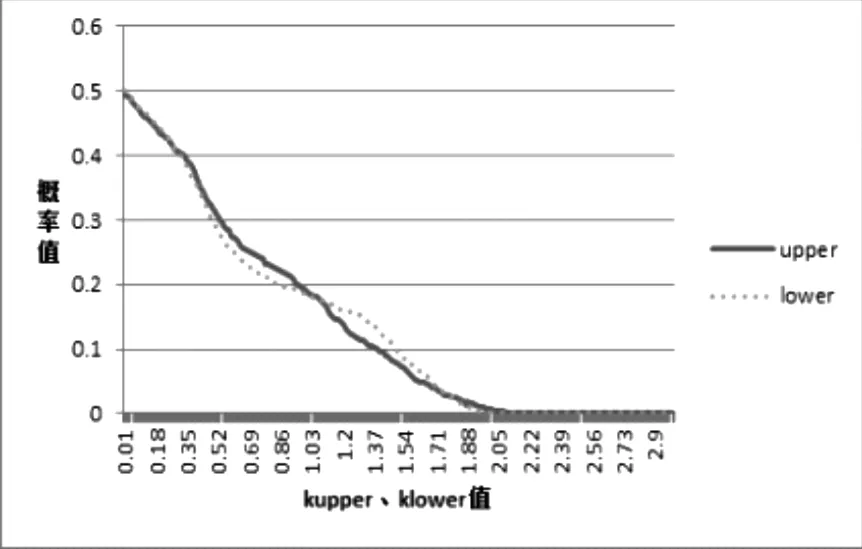
图2 kupper、klower变化时P的变化趋势
根据套利利润期望函数(式12),其中,假设λ=5,求出阀值取kupperσ、klowerσ时的期望收益(见图3)。从图3可以看出,当kupper=0.92、klower=1.28时期望收益最大。所以,本文将0.92σ和-1.28σ作为样本内数据的上下交易阀值,并且将样本内的交易阀值同样作为样本外的交易阀值。
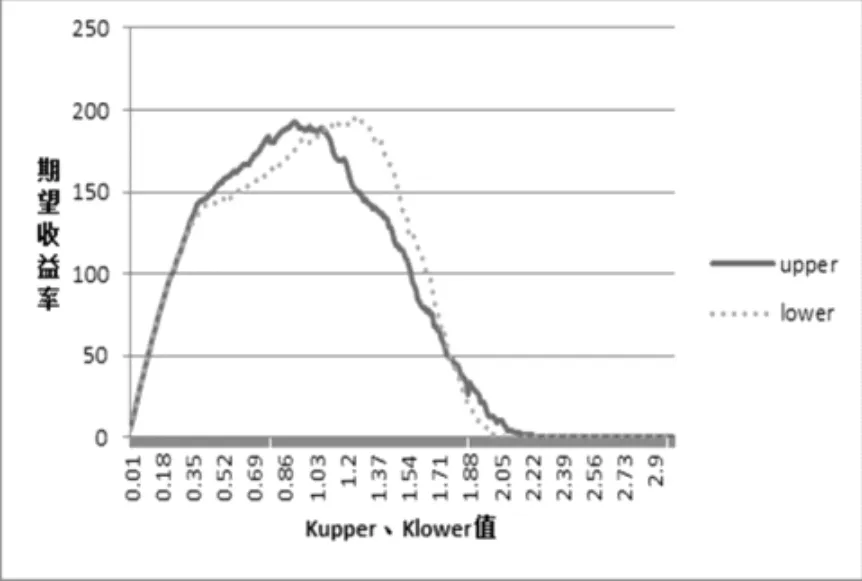
图3 kupper、klower变化时套利期望收益的变化趋势
(2)风控阀值的确定
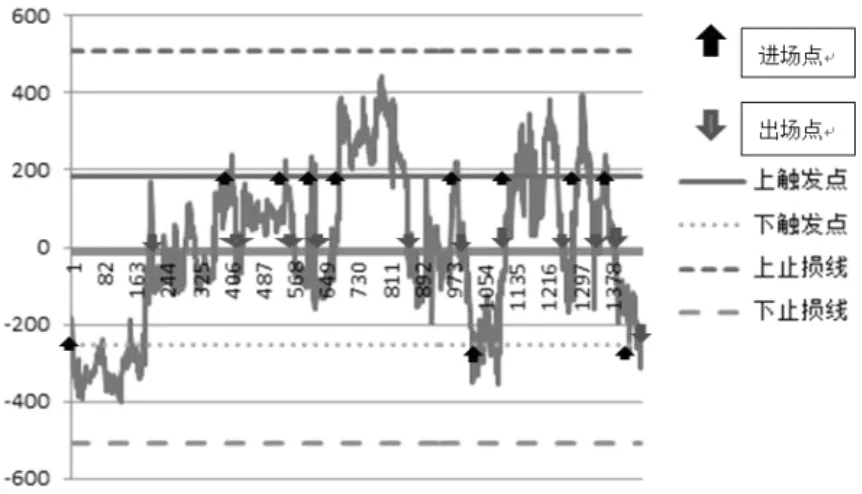
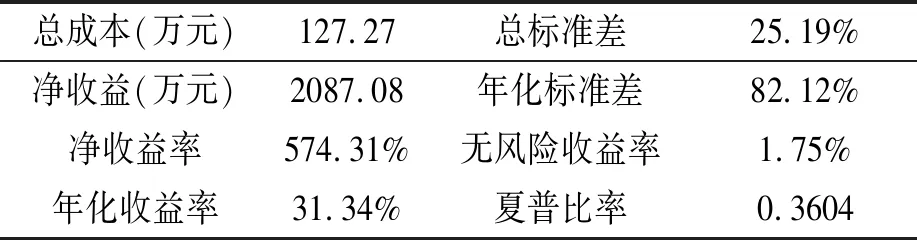
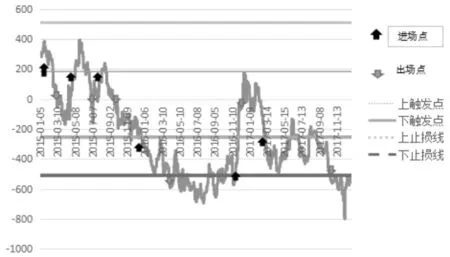
期货跨品种套利过程中,在建立套利头寸后,当mspreadt>Z0.995或者mspreadt VaR用公式表示为: P(△P△t≤VaR)=a (15) 其中,P是资产价值损失小于可能损失上限的概率;ΔP是某一金融资产在一定持有期Δt的价值损失额;VaR是给定置信水平a下的在险价值,即可能的损失上限;a是给定的置信水平。VaR从统计的意义上讲,本身是个数字,是指面临“正常”的市场波动时“处于风险状态的价值”。即在给定的置信水平和一定的持有期限内,预期的最大损失量(可以是绝对值,也可以是相对值)。 由上文的mspreadt统计分析的Jarque-Bera检验数据可知,mspreadt~N(0,198.19)。在1%的置信度下,Z0.995={Z0.995P(mspreadt (16) 根据mspreadt序列的标准差和标准差正态分布分位表计算可知,Z0.995=509.35。所以,本文将509和-509作为样本内数据的上下风控阀值。 (3)套利操作过程 开仓:当价差超过上阀值0.92σ时,卖出大豆期货合约同时买入豆粕期货合约;当价差低于下阀值-1.28σ时,买入大豆期货合约同时卖出豆粕期货合约。平仓:当价差回落至均值水平或者均值附近时,进行平仓。止损:当价差超过交易上阀值0.92σ后没有回复到均值,而是继续偏离均值至风控上阀值509时轧平头寸止损;当价差低于交易下阀值-1.28σ后没有回复到均值,而是继续偏离均值至风控下阀值-509时轧平头寸止损。 1.样本内套利策略收益分析 根据套利投资策略建立的套利头寸,大豆:豆粕=1:0.5950,也就说卖出1手大豆期货合约,同时买入0.5950手豆粕期货合约;反之,则买入1手大豆期货合约,同时卖出0.5950手豆粕期货合约。当价差回落至均值水平(或者均值附近)时,或者继续偏离均值至风控阀值时轧平头寸止损。根据大连商品期货交易所公布的期货合约最高交易手续费可知,大豆期货合约交易手续费是4元/手,豆粕期货合约交易手续费是3元/手;每次的开仓费用是5.7850元,平仓费用是5.7850元,总费用是11.57元。两种期货合约的保证金比率为5%。假设起始资金为100万元,买卖大豆和豆粕的手数可以按套利头寸进行交易,即只买入1手大豆时卖出0.5950手豆粕或卖出1手大豆时买入0.5950手豆粕。 根据上述的套利策略对样本内数据进行模拟交易,得出如下的套利机会(见图4)。 图4 样本内套利进出点示意图 由图4可知,样本内一共可以进行11次套利,对上述结果进行计算整理,得出整个样本期内模拟效果(见表3)。 表3 样本内套利效益风险分析 其中,净收益率为11次套利的累计收益率,年化收益率是采用复利进行计算的,公式为: (17) R1就是年化收益率,R是2010—2015年的累计收益率,总标准差σ是收益率序列的标准差,年化标准差是σ1, (18) 无风险收益率采用银行一年期定期存款利率1.75%。理性的投资者会选择在一定的风险水平下,期望回报率最大的投资组合,或者在一定期望回报率的水平下,风险最小的投资组合,要求尽可能以最小的风险代价来换取尽可能大的回报。因此,本文选用夏普比率来测定投资策略的风险性,比率越大则套利策略效果越好。其计算公式为: (19) 其中,Rp是组合收益率,Rf是无风险利率,σp是组合收益率的标准差。由表3可以看出,样本内套利的年化收益率为31.34%,收益率较高;年化标准差为82.12%,说明风险较高;夏普比率为0.3604,表明套利投资策略套利效果收益与风险成正比,享有较高收益的同时,也需承担较高的风险。 2.样本外套利策略收益分析 本文假设市场存在连续合约,以2015-12-31到2017-12-29连续合约日收盘价为样本外研究数据,共732组数据。根据样本内数据做出的长期均衡关系式为: spreadt=dadout-2516.97-0.5950doupot (20) 通过该关系式可以得到样本外数据的价差序列,再进行去中心化处理。 通过样本内数据得出交易阀值和风控阀值,交易上阀值0.92σ,为182.34;下阀值-1.28σ,为-253.69;风控上阀值为509,下阀值为-509。将其作为样本外模拟交易的阀值,得出套利进场机会(见图5)。 图5 样本外套利进出点示意图 由图5可以看出,样本外共有6次套利机会。对其结果计算整理,得出整个样本外模拟效果(见表4)。 表4 样本外套利效益风险分析 由表4可以看出,样本外套利的年化收益率为35.10%,年化标准差为62.49%,夏普比率为0.5337,说明本套利策略在样本外的检验是可行有效的。 本文研究了大豆和豆粕期货市场之间的跨品种套利交易。通过分析大豆、豆粕两品种具有良好跨品种套利条件,实证检验大豆、豆粕期货市场的有效性以及两品种的相关性,建立两种农产品期货合约的协整关系来确定套利头寸,在价差序列统计特征的基础上建立交易阀值,并用VaR方法确定风控阀值,从而制定了统计套利策略。通过实证检验,得出样本内总收益率为31.34%,样本外总收益率为35.10%。 基于上述研究结论,提出以下建议:一是套利虽然是一种风险相对较低的投资,但是并不意味着没有风险,在进行套利交易时务必要设好止损位,做好风险控制。二是本文是在假设存在连续合约的基础上进行分析的,与现实情况存在一定出入,因此在进行农产品跨品种套利时,要关注合约的交易时间,做好交接,同时成本也会有所增加。三、实证检验

四、结论和建议

