机器人路径规划的遗传算法求解策略分析
杨 平, 谭代伦
(1.西华师范大学数学与信息学院,四川南充 637009;2.西华师范大学计算方法及应用软件研究所,四川南充 637009)
0 引言
随着智能技术的发展,移动机器人已被广泛应用到军事、工业、商业及家庭生活等各个领域[1].路径规划是移动机器人工作的基础,根据作业环境的不同,移动机器人的路径规划可分为两类.一类是基于机器人自身安装的环境信息传感器对未知环境信息实时获取的局部路径规划,也称为动态路径规划.另一类是基于全局地理信息的路径规划,也被称为静态路径规划[2].静态路径规划通常是指机器人的作业环境中分布着一些障碍物,在给定的起点和目标点之间为机器人规划一条安全、高效的免碰撞路径[3].通常满足避障条件的路径不止一条,在具体问题中需要根据不同的目标,例如路径长度最短、用时最少、能量消耗最小等,寻找出一条最优路径[4].
针对机器人路径规划,国内外学者提出了很多方法,常见有可视图法[5-7]、栅格法[8-9]、A*及其改进算法[10-11]、蚁群算法[12-14]、遗传算法[15-17]等.其中,模拟生物进化过程的遗传算法(Genetic Algorithm, GA)具有灵活性好、鲁棒性强和不易陷入局部最优等优点.已有文献研究表明,遗传算法在机器人避障路径规划问题中求解中取得了较好的效果.不少学者做了一些改进性的研究工作,并取得了一定的研究成果.如文献[18]提出的基于分组和精英策略的遗传算法,加快了算法的收敛速度.文献[19]对遗传算法的交叉、变异算子进行了改进,提高了算法的进化能力.
已有文献资料主要研究遗传算法的改进以提高收敛速度和求解精度,但较少涉及遗传算法的不同求解策略对求解效果的影响.为此,本文通过构造四种不同障碍物的测试场景,分别采取遗传算法的轮盘赌策略、君主策略、锦标赛策略进行多次求解,进而分析求解效果的差异.
1 测试场景的构建
一般地,在移动机器人作业平面内的障碍物可以被近似为规则几何图形和不规则几何图形.规则几何图形主要包括三角形、矩形、圆和其他多边形,不规则几何图形主要是指障碍物的边沿轮廓复杂多变,难以用单一的规则几何图形表示.为方便设计避障算法,测试不同求解策略的性能,本文主要构造由单个几何图形或它们简单混合的测试场景,如图1.
在图1中,移动机器人在一个水平方向和竖直方向都为20个单位长度的二维平面内行走,左下角坐标为(0,0),右上角坐标为(20,20),分别为机器人行走的起点和终点.场景(a)和(b)由单个障碍物构成,均位于平面的正中央处,(a)图中圆的圆心为(10,10),半径为2;(b)图中正方形边长为4.场景(c)和(d)是由矩形、正方形和圆形三个规则图形混合构成,其中圆的半径仍为2,矩形的长为5、宽为2,正方形的边长为4.在实验中忽略机器人自身的大小,将其视作一个移动的质点.

图1 不同类型障碍物的测试场景Fig.1 Test scenarios for different obstacle types
2 遗传算法的设计
2.1 个体编码与初始种群

图2 个体染色体及其基因编码Fig.2 Individual chromosome of path and its gene coding
遗传算法的个体染色体编码影响着遗传算子的操作,进而影响到算法的收敛.在机器人作业平面内,移动路径节点由平面内的若干个坐标点构成.为了提高计算精度,增强遗传算法的避障和穿越能力,本文采用二维实数对编码,即取每一个节点的二维实数坐标(xi,yi)为一个基因编码,设路径节点数为n,全部节点构成一条染色体(路径)编码,即一个个体的编码,如下图2所示.
路径节点数n即为个体基因编码长度,由于机器人作业平面不大、场景中障碍物较少,因此n的取值在5~10内可获得较好的求解效果.另设个体的种群规模为M,节点的二维实数坐标构成本问题的双种群,分别记为X=[X1;X2;…;XM],Y=[Y1;Y2;…;YM].
2.2 与障碍物相交的判断算法
路径规划的首要目标就是要使机器人能够避开障碍物,获得一条不与障碍物发生碰撞的安全路径.下面首先给出路径与圆形和矩形障碍物是否相交的判断算法.
算法1:与圆形障碍物相交的判断算法.
输入:圆形障碍物的圆心坐标和半径:C(xC,xC),r;
路径上第i条线段的两个端点坐标:Ai(xi,yi),Ai+1(xi+1,yi+1).
输出:线段是否能避开障碍物的判断变量ri.
(1)计算线段CAi,CAi+1的长度|CAi|,|CAi+1|,令li=min{|CAi|,|CAi+1|}
(2)若lir,则Ai,Ai+1至少有一个点在圆形障碍物内部,即不能避开,则置ri=0,算法结束;否则继续.
(3)根据顶点Ai,Ai+1坐标,计算AiAi+1直线一般方程的系数:ai,bi,ci.
(4)计算圆心C到直线AiAi+1的距离,记为di,计算公式为:
(5)计算圆心C到直线AiAi+1的垂足坐标,记为D(xdi,ydi),计算公式为:
(6)若dir且xi(xi+1) 算法2:与矩形障碍物相交的判断算法 输入:矩形四个顶点的坐标:B1(x1,y1),B2(x2,y2),B3(x3,y3),B4(x4,y4) 路径上第i条线段的两个端点坐标:Ai(xi,yi),Ai+1(xi+1,yi+1). 输出:线段是否能避开障碍物的判断变量ri. (1)置ri=1,令k=1,取矩形的顶点Bk(xk,yk),Bk+1(xk+1,yk+1) (2)构造向量AiAi+1,BkBk+1,AiBk,AiBk+1,BkAi+1,BkAi (3)根据向量坐标作向量叉乘,计算公式如下: p1=AiAi+1×AiBk,q1=AiAi+1×AiBk+1 p2=BkBk+1×BkAi,q2=BkBk+1×BkAi+1 (4)若p1q10且p2q20,则线段AiAi+1与矩形的边BkBk+1相交,即不能避开障碍物,则置ri=0,算法结束;否则继续. (5)令k=k+1,若k=4则算法结束,否则转到步骤(1). 适应度函数是用来度量种群中的每个个体是否能够达到或者接近最优解的优良程度,适应度高的个体遗传到下一代的概率更大.在机器人路径规划问题中,其最优目标是使行走路径尽量短,需要满足的约束是不与场景内任何障碍物发生碰撞.为降低算法计算量,减少对种群中非法个体的筛选和过滤,本文采用罚函数方法,即若一条路径穿过障碍物,则该条路径的长度被惩罚为0. 对任意一条路径A1→A2→A3→…→AN,设第i个节点Ai的坐标为(xi,yi),路径总长度分量记为f1,则有 根据3.2节中与障碍物相交的判断算法,定义如下0-1型变量: 为了便于算法的遗传操作,需使短的可行路径获得更大的适应度值,可用一个较大数C减去原有路径长度,将最小值问题转换为最大值问题.因此,最终的适应度函数为: 选择操作的任务是按照一定的规则挑选出与种群规模相同的适应度较优的个体.个体的适应度越大,被选入新种群的可能性越高,这是对自然选择中优胜劣汰的模拟.不同的选择策略对算法的求解效果有着重要的影响.[20]本文选取常用的三种策略:轮盘赌策略、锦标赛策略、君主策略,为每种策略设计了具体的步骤.在个体编码方案中,本问题是双种群的,因此下述策略对两个种群均要同步操作. 2.4.1 轮盘赌策略 轮盘赌策略是最早被提出的一种个体选择策略,它根据每个个体的适应度来计算该个体在子代中出现的概率,并根据此概率随机选择个体构成子代种群.轮盘赌策略的原理是适应度值越大的个体被选择的概率越大.因此,在求解最大化问题中可直接采用适应度值来进行选择.但对于最小化问题,必须先将问题的适应度函数进行转换为最大化问题.轮盘赌策略的基本步骤为: (2)计算每个个体的入选概率Pj=fj/F; (3)计算所有个体的累积概率,构造一个轮盘; (4)轮盘选择:生成一个区间[0,1]内的随机数,若随机数小于等于个体j的累积概率但大于等于个体j-1的累积概率,则个体j进入下一代群体; (5)重复操作(4),直至产生与父辈同样规模的种群. 2.4.2 锦标赛策略 锦标赛策略模拟了体育比赛中的分组联赛机制,基本思想是每次从种群中取出一定数量的个体构成一个小组,然后选择该组中适应度最高的个体进入子代种群.这类似于体育联赛机制中,只有每个分组的胜出者才能参加下一阶段的比赛.在遗传算法中模拟体育比赛的锦标赛机制时,为增强随机性、提高全局寻优能力,一般采用有放回式的随机采样机制,具体操作步骤如下: (1)确定锦标赛的分组大小r(称为r元锦标赛). 这里,分组规模的大小也会影响到锦标赛策略的效果,一些文献已经对此有所研究.文献[20]通过实验分析,建议锦标赛策略的分组规模大小取种群规模的60%~80%.本文在后续实验仿真中取值为r=种群规模×70%. (2)从种群中随机抽取r个个体(每个个体被选中的概率相同)组成一个联赛小组; (3)在联赛小组内,根据每个个体的适应度值,根据准则 对最大化问题:pk=max{p1,p2,…,pr} 对最小化问题:pk=min{p1,p2,…,pr} 选择组内最优个体进入子代种群; (4)重复操作步骤(2)和(3),直到子代种群达到预定的种群规模. 由于步骤(2)和(3)每次都是从原来的种群中选择r个个体,因此,在一轮中被选出来构成一个联赛小组的个体,无论是否被选入子代种群中,在下一轮操作中仍然有可能被再次选出来,但是它在新的联赛小组中,并不一定还是最优个体.这样,每个较优的个体被选中的机会更高,子代种群的平均适应度也更高,对寻找问题的全局最优解更为有利. 2.4.3 君主策略 君主选择策略是对自然种群中动物首领、蚁后等个体繁衍特点的模拟.这些个体通常拥有最好的基因,在繁衍过程中可与多个个体进行结合.在君主选择策略中,适应度最高的个体即为“君主”,它会多次参与到遗传过程中.君主策略具体操作如下: (1)选取种群中适应度值最大的个体,记为“君主”; (2)把父代种群的剩余个体按照适应度从大到小排列; (3)奇数号个体用君主替换,偶数号个体不变,生成下一代种群. 选择操作只能将初始种群中的路径保留复制到新种群中,并没有新个体产生.为保持种群的多样性,能真正实现全局寻优,还必须借助交叉和变异操作.本文的机器人路径规划问题中,起点和终点是固定的,因此这两个点不参与交叉和变异. 2.5.1 交叉策略 交叉操作作用于种群中某对个体之间,是对生物遗传过程中基因重组的模拟.通过交叉,种群会产生新的基因组合,从而可能获得比父辈更优秀的个体,达到进化的目的.本文采用单点交叉策略,基于一定的交叉概率(交叉概率通常取值为0.4~0.9)进行交叉.交叉操作作用于种群中某些相邻个体间,首先采用随机产生的方式确定交叉点位置,然后交换两个个体在该基因点后的基因片段,得到新的基因组合方式.用交叉后的新个体替换原种群中的个体,从而得到新的种群. 图3 遗传算法的流程图Fig.3 Flow chart of genetic algorithm 2.5.2 变异策略 变异操作的目的是使种群中产生新的基因型,从而扩大寻优范围避免陷入局部最优.本文采用单点变异策略,首先基于一定的变异概率(变异概率取值较小,通常取值为0.001~0.4)确定需要变异的个体,然后随机选取染色体中的一个基因位置作为变异点,最后用随机产生的新的基因替换变异点原来的基因.用发生变异后的个体替换原本种群中的个体,使种群获得新的基因型. 综合上述工作,在遗传算法的标准流程图基础上,本文的遗传算法流程图见图3. 本文程序在MATLAB 2018a中编写,遗传算法的初始参数设置为:种群规模200、迭代次数300、路径节点(基因数目)为5、交叉概率0.7、变异概率0.06. 本文共构造四个基本测试场景,经上述遗传算法求解,均能成功避开障碍物,获得最优路径.限于篇幅,下面给出场景(c)在三种不同选择策略下的求解结果,如图4.在图4(a)中,所获得的最优路径长度为29.095 8,图4(b)获得的最优路径长度为29.984 5,图4(c)获得的最优路径长度为29.369 5. 图4 三种策略下图1(c)场景的最优路径Fig.4 The three strategies are shown in Figure 1 (c) 只是一次或几次实验,不能很好地体现遗传算法的不同选择策略对有障碍物的路径规划问题的求解性能.为此,在保持上述算法参数不变的情况下,对图1的四种场景,分别使用三种选择策略各自独立运行100次,经统计记录,获得实验结果如下表1. 表1 三种选择策略对避障路径规划问题的求解性能统计Tab.1 Performance statistics of three selection strategies for obstacle avoidance path planning 续表1: 由表1可知,锦标赛选择策略求得的平均值和标准差全部小于另外两种选择策略,即锦标赛策略规划出的路径平均值更短,且具有更好的稳定性.轮盘赌策略和君主策略相比较,君主策略的平均值均小于轮盘赌策略,而且君主策略的标准差也是全部小于轮盘赌.因此,在使用遗传算法求解有障碍物的路径规划问题时,锦标赛选择具有比其他常见策略更好的求解性能,其次是君主策略,然后是轮盘赌策略. 本文针对有障碍物的机器人路径规划问题,构造了四个基本测试场景,分别选择遗传算法的轮盘赌策略、锦标赛策略和君主策略进行求解,通过运行100次的统计分析来对三种策略的求解性能进行比较,结果表明锦标赛策略优于另外两种策略.因此在使用遗传算法求解机器人路径规划问题时,采用锦标赛选择策略不仅可以避免转换适应度值的问题,而且比其他两种常见策略具有更好的求解性能.2.3 适应度函数
2.4 选择策略
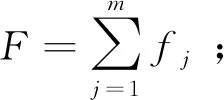
2.5 交叉与变异策略
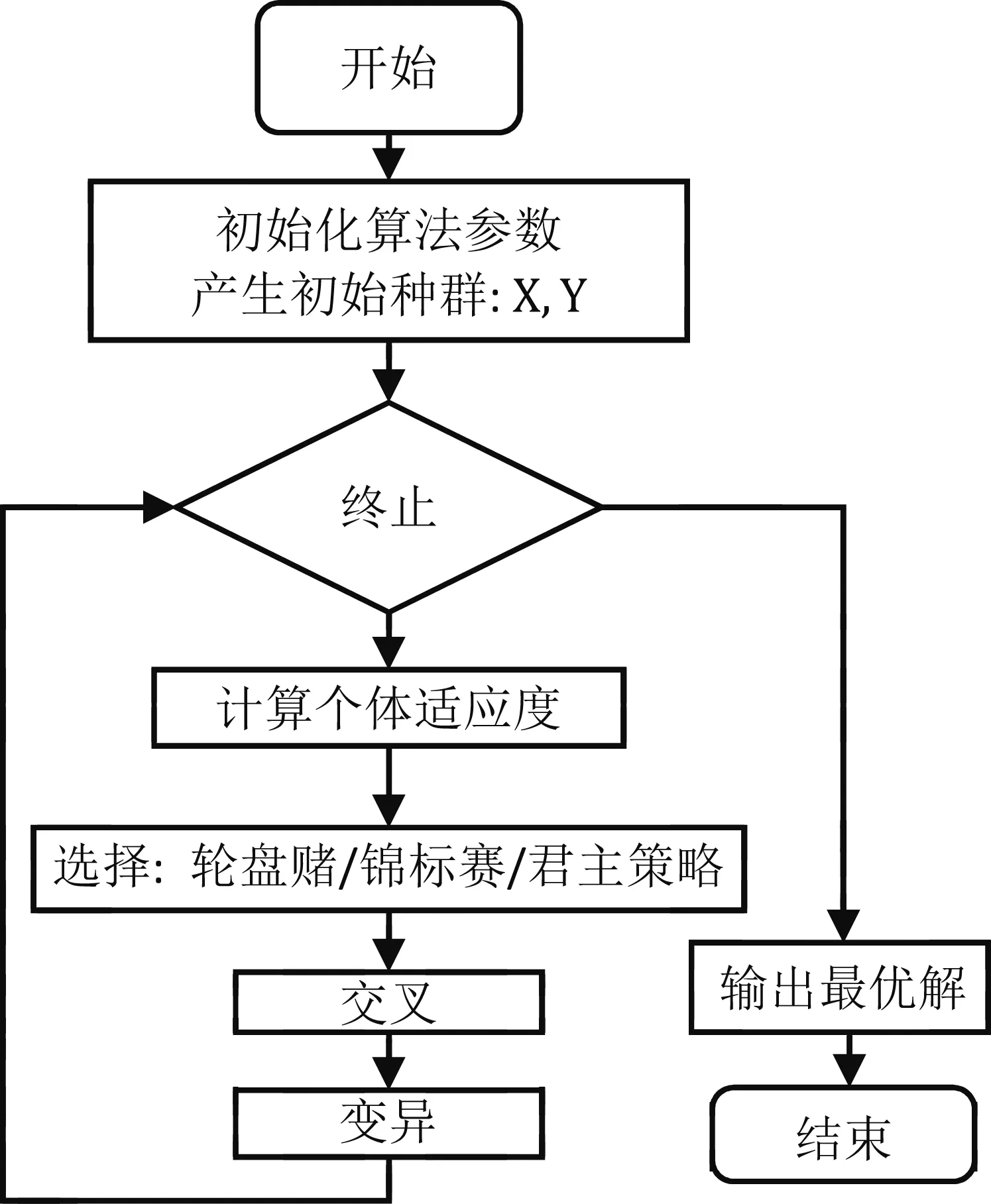
2.6 遗传算法的流程图
3 实验结果与分析
3.1 算法求解结果

3.2 求解效果分析


4 结束语

