基于二重势函数法的集群航路规划

陈天德,黄炎焱,李 琛

(南京理工大学自动化学院,江苏南京 210094)

1 引言

集群航路规划作为一个重要的研究课题,一直为集群任务规划的研究重点[1-4].

目前,集群航路规划的方法主要有领航跟随法[5]、虚拟结构法[6-7]、人工势场法[8-9]以及基于行为法[10]等.

由于无人装备的迅速发展,有人无人混合集群,甚至纯无人集群将是未来集群行动的重要形式[11].因此,集群航路规划的结果将从有人集群的参考路径转变成无人集群的行动依据,这就对集群航路规划提出了更高的要求.

单从航路规划来说,人工势场法数学模型简单[12]、解算快速[13]、易于执行且实时性良好[14],具有类人的感知特征[15].此外,所得路径平滑[16],具有易于跟随性[17],较为适用于对无人装备的航路规划[2,18-19].

集群行动必然是有构型的行动,因此集群航路规划是基于构型对集群中各单元进行航路规划.文献[20]根据期望构型中智能体之间的距离设计势场函数,可以保证智能体之间的距离最终达到期望值,而整个集群构型的运动姿态则却不能单靠势函数法来保证,可见人工势场法在队形组织能力方面略显不足.此外,当集群构型改变时,势函数参数需重新配置,从而使集群成员间保持所需距离,以此形成构型,如文献[21]将势能场布置成“沟槽”的形状,机器人运动到“沟槽”中形成队形,而不同队形需要不同形式的“沟槽”;再如文献[22]基于人工势场法研究无人机编队的导航算法,设计出新的分叉势场法,通过改变参数实现无人机编队的队形变换.因此,人工势场法在应对构型变化时使用上不够灵活[7,23].

文献[24]将构型控制与航路规划分成两个独立模块,构型控制采用人工势场的思想,通过控制集群成员间的距离来实现;航路规划采用周期进化算法获得距离代价最小的全局路径,再用类似于人工势场法的速度矢量法进行局部修正.然而,该构型控制方法,虽能形成并保持构型,但不能很好地确定集群构型的运动姿态;该航路规划算法的仿真结果表明,相比另一种以由周期性快速搜索遗传算法与人工势场法组合而成的联合算法(periodic fast search genetic algorithm and artificial potential field,PFSGA-APF)[24],该算法在路径距离上效果更优,但路径平滑度却相对差一些.

文献[7]通过设置势能场,使编队参考点到达目标参考点,而集群在势能场作用下,跟随编队参考点到达期望位置.在集群运动过程中,通过势能场控制集群成员间以及成员与编队参考点间的距离来实现构型的形成与保持.由于该构型控制中加入了编队参考点对构型的进一步约束,集群构型的运动姿态问题得到了解决.然而,当构型改变时,各成员所涉及的势函数需要进行相应的参数调整,因此该算法在使用上不够灵活,且编队参考点的个数影响对构型的约束效果,而个数确定的依据与过程并未给出.

文献[6]通过将人工势场法与虚拟结构相结合,以编队参考点为中心形成期望的虚拟结构,在势能场的作用下,集群各成员以对应的虚拟结构点为运动目标,在避碰避障的前提下,渐进形成队形.由于该方法所用的是传统的人工势场法,因此,存在着人工势场法固有的不足[16,25],且该方法仅针对编队队形的形成与保持,未涉及编队的航路规划.

人工势场法的固有不足为狭窄通道无法识别、狭窄通道中震荡、障碍在目标附近导致目标不可及(goals nonreachable with obstacles nearby,GNRON)[26]以及陷阱问题[16,25].根据文献[25]的研究结果,由于斥力势函数仅考虑与障碍物的距离因素,而导致在障碍物的影响距离范围内采取无差别避碰措施,即无谓避碰现象[27],进而产生人工势场法的固有不足.虽然固有不足产生的原因严格上讲并非唯一是无谓避碰,但若能克服无谓避碰,不仅可以在一定程度上减少固有不足问题的出现,还能提高人工势场法在路径距离上的优化效果.

针对无谓避碰问题,文献[28]通过对碰撞角和避碰角进行比较,来预测障碍物的碰撞危险,存在碰撞危险的障碍物才对机器人产生斥力作用,该方法可以较好的避免无谓避碰,但未考虑碰撞的紧迫程度,存在一定避碰不及的情况.文献[29]提出改进的斥力势函数,仅当机器人关于障碍物的相对速度在机器人指向障碍物的方向上的分量大于0且该分量减为0后机器人将移动到障碍物影响范围内时,障碍物才对机器人产生斥力作用,然而该方法能否较好的避免无谓避碰还取决于障碍物影响距离的设置.根据文献[30]的研究结果,障碍物影响距离作为势函数中一个重要参数,其值设置过大会导致规划效率低,即加剧无谓避碰的出现,过小则会导致避碰不及.目前大多数对势函数法的应用以及各方面的改进,该参数基本都被设为一个固定值.然而,在实际应用中,由于规划环境的动态性,很难得到合适的影响距离值.

本文以文献[6]的方法为基础,提出基于二重势函数法的集群航路规划算法,主要工作有:1) 借助虚拟结构的思想,将集群航路规划分为两个阶段,依次为针对集群目标的航路规划与针对集群构型的航路规划,两个阶段的航路规划均使用人工势场法;2)针对人工势场法存在的无谓避碰现象,构建碰撞危险度评估模型以及障碍物影响距离确定模型,以此将障碍物影响距离从传统势函数中的固定值改为实时根据障碍物碰撞危险度所确定的动态值;3)针对人工势场法存在的GNRON问题,根据造成该问题的障碍物特点,设计时间碰撞危险度评估模型;4)针对人工势场法在动态规划环境下存在的陷阱问题,根据该问题的特征,总结陷阱问题发生的条件,并采用虚拟障碍物的思想来阻止该问题的发生.

相比目前已有的采用人工势场法进行集群航路规划的方法,本文所提方法仍采用传统人工势场法的数学模型,仅从算法执行机制入手,克服人工势场法在集群航路规划上的不足,并使传统人工势场法的固有不足得到改善,极大程度的保留了人工势场法相比其他航路规划算法的最大优势,即算法数学描述简洁且易于执行.

2 航路规划算法

2.1 势函数模型

为了方便描述,本文将航路规划的对象统称为机器人,而不针对任何特定的机器人类型以及具体的应用场景.

人工势场法是将机器人在环境中的运动视为一种在虚拟人工受力场中的运动[26].障碍物产生的斥力与目标产生的引力共同决定机器人的运动.在动态环境下,即运动的目标和障碍物,其引力势能函数[29]如下:

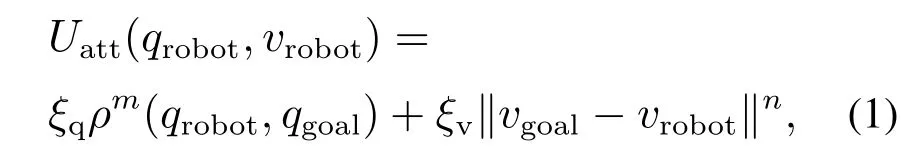
式中:qrobot和qgoal分别为机器人和目标的位置坐标;vrobot和vglobal分别为机器人和目标的速度;ρ(qrobot,qgoal)为机器人与目标之间的距离;‖vgoal−vrobot‖为机器人与目标之间相对速度的大小;ξq为受距离影响的引力场增益系数;ξv为受速度影响的引力场增益系数;m和n为正常数.当目标静止时,ξv为0,该引力势能函数就退化成传统的引力势能函数[26].对应的引力函数Fatt(qrobot,vrobot)为引力势能函数的负梯度.传统斥力势能函数[26]如下:

式中:η是斥力场增益系数;ρ(qrobot,qobs)是机器人到障碍物的最短距离;qobs是障碍物上的一个点,机器人到该点的距离是机器人到该障碍物的最短距离;ρ0是障碍物有效影响距离.对应的斥力函数Frep(qrobot)为斥力势能函数的负梯度.

2.2 障碍物影响距离

2.2.1 障碍物模型化

本文中,两个障碍物之间的距离默认可以安全通过一个机器人,若不能通过,则把这两个障碍物当成一个障碍物来处理.为了便于计算机器人与障碍物的最短距离,本文将障碍物用一个圆形区域包围,以此作为航路规划的障碍区.设qobstacle为障碍区中心位置坐标,Robstacle为障碍区半径,则qobs为

由于本文对障碍物采用圆形建模,机器人与障碍物的距离相比实际距离很可能偏小,故通过下文将介绍的碰撞危险度模型所解算出的障碍物碰撞危险度相比实际可能偏大,这在一定程度上会削弱避免无谓避碰行为的效果.因此,为了更好地避免无谓避碰行为的发生,在实际应用中,障碍物的建模应尽可能与障碍物本身相符.本文为了计算方便,对机器人同样采用圆形建模,由此式(1)中qrobot和qgoal则分别具体代表机器人中心的位置坐标和目标中心的位置坐标.

2.2.2 碰撞危险度模型

碰撞危险度分为空间碰撞危险度和时间碰撞危险度[31-32].空间碰撞危险度反映了碰撞的可能性大小,时间碰撞危险度是在有碰撞可能的情况下反映碰撞的紧迫程度.

1) 空间碰撞危险度.

空间碰撞危险度udT定义[32-33]为

式中:Dcpa为最近会遇距离;d1为最低安全会遇距离,d2为空间碰撞危险度零边界,通常d2≈2d1[32-33].

针对机器人与圆形障碍区的碰撞危险度解算,定义d1:指机器人边界与障碍区中心的最低安全会遇距离;定义d2:指空间碰撞危险度开始等于0时机器人边界与障碍区中心的会遇距离;定义dsafe:指机器人边界与障碍区边界的最低安全距离;定义Dcpa:指机器人与障碍区会遇时,机器人边界与障碍区中心最近的距离.因此最低安全会遇距离与空间碰撞危险度零边界为

式中:r为机器人的半径,其大小是机器人外形大小的一种抽象体现;Tcpa为最小会遇时间[32-33].

2) 时间碰撞危险度.

在进行航路规划中,机器人与目标的位置示意如图1[34]所示,图中各区域是相对于机器人当前位置而定的,即各区域的实际位置随着航路规划的不断进行而发生改变.

图1 GNRON问题位置分析Fig.1 Position analysis of the GNRON problem

由文献[34]的分析可知:1)对机器人有较高碰撞危险的障碍物即区域1内的障碍物和相对目标运动的障碍物,反而不容易造成GNRON问题,本研究称这类障碍物为第1类障碍物;2)容易造成GNRON 问题的障碍物即位于区域2和3内且相对于目标静止的障碍物,却对机器人没有较高的碰撞危险,本研究称这类障碍物为第2类障碍物.因此,时间碰撞危险度utT定义为

即针对第1类障碍物采用常规的时间碰撞危险度评估模型utT1[32-33],针对第2类障碍物采用特殊的时间碰撞危险度评估模型utT2.式中:vOG为障碍物相对于目标的速度;ρ(qrobot,qobstacle)为机器人中心与障碍区中心的距离;vOR为障碍物相对于机器人的航速;D1为最晚转向距离[33-34];D2为d2所对应的最晚转向距离,即通过将d1替换成d2而求得的“D1”,具体计算细节见文献[33].式(4)(8)以及式(9)中3.03的设置依据见文献[32].相比utT1,utT2的不同主要为:1)若障碍物位于区域3即ρ(qrobot,qobs)>La,则该障碍物的时间碰撞危险度直接为0;2)位于区域2的障碍物,只要机器人与该障碍物的最短会遇距离不小于最低安全会遇距离即|Dcpa|≥d1,则该障碍物的时间碰撞危险度也为0.

3) 碰撞危险度总模型.

碰撞危险度总模型uT为

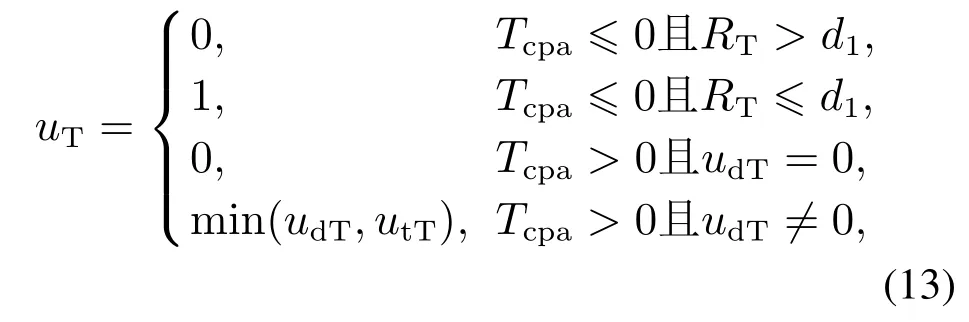
式中RT为机器人边界与障碍区中心的距离.

2.2.3 障碍物影响距离的确定

为了确保当机器人与障碍物存在碰撞危险时,机器人在该障碍物影响范围内,从而通过势函数法采取相应的避碰措施,障碍物的ρ0为

式中λ为大于1的数.

2.3 陷阱问题

2.3.1 陷阱问题的分析

陷阱问题是局部极小值问题在动态环境下的表现形式[34],主要包括某区域内持续徘徊甚至静止不动、抖动性远离目标以及抖动性接近目标.根据文献[34]的研究结果,当存在障碍物在机器人的运动方向上且机器人继续保持该运动方向时:1) 若障碍物静止,则机器人很可能在某区域内持续徘徊;2)若障碍物与机器人相向而行,则机器人很可能抖动性远离目标;3)若障碍物与机器人同向而行且机器人存在追越障碍物的可能,则机器人很可能抖动性接近目标.

由于势函数法是目标导向性的[25,34],故在判断算法执行是否可能发生陷阱问题时,仅考虑目标引力对机器人运动的影响.陷阱问题的发生需要机器人保持一个运动方向不变,在不考虑障碍物影响的情况下,当目标为静止时,只要目标在机器人的运动方向上,则机器人就可以保持运动方向不变,当目标为运动时,仅当目标在机器人的运动方向上且机器人对目标的Dcpa=0,机器人才能保持运动方向不变.陷阱问题的实质是机器人对障碍物采取的必要避碰行为,但由于势函数法自身的问题,机器人的避碰并不是有效的,而机器人对障碍物进行避碰则表明该障碍物对机器人的碰撞危险度uT>0.

综上所述,若同时满足:1)θG=0◦且机器人对目标的Dcpa=0,这里θG为目标相对于机器人运动方向,顺时针计量的方位角度,即船舶领域中的舷角[32-33];2)障碍物对机器人的Dcpa=0且Tcpa>0;3)障碍物为静止的或障碍物的航向与机器人的航向在同一条直线上;4)障碍物对机器人的碰撞危险度uT>0,则航路规划很有可能出现陷阱问题.

2.3.2 虚拟障碍物

由陷阱问题发生的条件不难知道:qgoal,qobs和qrobot三点共线是陷阱问题发生的必要条件.因此,只要使得这三点不共线,陷阱问题就可以得到解决.

本文引入虚拟障碍物法,当航路规划同时满足陷阱问题发生的4个条件时,在机器人附近设置一个质点型虚拟障碍物,它对机器人施加一个附加斥力,使得在接下来的航路规划中qgoal,qobs和qrobot三点不再共线.为了防止所放置的虚拟障碍物增加陷阱问题发生的可能,附加斥力垂直于三点的连线[16,28]且指向障碍物较稀疏的方向[14,16].为了有效的破坏陷阱问题发生的必要条件,本文将虚拟障碍物与机器人中心的距离设为机器人的半径r,虚拟障碍物的ρ0为一个默认值,即不通过碰撞危险度来确定.

3 二重势能场

3.1 问题描述

在给定集群构型的情况下,对集群进行航路规划,需完成的4点功能按优先级由高到底排序为:1)集群单元的避障以及单元间的避碰;2)集群到达目标位置;3)构型的形成;4)构型的保持.功能3)和4)分开列出的原因为集群行动时会根据实时态势以及任务需要对构型进行调整,若此时集群已经形成原规划的构型并保持,则停止保持该构型,而以新规划的构型为准并形成.

为实现上述功能,本研究采用如图2的航路规划方式.

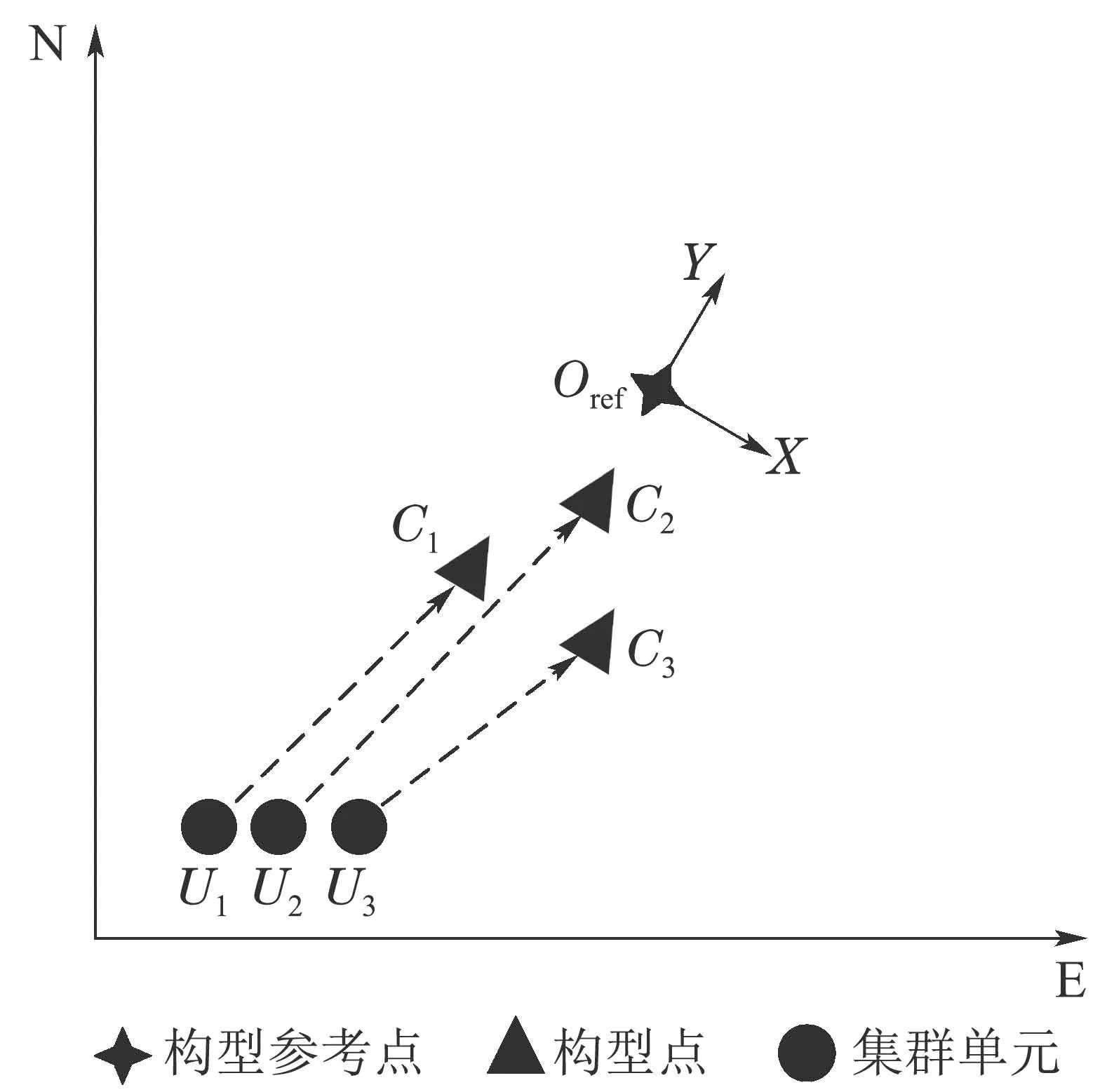
图2 集群航路规划示意图Fig.2 Schematic diagram of cluster route planning

根据给定的集群构型选择合适的构型参考点Oref,并将Oref放置在合适的初始位置.在集群构型不变的情况下,各个构型点Ci相对于Oref的位置始终不变.通过对Oref进行航路规划,得到Oref从初始位置到目标的航路,并实时根据Oref位置的变化确定Ci的位置.集群各单元Ui以对应的Ci为动态目标,进行航路规划.由于本文的研究重点是集群的航路规划,故集群构型的确定、构型参考点的选择及其初始位置的确定不在本研究的范围之内.

根据本研究中碰撞危险度模型以及人工势场法的特点,本文以正北方向为Y轴,正东方向为X轴,建立大地坐标系,坐标系的原点根据规划空间的具体情况来选定,大地坐标系中所有角度按正北方向顺时针计量.根据本研究中集群航路规划的特点,本文以构型参考点的位置为坐标原点,其运动方向为Y轴指向,X轴指向为Y轴指向顺时针旋转90◦所得,建立构型参考点的随体坐标系,在该坐标系下,所有角度按Y轴指向顺时针计量.

3.2 第一重势能场

第一重势能场的作用:通过对构型参考点建立第一重势能场,规划出构型参考点到目标的航路,以此根据构型参考点在航路中的实时位置,解算出各个构型点的实时位置.

第一重势能场所面对的目标是根据集群的实际目标所选取的目标点,该目标点的选取既要考虑集群的任务类型,又要考虑构型参考点相对于集群构型的位置情况.例如,集群的任务是到达一个指定区域,则构型参考点到达所选取的目标点时,集群的各构型点均要在该指定区域内.再如,集群的任务是跟踪某一目标,则构型参考点到达所选取的目标点时,集群各单元在对应的构型点上可以保证整个集群对目标可观测且与目标保持一定距离.

在不考虑目标点具体选取细节的情况下,构型参考点的任务简单地说就是到达目标点.目标点的状态可分为静止和运动,而构型参考点对目标点所采用的到达方式分为“软着陆”和“硬着陆”.对于静止的目标点,构型参考点采用“硬着陆”方式,即ξv=0;对于运动的目标点,构型参考点通常采用“软着陆”方式,即ξv0.

第一重势能场为第二重势能场提供各构型点在大地坐标系下实时的位置以及速度.设构型参考点在大地坐标系下的位置坐标为(xrefyref)T,速度为(vxrefvyref)T;设构型点在构型参考点随体坐标系下的位置坐标为(xRCyRC)T;设构型点在大地坐标系下的位置坐标为(xCyC)T,速度为(vxCvyC)T,则有

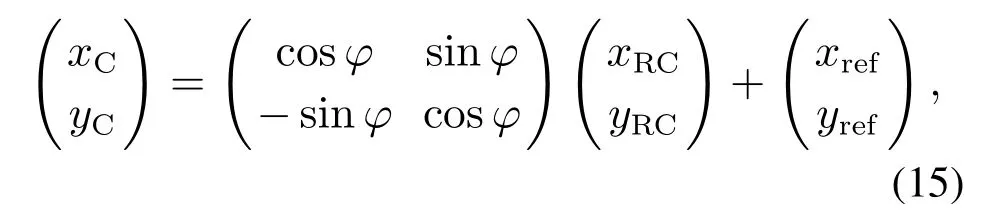
3.3 第二重势能场

第二重势能场的作用:将第一重势能场所提供的构型点作为集群中对应单元的动态目标点,通过对集群各单元建立第二重势能场,以此规划出集群各单元到对应构型点的跟随路径,从而完成整个集群的航路规划.

从集群航路规划需完成第3.1节所提的4个功能上看,第一重势能场主要是完成功能2),第二重势能场主要是完成功能1),3)和4),而集群单元对构型点的跟随直接完成功能3)和4),即构型形成与保持,因此集群单元对构型点采用“软着陆”到达方式.

第二重势能场需要完成集群中各单元间的避碰,对某一个单元进行航路规划时,需要考虑集群中其他单元的速度以及运动方向,而其他单元的速度以及运动方向同样也是通过航路规划所得,即存在集群单元间运动状态相互影响的问题,这就使得第二重势能场不易于实现集群单元间避碰的功能.对此,本文采用避碰优先级的处理方式.首先,对集群中各单元进行避碰优先级的评定并排序;然后,按照避碰优先级由高到低的顺序对集群单元进行航路规划.对集群单元进行航路规划时,仅需考虑对避碰优先级高的单元进行避碰.而避碰优先级的评定与具体任务类型、集群单元属性以及集群态势变化等因素有关,故不在本研究范围内.

由于在第一重势能场中,航路规划的对象仅为构型参考点,且规划过程并不考虑各构型点的位置.因此,根据构型参考点实时位置所确定的构型点有可能会在障碍区内,这样的构型点显然是不可安全跟随的,若集群中对应的单元以该构型点为目标,则存在碰撞的危险.对于这种情况,本研究采取的解决方法是:当集群单元所对应的构型点在障碍区内,则该单元以避碰优先级比其高一级的集群单元为目标进行航路规划,且速度大小与高一级单元保持一致,对于避碰优先级最高的单元,其高一级单元为构型参考点,此外,对应的构型点作为第一重势能场中的障碍物,参与接下来的航路规划,其uT设置为1,直至对应构型点离开障碍区.

由于第二重势能场所要完成的功能中优先级最高的是功能1),因此只有构型点不在障碍区内,且可以安全跟随,则对应的集群单元以该构型点为目标,否则以高一级单元为目标.判断构型点是否可安全跟随的方法为:若所有实际障碍物对构型点的合斥力为0,则该构型点可安全跟随.

4 集群航路规划总模型

将航路规划算法与二重势能场思想相结合,形成集群航路规划总模型,其模型的总流程如图3 所示(图3见下一页).

首先判断整个集群是否达到目标位置,即在构型参考点到达目标点的情况下,集群各单元到达对应构型点位置,若到达,且对于动态目标,在不需要继续跟随目标的情况下,结束集群航路规划,否则继续进行接下来的规划过程.

图3中的子流程为航路规划算法的流程,如图4所示.

由于航路规划的目的是让机器人在不与障碍物发生碰撞的情况下尽快到达目标,即航路规划具有目标导向性[25,34],因此在进行碰撞危险度解算,以及判断是否满足陷阱问题发生条件的过程中,以目标引力的方向为机器人速度方向,且机器人速度大小不变.基于碰撞危险度确定障碍物的影响距离后,判断是否满足陷阱问题发生的条件,若满足则进行虚拟障碍物的放置并进行航路规划,否则直接进行航路规划.航路规划后,若放置了虚拟障碍物则撤除所放置的虚拟障碍物.

图3中所涉及的初始化设置如图5所示.在整个集群航路规划的过程中,集群单元航路规划的情况,如集群单元与对应构型点的距离,可能会影响集群单元的避碰优先级.因此,在集群航路规划过程中,集群单元的避碰优先级可能要实时进行调整.此外,在集群航路规划过程中,也可能进行集群构型的调整.但由于本研究不涉及这些,故在总流程中未标出.

图3 算法总流程Fig.3 Total algorithm flow

图5 初始化设置Fig.5 Initial setting

图4 子流程Fig.4 Sub process

5 想定验证

引力势函数模型中参数设定为m=n=2,ξq=0.1,ξv=0.05;斥力势函数模型中参数设定为η=0.3,ρ0默认为2 m(传统方法和虚拟障碍物使用);障碍物影响距离确定模型中参数设定为λ=2.为便于仿真,不考虑实际动态障碍物的半径.

5.1 单机航路规划

为了验证本文所提出的势函数法在陷阱问题、无谓避碰问题以及GNRON问题上的处理能力,设置单机航路规划仿真实验.假设机器人以恒定速度移动,虚拟力仅改变其运动方向.机器人参数设定为:半径r=0.15 m,机器人速度vrobot=0.2 m/s.

5.1.1 陷阱问题

以抖动性远离目标为例,在一个开放空间中,机器人出发位置为(0,0)m;目标静止,其位置为(10,10)m;设置障碍物:位置为(5.5,5.5)m,速度为0.15m/s,航向为225◦.

分别采用传统的人工势场法和本文改进的人工势场法进行单机航路规划.见图6,当采用传统人工势场法时,由于陷阱问题的发生,机器人抖动性远离目标.

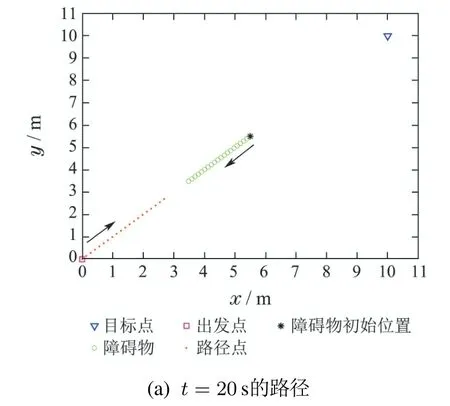
图6 抖动性远离目标Fig.6 Jittering away from the goal

如图7所示,当采用本文改进的人工势场法时,由于满足陷阱问题发生的条件,因此机器人在虚拟障碍物的斥力作用下不再与障碍物和目标三点共线,从而避免了陷阱问题的发生.

图7 避免抖动性远离目标Fig.7 Avoid the problem of jittering away from the goal

5.1.2 无谓避碰问题

参照文献[34],设置动态仿真环境.动态目标初始位置为(10,10)m,其速度为0.112 m/s,航向为116.56◦.初始化6个动态障碍物:Obs 1位置为(5,0)m,速度为0.12 m/s,航向为0◦;Obs 2位置为(9.4,4.8)m,速度为0.29 m/s,航向为270◦;Obs 3位置为(19,10)m,速度为0.082 m/s,航向为218◦;Obs 4 位置为(10,0)m,速度为0.3 m/s,航向为315◦;Obs 5位置为(15,12)m,速度为0.085 m/s,航向为180◦;Obs 6位置为(0,3)m,速度为0.13 m/s,航向为45◦,加速度为0.002 m/s2,加速度方向为90◦.放置8 个静态障碍物:Obs 7位置为(6.5,10.5)m,半径为0.7 m;Obs 8 位置为(17.8,4.3)m,半径为1.05 m;Obs 9 位置为(20,7)m,半径为1.05 m;Obs 10 位置为(11,5.35)m,半径为0.5 m;Obs 11位置为(10.5,7.5)m,半径为0.5 m;Obs 12位置为(3,3.6)m,半径为0.3 m;Obs 13 位置为(7.3,3.95)m,半径为0.35 m;Obs 14位置为(10.5,10.5)m,半径为0.4 m.机器人出发位置为(0,0)m.

分别采用传统的人工势场法和本文改进的人工势场法进行单机航路规划,如图8和图9所示.

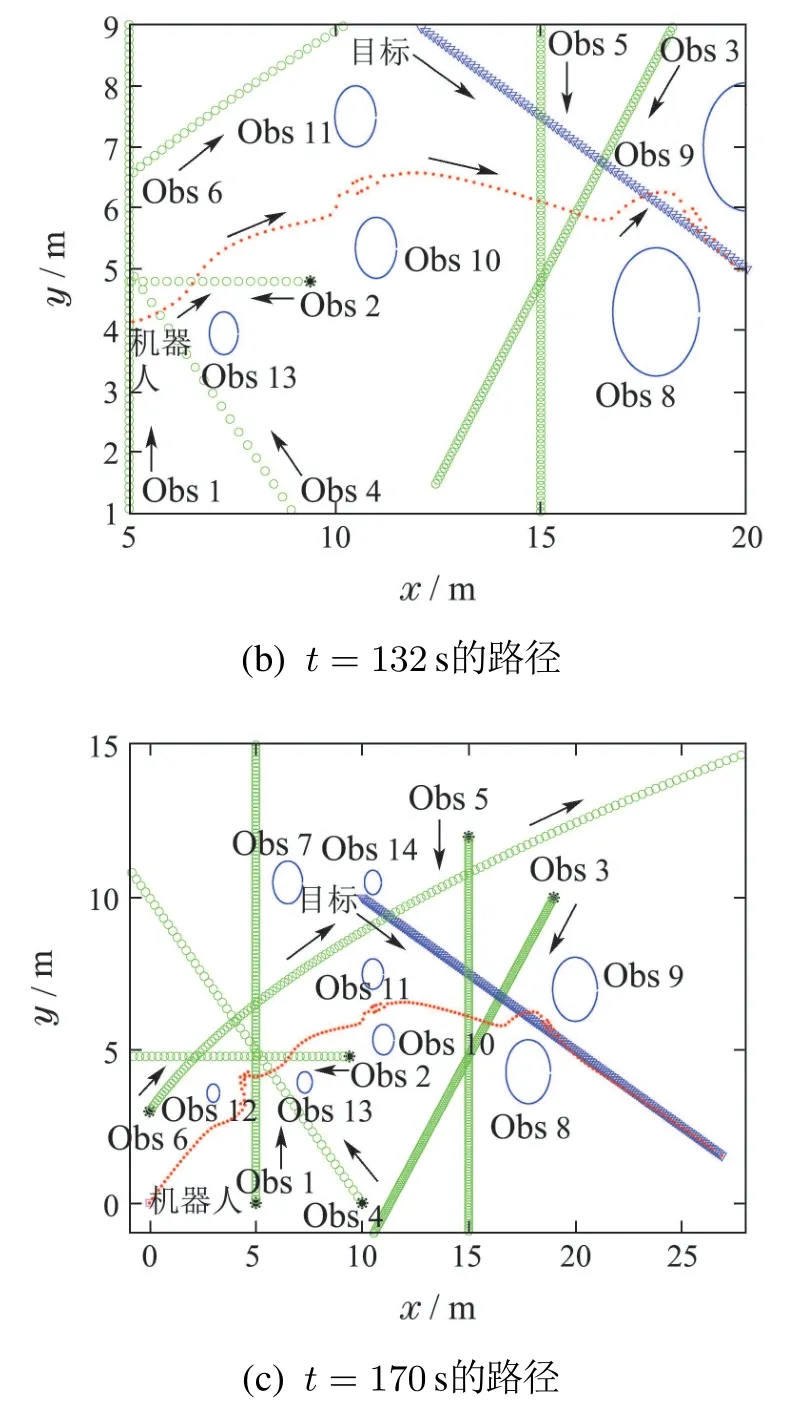
图8 无谓避碰Fig.8 Unnecessary collision avoidance

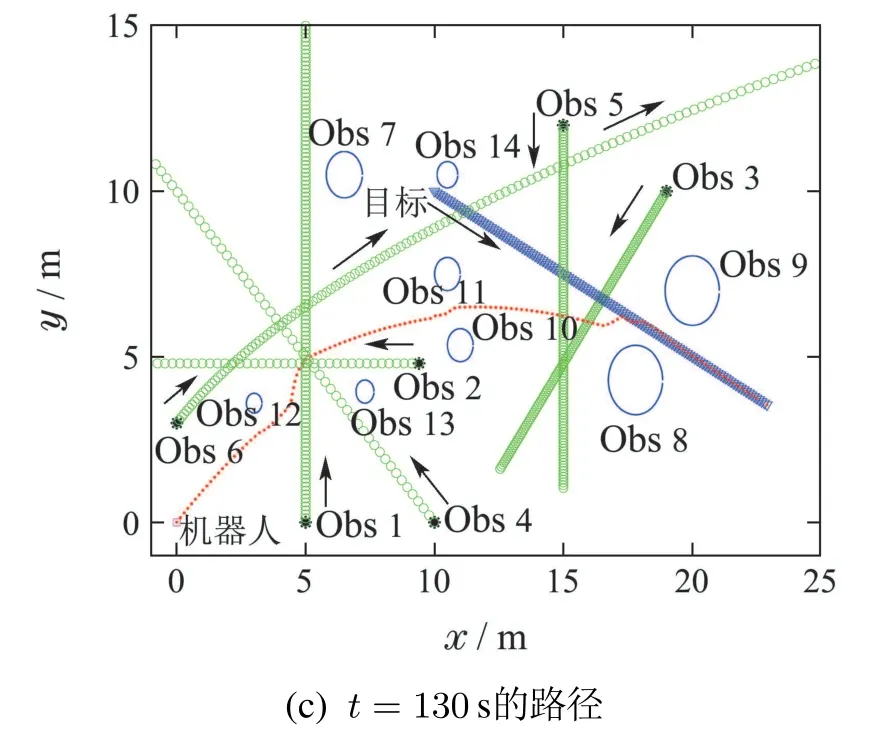
图9 避免无谓避碰Fig.9 Avoid the problem of unnecessary collision avoidance

由图8(a)和图9(a)可知,相比传统方法,本文方法使机器人在经过Obs 12附近和与Obs 1会遇的过程中很好的避免了无谓避碰行为,确保机器人能够抓住时机直接从Obs 1前横越过去.由图8(b)和图9(b)可知,相比传统方法,由于本文方法能够很好的避免无谓避碰行为,故机器人在通过Obs 10与Obs 11之间和Obs 8与Obs 9之间时,路径相对平滑,不存在路径点抖动问题.相比传统势函数法用170 s到达目标,本文所提方法仅用130 s.

5.1.3 GNRON问题

在与第5.1.2节相同的仿真环境下,将动态目标改为静态目标,分别采用传统的人工势场法和本文改进的人工势场法进行单机航路规划.如图10所示,当采用传统方法时,由于Obs 14在目标附近,导致GNRON问题的发生,使得机器人无法到达目标.如图11所示,当采用本文方法时,由于时间碰撞危险度评估模型对障碍物进行有区别的评估,从而屏蔽了Obs 14对机器人的影响,避免了GNRON问题的发生,机器人顺利到达目标.

图10 GNRON问题Fig.10 The problem of GNRON

图11 克服GNRON问题Fig.11 Overcome the problem of GNRON

5.2 集群航路规划

对于集群来说,静态目标可以看作是将动态目标的速度设为0,因此集群以指定构型追上并跟随动态目标更具有一般性.现设置想定:5个运动单元组成一个集群,集群以集群外的一个单元为领航者,形成指定构型,当构型形成时,在领航者的随体坐标系中,单元U1位置为(−0.5,−0.866)m,单元U2位置为(0.5,−0.866)m,单元U3位置为(1,−1.7321)m,单元U4位置为(0,−1.7321)m,单元U5位置为(−1,−1.7321)m.集群各单元与领航者半径r均为0.1 m,速度最大为0.2 m/s,领航者初始化数据与第5.1.2节的动态目标相同.

当采用文献[6]中的方法时,由于不考虑集群单元的具体类型,因此不涉及文献[6]中的目标跟踪算法,则集群单元可视为文献[6]中的虚拟结构质点,以领航者为编队参考点,并设置虚拟结构,通过传统人工势场法形成队形.集群单元间用于避碰的ρ0为0.4 m.

当采用本文所提的集群航路规划法时,则将领航者视为目标,想定转变为:集群以没有领航者的非完整构型,追上并跟随领航者.集群单元避碰优先级的关系设为:U1>U2>U3>U4>U5,构型参考点的速度恒为0.175 m/s.

5.2.1 无障碍物环境

在无障碍环境下,初始化5 个集群单元的位置:U1为(0,0.5)m,U2为(0.5,0)m,U3为(1,0)m,U4为(0,0)m,U5为(0,1)m.现分别采用文献[6]的方法与本文的方法,当采用本文的方法时,构型参考点的位置初始化为(2,2)m,仿真结果如图12和图13所示.

如图12所示,当采用文献[6]方法时,由于集群单元各自为政,单元路径发生非必要交错,加剧碰撞发生的可能性,从而出现由避碰所产生的明显避碰路径;且由于集群单元间无避碰优先级之分,因此采取避碰措施的单元并非一个;此外,由于避碰仅考虑距离因素,避碰路径较为抖动.

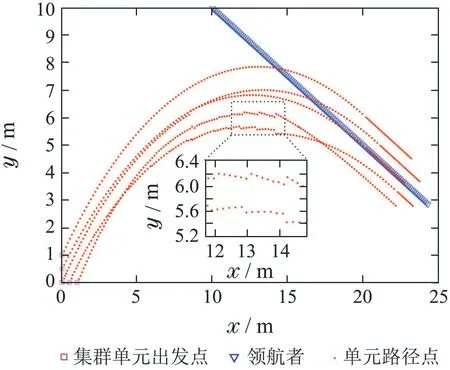
图12 无障碍环境下采用文献[6]方法Fig.12 The method of reference [6]used in no-obstacle environment

相比之下,如图13所示,当采用本文方法时,由于第二重势能场的作用,使集群单元的行动从一开始就受到了约束与引导,避免了单元路径非必要交错,各单元各行其道,在83 s时形成无领航者的非完整构型,并以该构型继续前进,直到与领航者形成完整构型,相比文献[6]方法用时144 s,本文方法用时131 s.

图13 无障碍环境下采用本文方法Fig.13 The proposed method used in no-obstacle environment

5.2.2 多障碍物环境

现设置障碍物初始化数据与第5.1.2 节相同,在该多障碍物环境下,初始化5 个集群单元的位置:U1为(−1.26,−0.76)m,U2为(−1.76,−0.76)m,U3为(−2.26,−0.76)m,U4为(−2.76,−0.76)m,U5为(−3.26,−0.76)m.现分别采用文献[6]的方法与本文的方法,当采用本文的方法时,构型参考点的位置初始化为(0,0)m,仿真结果如图14和图15所示.

图14 多障碍环境下采用文献[6]方法Fig.14 The method of reference [6]used in multi-obstacle environment

图15 多障碍环境下采用本文方法Fig.15 The proposed method used in multi-obstacle environment

当采用本文方法时,集群各单元从行动开始就试图组成无领航者的非完整构型.如图15(a),集群单元开始就散开试图组成非完整构型,虽然由于障碍物的威胁,集群不得不暂时收拢,但集群通过Obs 12 与Obs 13后就重新散开进行尝试;再如图15(b),集群通过Obs 10与Obs 11后,又重新散开试图组成非完整构型.由图15(c)和图15(d)可知,由于障碍物较多,集群未能在与领航者组成完整构型前形成非完整构型,但对比图14,正因为这种贯穿始终的“试图”,使得集群单元以一个整体的姿态行动,再加上依据障碍物碰撞危险度进行避障,以及集群单元间依据避碰优先级有差别避让,很好地提高了行动效率,相比文献[6]方法用230 s形成构型,本文方法用了172 s.

6 结论

针对人工势场法在集群航路规划中构型组织能力的不足,提出基于二重势函数法的集群航路规划法,通过第一重势能场形成集群到目标的可行路径,第二重势能场形成集群构型,从而实现集群的航路规划.此外,针对避障过程中人工势场法仅考虑距离因素而导致无谓避碰现象的发生,引入碰撞危险度评估模型,根据障碍物的碰撞危险度来确定障碍物影响距离,以此避免无谓避碰现象的发生;针对人工势场法在航路规划中存在的GNRON问题,通过引入两种时间碰撞危险度评估模型,实现对障碍物有区别的评估,从而克服GNORN问题;针对人工势场法存在的陷阱问题,通过引入虚拟障碍物予以避免.MATLAB仿真结果证明了所提的改进人工势场法以及以该人工势场法所构成集群航路规划法的可行性.

基于二重势函数法的集群航路规划法为采用人工势场法实现集群航路规划提供了一种思路,其中一些本文未过多涉及的点,如集群构型的确定、构型参考点的确定和初始位置的选择、集群单元避碰优先级的设定以及实时调整等,同样也举足轻重,需要进一步去研究.