船舶航向保持运动的间接自回归历遍模型建模

卢秋铸吴 军陈佰健杨 鑫

(1.长沙理工大学电气与信息工程学院,湖南长沙 410114;2.中国测试技术研究院,四川成都 610021)

1 引言

对于船舶运动学模型的研究,国内外已经有长久的研究历史,并取得了丰富的研究成果.现在广泛使用的船舶模型大致可分为以Abkowitz方程为代表的“整体型”[1]和以机动建模组(maneuvering modeling group,MMG)方程为代表的“分离型”两大类.建模需要精确的船舶自身物理参数以及作用于船舶的力学参数,其中船体、螺旋桨和船舵等的受力相互耦合,因此MMG模型的建立难度比较大.

国内对船舶MMG模型也有较多的研究[2],文献[3]介绍了用MMG标准方法建立的船舶操纵模型,但是对于船舶这种复杂的被控对象,船舶推进系统的时变不确定度,几何尺寸的不确定性以及力学参数的不确定度,使得物理模型的建立相当困难[4].辨识建模是使用辨识算法拟合试验数据,并兼顾模型泛化能力的建模方法[5].将船舶视为一个“黑箱”系统,进行合理的船舶操舵实验,得到输入输出数据,并以数据驱动辨识得到船舶操纵模型.

近年来国内在船舶的连续模型辨识建模方面也有很多研究成果,文献[6]提供了一种使用模糊神经网络辨识建模的方法,实现在复杂水动力导数和强烈不确定性下的动力学建模,但是训练中的仿真数据可能与船舶实际物理特性不符.文献[7]应用最小二乘支持向量回归机辨识船舶操纵运动模型参数,以Z形实验数据进行参数识别与检验.但是核函数的选取依靠人为经验,且带有一定的随意性.

在船舶的离散模型建模研究方面,Ohtsu等人[8-9]将统计建模法应用于“汐路丸”船舶建模,尝试用线性自回归历遍(auto-regresive eXogenous,ARX)模型来描述船舶的艏摇角和舵角间的动态特性,并基于极大似然估计辨识模型参数,采用赤池信息准则(Akaike information criterion,AIC)确定模型阶次.在后续的研究中,Peng和Wu等人[10-11]在原有的ARX模型结构中入了偏移项,并采用径向基(radial basis function,RBF)神经网络辨识仿射结构ARX模型的函数型系数,得到了全局时变非线性、局部线性的RBF-ARX 模型,来描述“汐路丸”艏摇角和舵角之间的动态关系.

但是RBF-ARX模型本身结构复杂,参数较多,辨识过程比较难懂[12].近年来对ARX模型有了更深入的研究,在文献[13]中表示高阶ARX模型可以近似表达一般普遍的线性系统,并且在此基础上说明了在系统具有不稳定极点时,高阶ARX模型仍然适合对该系统进行一贯地建模.

Ohtsu和Peng的研究目的是设计基于模型的最优控制策略,仅用一步预测误差和控制的有效性来检验模型性能,没有考虑模型的长期预测性能,也没有与MMG模型进行对比.另外,直接以船舶舵角和艏摇角偏差为输入输出构建的ARX结构的模型,只考虑到输入输出简单的时间序列关系,而忽略了输出的变化率因素造成的影响,这使得长期预测误差不断累积,所建立模型有一定局限性.

因此,本文提出先以舵角和艏摇角偏差变化率为输入输出数据建立一个过渡模型,再利用艏摇角偏差与其变化率之间的差分关系,将模型参数还原为舵角和艏摇角偏差之间的映射关系.通过MATLAB仿真分析可以看出,本文间接建立的船舶ARX模型的预测效果优于直接建立的ARX模型,能够更好的体现船舶的运动特性,长期预测效果与广泛使用的MMG模型相当.

2 船舶直接ARX辨识模型

2.1 ARX模型

ARX是时序分析法中具有代表性的方法,其中ARX模型可以用于“黑箱”模型的建模,可适用于线性系统和非线性系统模型辨识.该模型在自回归(auto-regressive,AR)模型基础上,将控制因素引入系统作为外生变量(eXogenous),用于描述系统输入输出之间的映射关系,广泛应用于系统的建模与控制器设计和仿真.单变量仿射ARX模型一般可表示为

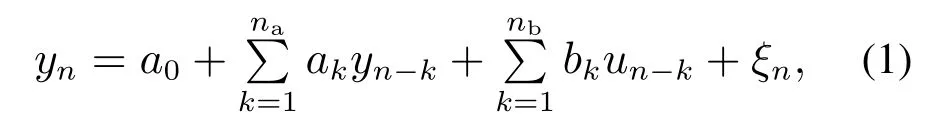
式中:un为输入量;yn为输出量;ξn为建模误差;ak(k=1,2,···,na),bk(k=1,2,···,nb)为自回归系数;na,nb为模型阶次;a0是偏移项.

直接建模的方法是将船舶艏摇角偏差作为输出,舵角为输入,建立单输入单输出的辨识模型:

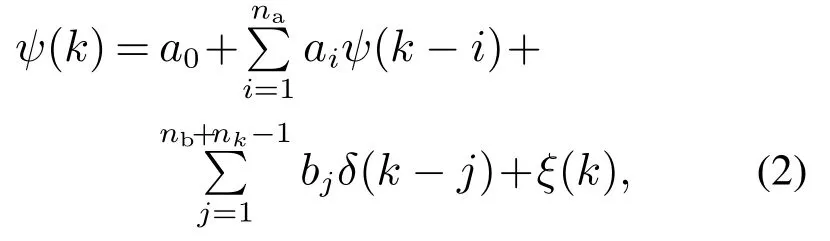
式中:ψ(k)是艏摇角偏差;δ(k)是舵角;ξk是白噪声信号;na,nb+nk−1为模型阶次;nk是系统延迟;a0是偏移量常数;ai和bj是ARX模型线性参数.

选择合适的真实航行数据对于建模也至关重要,建模数据直接影响数据驱动模型的预测精确度,研究所采用的舵角和航向角偏差数据由日本东京海洋大学的大津皓平教授提供,实验对象是东京海洋大学的训练船舶“汐路丸”,其主要参数如表1所示.

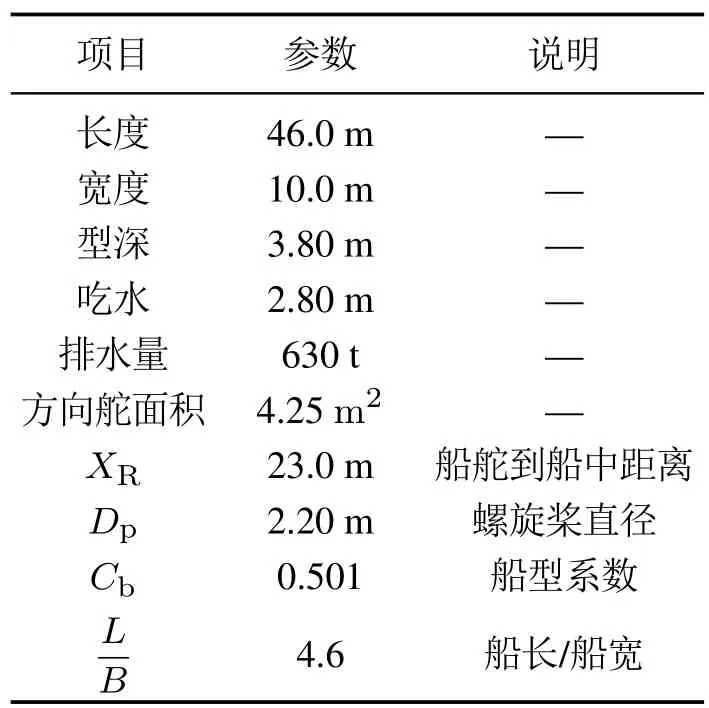
表1 汐路丸主要参数Table 1 Main parameters of the ship“Shioji-Maru”

建模数据共有4组,采样周期均为1 s,如图1所示为其中之一,这4组建模数据从特定的开环激励实验数据中挑选而得,具有一定的代表性,以满足建模的需要,其舵角都在大范围内剧烈变化,尽可能地包含了“汐路丸”的各种动态性能.

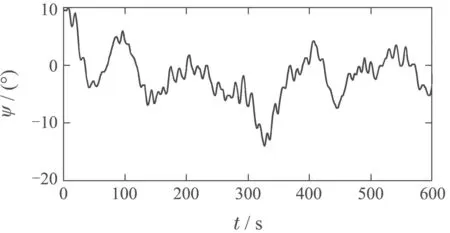
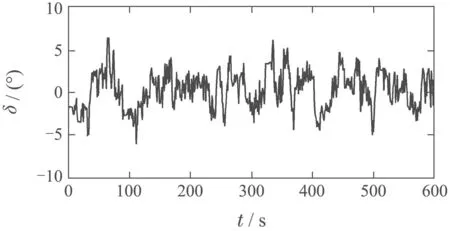
图1 “汐路丸”号真实航行数据Fig.1 “Shioji-Maru”actual sampling data

2.2 模型参数的辨识

根据式(2),可以将建模模型表示为

式中:Ψ为n×1维向量,表示n个采样时刻下的艏摇角偏差;X为n×(na+nb+nk)维矩阵;Θ为待求的模型参数;ξ为白噪声建模误差.

参数辩识的方法很多,如最小二乘法、极大似然法、贝叶斯法等.其中最小二乘参数辨识法是目前辨识方法中最普遍的一种,且很多辨识方法是基于最小二乘法的.最小二乘法的思想是找到使得辨识模型输出和真实输出之间误差平方和最小的一组模型参数.现定义损失函数为

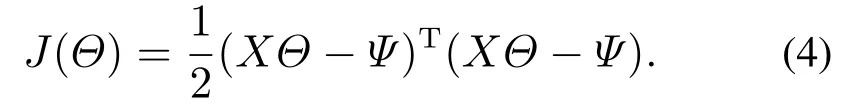
根据最小二乘法的思想,得到使得J(Θ)最小时的Θ即为所求模型参数,因此就该损失函数对Θ求导取0得

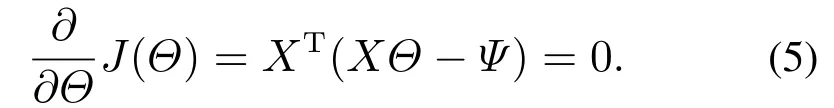
整理后即可得到XTΨ=XTXΘ,那么在XTX为非奇异矩阵时,存在(XTX)−1,可得模型参数

该方法简洁高效,但是依赖于XTX的可逆性,若XTX不可逆则需要对建模数据进行整理,去除掉冗余特征,使得|XT0再继续使用最小二乘法.

2.3 模型阶次的选择

建模过程中增加模型阶次可以提高模型精度,但是模型复杂度会增大,并易于导致过拟合问题.为此,采用信息准则作为确定模型阶数的依据.信息准则通过加入模型复杂度的惩罚项来避免模型过拟合问题,最常用信息准则为AIC准则,AIC准则即赤池信息量准则,赤池建议即当欲从一组可供选择的模型中选择1个最佳模型时,AIC值为最小的模型是最佳的[14].AIC计算公式为

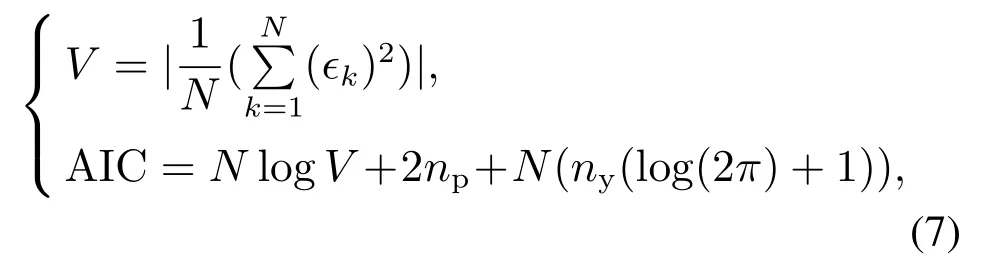
式中:V是损失函数;N是估计数据集中的数据个数,即用于建模的数据个数;ϵk=ψk−为模型预测误差,该处表示艏摇角偏差的预测误差;θn是模型参数;np是模型参数个数;ny是模型输出个数.

在船舶的建模中一般所选择的阶次不会太高,故将na,nb的上限定为20,nk为5.从1～20和1～5进行遍历建模,在不同的阶次下,分别求出辨识模型的AIC值,最终选择其值最小下的一组na,nb和nk作为船舶最优的模型阶次.现以建模数据1为例,在nk选择1的情况下,得到模型阶次na,nb在1～20遍历下的AIC三维图,如图2所示.

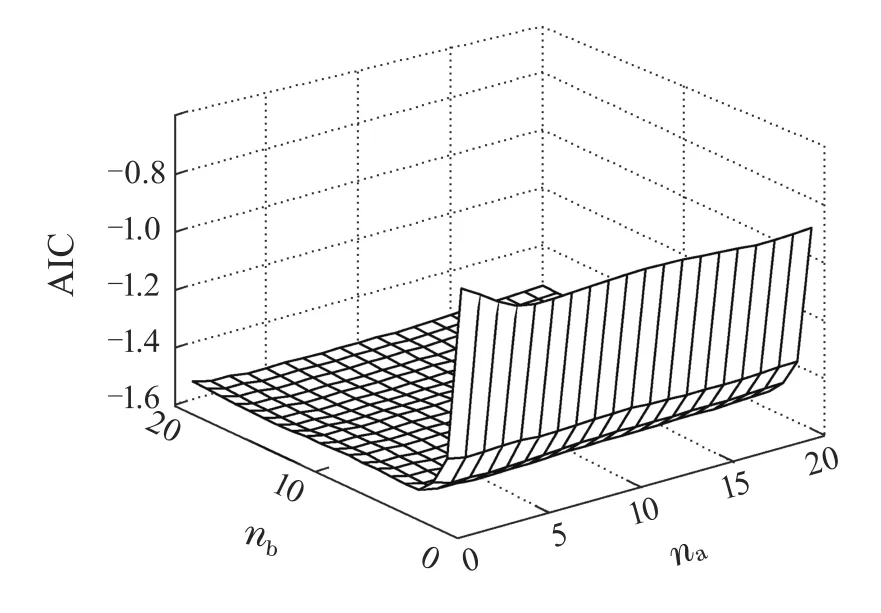
图2 直接模型AIC三维图Fig.2 AIC value of the direct model

得到的模型阶次为na=15,nb=4,并将此模型编号为模型1.对模型1进行残差分析可得图3,由图可知模型残差很小并且服从正态分布.

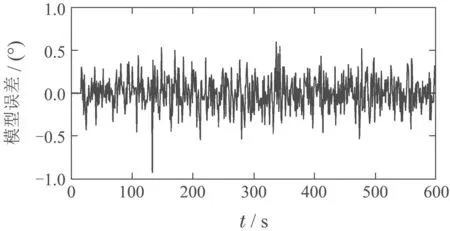
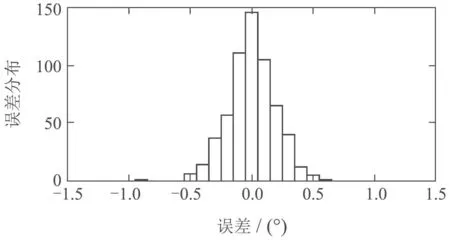
图3 直接模型1残差分布Fig.3 Direct Model 1 residual distribution

用同样的方法将另外3 组数据建模可以得到模型2、模型3以及模型4,模型残差均服从正态分布.

3 船舶间接ARX辨识模型

间接ARX辨识建模的方法是在原方法上的一种改进,采用的输出数据为船舶艏摇角偏差变化率∆ψ,输入数据仍然是舵角,建立单输入单输出的ARX模型:

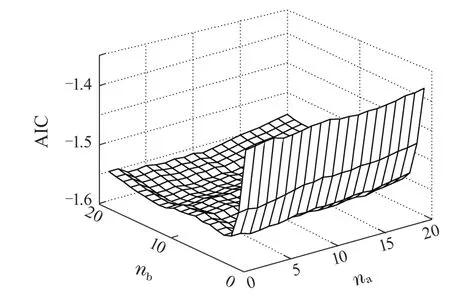
图4 间接模型AIC图Fig.4 AIC value of the indirect model

同样将该模型记为模型1,由图5得该模型建模残差服从正态分布.对其它3组航行数据用相同的方式进行建模,分别得模型2、模型3以及模型4,模型残差同样为正态分布.序号顺序和其对应的建模数据与直接建模下的保持一致.

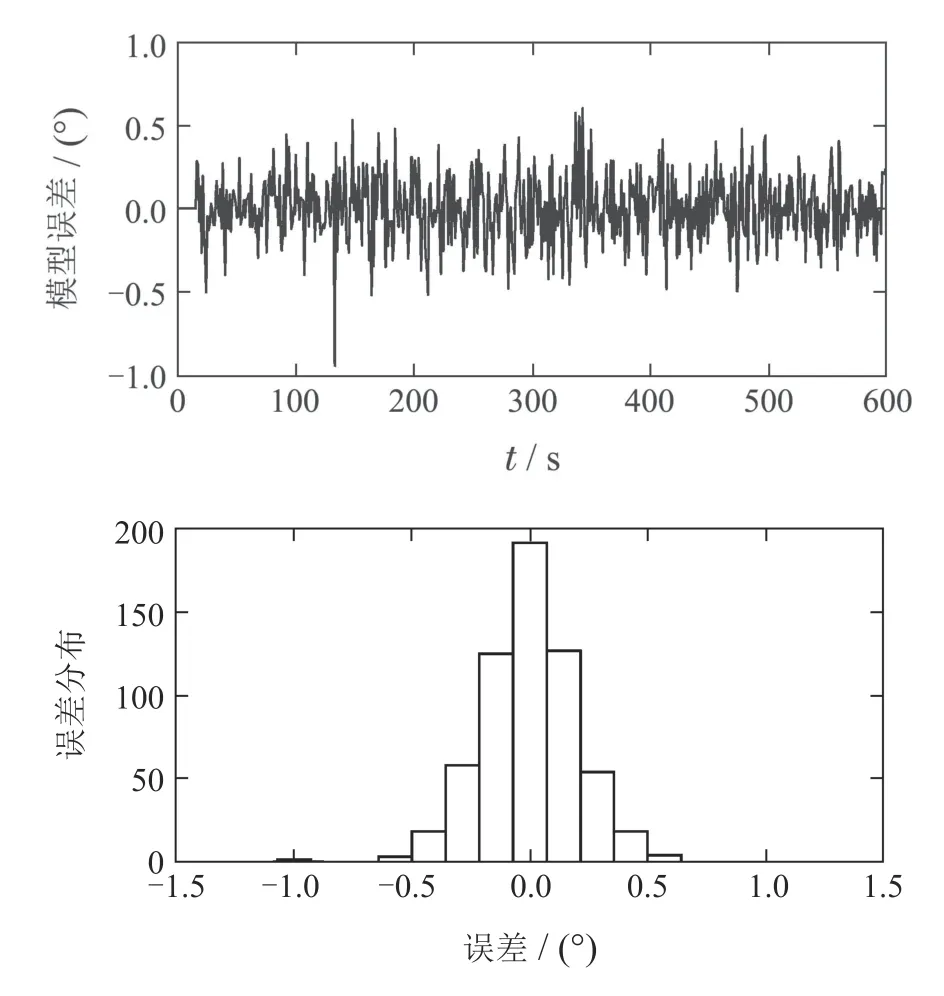
图5 间接模型1残差分布Fig.5 Indirect Model 1 residual distribution

4 模型的检验

4.1 模型AIC值

单纯观察两种建模方式的AIC值,直接建模和间接建模相差仅在0.01左右,几乎无差,见表2.况且衡量模型好坏的标准不能仅仅比较AIC值大小,还需要综合更多其它的因素,那么作为预测模型的ARX模型,一步预测和长期预测精度就非常重要.

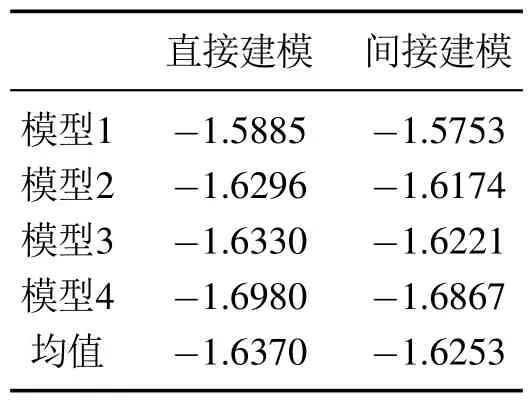
表2 AIC值Table 2 AIC value

4.2 ARX模型的检验

船舶航行实验中还记录了5组数据用于模型的检测,测试模型的预测性能,如图6-10所示.

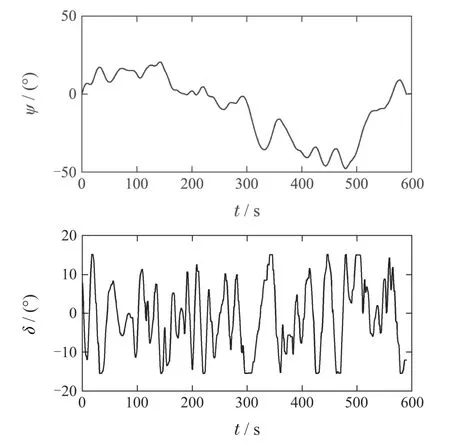
图6 测试数据1Fig.6 Test data 1

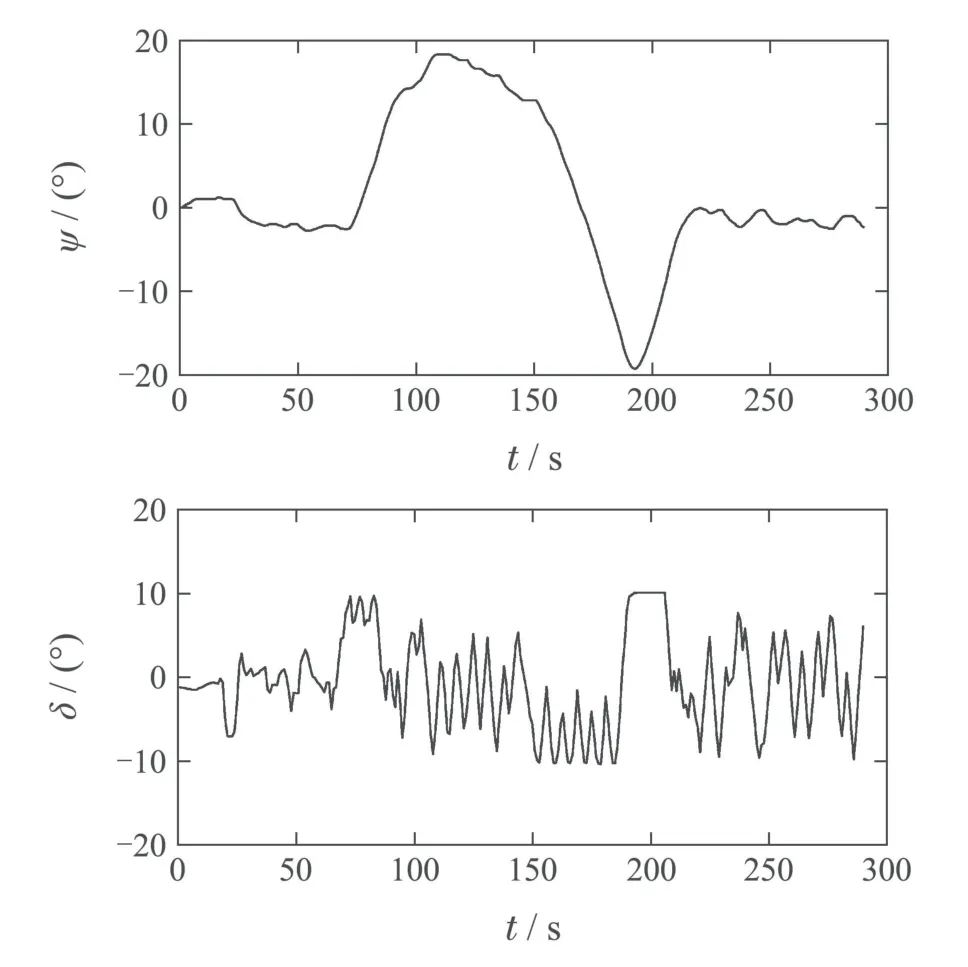
图7 测试数据2Fig.7 Test data 2

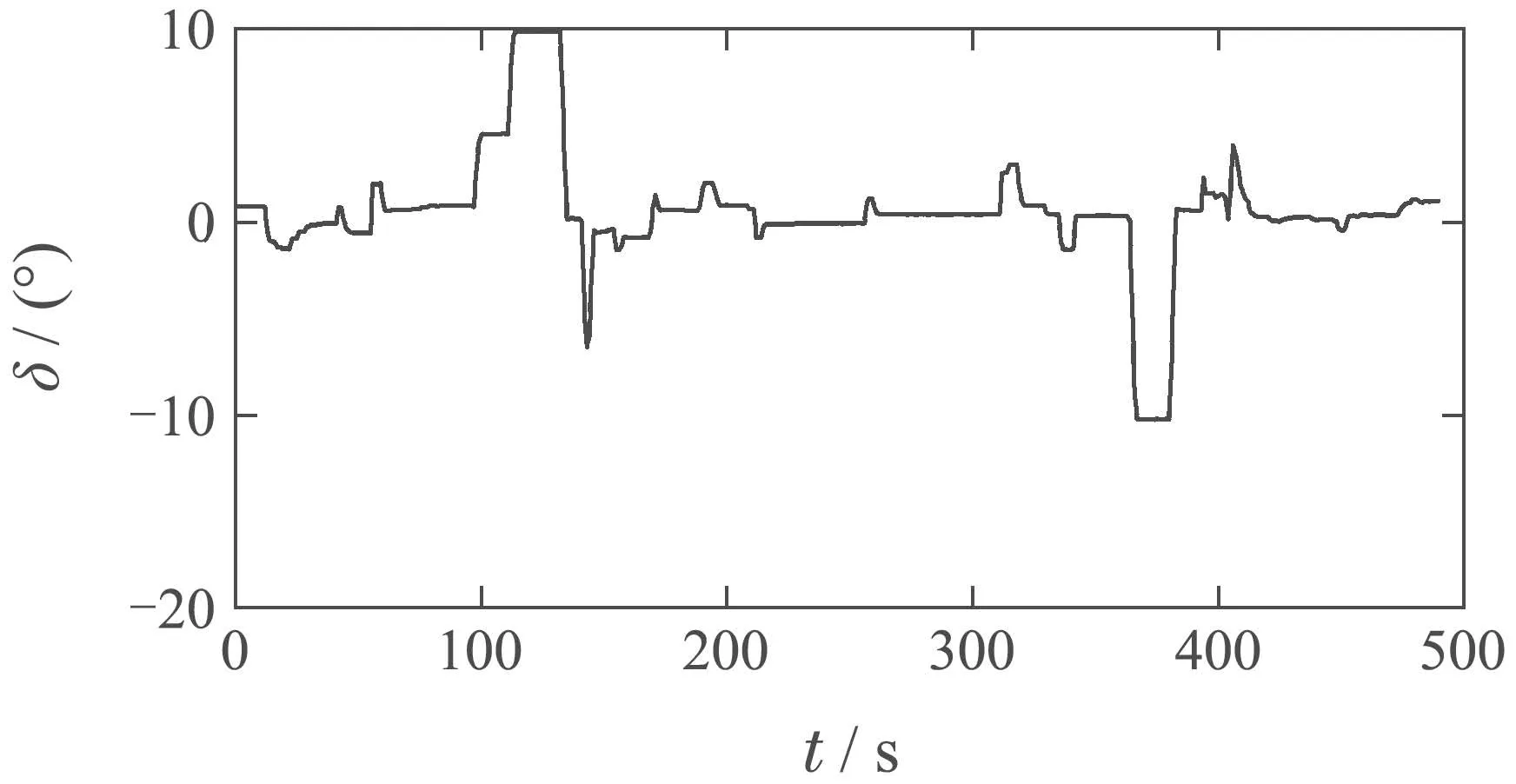
图8 测试数据3Fig.8 Test data 3

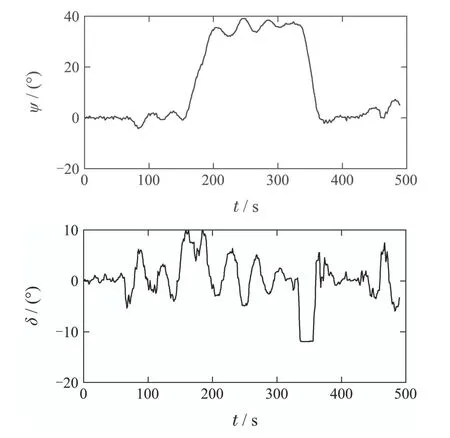
图9 测试数据4Fig.9 Test data 4

这5组测试数据基本涵盖了输出量的所有变化方式,包括航向大范围内随机连续变化(测试数据1,2)、航向突变(测试数据3,4)、航向保持(测试数据5).

用该5组测试数据依次测试各直接建模和间接建模方法下的4种模型,检测模型在各种复杂情况下的预测效果.表3-4展示了两种建模方法下一步预测输出均方根值和误差最大值.表3-4反映出通过间接建模得到的模型一步预测效果与直接建模基本相同,仅略好于直接建模.两者均方根值和最大误差相差基本在±0.1范围内,预测精度较高,但是偏差依旧存在.仅凭一步预测情况还不足以说明两者的区别,还需要分析长期预测结果.

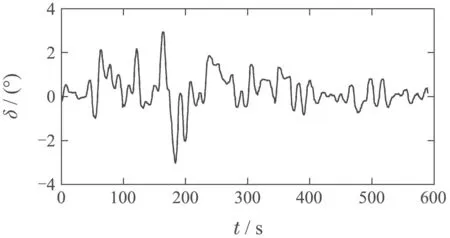
图10 测试数据5Fig.10 Test data 5

表3 一步预测直接建模/间接建模模型均方根值Table 3 RMS of the one-step prediction error for the direct modeling/indirect modeling models

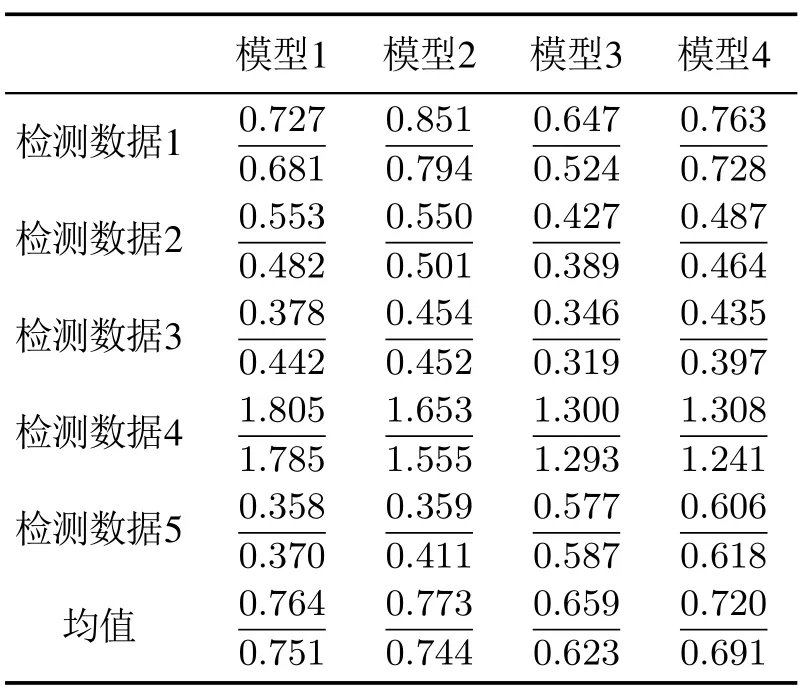
表4 一步预测直接建模/间接建模模型误差最大值Table 4 The maximum of the one-step prediction error for the direct modeling/indirect modeling models

图11-14展示了两种建模方法的4个模型分别在第2组检测数据下的长期预测结果以及预测误差.从后3个模型比较来看,在前150步,两种建模方法预测精度差距不大,但是两者与实际输出的误差依旧存在,并且随着时间的推移,这个误差越来越大.从150步后,两者的预测精度逐渐拉开差距,显然间接建模模型的预测效果要好得多.从发展趋势来看,间接模型的误差变化也平缓得多,到300步时,最大误差都在±40到±50之间.

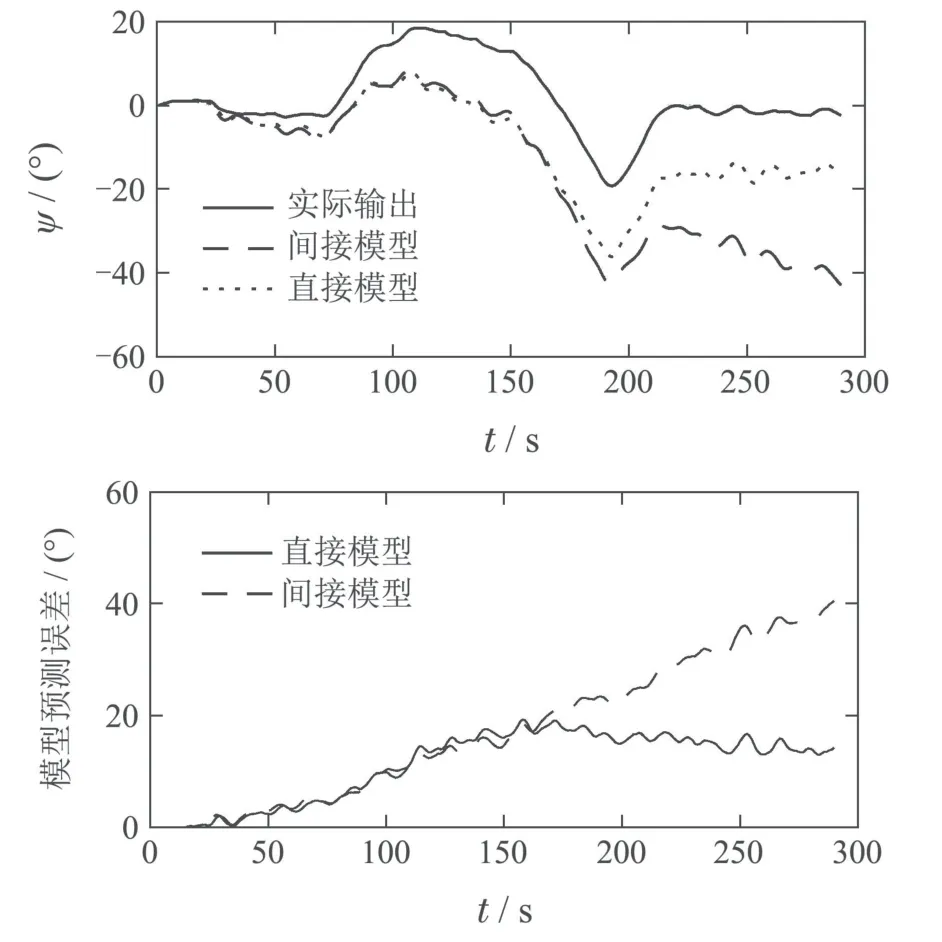
图11 模型1在检测数据2下的长期预测Fig.11 Long-term prediction of Model 1 under test data 2

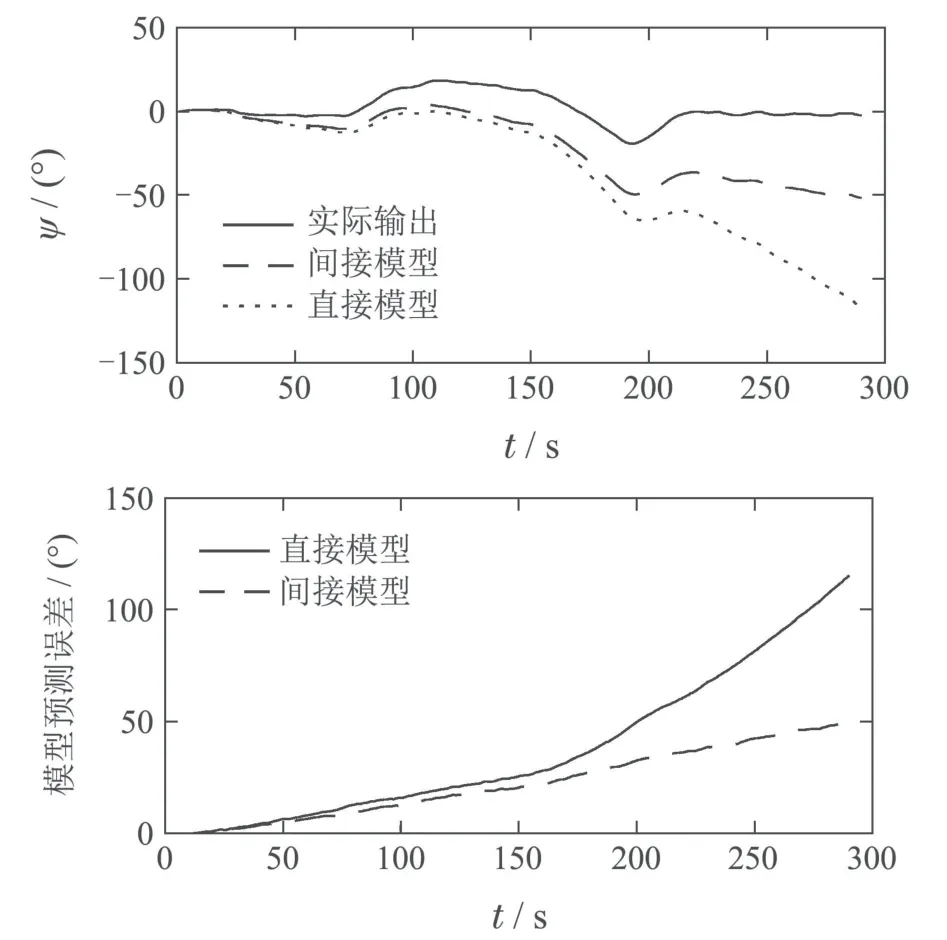
图12 模型2在检测数据2下的长期预测Fig.12 Long-term prediction of Model 2 under test data 2

但是第1个模型的直接建模要优于间接建模,通过表5-6的所有数据对比可以发现,直接建模对建模数据的依赖性比较大,而间接建模可以考虑到航向角偏差变化率,丰富了建模数据内容,因此4个模型在5组检测数据下的长期预测误差波动较小,在30～60区间内,对数据的依赖性较弱.相反,直接建模的长期预测误差在20～550区间内,波动幅度大,建模数据的好坏对基于数据驱动的船舶ARX模型有着重要的影响.

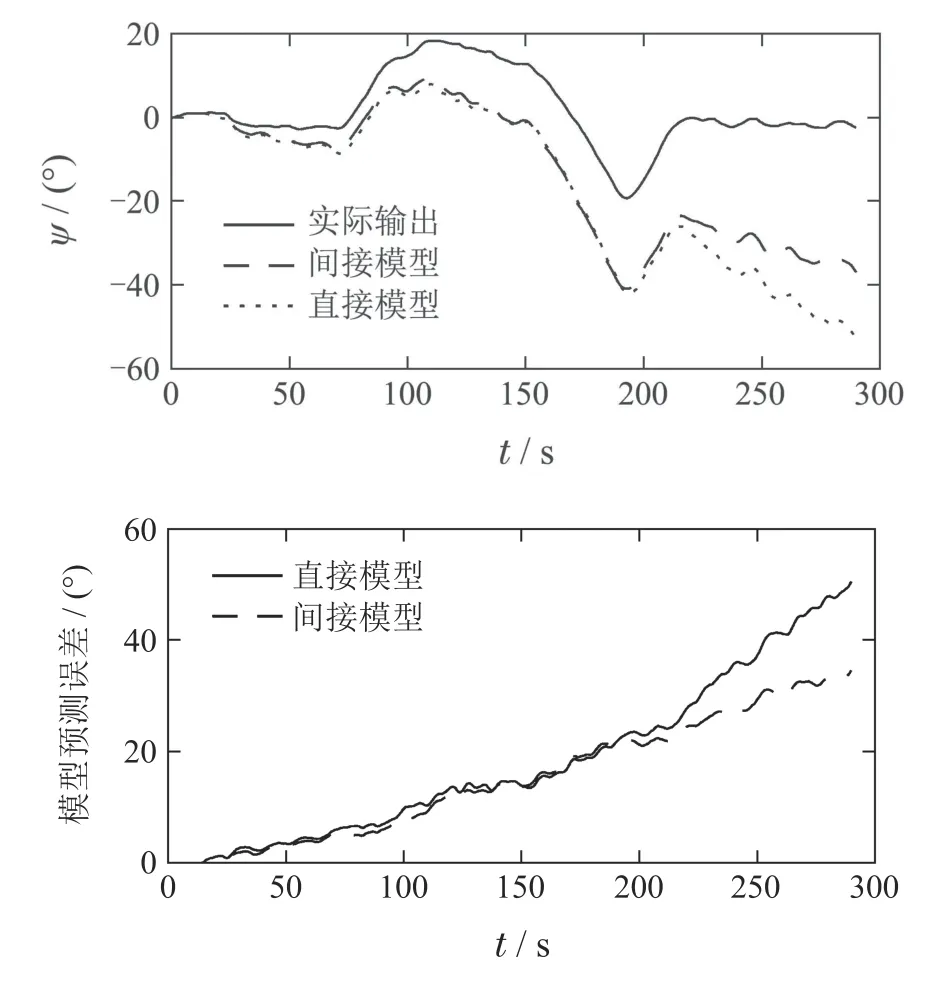
图13 模型3在检测数据2下的长期预测Fig.13 Long-term prediction of Model 3 under test data 2

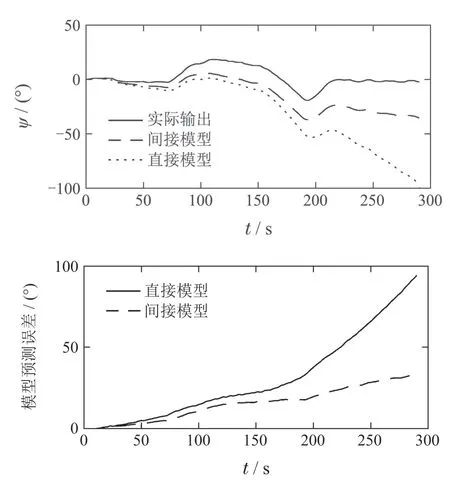
图14 模型4在检测数据2下的长期预测Fig.14 Long-term prediction of Model 4 under test data 2

综上所述,用于描述船舶航向控制的ARX模型需要大量的实际航行数据支持,但在实验场所有限和环境干扰的影响下,建模数据的测量可能是不完美的,并且数据的好坏还没有一个标准可以衡量,此时,间接建模便为该情况下提供了一个很好的方法.

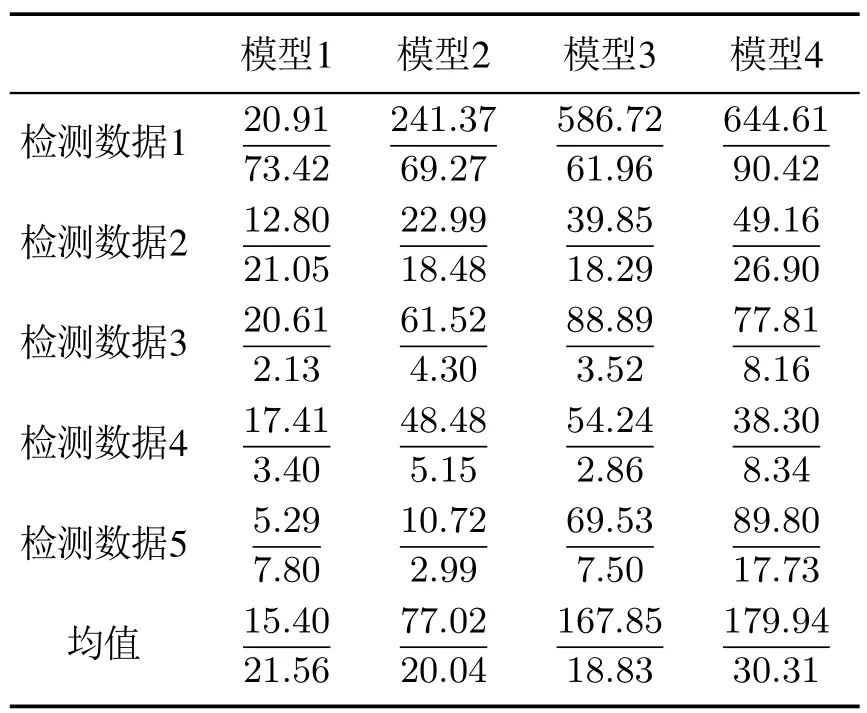
表5 长期预测直接建模/间接建模模型均方根值Table 5 RMS of the long-term prediction error for the direct modeling/indirect modeling models

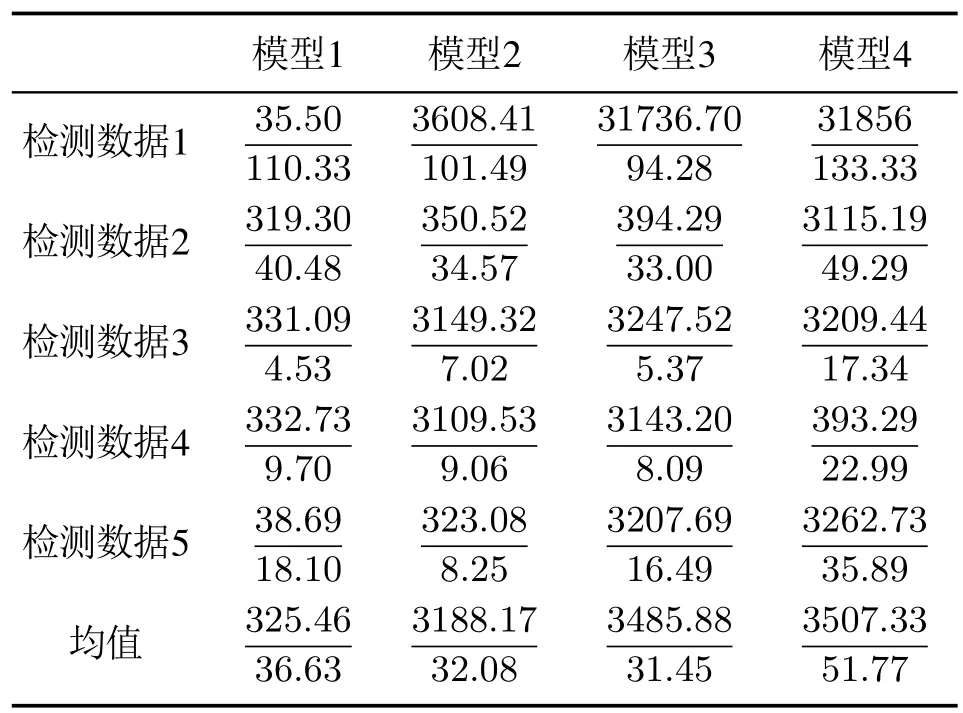
表6 长期预测直接建模/间接建模模型误差最大值Table 6 The maximum of the long-term prediction error for the direct modeling/indirect modeling models

4.3 最优模型选取

建模方法的改进是为了找到可以描述船舶动态性能更加准确的模型.对于间接建模模型,由一步预测数据可得,模型3、模型4的均方根值相对较小,其中均值最小的为模型3;在5组检测数据下模型3和模型4的最大误差在1.2～1.3之间,而模型1和模型2的均大于1.5.由长期预测数据来看,模型1、模型2和模型3优于模型4,并且模型3均方根值最小;长期预测最大误差只有模型4较大,均值在50以上,最优为模型3.

综上所述,间接模型3最优,同时说明一步预测效果好的不一定长期预测也好,选择模型的过程中要综合考虑一步预测和长期预测结果,没有绝对性的标准.

由图15可以看出,间接模型3有9个极点,并且有一个极点在单位圆上,说明模型处于临界稳定状态,符合船舶模型的稳定性特性.

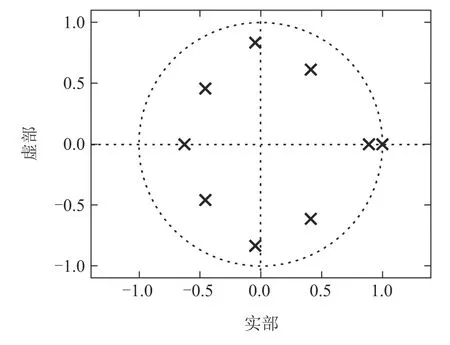
图15 间接模型3极点分布Fig.15 Pole distribution of the indirect Model 3

5 船舶对象的MMG模型

由于模型的选择很难有一个硬性的标准,探索更好的模型要不断比对更多不同的方法.通过物理建模得到的MMG模型同样可以描述船舶运动状态,并且已经沿用很多年.接下来将间接ARX辨识模型与之对比,找到一种可以在实验设备无法满足物理建模情况下的建模方法.

船舶运动的MMG模型建立要首先分析船舶流体动力及力矩的构成,分为作用于船体上的流体动力和力矩、螺旋桨上的流体动力和力矩以及作用于舵上的流体动力和力矩[15],其次要考虑船舶基本物理参数,例如船体质量、转动惯量和船速等,最后要设计实验,测试建模所需物理参数.

将船舶按照横向、纵向沿x轴,y轴进行解析,船舶数学模型写成[16-18]

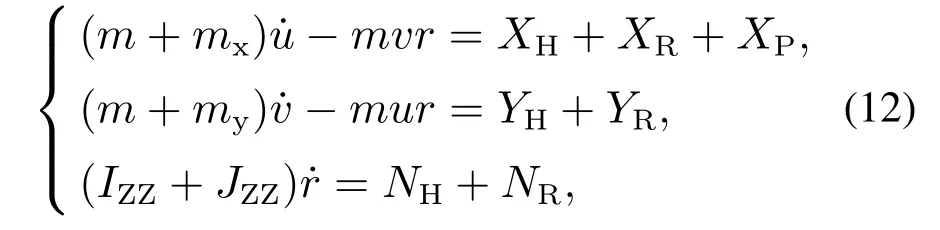
式中下标H,P,R分别表示船体、螺旋桨、方向舵.

作用于船体上的流体动力和力矩可表示为

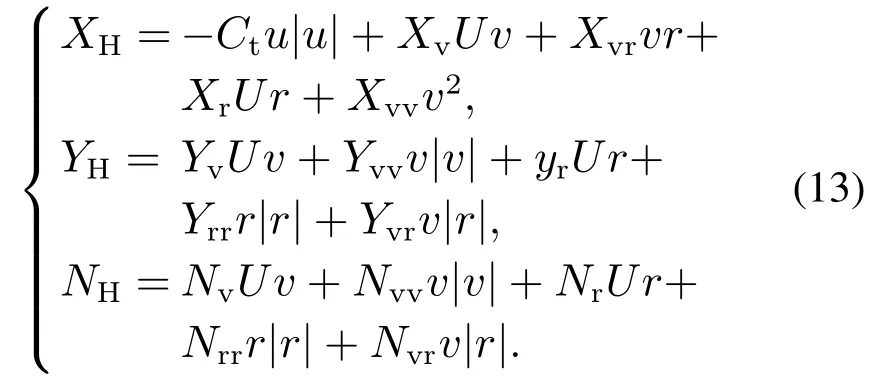
径向螺旋桨推动力与其纵倾角的关系为

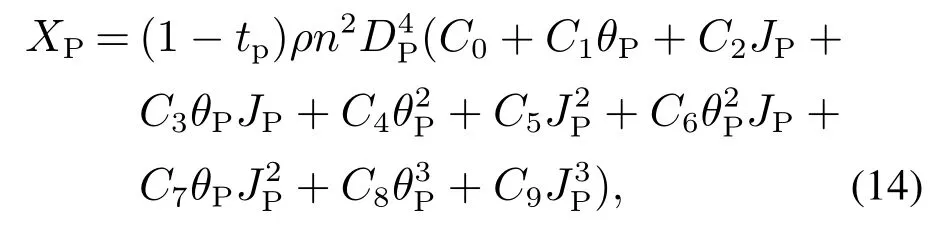
式中:XP为径向螺旋桨推力;C1-C9为推力系数;JP为推进系数;θP为螺旋桨纵倾角.

有效舵力与舵角的关系为

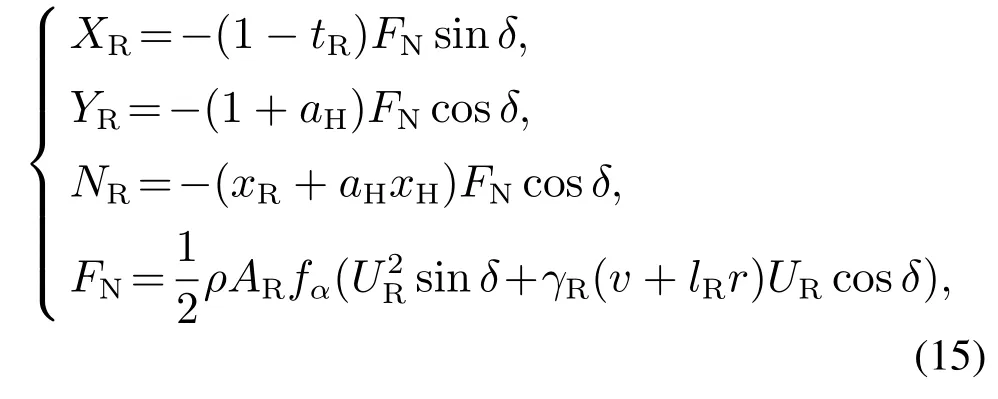
式中:δ为舵角;FN为舵法向力;XR,YR,NR为作用于船体的有效舵力;tR,αH,xH为船体与螺旋桨之间的水动力干扰系数;xR为舵位;AR为舵面积,fα为舵法向力系数;UR为舵的有效来流速度.

式(12)-(15)中其余物理参数如表7所示.

表7 物理参数Table 7 Physical parameter

利用特定实验测得“汐路丸”各种物理参数,得到其MMG模型,在同样5组检测数据下做MMG模型的长期预测,并将MMG长期预测结果与间接模型3的输出做出对比.

由图16-20可得在检测数据1下,MMG模型的长期预测效果稍优;在检测数据2和检测数据5下,间接ARX模型与MMG模型效果不相上下;在检测数据3和检测数据4下,间接ARX模型要优于MMG模型.由此说明,对于船舶这种复杂系统的建模,间接ARX模型和MMG模型长期预测效果相当,间接ARX模型可以作为一种替代方案应用于船舶航向预测的模型建模当中.

同时,MMG模型的建立要比辨识建模的方法复杂很多,必须要从船舶自身的机理出发,设计各种特定的水面实验,测定建模相关物理参数.例如要确定船舶附加质量和附加惯性矩现在还不能通过精确的计算而得,须通过设计振荡实验或冲击实验[15]而获得.

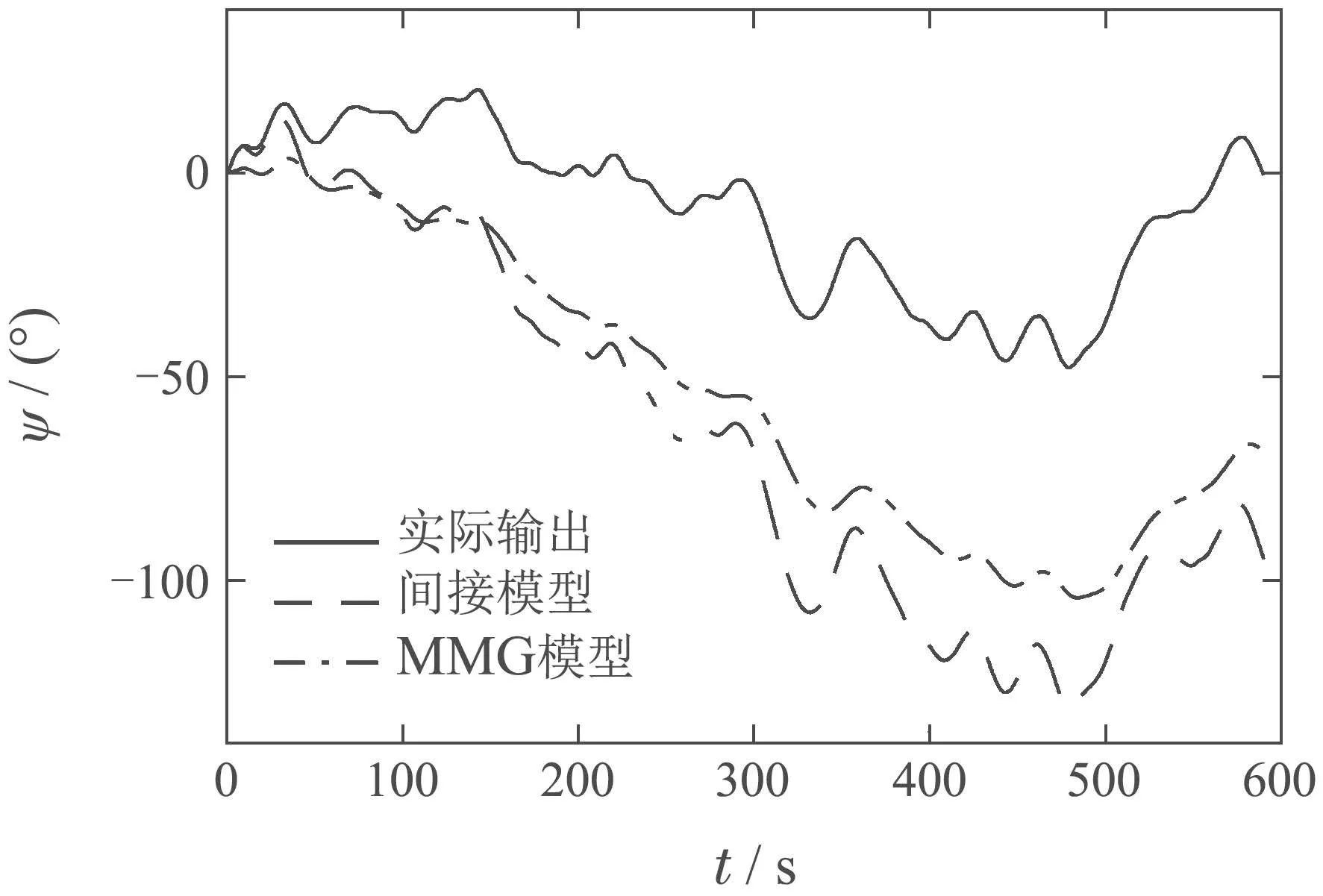
图16 在检测数据1下的间接ARX模型和MMG模型长期预测对比Fig.16 Long-term prediction comparisons between indirect ARX model and MMG model under test data 1

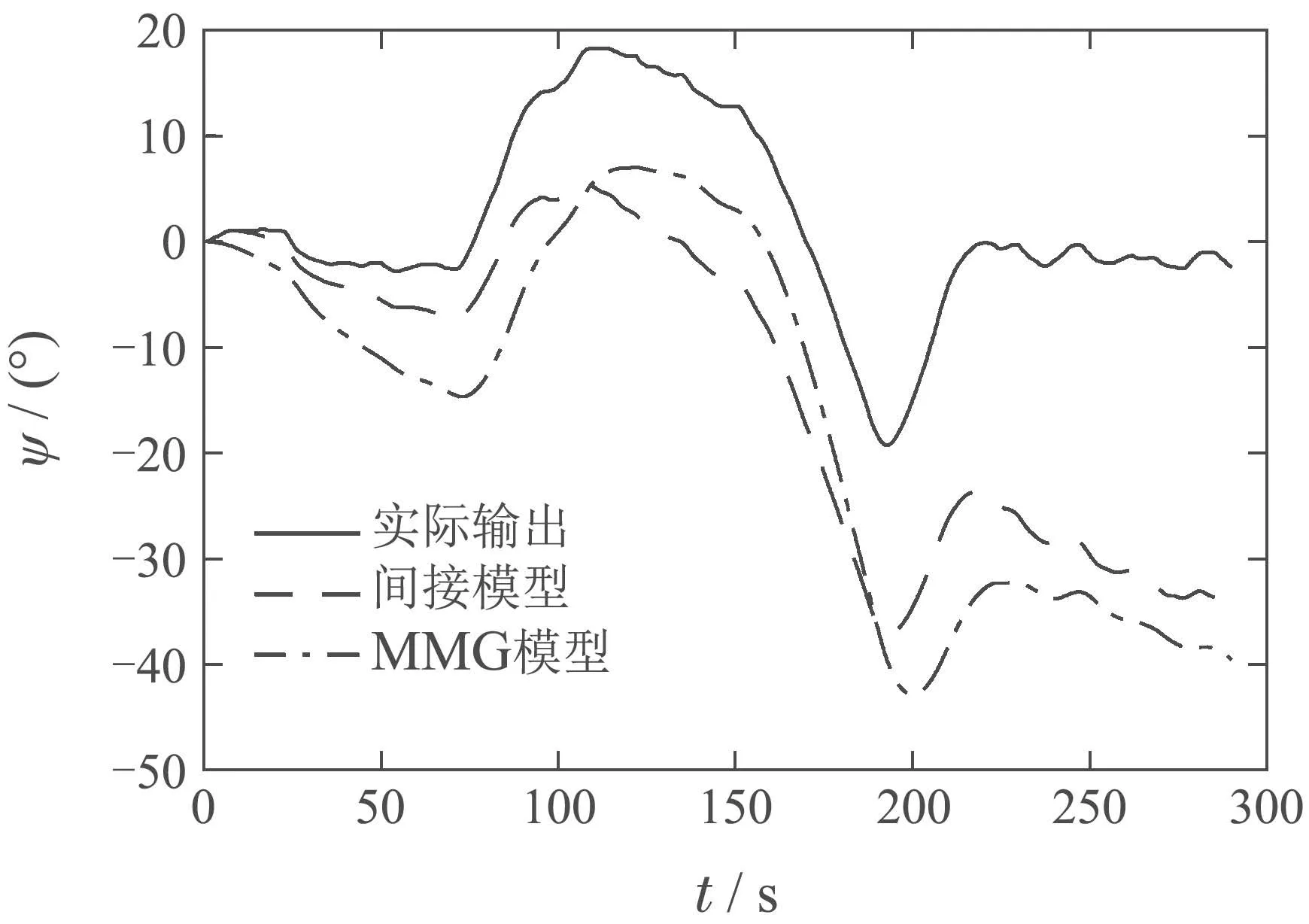
图17 在检测数据2下的间接ARX模型和MMG模型长期预测对比Fig.17 Long-term prediction comparisons between indirect ARX model and MMG model under test data 2

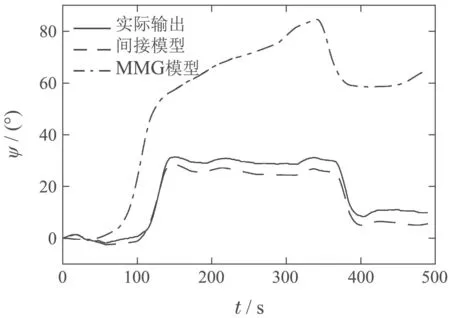
图18 在检测数据3下的间接ARX模型和MMG模型长期预测对比Fig.18 Long-term prediction comparisons between indirect ARX model and MMG model under test data 3

如表7所示,需要测定的物理参数至少有15个,在实验设备缺少、环境有限的情况下MMG建模有着极大的不便.而相较于MMG模型,间接ARX模型更为简单,并且对船舶艏摇角偏差的预测比直接ARX模型更好,这使得该建模策略具有一定的优越性和实际应用价值.

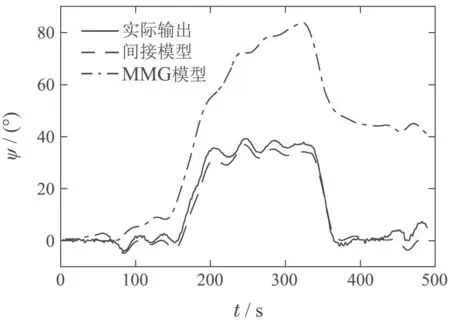
图19 在检测数据4下的间接ARX模型和MMG模型长期预测对比Fig.19 Long-term prediction comparisons between indirect ARX model and MMG model under test data 4

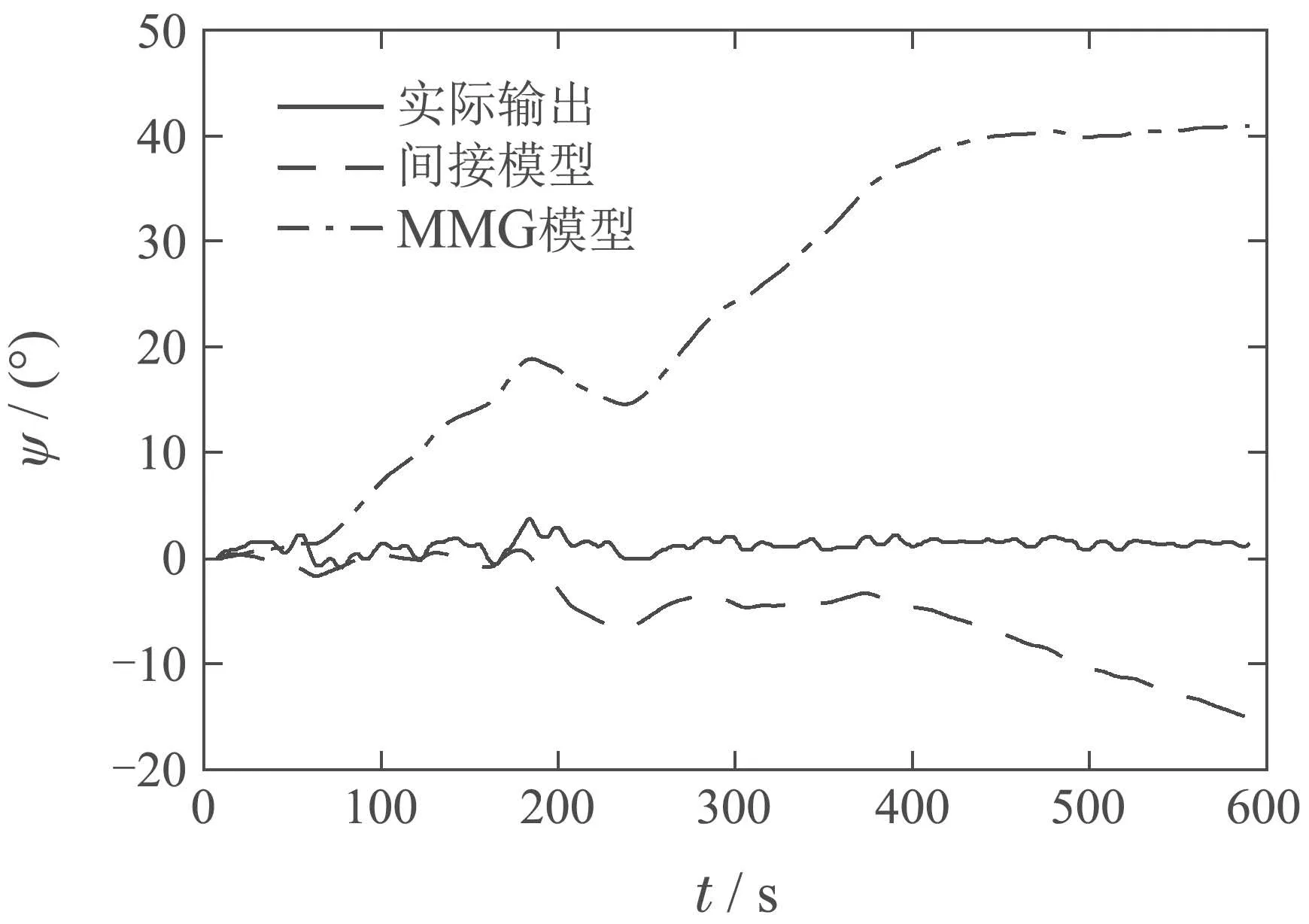
图20 在检测数据5下的间接ARX模型和MMG模型长期预测对比Fig.20 Long-term prediction comparisons between indirect ARX model and MMG model under test data 5

6 总结

针对东京海洋大学实验船舶“汐路丸”,利用系统辨识法建立了一个具有仿射结构的ARX模型来描述船舶的航向保持控制过程.综合考量AIC值、一步预测和长期预测精度等性能指标,得到相对最优的ARX模型,并于MMG模型进行了对比.

结果表明通过间接建模方式建立的ARX模型不止包含航向角偏差信息,还包含了航向角偏差变化率的动态特性,使得建立的模型对数据的解析更加完整,进而说明间接建模对建模数据的依赖性较低,在不同的建模数据下均能得到良好的建模效果.而直接建模的方法只有在建模数据好的情况下才能表现出令人满意的建模效果,否则长期预测结果将出现很大的误差.

同时,间接ARX建模方法相对容易,当建立MMG模型遇到困难时,便可以采用间接ARX建模法建模.