基于精英集的多目标差分进化聚类算法*
张明珠,曹 杰,王 斌
(南京财经大学信息工程学院,江苏 南京 210023)
1 引言
聚类技术是数据挖掘中的一种重要工具并被广泛应用在诸如信息检索、文本挖掘、图像处理和数据分析等领域[1 - 5]。作为一种无监督的学习问题,聚类将未被标记过的数据基于相似性或差异性划分成多个小组,使得同一小组内的对象尽可能相似,不同组间的对象尽可能相异[6]。一些聚类问题根据用户经验或领域知识可提前知道要划分成多少类,但实际情况中很难获取准确的聚类数。高估或低估聚类数都会损害聚类结果的质量,因此识别最佳聚类数是聚类分析中一个基本的问题。
对不知道聚类数的聚类问题,一种直接的思路是试错法(Trial-and-error)。首先获得每一种可能的聚类数的聚类结果,再按某种评价标准从众多结果中挑选一个最合适的聚类解[7],并且不同选择标准获得的最佳聚类数可能不同。为了获得多个不同聚类数的聚类结果,很多方法重复运行某个聚类算法,每次固定一个不同的聚类数[8]。这类方法简单易实施,但需多次运行,尤其当数据集较大或聚类数很多时,效率十分低下。如何更高效地获得不同聚类数的聚类结果同时保证每种聚类结果的质量,考虑到在同时优化具有多个相互矛盾或冲突的目标的问题时,不同于单目标优化问题只能获得一个最优解,基于种群的多目标进化算法可以得到一个包含多个近似最优解的解集。因此,本文尝试用多目标进化算法来同时得到多个不同聚类数的划分结果。
实际生活中很多问题需要同时优化具有多个相互矛盾或冲突的目标,不存在一个可行解使这些目标同时达到最优,这样的优化问题被称作多目标优化问题MOP(Multi-objective Optimization Problem)[9,10]。不失一般性,对于一个需要同时最小化m个目标的优化问题,其数学表达式为:
minx∈ΩF(x)=(f1(x),f2(x),…,fm(x))
(1)
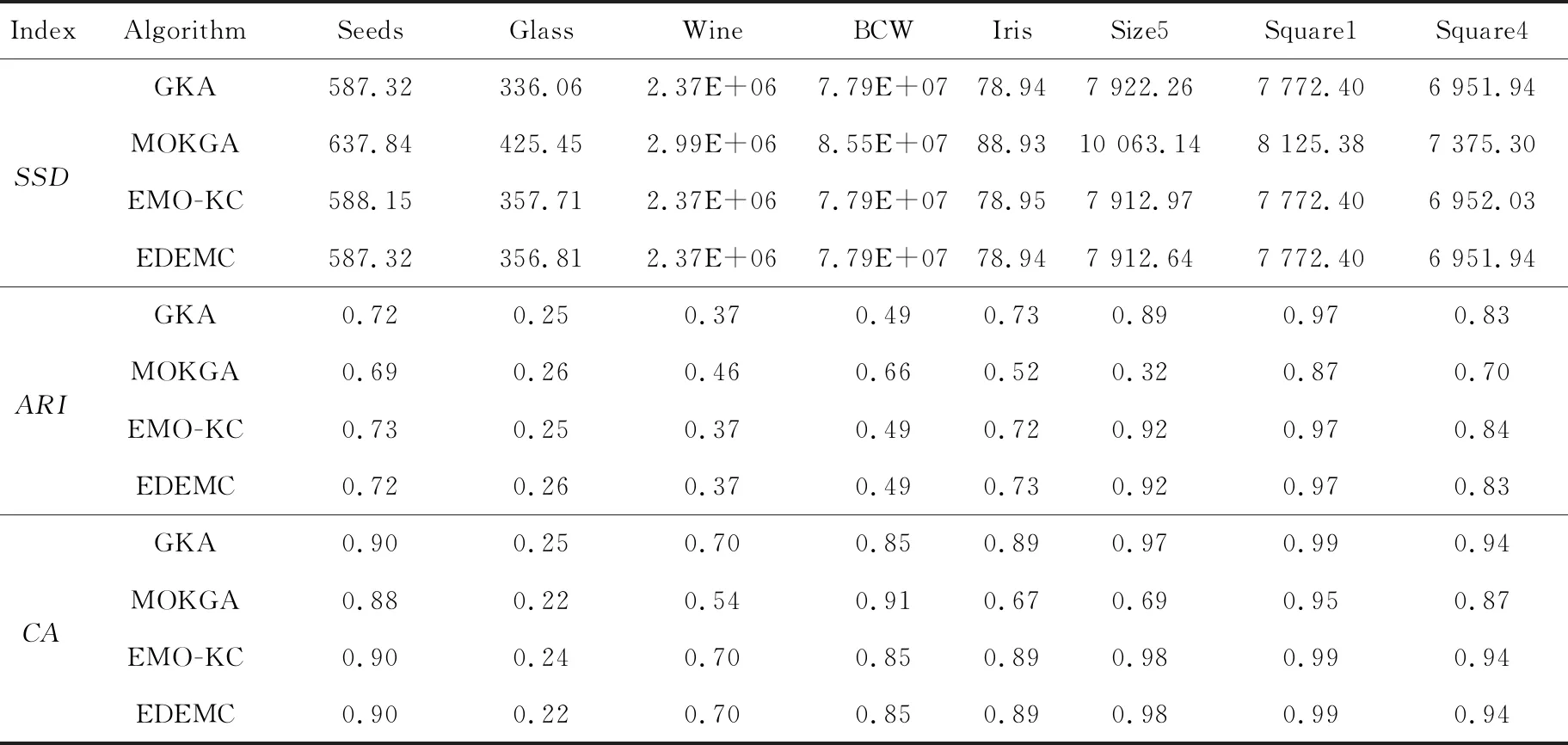
其中,x=(x1,x2,…,xb)∈Rb是一个b维的决策变量,Ω是包含所有可行解的解空间。目标函数F(x)定义了m个由决策空间向目标空间映射的函数。令x,y∈Ω,如果对所有的i∈{1,2,…,m},有fi(x)≤fi(y),且至少存在一个i使得fi(x) 聚类算法多通过最大化类内的紧致性和类间的分离性来获得高质量的聚类[12],然而聚类数与这2个目标有一定的冲突,即聚类数大的时候类间的分离性会变差,而聚类数小的时候类内的紧致性会减弱,选择合适的聚类数其实是在聚类数与类内紧致性和类间分离性的平衡中选择一个满意的折衷方案,从这一角度来说,从众多不同聚类数的聚类中选择一个聚类结果是一个多目标优化问题。聚类数作为一个能够反映数据结构的重要指标,本文直接将其作为一个优化目标,同时以优化聚类结果紧致性为例将各数据点到其聚类中心的平方距离的总和SSD(Sum of Squared Distance)作为另一个优化目标,将不知道聚类数的聚类问题转换为一个多目标优化问题来解决。以这2个指标为优化目标的多目标优化问题的PS中包含所有不同聚类数的聚类结果,且对优化类内紧致性来说,每种聚类数的聚类结果质量都达到全局最优。差分进化算法在很多文献中已经被证明具有良好的性能[13 - 15],因此,针对聚类数不确定的聚类问题,本文提出一个多目标差分进化EDEMC(Elitist-archive-based Differential Evolutionary algorithm to Multi-objective Clustering)算法同时优化2个聚类指标,以得到不同聚类数的聚类结果。 本文的主要贡献在于: (1)定义了一个新的精英集来保存每一种聚类数的历史最优聚类结果并使之参与种群的差分进化; (2)设计了新的重组算子,对子代进行局部搜索和修复; (3)提出了一种补充策略提高种群的多样性。 对于一个多目标进化聚类算法,一条染色体往往代表了一个完整的聚类解。多目标进化聚类算法的一般流程是[16]:(1)选择一个合适的编码方式表示聚类结果,初始化种群;(2)选择多个聚类有效性指标作为优化目标;(3)设计合适的进化操作方式,包括选择、交叉和变异;(4)使用有效的环境选择方式维持种群的收敛性和多样性;(5)从Pareto最优解集中挑选一条最优染色体解码为聚类的结果。 不同于聚类数已知的聚类问题,Handl等人[17]提出了一种自动确定聚类数并得到该聚类数的聚类结果的多目标进化聚类算法。该算法用一种Locus-based Adjacency Graph的编码方式表示聚类结果,染色体长度等于数据点的个数n,每一个基因位上的值是[1,n]中的一个整数,如果基因位i上的值是j,则表示数据点i和数据点j有联系,这2个数据点归为同一类。Wikaisuksakul[18]在初始化种群时,对每条染色体从给定的聚类数的范围中随机选择一个作为其有效的聚类数并依此对聚类中心编码,即若数据点维度是d,染色体的聚类数是K*,那么该条染色体的长度为d*K*。Özyer等人[19]在初始化时对每一条染色体在给定聚类数的范围中随机选取一个整数K*作该染色体的聚类数,因为采用基于标签的染色体编码方式,所以染色体上每个基因位的值代表类标签,基因位的取值为[1,K*]中的随机整数,代表了该基因位对应数据点所属的类。上述3种方式求得的Pareto解集都包含了多个不同聚类数的聚类解,但可能不包含范围内所有聚类数的解,甚至缺少真实聚类数的聚类解,导致从种群中选择最佳聚类数的聚类结果时产生偏差。于是,Wang等人[20]将聚类数K设为优化目标,将各个数据点到其聚类中心的平方距离的和设为另一个优化目标,但对平方距离和的目标函数进行了转换,保证2个优化目标之间绝对冲突,使代表不同聚类数的染色体的目标向量之间互不支配,这样在基于非支配排序和拥挤度的环境选择中各K值均至少有一条染色体被选中并遗传到下一代,使得Pareto解集中每一个K都有染色体存在。但是,因未考虑对无效簇的处理,即某些聚类中心没有任何数据点附属,染色体代表的聚类数是不真实的,因此实际的解集中可能有些聚类结果是缺失的。本文所提算法在进化过程中不仅对不合法的染色体进行修复,使每一条染色体被赋予的聚类数都是真实、有效的,还在种群缺少任意一个聚类数K对应的染色体时,生成新的优良染色体补充到种群中,提高种群的多样性。 进化算法中精英集的提出主要是为了提高算法的收敛速度[21],如文献[22]提出用保存了优良染色体的外部种群(External Population)参与每一代进化,将父辈与外部集组合到一起后通过比较支配强度赋予染色体适应度,挑选支配性更强的染色体参与繁殖。精英集也被用于保持种群的多样性。文献[23]创建了2个档案(Archive)分别用于维持种群的收敛性和多样性,并且2个档案采用不同的进化操作以更好地实现各自的功能。本文算法中的精英集针对本文待解决问题的特点,保存每一个聚类数K对应的历史最优聚类解,利用精英集补充种群中缺失的K值的染色体,增加种群的多样性;另外,精英集参与差分进化生成新染色体,使更多有利基因片段遗传到下一代,促进种群快速收敛。 本文提出的基于精英集的多目标差分进化聚类算法EDEMC的主要流程如算法1所示。 算法1基于精英集的多目标差分进化聚类算法EDEMC 输入:数据集Data,最小聚类数Kmin,最大聚类数Kmax,种群规模N,最大迭代次数maxGen,交叉概率CR,缩放因子F。 输出:精英集E。/*E中含有每一种聚类数的近似最优聚类结果*/ 步骤1初始化种群P和精英集E,每一条染色体代表一个聚类数K的聚类解; 步骤2主循环: (1)用二进制锦标赛的方式从P中选择N条染色体组成交配池MatingPool; (2)利用DEbest遗传操作生成子代Q。具体地,对MatingPool中每一条染色体si,i=1,2,…,N: ①用式(5)的方式生成变异染色体vi; ②对vi按式(6)生成交叉染色体ui; ③利用one-step-K-means对ui进行局部搜索,并修复ui的有效聚类数,生成染色体qi。 (3)依据非支配排序和拥挤度对集合{P,Q}进行环境选择,生成过渡种群P′; (4)Supplement(P′,E,Data),检查P′是否含有给定范围内每一个聚类数的聚类解,若存在缺失,利用精英集对之进行补充; (5)精英集E和种群P′互相更新每一个K的最优聚类结果,将更新后的P′赋值给P作为下一代的父辈; (6)是否满足停止条件,若未满足,返回(1)。 算法2Supplement// 检查并补充染色体 输入:过渡种群P′,精英集E,数据集Data。 输出:过渡种群P′。 步骤1检查过渡种群P′中是否含有所有聚类数K对应的聚类结果,缺失的聚类数的值组成集合lostK; 步骤2补充种群P′中缺失的K的染色体,对每一个K∈lostK: (1)找到精英集E中K-1对应的聚类解,解码,拆分其中最为分散的一个簇,生成新的染色体,记为s1; (2)找到精英集E中K+1对应的聚类解,解码,合并最相近的2个类簇中更分散的一个簇,生成新的染色体,记为s2; (3)比较精英集E中K对应的聚类解与染色体s1、s2的支配性,将更优的染色体添加到P′中,若三者互不支配则随机选择。 算法的目标是获得所给范围[Kmin,Kmax]内所有聚类数K对应的聚类结果,Kmax和Kmin是用户给定的聚类数K的上下界,从而生成2个优化目标——最小化聚类数K和类内平方距离和SSD——的Pareto最优解集,2个目标函数的计算方式如式(2)和式(3)所示: (2) f2=K* (3) 其中,K*是当前染色体代表的聚类解的有效聚类数。ck是类Ck的中心,类中心的计算方式见式(4),|Ck|是类Ck包含的数据点的总数。pi∈Rd是一个属于类Ck的d维数据点。distance(x,y)是一个计算数据点x与数据点y之间距离的函数,本文采用欧氏距离。聚类过程中将每个数据点划归到与之距离最近的一个簇中,数据点与类的距离按数据点到类中心的距离计算。 (4) 进化算法一般将种群表示为一个矩阵,一个N*n的矩阵表示种群含有N条染色体,每条染色体长度为n。本文采用实数编码的方式将聚类中心编码进染色体,具体编码方式可参考图1。其中,染色体长度统一为n=d*Kmax,d为数据点的维度,Kmax是最大聚类数,K*是染色体代表的聚类解的有效聚类数,ci,j表示聚类中心ci的位置坐标的第j个元素。染色体中前d个基因位上的值是第1个聚类中心的位置坐标,接下来的d个基因位上的值是第2个聚类中心的位置坐标,以此类推。每一条染色体被随机赋予一个[Kmin,Kmax]中的整数K*作为真实的聚类数,即只有前d*K*个基因位上的值是该染色体对聚类中心真实有效的编码。 算法首先随机初始化一个包含多条染色体的种群,代表了对问题的多种解。随机初始化能够增加种群的多样性,提高种群的搜索能力。本文初始化种群时需要使每一个聚类数K至少有一个解存在,另外为了使染色体合法,即每一个类至少有一个数据点附属,对每一条染色体,从数据集中随机选择Kmax个不同的数据点作为聚类中心,然后结合染色体实际的K*值,计算染色体的目标向量。 Figure 1 Encoding scheme of chromosome图1 染色体编码示意图 精英集的大小为(Kmax-Kmin+1),用于保存目前为止所得染色体中每一种聚类数K对应的最优染色体。初始化时找到种群P中不同K对应的所有染色体,并从中挑选SSD值最小的染色体作为该K值的最优解保存到E中。 利用二进制锦标赛的方式从P中挑选N条染色体组成交配池MatingPool。详细操作可参考NSGA-II(Nondominated Sorting Genetic Algorithm-II)[24]。对MatingPool中的每一条染色体用类似DE/current to best/1[25]的方式生成后代,该操作记作DEbest。首先按式(5)生成变异染色体vi,si是待操作的父体,sbest是与si具有相同真实聚类数K*的历史最优染色体,即E中K*对应的染色体。sr1和sr2是从P中随机选择的2个不相同的染色体。参数缩放因子F∈(0,2]。 vi=si+F*(sbest-si)+F*(sr1-sr2) (5) 变异后,用式(6)生成交叉后的染色体ui=(ui,1,ui,2,…,ui,n),n=Kmax*d。 j=1,2,…,n (6) 其中,CR是交叉概率;rand是一个[0,1]的随机数;jrand是一个[1,n]的随机整数,用于保证ui和si至少有一个基因位不同。 新生成染色体的聚类数K值从其父代遗传。生成ui后,根据其K值,即si的K*值,解码ui得到聚类中心,依据划分结果用one-step-K-means[19]局部搜索,更新一次聚类中心(如式(4)所示),删去无效中心后得到新染色体qi并计算优化目标值。对MatingPool中每一条染色体进行上述操作后生成Q={q1,q2,…,qN}。对[P,Q]用文献[24]中的方式进行环境选择选出N条优良染色体组成过渡种群P′。 为保证每一个聚类数K在种群中都存在聚类解,有机会参与进化和交换信息,首先检查在过渡种群P′中是否每一个K值都有对应的解存在,若存在缺失,则利用精英集中的染色体生成新染色体补充到P′中,生成新种群P。生成新染色体时主要采用的思想是合并与拆分,有很多文献[7,26]展示了该方式对提高聚类结果质量的促进作用。补充K后生成的种群P大小不固定,但不小于N。 首先,根据过渡种群P′中所有染色体对应的聚类解的聚类数,找出缺少的聚类数K。对每一个缺失的K值,从精英集E中找到其前后K值对应的聚类解的染色体,即代表了聚类数为K-1和K+1的聚类解的染色体,分别记为e(K-1)和e(K+1)。将e(K-1)中最分散的类拆分成2个,增加1个类;将e(K+1)中距离最近的2个类中更分散的类中的数据点合并到其它簇中,减少1个类。比较产生的新的聚类结果(染色体)是否优于(支配)精英集E中K对应的染色体e(K),若是,则将e(K)替换成更优的染色体。最后将e(K)添加到P′中。 每个类的分散程度用该类中所有数据点到聚类中心的平方距离和的均值衡量,即: (7) 类之间的距离用聚类中心间的欧氏距离度量,即类Ci和类Cj的距离为: distance(Ci,Cj)=distance(ci,cj)= (8) 拆分过程中将最分散的类拆开。挑选该类中离簇中心最远的数据点和离簇中心最近的数据点作为新的聚类中心,删去该簇的初始中心,将该簇中剩余的数据点依据新生成的2个中心重新划分。划分结果用one-step-K-means方法更新一次聚类中心后,将新的聚类中心编码到染色体中,依此生成新染色体替换原来的染色体。合并过程中首先找到距离最近的2个类,将更分散的类中的数据点根据数据点到其它聚类中心的远近分配至距离最近的簇中,随后同样用one-step-K-means方法更新一次聚类中心,将新聚类中心编码生成染色体替换原染色体。需要注意的是,拆分与合并的方式不止这一种,本文采用此种方法一方面是因为在多次迭代过程中具体的操作方式对种群整体的表现影响不大,另一方面是可以减少对距离的计算。 对于本文提出的EDEMC算法,其时间复杂度分析如下:在每一次迭代中,时间复杂度由2个部分组成:第1部分是环境选择中的非支配排序和拥挤度计算,其时间复杂度为O(mN2);第2部分是计算染色体的优化目标和划分聚类,该过程中需要计算距离,时间复杂度为O(NNdataKmaxd)。其中m为优化的目标数,N为种群的染色体数,Ndata为数据集中数据点的个数,Kmax为最大聚类数,d是数据点的维度。因此,当算法迭代次数为maxGen时,算法总的时间复杂度为O(maxGen*(mN2+NNdataKmaxd))。 本节对本文算法进行验证和分析。实验主要分为3个部分,第1部分用于分析算法总体的表现,以及验证算法中一些关键操作对算法性能的提升作用。为了评估本文算法聚类结果的收敛性,即聚类结果的类内紧致性,第2部分将本文算法与GKA(Genetic K-means Algorithm)[27]进行比较。第3部分主要为了验证算法是否能够有效获得多种不同聚类数的聚类结果,将所提算法与MOKGA(Multi-objective K-means Genetic Algorithm)[19]和EMO-KC(Evolutionary Multi-objective Optimization K Clustering)[20]算法进行对比,这里将MOKGA中同样反映聚类结果紧致性的优化目标TWCV(Total Within-Cluster Variance)改为SSD,以便于比较。 本文采用调整的兰特指数ARI(Adjusted Rand Index)和聚类准确性CA(Clustering Accuracy)[12]作为评价指标。ARI通过统计正确决策的样本对数来评价算法性能,CA比较预测结果与真实结果的一致性来评价聚类准确度。2个指标取值均在[0,1],值越大表示聚类效果越好。 实验数据集包括3个模拟生成的二维数据集(https://personalpages.manchester.ac.uk/staff/Julia.Handl/generators.htm)和UCI(http://archive.ics.uci.edu/ml/index.php)中的5个真实数据集。模拟数据集均包含1 000个维度为2的数据点,且数据集中数据点可划分为4个类簇。真实数据集的大小各不相同,最大的数据集Breast Cancer Wisconsin包含569个数据点,数据点的维度高达30。各数据集的具体信息如表1所示。在各进化聚类算法的最大迭代次数的参数设置中,对模拟数据集设置的值均为500,对真实数据集中数据维度为13及以下的数据集设置的值为1 000,而对数据集Breast Cancer Wisconsin设置的值为2 000。聚类数的取值设为[2,20],种群大小N=100,EDEMC中交叉概率CR=0.9,缩放因子F=0.3。算法GKA、EMO-KC和MOKGA中的其它参数使用各自原文中推荐的值。各数据集的具体信息如表1所示。实验在CPU为3.6 GHz,RAM为16 GB的Windows 10操作系统上进行。 Table 1 Features of experimental datasets表1 实验数据集的特性 为了简要展示算法的聚类效果,从每一个数据集的一系列聚类解中选择已知的正确聚类数对应的解为例进行说明。表2是各算法在所有数据集的真实聚类数上所得聚类结果的SSD、ARI和CA。 从表2中可以看到,在全部8个数据集上,EDEMC算法在7个数据集上得到的聚类结果的SSD不大于其它算法的,4个数据集上的ARI不小于其它算法的,6个数据集上的CA不小于其它算法的。综合来看,EDEMC在大部分数据集上都能够获得良好的聚类结果。 在维持其它操作不变的情况下,将EDEMC中补充聚类数的聚类解的过程替换为直接从精英集中将聚类数K对应的个体加入到当前种群的方式,记该算法为EDEMC1;将EDEMC中DEbest操作修改为模拟二进制交叉和多项式变异,交叉概率为0.9,变异概率为1/n,n为染色体的长度,分布指数均为20,记该算法为EDEMC2。各算法的其它参数按照前文进行设置。在数据集Square4上运行EDEMC1、EDEMC2和EDEMC各10次,对所得结果取平均值,结果如图2所示,EDEMC的Pareto前沿在EDEMC1和EDEMC2的Pareto前沿的下方,即在相同聚类数的情况下,EDEMC聚类结果的SSD小于EDEMC1和EDEMC2聚类结果的,这表明了填补策略中拆分-合并操作和DEbest操作的有效性。 Table 2 SSD,ARI and CA of clustering results of each compared algorithm on datasets under their true number of clusters表2 真实聚类数下各算法在数据集上的聚类结果的SSD,ARI和CA Figure 2 PF of EDEMC,EDEMC1 and EDEMC2 on dataset Square4图2 EDEMC、EDEMC1和EDEMC2 在数据集Square4上所得的PF 因为GKA算法假设聚类数已知,需要将之作为算法的输入参数,对每一个K∈[Kmin,Kmax],GKA均需运行一次。为公平比较运行时间,对每一个K值,GKA的最大迭代次数为小于maxGen/(Kmax-Kmin+1)的最大整数,如此GKA获得所有K值的聚类结果所用的迭代次数将不大于EDEMC运行一次所用的最大迭代次数。这里选取数据集Iris进行实验。图3是EDEMC与GKA算法的实验结果,包括实验所得的K与SSD的结果以及对应K的ARI值。可以观察到,EDEMC运行一次与GKA运行多次后的结果均涵盖了每一个K值的划分,并且对每一个K,两者的类内平方距离和近似,ARI互有优劣,这表明本文算法在同时优化2个目标的情况下得到的聚类效果不比全力优化其中一个目标得到的聚类效果差。表3所示是各算法总的运行时间,从中可以看到,在相同或更少的总迭代次数下,GKA的运行时间远远大于EDEMC的,主要是因为GKA需要多次运行才能得到各种聚类数的聚类结果,并且GKA中每次变异都需要计算各变异点到聚类中心的距离,增加了计算时间,尤其当数据点较多或数据维度较高时,距离计算非常耗时,如数据集大小为(150,4)的Iris,GKA的用时约为EDEMC的5倍,而在大小为(1 000,2)的数据集Square1上,GKA的用时增长为EDEMC的15倍左右。 Figure 3 Experimental results of EDEMC and GKA on dataset Iris图3 EDEMC和GKA在数据集Iris上的实验结果 Table 3 Running time of each algorithm 以真实数据集Iris、Glass和模拟数据集Square4上的实验为例,图4是EDEMC、MOKGA和EMO-KC算法的实验结果。只考虑算法最终所得解集中分别保留了多少个不同聚类数的解时(这在本文中反映了种群的多样性),从图4中可以观察到,MOKGA算法所得聚类解集对应的PF多处有断裂,意味着缺少很多聚类数K对应的聚类解;EMO-KC算法对应的PF分散性较好,在大部分数据集上只在线段尾端发生残缺,说明EMO-KC在这些数据集上缺少较大聚类数的聚类解。本文所提EDEMC算法所得聚类解集的PF对应的线段连贯、完整,说明其多样性最好。 整体而言,EMO-KC算法的多样性优于MOKGA算法,但EMO-KC和MOKGA都可能存在缺失的聚类数,分析原因如下。虽然EMO-KC算法中设计的优化目标函数使得不同聚类数的染色体间互不支配,环境选择过程中这些非支配解也会被保留,但因为遗传操作的随机性,会有聚类中心没有任何染色体附属,即存在空簇,去掉无效的聚类中心后染色体实际的聚类数目会少于K,便可能导致最终输出中没有该聚类数对应的聚类结果。本文算法会检查是否存在无效的聚类中心,并且删去空簇后会修正染色体的实际聚类中心和聚类数K,如果种群丢失了某些K的聚类解,则利用精英集补充种群中缺失K的聚类解,因此不同大小的K都有染色体参与进化,精英集中染色体的聚类数目都是真实有效的。MOKGA算法采用标签编码,不存在无效簇,但变异使得染色体的聚类数K动态变化,并倾向于越来越小,尤其当数据集的真实聚类数较大时,初始阶段的进化过程中可能会将具有真实聚类数的染色体淘汰掉。MOKGA输出的PS中可能具有多个不同K的聚类解,但不能保证每一个K值都有染色体存活到最后,也就是说同样会存在丢失聚类数的聚类结果的情况。 EDEMC算法不仅能够一次性给出给定范围内所有聚类数K的聚类结果,且聚类结果的质量较高。实验显示,EDEMC的类内平方距离和SSD均小于或等于EMO-KC和MOKGA算法聚类结果的。在图4中表现为,EMO-KC的PF对应的线段位于EDEMC的PF对应的线段的上方,而MOKGA解集的PF对应的线段远在两者的上方。总体而言,在解集的分布性和收敛性2方面本文所提EDEMC算法均为最优。 运行效率方面,因为MOKGA算法中采用基于距离的变异和one-step-K-means操作,因距离计算耗时的原因导致MOKGA在3者中用时最长;EDEMC算法中同样用到了one-step-K-means,并且当种群中不存在某个聚类数K的聚类解时,为生成该K的聚类解需要对类簇进行拆分和合并,也需多次计算距离,因此EDEMC的运行时间略长于EMO-KC算法的。 Figure 4 Experimental results of EDEMC,EMO-KC and MOKGA on real-world datasets Iris, Glass, and synthetic dataset Square4图4 EDEMC、EMO-KC和MOKGA在真实数据集 Iris、Glass和模拟数据集Square4上的实验结果 不同于现有的通过重复运行从而获得多个不同聚类数的聚类结果的算法,本文将聚类作为一个多目标优化问题同时最小化聚类数K和类内平方距离和SSD,通过新的多目标差分进化算法一次性获得多种聚类数的聚类解。算法创建并维持一个保存了各个聚类数的历史最优结果的精英集,通过新的遗传操作和补充策略让种群迭代优化,最后输出各个聚类数K的近似最优聚类结果组成的Pareto解集,获得多个不同的聚类数与类内平方距离和的平衡。实验表明了所提算法的有效性,以及补充策略和差分进化对算法性能的提升。与GKA、MOKGA和EMO-KC算法在多个模拟数据集和真实数据集上的对比实验表明,本文所提算法不仅能在较少的时间内获得分布更广的Pareto解集,并且所得的解具有良好的收敛性——这里表现为具有更小的SSD。 本文算法给出了多个K值的聚类结果的可选项,未来将研究如何充分利用Pareto解集的信息从中得到最终的聚类。另外,本文算法的优化目标是用尽可能少的聚类数使类内平方距离和最小,可以考虑引入更多能够反映不同数据结构特性的优化目标,当优化3个以上的目标时可用类似文献[28]中的算法对超多目标的优化问题进行优化。最后,当处理大样本或高维数据时,面对快速增长的搜索空间,可尝试用大规模多目标优化算法[29]实现多目标聚类。2 相关工作
3 基于精英集的多目标差分进化聚类算法
3.1 初始化

3.2 重组和择优
3.3 检查并补充K
3.4 更新精英集
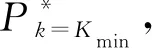
3.5 时间复杂度
4 实验结果与分析
4.1 实验设置

4.2 EDEMC的总体表现

4.3 EDEMC与GKA的对比


4.4 EDEMC与MOKGA、EMO-KC的对比

5 结束语

