FD-LSTM:基于大规模系统日志的故障分析模型*

方姣丽,左 克，黄 春，刘 杰，李胜国，卢 凯

(国防科技大学计算机学院，湖南 长沙 410073)

1 引言

在通往E级系统的道路上，可靠性(仅次于并行管理和能源效率)被视为三大挑战之一。为保证系统的可靠性，已有许多容错技术被提出并应用于系统，主要有被动容错与主动容错2种机制。被动容错主要是回滚恢复方法，通过定期保存程序执行现场以及其他重要信息，并在系统发生故障时实施系统恢复，保证程序能够持续正确地运行。而为避免系统发生失效，在故障及差错的潜伏期内及时地发现故障、修复故障或者隔离故障，这就是主动容错机制。相比于被动容错的回滚恢复等方法，大量的研究集中在主动容错的预测故障上，即预测故障的能力，这样就可以在任何故障出现之前采取规避措施。这将允许在系统仍然正常运行的情况下采用缓解机制，从而能够更容易地推理全局应用状态，并降低保存和随后恢复数据的昂贵成本。

本文使用我国某大规模计算系统投产后的作业故障日志信息，对日志信息进行分析处理，设计实现故障分析模型FD-LSTM(Fault Diagnosis-Long Short-Term Memory)，主要工作有：(1)分析处理该大规模计算系统的日志信息，得到系统的故障时间分布特性和空间分布特性，并与国外系统的故障时空分布特性进行了对比；(2)由于系统的故障类型包括软件故障、硬件故障、人为故障及不明原因的各种故障，采用K-Means方法对故障进行聚类，并分析了每种故障类型的特点；(3)结合故障类型、故障日志时间序列和系统体系结构设计并实现了FD-LSTM模型；(4)通过实验论证了时间预测和空间预测的精度与故障聚类类型相关，聚类结果可以分为2类，一类是与时间相关的故障，比如，由于热和网络的原因引起的故障，另一类则是与时间无关的故障，比如纯硬件故障的单结点内存硬件故障。实验结果表明，与时间相关的故障类型，基于LSTM进行故障发生时间和故障结点位置的预测效果较好。故障发生时间预测的RMSE(Root Mean Square Error)可低至0.461，同时，对故障发生的结点位置号cn进行预测，预测精度可达80.56%。

2 相关研究技术

2.1 故障分析技术

故障预测是一个被广泛研究的领域。目前，已有众多方法用来实现故障预测，这些方法大致可以分为3类:(1)基于故障机理PoF(Physics-of-Failure)的方法，PoF是一种根据故障发生的内在机制和根本原因进行间接预测的方法；(2)数据驱动DD(Data-Driven)的方法，DD是一种应用统计学或者机器学习等技术手段对可靠性指标进行直接预测的方法；(3)融合的方法，这种方法是前2种方法的结合[1]。近年来，数据驱动的方法由于其便捷性和高效性等特点，在实际可靠性预测中的应用日渐广泛。

故障时间序列是一个重要的可靠性指标，能够展示故障的动态演化过程，对系统故障的预测可以通过对故障时间序列的预测来实现。通过对故障预测领域实践状况的全面调查可知，故障时间序列目前已经可以被多种数据驱动的方法预测，可以用二维矩阵(如表1所示)来分析研究现状[2]，包括：(1)被预测的故障类型；(2)所使用的预测方法。

Table 1 Failure prediction in high-performance computing systems (accuracy/recall value in %)表1 高性能计算系统中的故障预测(精度/召回值以%为单位)

说明：

加了底纹的文字显示了预测此类故障的能力；

上标A：不同数据集的结果；

上标B:不同训练参数的结果；

上标C：不同参数的结果差异很大；

上标D：论文列出了几种方法或设置；

上标*：提供了许多结果，请见参考文献；

-：未给出数值结果。

表1中的水平维度对故障进行分类，从而显示出有哪些故障。SW/S代表软件或系统故障，Node代表硬件故障，在这2种情况下，故障的根本原因都是不确定的(不是精确的)。精确的故障预测可以分为磁盘Disk、内存和网络故障预测。由于内存和网络故障没有预测精度和召回值，故没有列出，而GPU故障预测工作非常有限，也略去。水平维度的日志类表示的是通过系统日志来预测即将发生的故障的方法。

表1所列的方法要么需要复杂的特征提取，要么无法捕获长期的依赖关系，难以适应系统规模；同时，这些方法没有对故障的发生时间进行有效预测，并且也不是所有方法都给出了某一确定故障类型的预测结果。最近 Coates 等人[24]证明，大规模的训练可以通过在HPC基础架构上的深度学习来完成，具有可接受的分类性能和可伸缩的效率。

2.2 长短时记忆网络(LSTM)

循环神经网络RNN(Recurrent Neural Network)对较长时间序列的处理效果不理想，原因之一就是无法记住长距离之前的信息，而LSTM 网络通过引入一组存储器单元，允许网络学习何时忘记历史信息以及何时用新信息更新存储器单元，可以很好地处理时间敏感的数据, 成功地解决了原始循环神经网络中存在的问题。LSTM可以随着时间的推移而忘记或重新学习，使其成为了较其他 RNNs 如 Logit模型和多层感知机更好的选择。最近有关利用日志数据对故障发生时间和故障位置进行预测的研究成果有Das等人[25]完成的Desh。其研究表明可以使用0.5的阈值来推断结点故障，即当LSTM获得MSE≤0.5时，可以考虑使用预测结果来检查故障。由于Desh和本文研究的日志数据记录的故障数据来自于不同的HPC系统，使用的日志数据格式与内容也不相同，因此，本文利用日志数据进行故障预测，以区别于Desh，但本文将利用其研究结果的LSTM阈值来评估预测结果。

3 FD-LSTM

本文构建的FD-LSTM预测模型的整体框架如图1所示，包括输入层、隐藏层、输出层、网络训练和网络预测5个功能模块。输入层负责对原始故障时间序列进行初步处理，包括划分数据集、标准化和数据分割，得到的新故障时间序列X1,X2,…,Xt满足网络输入要求;隐藏层采用如图2所示的 FD-LSTM 细胞搭建循环神经网络；输出层提供预测结果P1,P2,…,Pt;网络训练计算模型输出与理论输出的损失，采用Adam 优化算法;网络预测采用迭代的方法逐点预测,对预测结果反标准化，可以得到与测试集对应的故障发生时间或结点位置。

Figure 1 Overall framework of the FD-LSTM prediction model图1 FD-LSTM 预测模型的整体框架

在图2所示的FD-LSTM隐藏层细胞结构中，从细胞状态ct-1到ct是细胞状态的更新，细胞状态类似于传送带,直接在整个链上运行，只有一些少量的线性交互,信息很容易在上面流转而保持不变。LSTM 通过精心设计的称作为“门”的结构来删除或者增加信息到细胞状态。门是一种让信息选择式通过的方法，包含一个 Sigmoid 神经网络层和一个按位的乘法操作。f、i、o分别表示遗忘门、输入门、输出门。FD-LSTM网络采用 BPTT (Backwards Propagation Through Time)算法进行训练。下面给出FD-LSTM网络的训练过程：

Figure 2 FD-LSTM hidden layer cell structure图2 FD-LSTM隐藏层细胞结构

(1)计算遗忘门的输出值ft。FD-LSTM 的第1步是决定从单元状态中丢弃什么信息，这是通过一个遗忘门实现的。遗忘门的输入是ht-1和xt，输出一个0～1的数值来决定单元状态ct-1中丢弃多少信息，所以该门主要用于控制历史信息的输入，过滤掉没用的信息。遗忘门的计算方法如式(1)所示：

ft=σ(Wf·[ht-1,xt]+bf)

(1)

其中，σ代表Sigmoid 激励函数，Wf代表遗忘门权值矩阵，bf代表偏置向量，xt代表当前时刻的输入数据，ht-1代表FD-LSTM 单元前一时刻的输出值。

(2)计算输入门的值。包含2部分内容:①输入门 Input Gate 的值，也就是决定哪些信息需要更新;②一个 tanh 层生成的向量δ，也就是备选的用来更新的内容。这2部分的计算如式(2)和式(3)所示:

it=σ(Wi·[ht-1,xt]+bi)

(2)

δt=tanh(Wc·[ht-1,xt]+bc)

(3)

其中,Wi是输入门的权值矩阵，bi是当前时刻的偏置向量，tanh 是双曲正切激活函数，Wc，bc分别是计算单元状态的权值矩阵和偏置向量。

(3)更新旧的单元状态。将向量ct-1更新为向量ct，让旧的单元状态和遗忘门的输出ft按元素相乘，丢弃掉不需要的信息，然后加上it·δt组成的新的候选值向量，也就是决定添加多少新的信息到单元状态。更新单元状态的实质就是丢弃旧信息，添加新信息。更新过程如式(4)所示:

ct=ft·ct-1+it·δt

(4)

(4)计算输出门的值。输出门使用 Sigmoid 激活函数确定最终输出哪些信息。然后，单元状态经过 tanh 激活函数，由于 tanh 的输出值在-1～1，所以输出一个元素值为-1～1的向量，并将该向量和输出门的输出按元素相乘，最终确定要输出的信息。计算方法如式(5)和式(6)所示：

ot=σ(Wo·[ht-1,xt]+bo)

(5)

ht=ot*tanh(ct)

(6)

其中,Wo为输出门的权值矩阵，bo为当前时刻的偏置向量，ht为t时刻FD-LSTM 单元的输出，ot为输出门的输出。

(5)反向调整。

FD-LSTM 网络模型参数反向调整使用的是最小化代价函数方法，能够使输出值尽可能逼近目标值。假设RUL(t)为t时刻的RUL真实值，RULest(t)是t时刻的 RUL预测值。FD-LSTM 使用式(7)得到损失函数：

J(t)=∑‖RUL(t)-RULest(t)‖2

(7)

对于FD-LSTM 梯度优化问题，常见的优化算法有 AdaGrad、RMSprop、随机梯度下降法 SGD(Stochastic Gradient Descent) 和适应性动量估计算法Adam(Adaptive moment estimation)等。本文选用Adam算法,该算法是一种有效的基于梯度的随机优化方法，融合了AdaGrad和RMSPro算法的优势，能够对不同参数计算适应性学习率并且占用较少的存储资源。相比于其他随机优化方法，Adam算法在实际应用中整体表现更优[26]。

4 实验设计

聚类分析法是大数据挖掘的主要手段之一。系统的故障类型包括软件故障、硬件故障、人为故障以及不明原因的各种故障，可以使用K-Means对故障类型进行聚类。在使用K-Means对故障进行聚类时，K值的确定方法为手肘法，其核心指标是误差平方和SSE(Sum of the Squared Errors)，其计算表达式为:

(8)

其中，Ci是第i个簇，p是Ci中的样本点，mi是Ci的质心(Ci中所有样本的均值)，SSE是所有样本的聚类误差，代表了聚类效果的好坏。其核心思想是：随着聚类数K的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。当K小于真实聚类数时，由于K的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大；而当K到达真实聚类数时，再增加K所得到的聚合程度会迅速变小，所以SSE的下降幅度会骤减；然后随着K值的继续增大而趋于平缓。也就是说SSE和K的关系图是一个手肘的形状，而这个肘部对应的K值就是数据的真实聚类数。

对数据集进行分析和预处理后，利用sklearn的预处理模块对数据特征中的非数值特征进行编码，接着对所有特征进行归一化处理，然后转化为有监督学习问题。考虑到上一故障的提前时间和故障数据，本文将把监督学习问题作为预测当前故障的提前时间(time-interval)。将聚类后的故障数据集划分为训练集和测试集。为了对模型进行训练，利用数据集的前4/5进行训练，剩下的1/5进行评估。FD-LSTM模型中，隐藏层有50个神经元，输出层有1个神经元(回归问题)，输入变量是一个时间步(t-1)的特征，损失函数采用MAE(Mean Absolute Error)，模型采用50个epochs并且每个batch的大小为72。最后，在fit()函数中设置validation_data参数，记录训练集和测试集的损失，并在完成训练和测试后绘制损失图。

5 结果分析

5.1 数据分析预处理

本节将对某系统故障日志数据进行分析处理，并得到该系统的故障时空分布特性。鉴于Mohammed等人[27]对国外的超大规模计算系统的组件故障分布进行的研究，可以推断两者分布具有相似性，即不符合正态分布。

从某系统取得日志数据文件后，对部分数据文件进行分析处理，调整日志中故障排列顺序，使数据按时间先后顺序排列，由于故障发生时间不确定，同时也为了便于预测故障发生时间，按照数据集中时间先后顺序计算相邻故障发生的时间间隔(单位：s)并保存为time-interval列，排除间隔时间中的异常值后，此时数据集总共有1 048 574行。每个故障结点发生的故障统计数目如图3所示，发生故障的结点数目较多，其中，管理结点(结点编号为mn3，在图3横坐标的最后)的故障发生数目330 429，明显高于其他所有结点的。

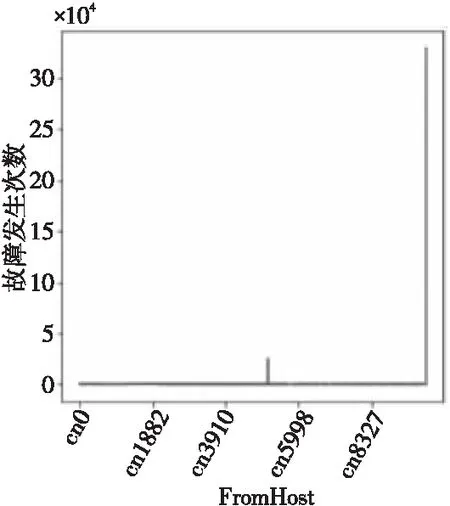
Figure 3 Statistics on the number of times of faulty node failure (including mn3 node)图3 故障结点故障发生次数统计(含mn3结点)

Figure 4 Distribution of system fault space图4 系统故障空间分布

为了得到较好的预测结果，在对故障结点位置进行预测的时候本文暂时不对管理结点进行预测，即除去数据集中管理结点的相关数据，此时数据集总共有718 142行，为便于查看故障空间分布特征，统计该系统每个机柜的故障发生次数，可以得到如图4所示的故障空间分布。通过对故障日志数据的处理，可以验证故障的空间分布不服从正态分布，与Mohammed等人[27]结果(如图4所示)相似。

图5为故障提前时间分布特征，也并非正态分布。经分析故障发生的间隔时间基本在0～20 s。计算各个数值变量之间的相关系数，得到一个5*5矩阵，可用热度图可视化相关系数矩阵，如图6所示。

Figure 5 Time distribution of fault图5 故障发生时间分布

Figure 6 Heat chart of correlation of numerical variables图6 数值变量相关关系热度图

5.2 K-Means聚类

采用手肘法得到如图7所示的K与SSE关系图。显然，肘部对应的K值为3(曲率最高)，故对于这个数据集的聚类而言，最佳聚类数应该选3，聚类结果饼图如图8所示，由此可知，聚类0占比58.28%，聚类1占比22.90%，聚类2占比18.82%。

Figure 7 K-SSE relationship diagram图7 K-SSE关系图

Figure 8 Pie chart of clustering results图8 聚类结果饼图

聚类结果与故障数据特征关系由图9所示的雷达图可知，聚类0故障是最常见的故障，因此聚类统计数目最多，最为频发，聚类1故障在故障位置和故障校验码上的特征最为明显，相比于聚类0的故障，聚类1的故障发生频率较低，因此可以判断，聚类1中严重程度较高的故障数高于聚类0的，而聚类2中严重程度较高的故障数最多，频发度最低。

Figure 9 Cluster radar chart图9 聚类雷达图

对故障数据及聚类后故障类别的故障优先级进行统计，可以验证前述推断，故障优先级越高，故障严重程度越低。其统计图如图10所示，具体故障优先级对应数目如表2所示。本文在取得日志故障数据后，去除管理结点故障日志数据后有718 142条数据，其中，故障优先级为5和7的故障均为管理结点的故障优先级，因此，表2中无优先级为5和7的故障。在进行K-Means聚类时，数据预处理剔除了极少数异常数据。

Figure 10 Detailed fault priority ranking图10 详细故障优先级分级

Table 2 Detailed fault priority ranking

5.3 FD-LSTM

HPC系统在硬件、软件和应用程序层面上会发生各种各样的故障，包括由于电源不良、网络接口卡出现故障或无法解释的重启等结点故障，以及对并行文件系统的写入失败故障，需要从并行文件系统重新启动的不常见硬件故障，工作停止了进展但没有失败的工作挂起故障，以及由于浮点异常或由于瞬态处理器故障导致的内存分段违规的作业失败故障等等[27]。利用K-Means聚类的故障分类结果，分别对故障聚类基于FD-LSTM进行故障预测，可以从模型预测结果判断故障聚类类型是否与时间相关。

5.3.1 故障发生时间的预测

利用FD-LSTM模型，对K-Means聚类的每个类别进行单独的故障发生时间预测测试后绘制的损失图如图11所示。从训练与测试损失折线图可以明显看出，基于K-Means聚类的FD-LSTM故障预测效果要优于初始故障预测。

Figure 11 Chart of predicting training and test loss图11 故障发生时间预测训练与测试损失图

基于FD-LSTM对各个类别进行故障发生时间预测的RMSE如表3所示。

Table 3 RMSE based on FD-LSTM time prediction for each category表3 基于FD-LSTM的各类别故障发生时间预测的RMSE

聚类2类故障发生时间实际预测结果最好，聚类1的最差。由于某一故障发生后，受其影响结点编号(cn号)很可能不是单一的，故而，在某一结点发生故障后，在几乎没有提前时间的情况下也很可能会相继有几个结点发生故障，因此实际很多故障发生时间极短，而预测得到的发生时间很多也极短。

5.3.2 故障结点位置预测

通过上述对故障提前时间的预测可知，故障聚类类别2的时间相关关系更加密切，因此对聚类类别进行单独的故障结点位置cn号预测，预测测试后绘制损失图如图12a所示。为与之对比，再对聚类类别1进行故障结点位置cn号预测，从训练与测试损失折线图可以看出，聚类2拟合得更好。统计分析通过聚类2对故障的发生结点位置进行预测的结果，通过式(9)计算预测精度Precission：

Precission=TP/(TP+FP)

(9)

由于现在的分簇结构一般是4个cn号位于一个簇内，而簇内是共享内存和网络的，也就是说，簇内任意一个结点发生故障，整个簇都需要更换。因此，TP包含正确预测的故障结点cn号及同簇结点cn号的数目。FD是错误预测的故障数目计算得到的聚类2的精度为80.56%。

Figure 12 Chart of node fault location prediction training and test loss图12 结点故障位置预测训练与测试损失图

6 结束语

研究人员一致认为，故障预测即使不完美，精度有限，但还是有用的。假设50%的结点故障被正确预测，而剩下的结点故障被错误预测(假阳性)，那么就可以避免一半昂贵的检查点/重新启动，这需要通过更廉价的进程迁移进行全局协调[25]。

通过本文前述研究可以得知，系统故障的时空分布特性都不符合正态分布，故本文设计并实现了FD-LSTM，相比经典LSTM，它更适用于基于故障日志时间序列的故障预测中。本文使用K-Means对故障类型进行聚类，聚类结果可以分为两大类：一类为与时间相关的故障类型，比如，由于热和网络的原因引起的故障；另一类是与时间无关的故障类型，比如纯硬件故障的单结点内存硬件故障。实验结果表明，与时间相关的故障类型，基于FD-LSTM进行故障发生时间和故障结点位置的预测效果较好。故障发生时间预测的RMSE可低达0.461。对故障发生的结点位置进行预测，预测精度可达80.56%。

本文对故障发生时间与发生位置的预测是相对独立的，目前有利用LSTM和事物的时空关系进行的研究[28],接下来可以考虑联合故障时空信息对故障进行预测。为了充分挖掘和利用数据信息，Wang等人[29]使用Bi-LSTM取得了很好的研究效果，因此未来的工作可以考虑使用双向LSTM。大规模计算系统的故障日志数据收集难度较大，收集而来的故障日志数据需要进行复杂的清洗处理，而故障随时会产生，因此日志数据是在不断生成的，目前也不能做到因果推理，在未来的工作中，还可以对日志进行NLP分析，研究分析如何做到在线演化和因果推理，得到故障传播模型等。