一类三重或四重线性码的构造*
薛文芳,王维琼,李亚伟
(长安大学理学院,陕西 西安 710064)
1 引言
设p为素数,m为正整数,q=pm,Fq表示具有q个元素的有限域。Fp上的一个[n,k,d]线性码C为Fp上n维向量空间的一个k维子空间,其中d为码C的极小汉明距离,它刻画了线性码C的检错与纠错能力。线性码C的重量计数器可表示为:
1+A1z+A2z2+…+Anzn
(1)
其中,Ai为线性码C中汉明重量为i的码字的个数。若|{Ai|Ai≠0,1≤i≤n}|=t,则称线性码C为t重线性码。对于一个参数为[n,k,d]的线性码C,若参数为[n,k,d+1]的线性码不存在,则称线性码C为最优码。若参数为[n,k,d+1]的线性码C最优,则称参数为[n,k,d]的线性码C为几乎最优码。较少重量的线性码可用于构造秘密共享方案、认证码、结合方案及强正则图等。
2007年,Ding等[1]利用有限域上的迹函数提出了一种构造线性码的一般方法。有限域Fp上长度为n的线性码C可由式(2)给出:

∀x∈Fq}
(2)

受文献[14]的启发,本文基于布尔函数构造出了一类二元三重或四重线性码,给出了码的参数和重量分布,所构造出的线性码的对偶码均为关于Sphere-packing界的最优码或几乎最优码。
2 预备知识
本节给出第3节中需要用到的一些定义和引理。
设p为素数,m为正整数,q=pm,Fq表示具有q个元素的有限域。
定义1[15]有限域Fpm到Fps的迹函数定义为:

(3)
其中,s为m的正因子。
定义2[15]对∀a∈Fq,有限域Fq上的加法特征定义为:
(4)
其中,x∈Fq,ζp为有限域Fp上的m阶本原单位根。
若a=1,称χ1为有限域Fq上的典范加法特征。显然χa(x)=χ1(ax)。有限域Fq上加法特征具有如下正交关系:
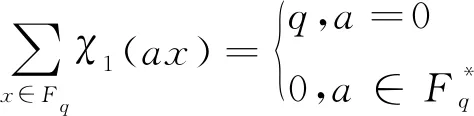
(5)
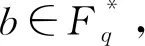
(6)
特别地,当p=2时,对∀a,b∈F2m,令f(x)=ax2h+1+bx,其中正整数h满足1≤h (7) 引理2[16]若m/l为奇数,则: Sh(a,b)=Sh(1,bc-1) (8) 特别地,当a=1时,有: (9) 引理3[16]设e为正整数,若偶数m=2e,且m/l为偶数,则: (10) ①若a∉〈α2l+1〉,则f(x)为Fq上的置换多项式。设x0为f(x)=b2h在F2m上的唯一解,则: (11) ②若a∈〈α2l+1〉,且f(x)=b2h在F2m上无解,则Sh(a,b)=0。若a∈〈α2l+1〉,且f(x)=b2h在F2m上有解,记x0为其中一个解,则: (12) 定义3布尔函数f:F2m→F2的Walsh变换定义为: (13) 定义4[17]设K为有限域Fp上(n,K,d)码C中码字的个数,若: (14) 称码C满足Sphere-packing界。 证明由Walsh变换的定义,有: n=|{x∈F2m|g(x)=1,g(x+α)=0}|= (15) 证毕。 □ (16) 中零码元的个数,则: (17) (18) 其中, 证毕。 □ 本节后面内容考虑以D为定义集的线性码CD。 首先给出g(x)和F(x)的Walsh变换。 引理6g(x)的Walsh变换满足: (19) (20) 引理6的结论的证明可由Walsh变换的定义、引理2和引理3的结论得出。 (21) 证明由Walsh变换的定义和引理1得: (22) (23) 证毕。 □ Table 1 Weight distribution of code CDin theorem 1表1 定理1中码CD的重量分布 证明由引理4和引理7知线性码CD的码长n=2m-2。 (24) w1=2m-3, (25) 由于零码字出现了2次,故线性码的维数k=m-1。 若记线性码CD的非零重量wi对应的频数为Ai(1≤i≤3),则根据MacWilliams方程[18]可得: (26) 解此方程组有: (27) 证毕。 □ 类似定理1中的方法,可得如下结论。 Table 2 Weight distribution of code CDin theorem 2表2 定理2中码CD的重量分布 Table 3 Weight distribution of code CDin theorem 3表3 定理3中码CD的重量分布 Table 4 Weight distribution of code CDin theorem 4表4 定理4中码CD的重量分布 本文利用定义集的方法构造出了一类三重或四重线性码,确定了这些码的参数、重量分布和对偶距离,并编写Magma程序验证了所得结论。 根据文献[3]中的引理13和定理12,若线性码中非零码字的最小重量wmin和最大重量wmax满足关系式: wmin/wmax>(p-1)/p (28)





3 主要结果及证明


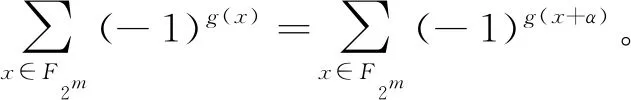









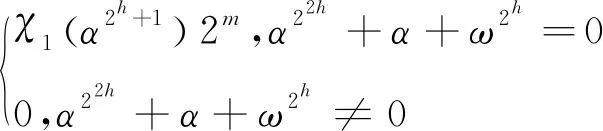
















4 结束语


