基于格林函数方法的核部件疲劳分析方法研究

谢 海，邵雪娇，张毅雄，卢喜丰，艾红雷，白晓明，高世卿

(中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213)

疲劳失效是核电站设备的主要失效模式之一，在核电工程设计中一直备受关注。疲劳损伤可导致核电站设备或管道萌生裂纹并持续扩展，严重情况下将导致冷却剂泄漏等后果。核一级部件出现疲劳失效的原因主要有两种，一种是机械振动产生的机械疲劳，一般发生在回路系统上小支管等部件，另一种是由核电厂运行过程中冷却剂温度和压力变化导致的热疲劳失效，如稳压器波动管热分层效应导致的疲劳失效和一回路主管道上支管流导致的热疲劳失效等。机械振动通常导致高周疲劳，可通过改变结构自身的固有频率来降低出现疲劳失效的风险；而热疲劳通常为低周疲劳，由热疲劳导致的失效通常不易发现而难以防止，因此对热疲劳失效敏感位置进行监测和评估是保证核电厂运行安全的重要手段。

为防止核岛压力边界出现的疲劳失效，设计阶段即从保守的角度对设备和管道进行疲劳计算分析。首先要根据热工水力计算和核电厂运行的经验反馈提出各种设计瞬态，并给出这些瞬态发生的次数。事实上，大部分设计瞬态在波动幅度和发生次数的假设上都具有相当的保守性。其次，由于瞬态发生次序是未知的，因此疲劳分析中只能保守考虑最严厉的瞬态组合方式，进一步增加了分析的保守性。从设计角度，一定的保守性是必要的，但合理挖掘疲劳分析的保守余量将给核电厂的经济性带来好处，而采用实际监测的数据进行疲劳计算可达到这一目的。但采用实际检测数据存在着一定的困难，主要的困难来自于热应力计算：若采用商业有限元软件计算结构热应力场，由于实际冷却剂温度和压力时间历程很长，计算将耗费大量资源而失去了可行性。因此，能否快速计算结构热应力是采用实际监测数据进行疲劳计算的关键所在。

近年来大量研究表明，相对于空气环境中的疲劳寿命，反应堆冷却剂环境下金属的疲劳寿命有显著降低[1-4]，业界对此进行了大量研究并提出两种评价方法，本文采用其中应用较多的环境疲劳修正因子(Fen)对考虑冷却剂环境的疲劳寿命进行评估。

本文将以核电厂一回路主管道支管模型为例，采用格林函数法计算实现快速计算热应力，并用快速傅里叶变换求解其中涉及的卷积过程，以进一步加速热应力计算速度。阐述后续涉及的应力线性化、应力配对、应力极值点选取和考虑环境影响的Fen求解过程，最后以算例验证计算方法的正确性。

1 格林函数方法

在数学理论中，格林函数是一种用于求解有初始条件或边界条件的非齐次微分方程的函数，最早由英国人乔治·格林于1828年提出。经过长期研究和发展，格林函数已成为物理学中的一个重要函数，有时也称为源函数或影响函数。格林函数方法的原理可简单理解为：任意一段时程温度加载都可离散为一系列温度变化，每段温度变化产生一个向前发展的波动，这个波动可以是温度或是应力的波动，而总的温度或应力效果为该时间点之前各段的线性叠加[5-7]：

(1)

若考虑温度冲击td时间后分析位置的应力达到稳定状态，则有：

σT(P,t)=G0(P)(φ(t)-Tref)+

(2)

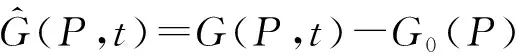
对于一般结构，无法通过解析的方法获取具体点的格林函数，可通过有限元软件计算阶跃热冲击下结构的响应获取关心位置的格林函数[7]。获取格林函数后，通过数值计算积分可获取温度场和应力场。

格林函数法是基于线性叠加理论，而实际计算中材料的物理特性是随温度变化的，这导致了非线性的情况，因此严格来说格林函数法不适用于热应力计算。为从工程上解决这一问题，可保守地采用包络的方法，在生成格林函数时采用最大的Eα(E为弹性模量，α为线膨胀系数)。

2 应力线性化

根据ASME第Ⅲ卷[8]NB-3228.5的要求，当一次加二次应力强度范围Sn超过3Sm时，要对交变应力Sa进行适应性修正，原因是基于弹性力学计算得出的交变应力不能直接用于在S-N曲线上获得许用循环次数，必须进行弹塑性修正。在此过程中需计算评定路径首尾节点的一次加二次应力强度范围Sn，即薄膜加弯曲强度范围，因此需对分析路径的应力进行线性化处理，将沿路径的应力分为薄膜应力σm、弯曲应力σb和峰值应力σp。应力线性化示意图如图1所示。

三维实体单元的应力线性化公式如下。

1) 薄膜应力

(3)

若考虑路径上等距分布的n个点，则可简化为：

(4)

2) 弯曲应力

(5)

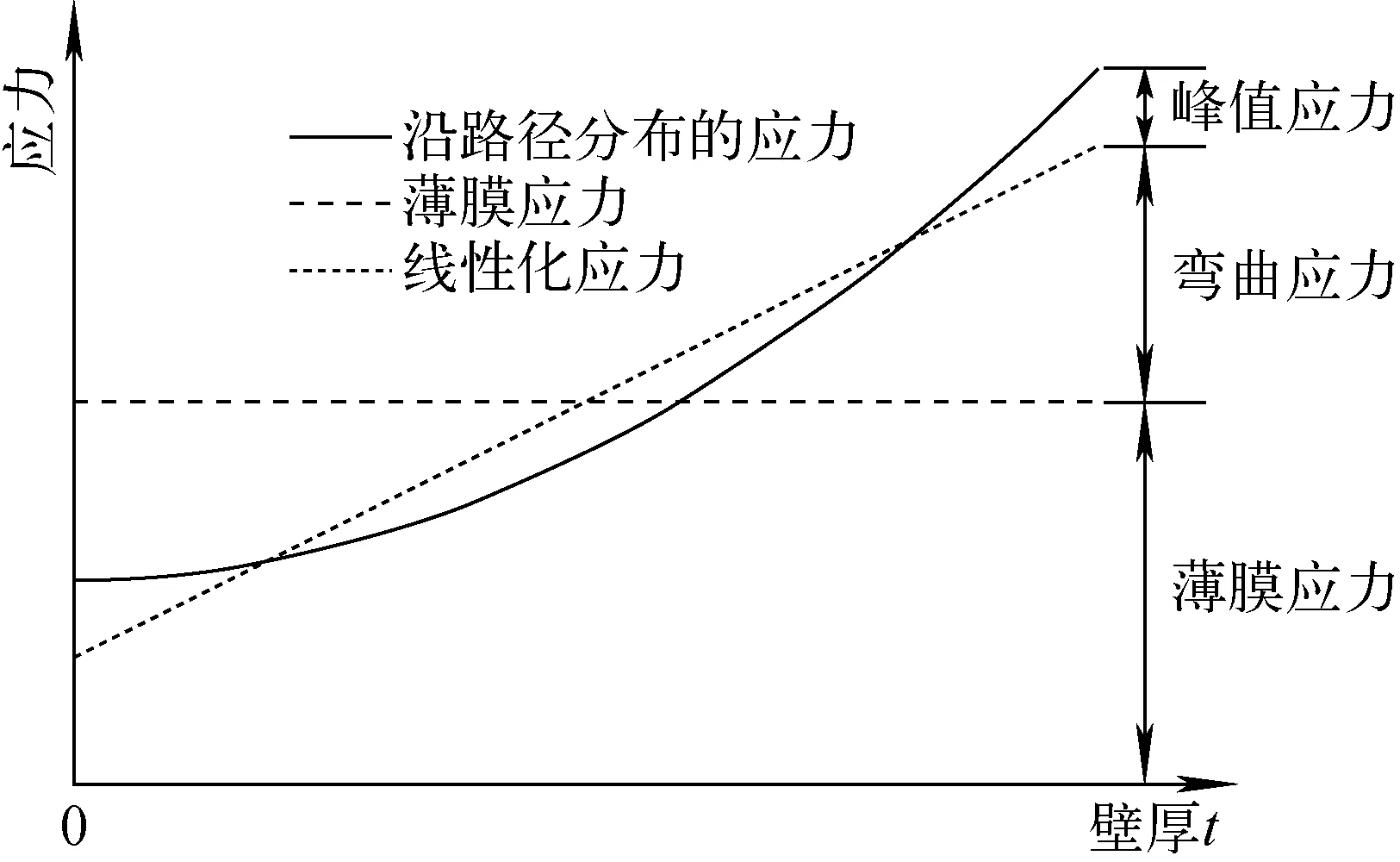
图1 应力线性化示意图Fig.1 Schematic of stress linearization

同样考虑路径上等距分布的n个点，则可简化为：

(6)

3) 峰值应力

(7)

对于二维轴对称情况，应力分量线性化更为复杂，在本文中不进行阐述。从以上公式可看出，为进行应力线性化，需要计算评定路径上若干点的应力分量，本文将计算路径上等距6个点的应力分量。从ANSYS软件说明文档[9]可知，ANSYS在路径上取49个点(包括路径起点和终点)进行应力线性化，为与ANSYS保持一致，本文将6个点的应力分量等距插值成49个点。插值方法可选择分段线性插值或拉格朗日插值，也可选择4次多项式最小二乘法拟合后将起点和终点强制指定为原值。本文将这几种方法的结果与ANSYS进行对比以确定合适的算法。

3 应力极值点选取和应力配对

要确定应力循环应先找出局部的应力极值点，单应力分量(标量)很易找出，但对于多轴应力状态简单的算法不具有可行性。本文拟分别采用两种算法进行极值点搜索，第一种是Rubberband方法(橡皮筋算法)，EPRI在开发FatiguePro4.0时使用了该方法，文献[6]中对该方法已有详细描述并提供了伪代码；另一种是采用Signed tresca stress(带正负号的tresca等效应力)方法，即将tresca等效应力乘以绝对值最大主应力的正负号作为应力时程，再寻找极值时刻点。

由于多轴应力状态的复杂性，选取的应力极值点与其他时间点组合后可能无法得到最大的应力范围，因此文献[6]中采用了Time Window方法(时间窗口方法)，即将极值点前后扩大一定的范围，取极值点附近的一系列时间点代替极值点进行交变应力范围计算，如图2、3所示，范围大小可由材料的疲劳持久极限确定。

图2 极值时刻点在图表上的示意图Fig.2 Schematic of stress extremes

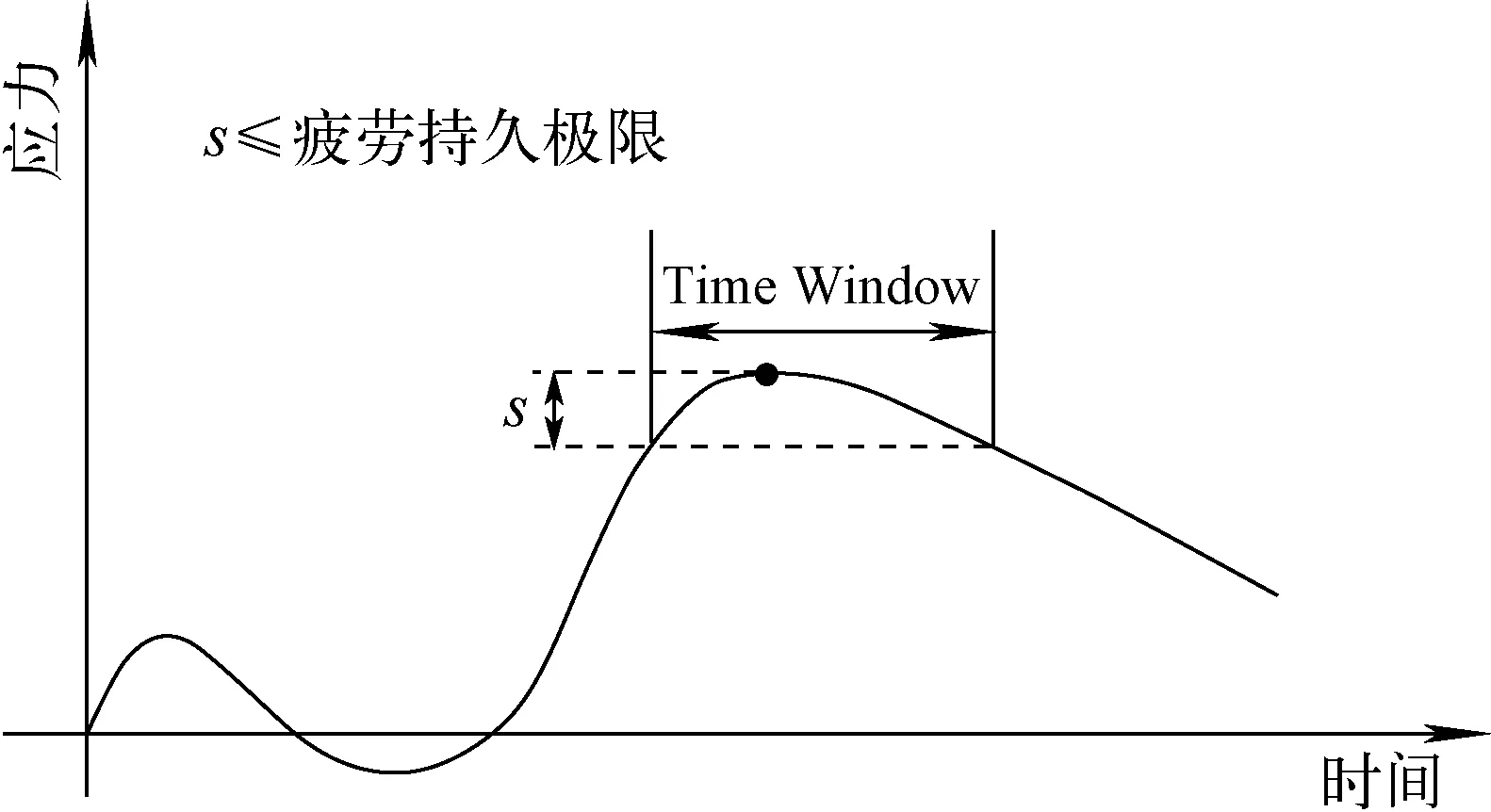
图3 Time Window示意图Fig.3 Schematic of Time Window

获取极值时刻点后应采用雨流计数法进行应力时间点配对，雨流计数法按照ISO-12110-2：2013[10]实现，配对时对累积疲劳使用系数无贡献的波动进行过滤。

4 Fen计算

环境疲劳修正因子Fen是室温下空气中的疲劳寿命Nair,RT与反应堆运行条件下水中的疲劳寿命NPWR之比，即Fen=Nair,RT/NPWR。

根据美国NRC研究文献NUREG/CR6909第1版(2018)[4]，Fen表达式中考虑了冷却剂温度、应变率和水中溶解氧含量的影响，对于低合金钢材料还应考虑材料中硫含量的影响。本文只给出不锈钢材料的Fen表达式：

(8)

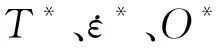
(9)

(10)

对于PWR环境中的水化学情况，有O*=0.29。对于不锈钢，若应变幅值小于0.1%或交变应力小于195 MPa，认为压水堆环境不会导致疲劳寿命降低，因此Fen=1。但当采用修正率方法计算转换应变率时该规定不适用。

(11)

其中：Fen,i为ti-1至ti时刻的Fen；n为1个应力循环之间的总时间步数；Δεi为应变变化量，应变减少时Δεi=0。

5 算例和验证

本文采用核电站典型部件-主管道安注接管作为分析模型，为验证疲劳分析过程涉及的算法，构造了一个包括多个温度变化历程的瞬态，每个变化的幅度随机产生。算例中不包括管道热膨胀等机械外载。

1) 几何、有限元模型和材料

有限元模型如图4所示，模型包括主管道及安注接管，材料为X2CrNiMo18.12(控氮)，材料特性可从RCC-M规范[12]附录ZI中获得。生成格林函数时使用20 ℃的弹性模量和350 ℃下的热导率和线膨胀系数。为使格林函数法计算出的热应力与有限元法结果存在可比性，用有限元法计算瞬态热应力时也采用与生成格林函数时相同的值而不采用随时间变化的材料性能。

图4 有限元模型示意图Fig.4 Finite element model diagram

2) 热格林函数和压力应力传递函数生成

发生安注时安注管内壁面将承受安注水的温度，安注水进入主管道与冷却剂搅混，严格来说主管道流动方向下游将承受搅混后的冷却剂温度，该温度可通过CFD软件计算得出。但在工程上不会做如此详细的分析，而直接认为主管道内壁仍承受主冷却剂的温度，而支管承受安注水的温度。热边界条件划分如图5所示。

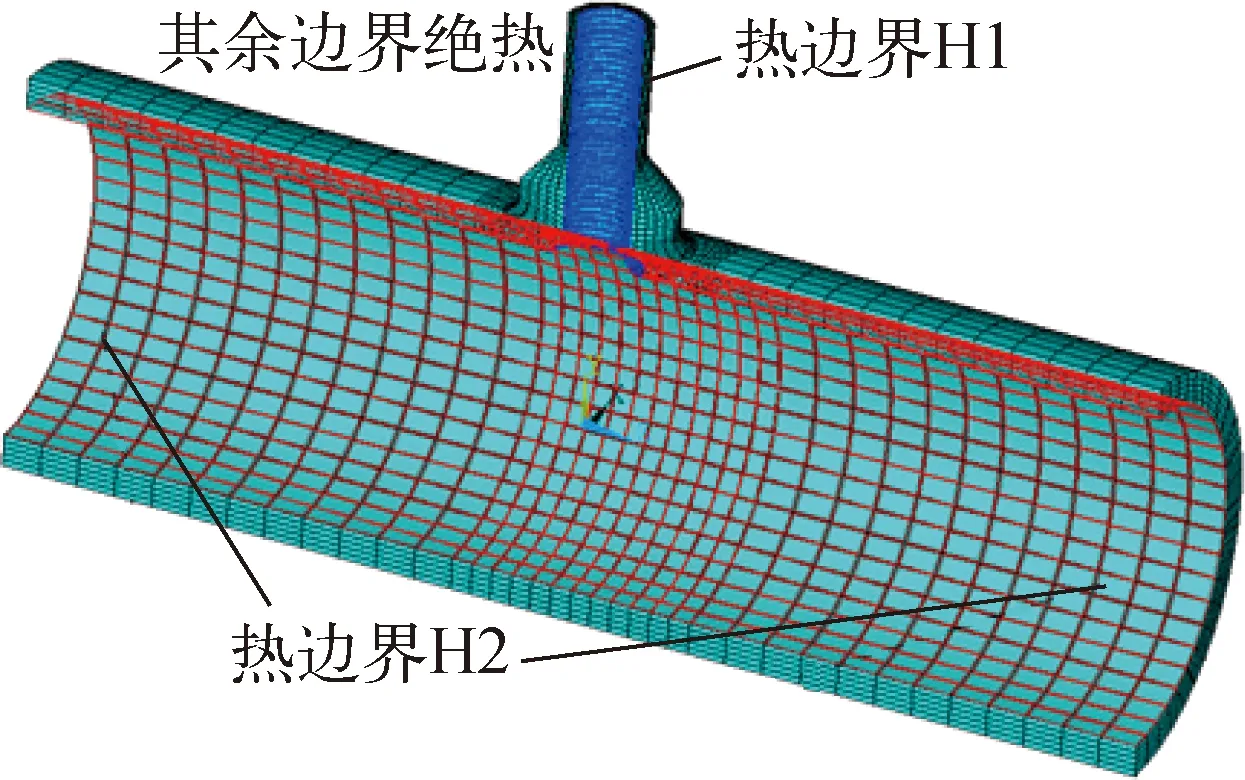
图5 热边界条件Fig.5 Thermal boundary condition

对于存在两个不同边界条件的模型，计算格林函数时应分别施加相应的温度冲击，同时在另一边界施加T=Tref的温度冲击。计算实际热应力场或温度场时，分别计算各自边界承受的瞬态下的值，然后叠加获得实际值。在本例中，取Tref=0 ℃，令图5中热边界H1和热边界H2的热交换系数均为20 kW/(℃·m)，生成格林函数时分别施加0～50 ℃的瞬时温度冲击，同时在另一边界保持T=0 ℃。图6为分析路径内表面节点y方向应力Sy随时间变化的曲线。从图6可见，分析点对两个边界的温度冲击响应不同，由于分析点位于H1边界，因此H1边界对应的格林函数对分析点的影响更大、更迅速。

图6 内表面节点y方向应力Sy随时间的变化Fig.6 y component stress Sy of inner node versus time

本例中压力应力传递函数较为简单，只有1个压力边界条件，在管道内表面施加单位压力并在主管和支管截断面施加等效端头力。

3) 热应力和温度场计算结果对比

施加在主管道和安注接管内壁的温度和压力变化示于图7。为更好地验证算法，假设温度的变化曲线较为极端和随机。

本文采用FORTRAN 95编写格林函数法程序，采用正反快速傅里叶变换求解涉及的圆卷积计算。为应对超长瞬态的情况，采用分段卷积的方法，保证不出现数组大小超出编译器支持的情况。

内表面节点温度格林函数法计算结果和有限元法结果对比如图8所示。从图8可见，格林函数法计算温度场与有限元法结果一致。内表面节点y方向应力Sy的计算结果对比示于图9。从图9可见，热应力计算精度较高，极值点的应力值相差在1%之内，但格林函数法出现极值点的时刻相比有限元法略有滞后，对疲劳计算的影响可忽略不计。

从计算时间看，格林函数法的计算时间主要受瞬态总时长影响，本例中瞬态总时长为336 000 s，且有2个热边界，需分别计算热应力再进行叠加。由于采用了计算圆卷积代替直

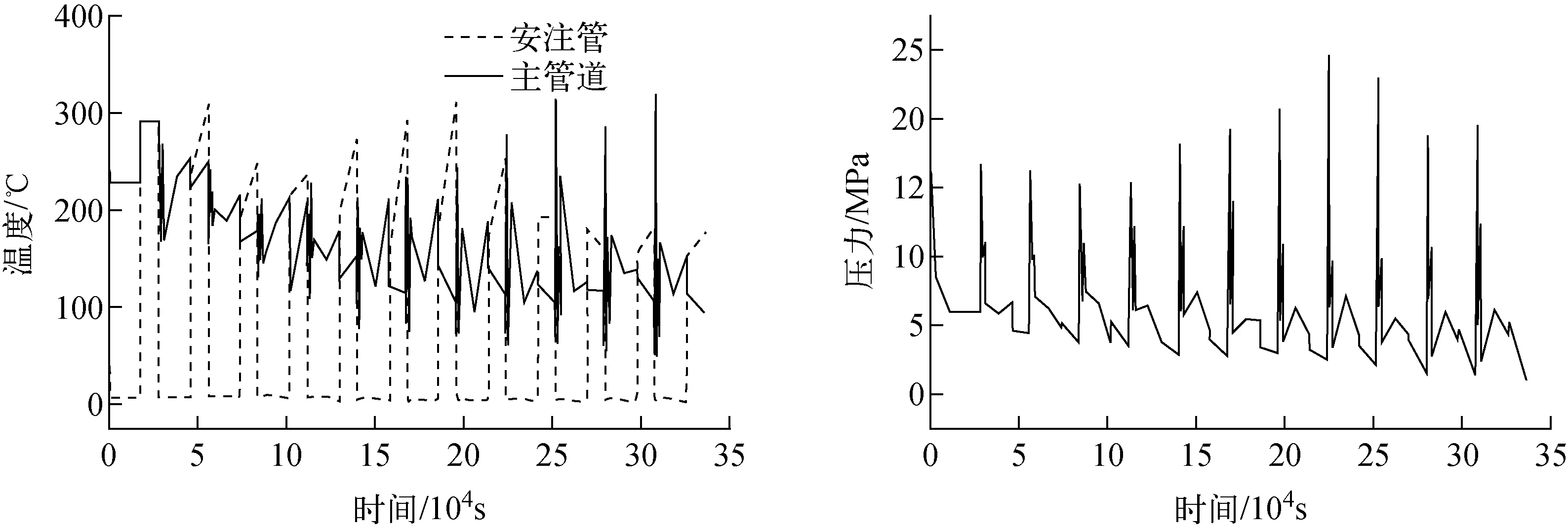
图7 测试算例冷却剂温度和压力时间历程Fig.7 Coolant temperature and pressure history of test case

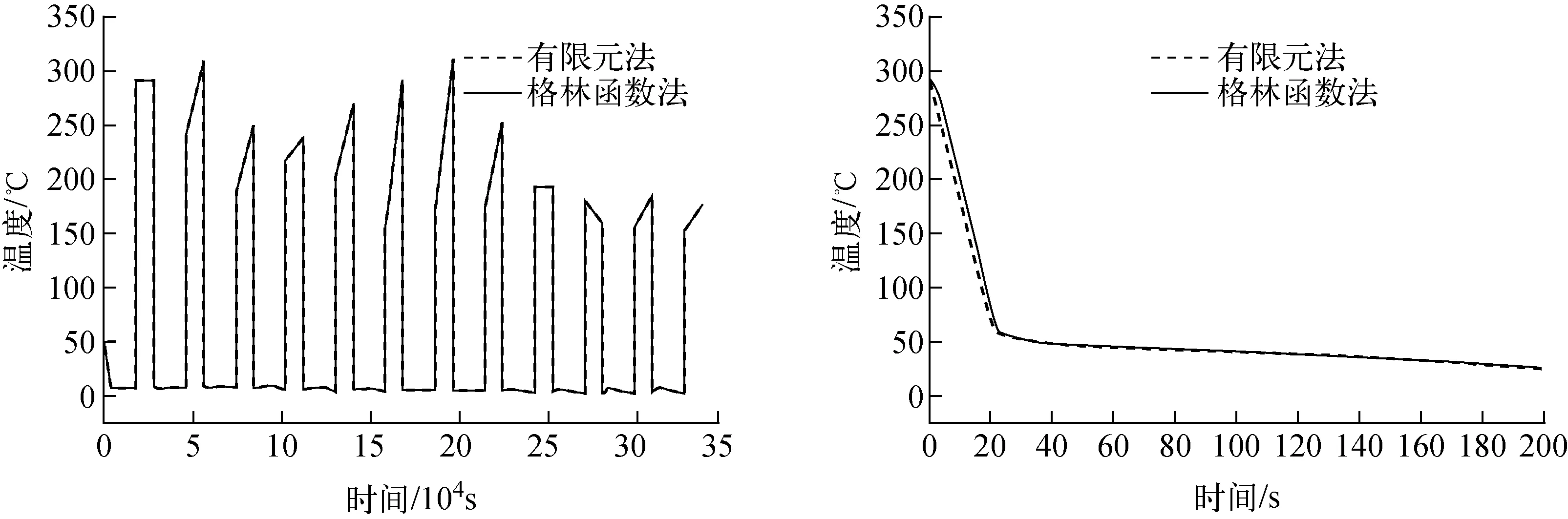
图8 内表面节点温度对比Fig.8 Comparison of inner node temperature

图9 内表面节点Sy对比Fig.9 Comparison of Sy of inner node

接计算线卷积的方法，热应力计算小于10 s。采用有限元软件计算热应力的时间长短主要由计算模型规模、总计算步长和模型复杂程度决定，本例中计算模型规模仅为不足20 000个8节点三维实体单元，采用顺序耦合的方法，总计算步数为800(包括30个计算步，共800个计算子步)，采用惠普工作站HPZ840(Intel Xeon E5-2687W V3+96G内存)，使用8核SMP方式和Sparse Direct Solver(INCORE)，最终计算时间约为147 min。

4) 应力线性化结果对比

在本算例中，计算了沿路径6个节点的应力，并分别采用分段线性插值、拉格朗日插值或4次多项式最小二乘法拟合后将起点和终点强制指定为原值的方法进行应力线性化，将6个点的数据处理为49个点的数据。从本质上来说，只有6个点的数据进行线性化无法获得与ANSYS完全一致的结果，只能在3种方法中找出误差最小的算法。

按3种方法对沿路径应力进行插值后对比，由于格林函数法计算的结果相比有限元法有所滞后，只有都选取极值时刻的值有比较意义，故有限元法选取t=20 s，而格林函数法取t=23 s的结果。线性化结果列于表1。线性化结果仅用于Sn(即σm+σb)的计算(图10)，因此选择拉格朗日插值更为合适。本文仅给出了1个时刻的线性化结果，其他时刻可能出现不同的结论。

表1 线性化应力结果对比Table 1 Comparison of linearization

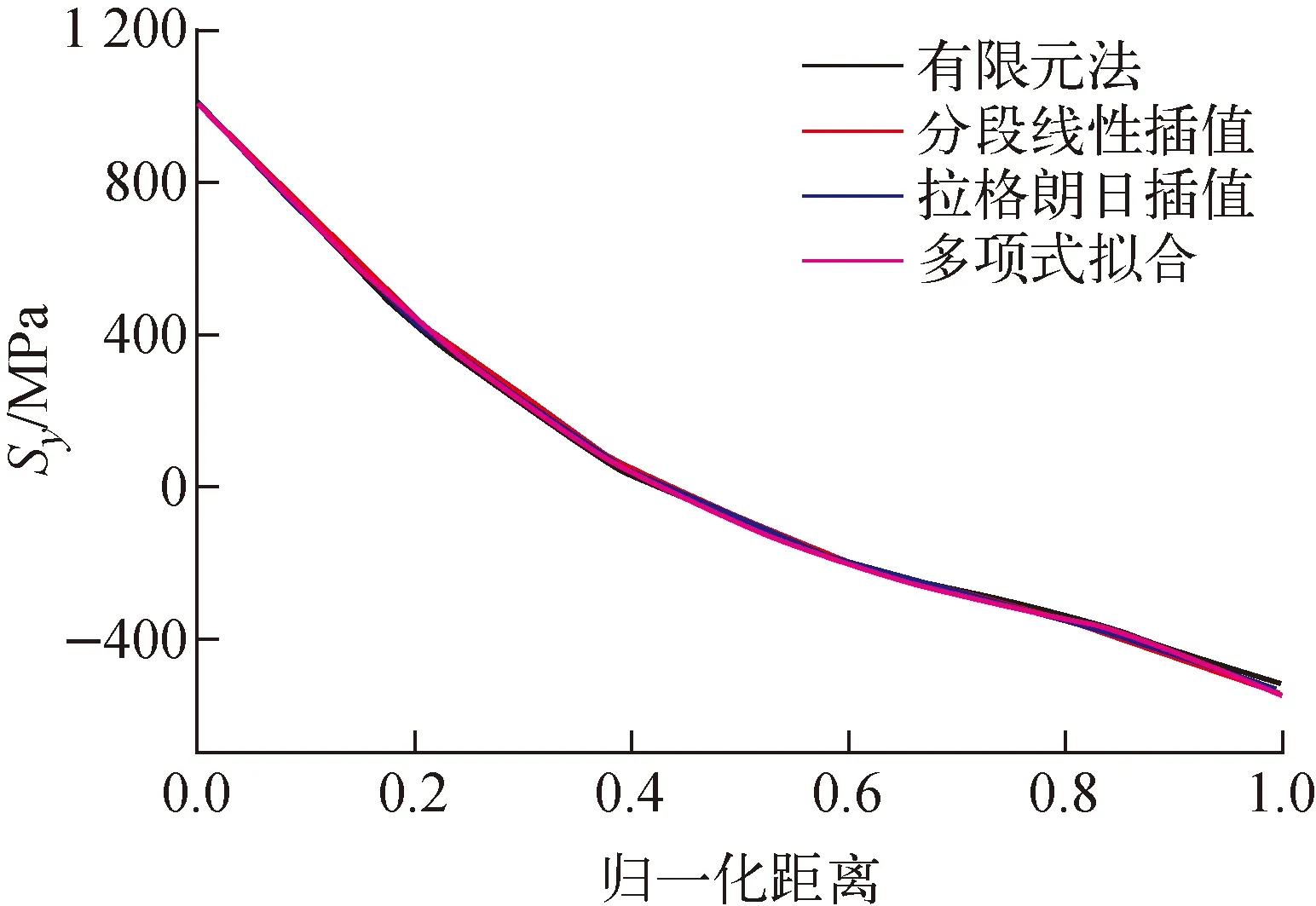
图10 线性化应力结果对比(t=23 s)Fig.10 Comparison of stress linearization results (t=23 s)

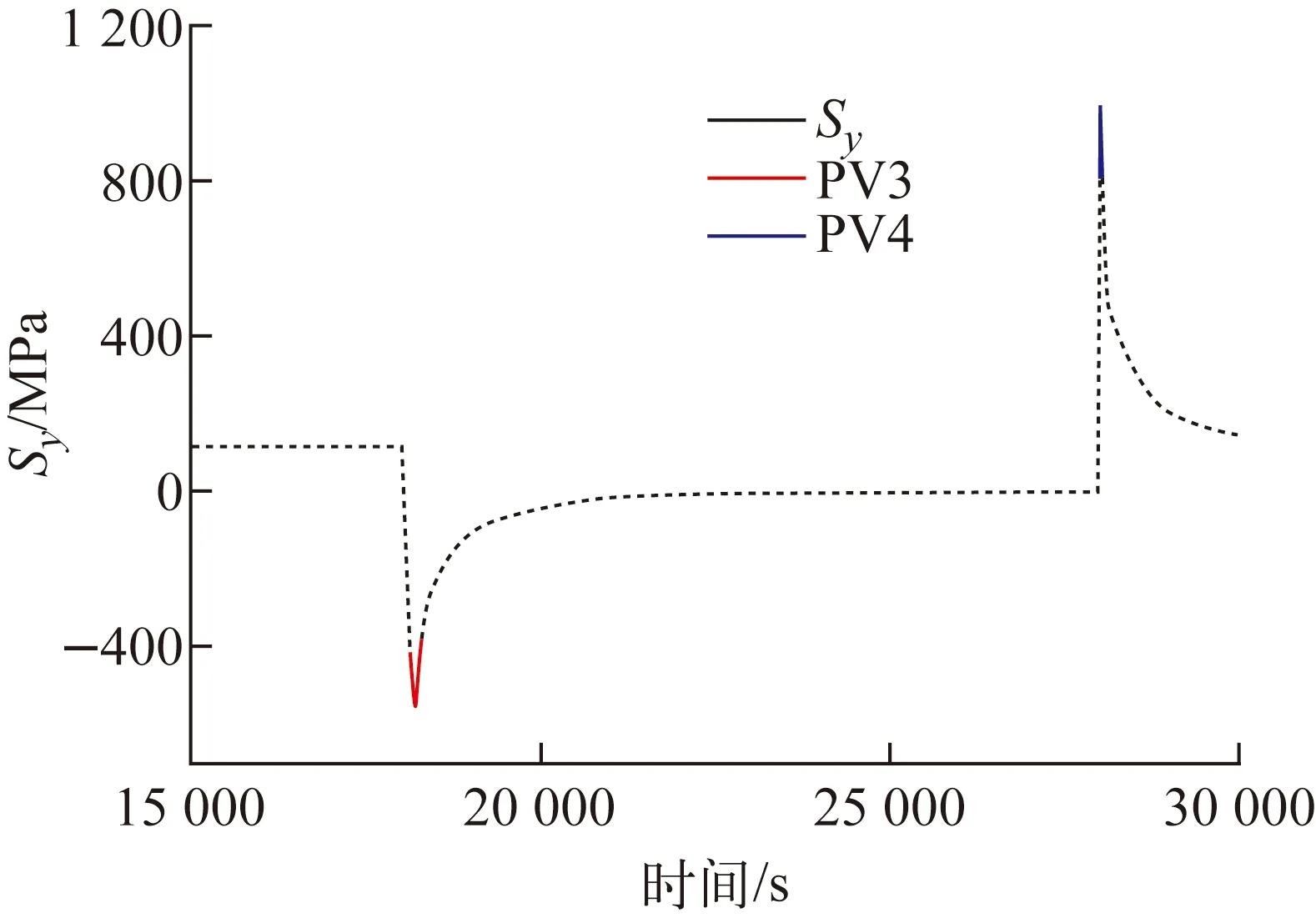
图11 应力极值点查找示意图(第3和第4极值点)Fig.11 Schematic of stress extremes searching (the third and fourth extreme point)

5) 应力极值点查找和应力配对

根据Rubberband算法和Signed tresca stress算法编写了相应的FORTRAN程序，并根据ISO-12110-2：2013实现了雨流计数。ANSYS等商业软件不具备相应的功能，无法进行对比，图11为根据两种算法找出的应力极值点示意图，表2为找出的应力极值点，表3为根据执行雨流计数法程序后的应力配对结果。在本例中，两种方法的结果一致。

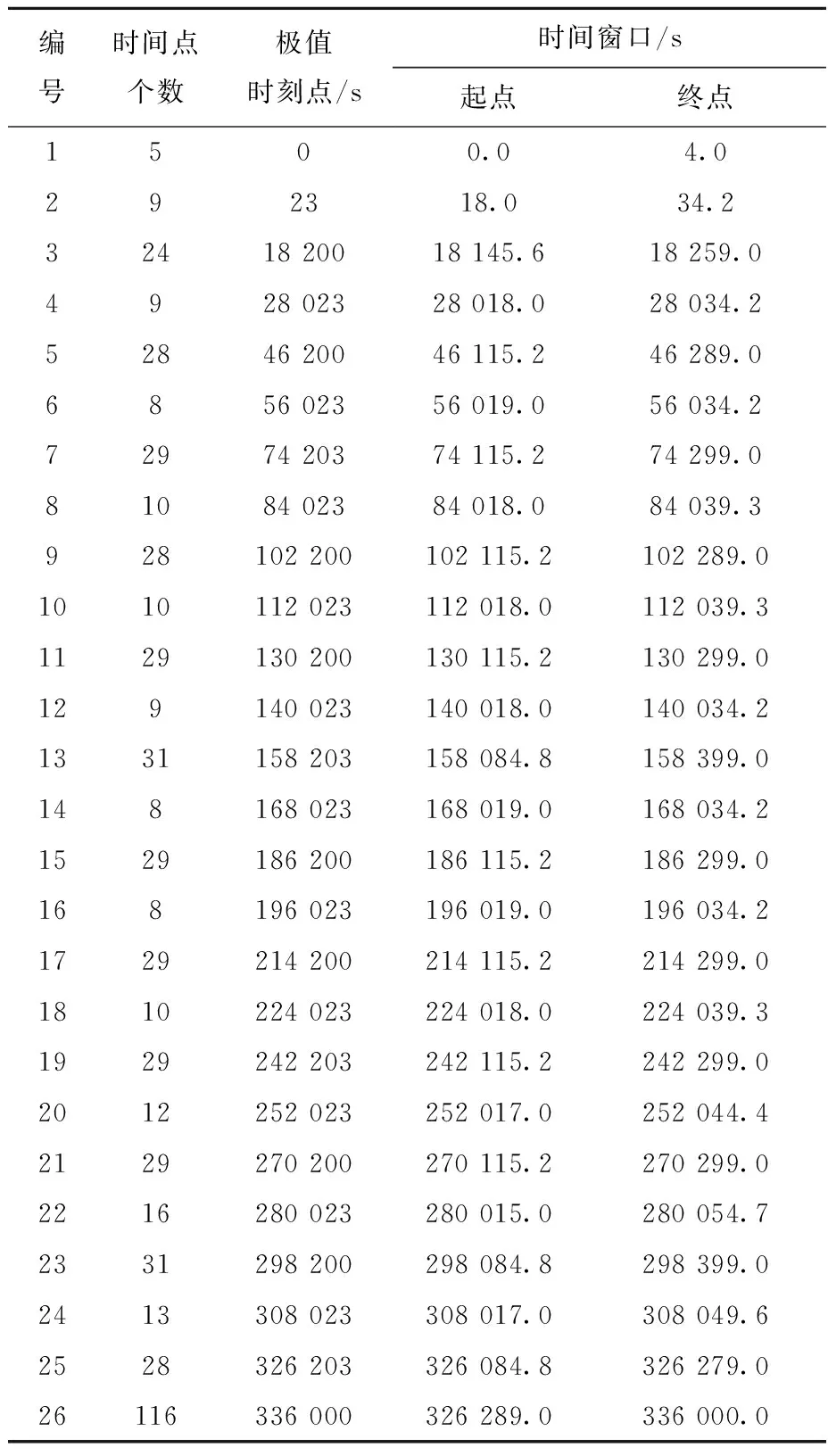
表2 应力极值点查找结果Table 2 Result of stress extremes searching

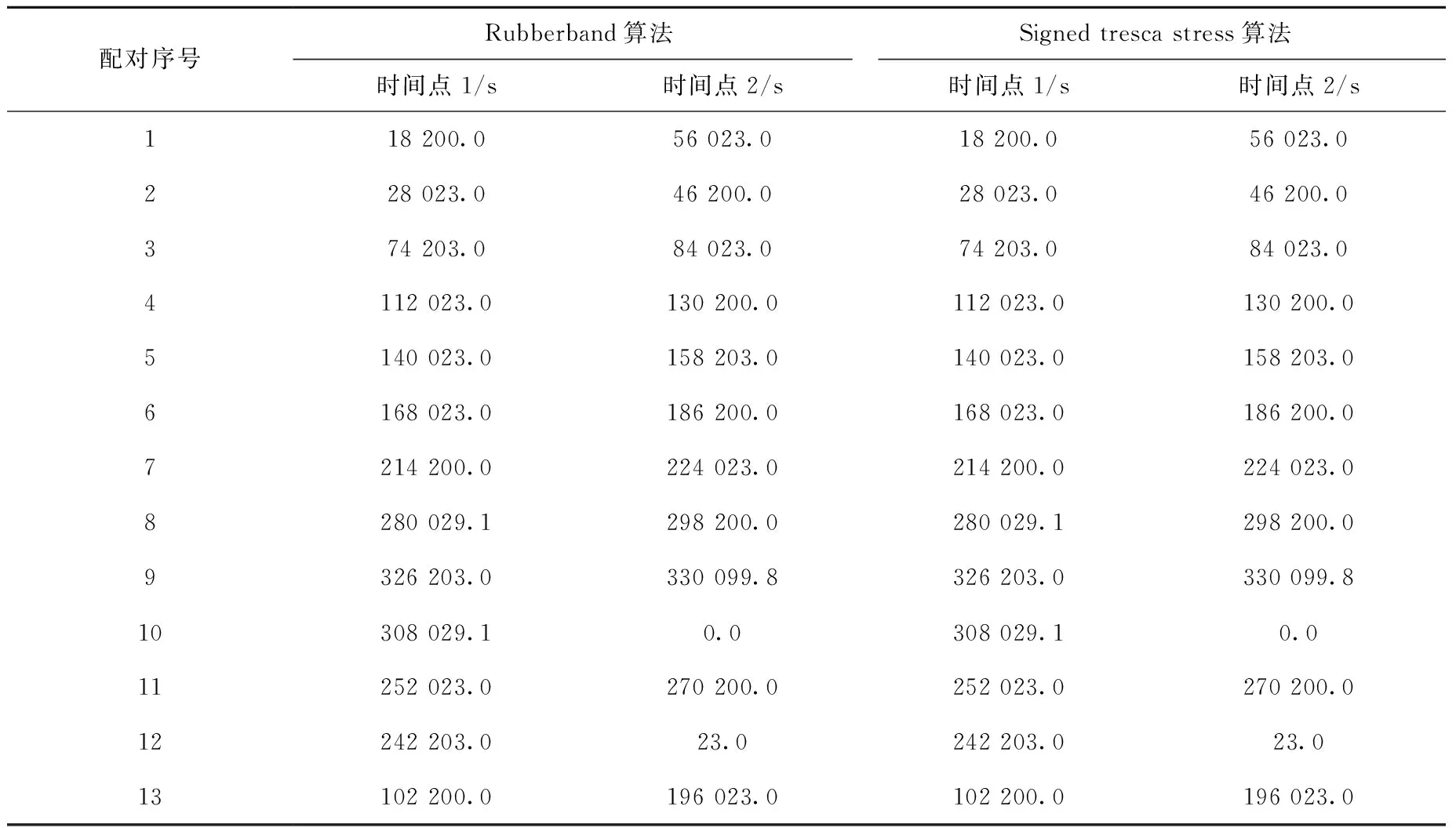
表3 两种算法应力配对结果对比Table 3 Comparison of stress state pairing by two algorithms

6)Fen计算和疲劳使用系数结果

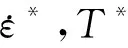
计算Fen时，由于已找出所有应力极值点并进行了配对，只需根据每对组合的时间历程选取对应时间范围的Δε和Fen,iΔε，即可计算出该组合的Fen。图12为正确选取所需计算范围的示意图。如图12a所示，当组合的两个时间点中间相隔多个应力极值点时，只需积分部分区域，如t1至t1下一个峰值点，t2前一个谷值点至t2时刻。如图12b所示，当t1至t2中间不存在其他极值点但应变减少时，积分区域不包括下降区域。

表4为累积疲劳使用系数计算结果。最终结果不考虑EAF的累积疲劳使用系数时为CUF=∑PUi=0.268，考虑EAF时则为CUFen=∑(PUi·Fen,i)=0.534。

6 结论和展望

从以上对比结果可看出，在不考虑非线性因素的情况下，格林函数法用于计算热应力精确度较高，计算速度和所需的存储空间相比有限元法优势巨大，且随着模型的增加优势越明显。本文采用FORTRAN语言编制格林函数法计算热应力程序，并利用正反快速傅里叶变换加速计算速度，极大减少了其中数值积分所需时间。疲劳分析后续涉及的应力线性化、应力极值点查找、雨流计数法配对和计算Fen流程等都已用FORTRAN程序实现，与有限元法的对比结果很好地证明了算法和程序的正确性。

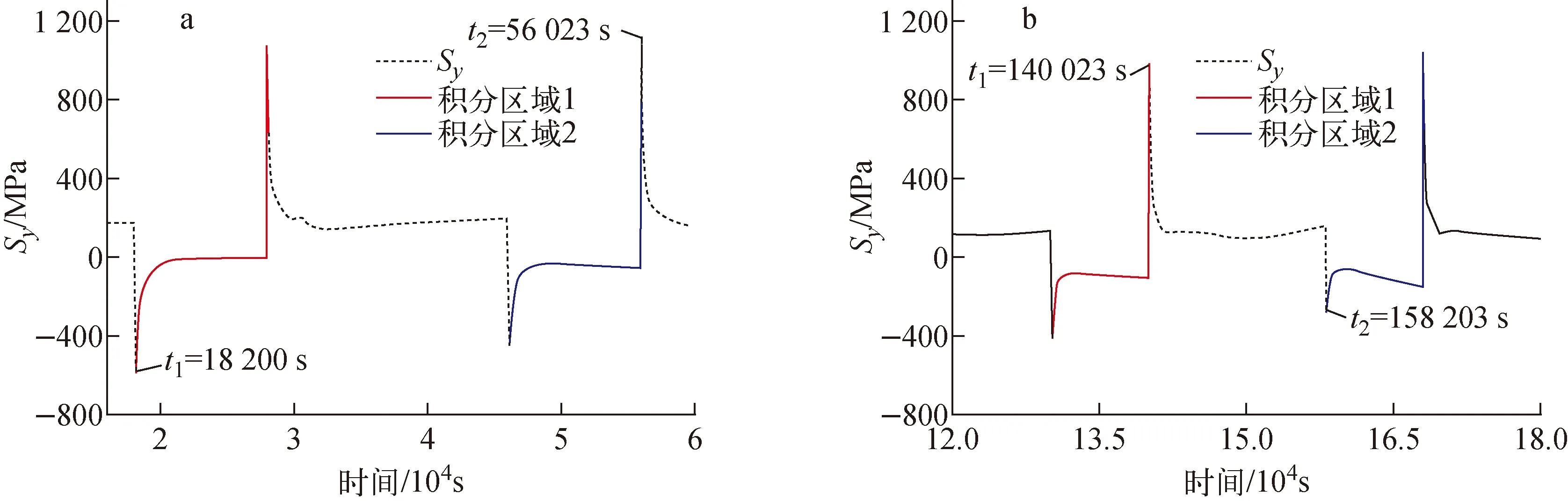
图12 计算Fen积分区域示意图Fig.12 Schematic of integral zone for Fen

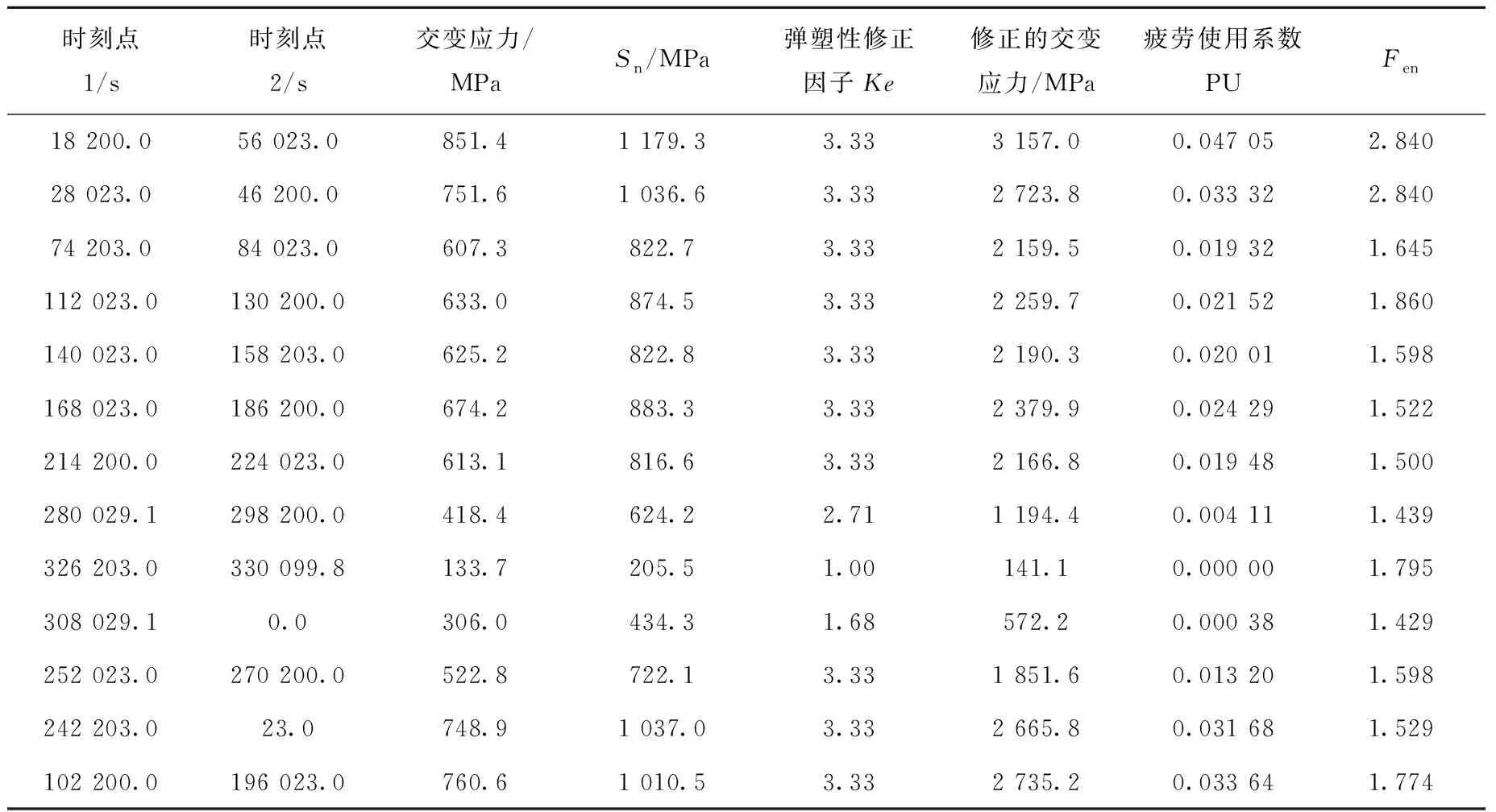
表4 疲劳使用系数计算结果Table 4 Calculation result of fatigue usage factor

但同时也必须看到，由于无法处理热应力计算中的非线性因素，在实际工程中格林函数法具有一定的局限性。对于非线性因素不显著的情况，格林函数法可快速、高效地计算出热应力，为疲劳分析提供数据。为解决格林函数法无法应对非线性因素的问题，近年来已有部分学者通过权系数等方法对格林函数进行修正来解决该问题[13-15]，但生成对应权系数的方法并不简单，后续的研究可从这方面着手，进一步提高格林函数法在实际工程中的应用价值。