强背景噪声下反应堆内冲击信号的特征提取

朱少民，夏 虹,*，杨 波，王志超，彭彬森，姜莹莹，张汲宇

(1.工业和信息化部 核安全与先进核能技术重点实验室，黑龙江 哈尔滨 150001；2.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001)

松动部件是指反应堆内由于损坏、腐蚀和老化等原因导致松动和脱落的部件，同时还包括换料、检修等维护过程中引入的外来物，如螺栓、螺母、线圈弹簧片等。松动部件可能会对堆芯、蒸汽发生器和主泵造成损坏，从而引起严重事故。松动部件监测系统(LPMS)的主要功能是对反应堆主冷却剂系统内的金属松动部件进行连续监测，并在探测到松动部件冲击后，对其质量、位置等信息进行评估[1-2]。根据美国ASME OM-S/G—2007标准，压力容器上、下部各安装3个间隔120°分布的加速度传感器，实现对反应堆内松动部件冲击的实时监测。但从运行经验来看，高误报率和漏报率是LPMS普遍存在的问题[3]。其中一个原因是由于各种设备的运行和高压冷却剂的流动，使得LPMS所获取的信号混合有很强的背景噪声。噪声的影响使冲击信号的监测变得更加困难，并降低了后续质量估计和定位分析的精度。

如何有效地从噪声中提取出信号的冲击特征已成为反应堆监测领域的热点问题，采用的方法主要有小波变换(WT)[4]、小波包变换(WPT)[5]、盲源分离[6]、近似熵[7]等。但在背景噪声较强的情况下，可能会导致算法性能下降，提取特征不明显。针对该问题，本文提出一种基于VMD(变分模态分解)和WPT相结合的特征提取方法。首先采用VMD算法将含噪声的冲击信号分解为一系列不同频率成分的本征模态函数(IMF)，并基于峭度和相关系数构建加权峭度指标作为VMD分解后信号重构的依据，然后发挥WPT频率分辨率高的优势对重构信号进行去噪。

1 基本理论

1.1 VMD

VMD是一种新的信号自适应分解方法，它能将信号分解为一系列模态分量并通过迭代确定每个分量的中心频率和带宽[8]，能有效抑制经验模态分解(EMD)过程中存在的模态混叠和端点效应等问题。

每个模态分量都具有中心频率和有限带宽，VMD的分解过程就是求解K个模态函数μk(t)，k∈{1，2，…，K}，使其估计带宽之和最小，且各模态函数之和为输入信号f(t)，因此，利用VMD对信号进行分解的过程就可用式(1)所示的约束变分模型表示。

(1)

式中：μk(t)为各模态函数；ωk为各模态函数的中心频率；δ(t)为冲激函数。

为求解上述的约束变分问题，引入二次惩罚因子α和Lagrange乘法算子λ(t)。其中α可保证在高斯噪声存在的情况下信号重构的精度，λ(t)可保证约束条件的严密性，则扩展的Lagrange表达式如式(2)所示。

L(μk(t),ωk,λ(t))=

(2)

在振动信号分析和特征提取的各类度量指标中，峭度和相关系数是两个重要的指标并得到了广泛的应用。峭度对振动信号中的冲击分量极为敏感，峭度值大的模态分量中包含有更多的冲击成分，对这些分量进行重构，重构后的信号会包含有更明显的冲击特征。但峭度只依赖冲击信号的分布密度，有可能会忽略一些振幅较大但分布较分散的冲击分量。相关系数可表征信号间的相似程度，但在冲击信号检测中易受到噪声的影响。因此，考虑到这两个指标的优缺点，构建加权峭度指标作为VMD分解后选取IMF进行信号重构的依据，加权峭度指标KCI定义如下。

KCI=KI·|C|

(3)

(4)

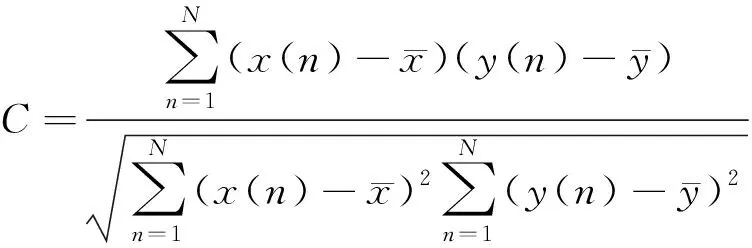
(5)

式中：KI为信号序列x(n)零均值下的峭度值；N为信号长度；C为信号x(n)和y(n)之间的相关系数，文中表示各IMF与原始信号之间的相关系数，其取值范围为|C|≤1。

1.2 WPT

WPT继承了小波变换良好的时频局部化优点，能对信号在全频带内进行多分辨率分解，对低、高频部分都能进行细化处理，克服了小波变换频率分辨率不高的缺点。WPT的分解算法如式(6)所示。

(6)

WPT的重构算法如式(7)所示。

(7)

式中：d为小波包分解系数；h、g分别为高通和低通滤波器系数；l、k为分解层数；j、n为小波包节点号。1个3层的小波包分解过程如图1所示，其中S表示原始信号，A表示低频部分，D表示高频部分。

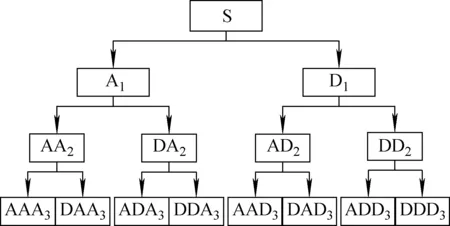
图1 3层小波包分解示意图Fig.1 Schematic diagram of 3-layer wavelet packet decomposition

由图1可知，原始信号S经过3层小波包分解后可表示为：

S=AAA3+DAA3+ADA3+DDA3+

AAD3+DAD3+ADD3+DDD3

(8)

因此，由WPT基本算法可知其具有更为精确的局部分析能力，可对低频和高频部分均作细分，为信号去噪领域提供了一种相对于小波去噪更加灵活、精细的方法。

1.3 基于VMD-WPT的信噪分离方法

在反应堆中，由于冷却剂连续流动冲刷压力容器等会产生一个持续的本底加速度信号，如果发生撞击事件，在本底信号的基础上将会叠加一个振荡衰减的冲击信号[3]，且本底信号和冲击信号均为宽频带信号，模拟的本底信号与叠加信号如图2所示。此外，背景噪声的来源还有来自于主泵的转动和管道的振动等，进一步加大了冲击信号的辨识难度。

本文提出一种基于VMD-WPT的反应堆松动部件冲击信号的信噪分离和特征提取方法，该方法实质上是一种从粗到细的二次滤波过程。之所以将2种方法相结合，是考虑到松动部件冲击信号是一种振荡衰减信号，噪声信号是一种非高斯噪声，且冲击信号和噪声信号均为宽频带信号。在低信噪比的情况下，WPT方法在频域上几乎得不到冲击信号的频率特征，当冲击信号完全被噪声淹没时，WPT方法将会失效[5]。而VMD方法能将信号分解为一系列具有中心频率和有限带宽的模态分量，选取冲击分量较大的模态重构信号即可滤除部分噪声，在此基础上再发挥WPT频率分辨率高的优点，即可有效提高冲击信号的信噪比。

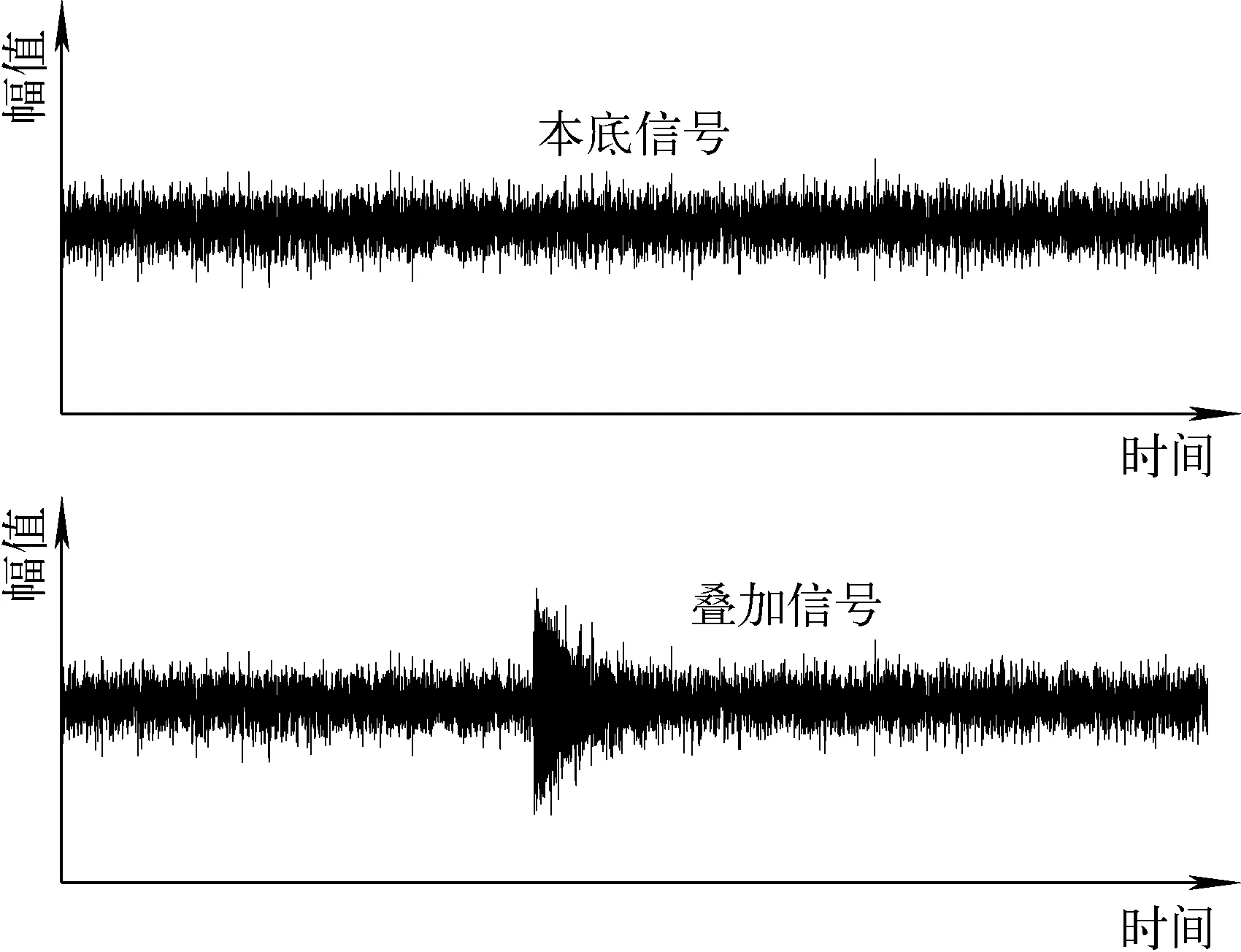
图2 噪声本底信号与叠加信号Fig.2 Background noise signal and superimposed signal

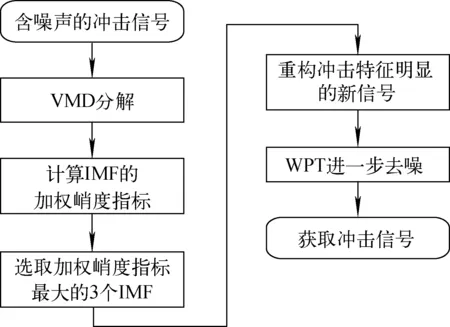
图3 基于VMD-WPT的信噪分离过程Fig.3 Signal-noise separation process based on VMD-WPT

算法流程图如图3所示，通过仿真模拟和冲击实验的方式获取原始信号，利用VMD算法将原始信号分解为一系列具有中心频率和有限带宽的模态分量。由于VMD的分解性能对模态数K的取值非常敏感，如果K取值过大，信号会过分解出现频率混叠的现象；如果K取值过小，将很难获得有用的特征分量。因此本文根据相关系数确定VMD分解的模态数K，计算各IMF之间的相关系数并获取其中的最大值，使最大相关系数不大于阈值0.1[10]。这些获取的IMF中有的主要包含冲击分量，有的主要包含噪声分量，因此根据冲击信号与噪声信号统计特性的不同，建立有效的评价指标，并作为依据选取冲击分量较多的IMF重构信号。加权峭度指标结合了峭度和相关系数2个指标的优点，能较大程度上降低有效冲击信号的遗漏。因此在VMD分解之后计算各IMF的加权峭度指标，为防止过度去除有用信号，保守选取加权峭度指标最大的3个IMF重构一个具有明显冲击特征的新信号，这个过程相当于一个滤波器组对原始信号进行初步的去噪。由于噪声是一种宽频带的有色噪声，所以重构的新信号还含有一定的噪声分量。最后，考虑到WPT具有良好的时频局部化优点，因此采用WPT对重构的新信号作进一步的去噪处理，从而提取信号的冲击特征。

2 仿真验证

建立简化的反应堆压力容器及内部构件的有限元模型，主要包括压力容器、吊篮组件和控制棒导向筒组件，模拟松动部件跟随冷却剂进入压力容器撞击吊篮以及冲击信号被压力容器上封头的加速度传感器捕获的过程，模型如图4所示。依次对模型进行模态分析、流场数值计算和瞬态动力学计算[11]，获得带有流致振动信号的松动部件冲击信号，计算时间为1 s，步长为0.001 s。为验证本文提出方法的去噪效果，在原始信号的基础上加入噪声使信噪比SNR=-5 db，原始信号与噪声信号经标准化处理后如图5所示。

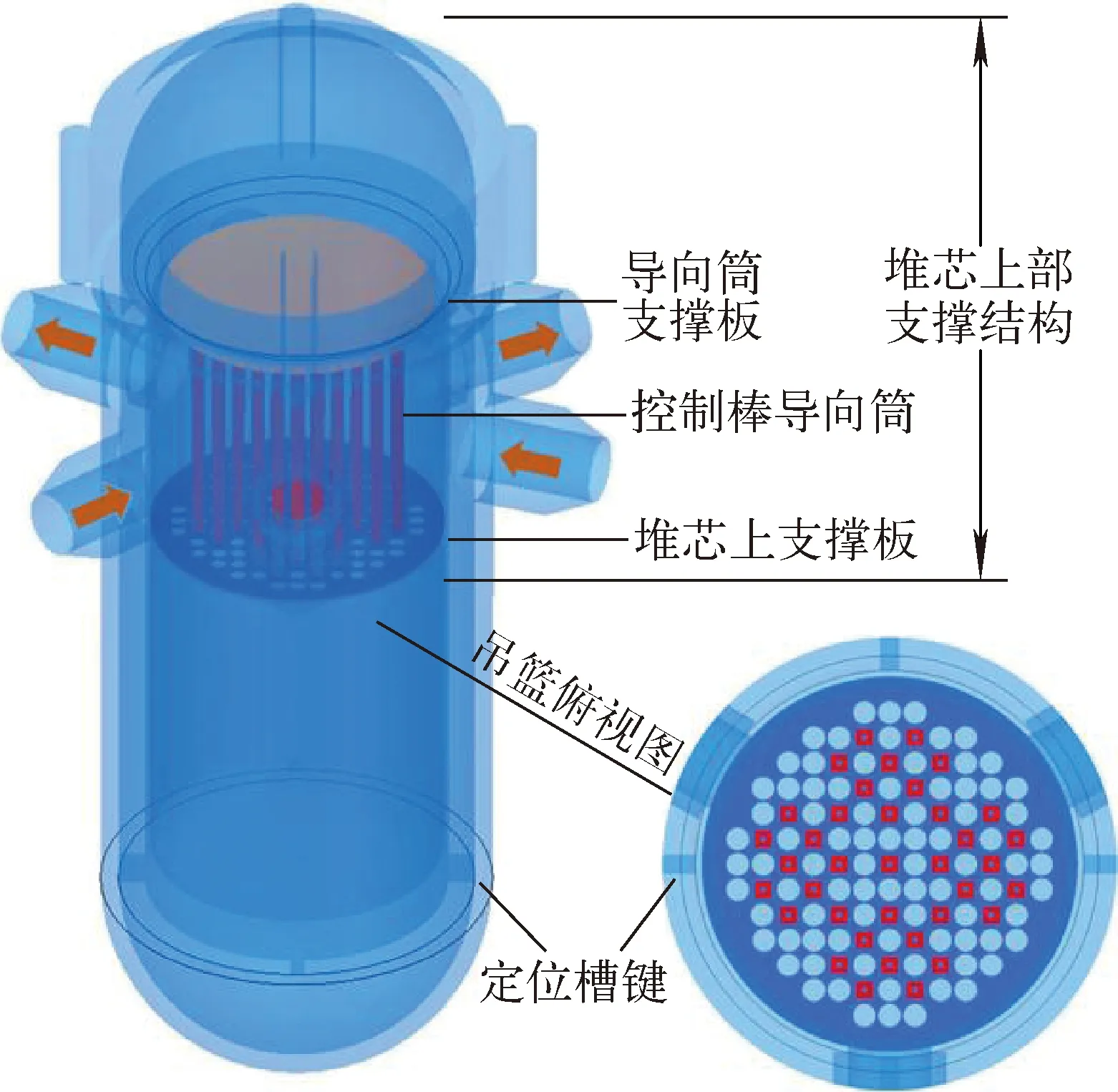
图4 反应堆有限元模型Fig.4 Finite element model of reactor

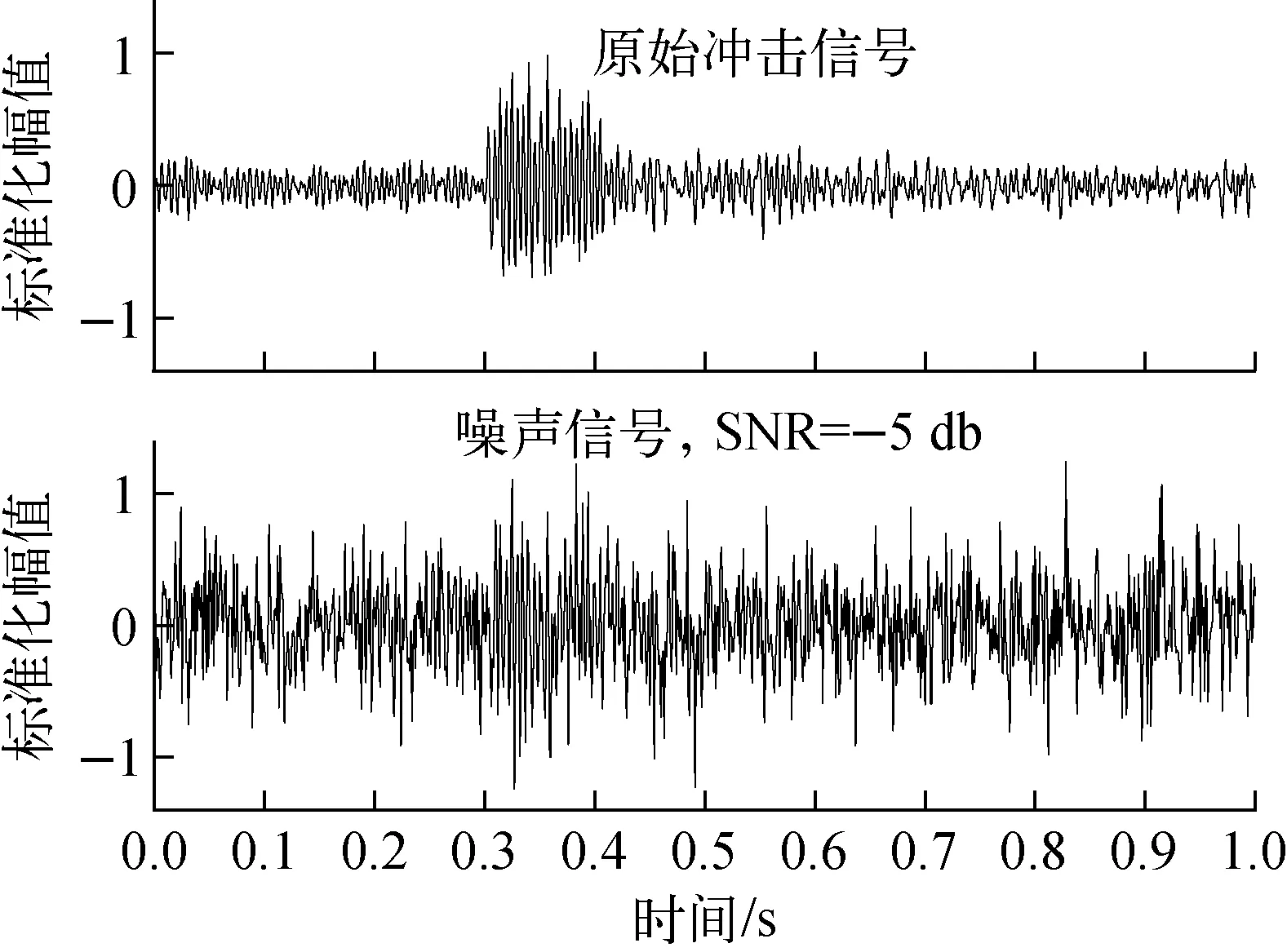
图5 松动部件原始冲击信号与噪声信号Fig.5 Original impact signal and impact signal with noise of loose part

图6 各IMFs与相应的加权峭度指标Fig.6 IMFs and corresponding weighted kurtosis index

采用VMD算法对噪声信号进行分解，根据各IMF间最大相关系数准则，确定分解模态数K=6，然后计算各IMF的加权峭度指标，如图6所示。加权峭度指标最大的3个IMF分别为IMF3、IMF4、IMF2，说明这3个IMF含有较多的冲击成分，因此选取这3个IMF重构新信号。然后采用WPT对新信号进一步去噪，采用“db4”小波基函数将信号分解为4层，并用软阈值函数对小波包系数进行处理，IMF重构信号和WPT去噪后的信号如图7所示。从图7可看出，IMF重构信号的信噪比SNR=1.556 db，相比原始噪声信号得到了很大的提升，且能看到明显的冲击成分。经WPT再次去噪后，信号的信噪比(SNR=3.902 db)进一步升高，冲击成分更加明显。因此，本文提出的方法能在强背景噪声下有效提取出反应堆松动部件的冲击响应信号，提高信号的信噪比。

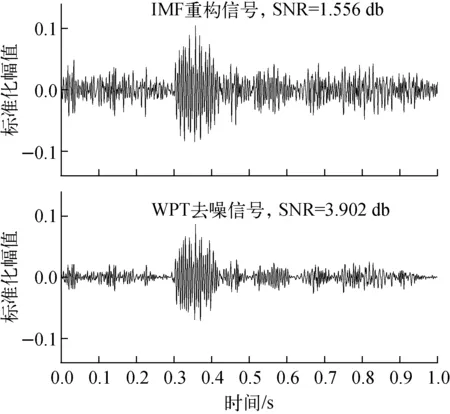
图7 IMF重构信号与WPT去噪信号Fig.7 Signal reconstructed by IMF and signal denoised by WPT

3 实验验证

由于实验室研究较难获取核电厂松动部件的冲击响应信号，因此科研人员常采用钢板作为一回路压力边界的模拟物，用钢球或螺母模拟松动部件撞击钢板产生冲击信号。根据这一思路，本文设计了图8所示的实验装置。采用不同质量的钢球掉落撞击钢板来模拟反应堆内松动部件对一回路压力边界的冲击过程，安装在钢板中心的压电式加速度传感器接收到钢球撞击产生的振动信号后，模拟电压信号经放大器放大后由数据采集卡转换为数字信号送入计算机。钢球初始高度为1 m；加速度传感器型号为CA-YD-181，量程为500g，灵敏度为10 mV/g；放大器的型号为YE5854A；数据采集卡的型号为USB04232M12。设置数据采集卡的采样频率为1 MHz，采样时间为0.5 s，对获取的数据进行二次采样，使其采样频率降为50 kHz。

图8 冲击实验原理图Fig.8 Schematic diagram of impact experiment

为验证本文方法在不同噪声水平下冲击信号的提取效果，对45 g钢球撞击产生的原始冲击信号添加不同信噪比(-5、-10、-15 db)的噪声，其冲击信号提取效果如图9所示。从图9可看出，获取的松动部件冲击信号为振荡衰减信号，与实际情况相符[3]。随着噪声水平的增加，原始冲击信号被完全淹没在噪声中，通过幅值无法检测出冲击事件。采用本文提出的方法分别对不同信噪比下的噪声信号进行去噪处理，均成功分离出了冲击特征信号，从而验证了该方法在不同噪声水平下的稳定性。

为验证本文方法在不同冲击强度下信号的提取效果，对不同质量m(60、100、195 g)钢球撞击产生的冲击信号分别添加噪声使信噪比SNR=-5 db，其冲击信号提取效果如图10所示。从图10可看出，随着钢球质量的增加，冲击的强度增大，因此信号的频域特征也会有所差异，这就要求算法具有一定的鲁棒性，对不同频域特征的冲击信号具有适应性。从结果可看出，本文方法成功地从不同冲击强度的噪声信号中分离出了冲击特征信号，从而验证了该方法在不同松动部件冲击强度下的稳定性。

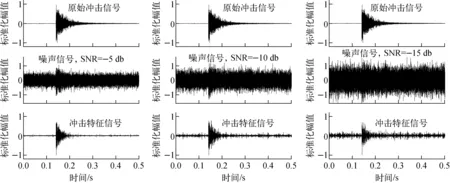
图9 不同信噪比下冲击信号的提取效果Fig.9 Performance of proposed method under different SNR

图10 不同质量钢球冲击信号的特征提取效果Fig.10 Extraction performance of impact signals produced by different balls

4 小结

针对反应堆强背景噪声下松动部件冲击信号提取困难的问题，本文提出了一种基于VMD和WPT相结合的信噪分离和特征提取方法，采用该方法分别对低信噪比下由仿真模拟和冲击实验获取的信号进行去噪处理，均成功分离出了冲击信号，有效提高了信号的信噪比，并在不同的噪声水平和冲击强度下，该算法具有较好的鲁棒性。在后续工作中，将继续对松动部件的质量估计和定位分析的方法展开进一步研究。