全方向无线电能传输电磁耦合系统仿真分析

谢文燕，陈 为

（福州大学电气工程与自动化学院，福州 350108）

无线电能传输 WPT（wireless power transfer）技术是基于电磁感应原理实现电能从空气介质距离传递的一种新型能量传输技术，其具有可靠性高、灵活性好、维护费用低以及环境亲和力强等优点，近年来发展迅速[1-6]。经过一个多世纪的发展和研究，该技术硕果累累，特别地，“贴板式”的无线充电器已实现产品化，广泛应用于智能手机和平板电脑等消费类电子产品领域。然而“贴板式”无线充电要求设备紧贴于充电板，极大地限制了便捷性和用户体验。对于一些小型便携电子设备（如蓝牙耳机）和智能可穿戴设备（如智能手表）等，放置的位置、方向一般都是任意的，当接收线圈与发射线圈之间发生平移或旋转时，接收线圈拾取到的能量是有限的，有时甚至不能正常工作。因此，对全方向WPT技术进行研究具有十分重要的意义。

早在2003年，德国德累斯顿大学的O’Brien发表了2篇与WPT方向性相关的文章[7-8]。文献[7]研究在三维空间中发射侧旋转磁场的设计；文献[8]通过采用3个正交线圈绕制的接收线圈结构，实现三维空间中任意旋转角度下电能的无线传输，但没有分析接收线圈在不同旋转角度下电能的传输能力。文献[9-10]采用2个电流幅值可控的独立电源，控制两正交圆环形线圈产生在二维空间内的旋转磁场；文献[11]采用相位差为90°的电源驱动两正交圆环形线圈产生0°～360°全向周期旋转磁场。然而这些研究局限于在二维空间内产生全向磁场，为进一步提高空间磁场自由度，使能量传向空间任意方向，文献[12]提出三维正交圆环形线圈结构，实现三维空间内任意位置传输功率，但其只在结构的中心位置产生均匀分布磁场，没有实现真正意义上的全方向WPT，极大地限制了其应用场合。此外，上述对多线圈正交型的发射线圈结构都需要对2个或3个的激励进行控制，结构复杂且控制难度比较大，存在充电死区。天津大学研究人员针对单一接收平面圆环形线圈的三维正交圆环形发射线圈结构存在充电死区的问题，对接收线圈结构进行优化设计，在原始单一接收平面圆环形线圈结构的基础上，在中间部位加入十字交叉型磁心并绕上2个绕组构成三绕组接收线圈结构，同时对中间十字交叉磁心结构的长度和宽度进行优化设计，旨在提高系统在特殊位置的传输功率和传输效率[13]，但这增加了接收线圈的重量和磁心损耗。针对植入式医疗电子设备的运用场合，清华大学提出一种新型微球内窥镜系统WPT方案[14]，在解决方案中，考虑到微球体积小且进入图像阅读器后姿态的不确定性，不能采用多个接收线圈，在图像阅读器上采用由5个线圈绕制而成的立体磁场发射器，提出了一种可根据图像阅读器内微球的位置，选择功率传输效率最高的线圈发射功率的自适应控制机制，但没有对所提电磁耦合结构进行理论分析，也没有讨论微球位置变化对系统性能的影响。

基于上述情况，本文对多发射线圈的全方向WPT电磁耦合结构进行理论和仿真分析，所研究的全方向多发射线圈结构的每个发射线圈处于分时工作状态，通过实时判断接收线圈的位置，自适应地选通与接收线圈耦合最好的发射线圈工作，从而获得最大的输出功率。该控制方法简单，易于实现。

1 全方向WPT电磁耦合线圈结构与系统控制策略分析

1.1 电磁耦合线圈结构分析

全方向WPT是指在有效的电能传输区域范围内，传输的能量受距离和方向的影响较小，设备在任意位置都能进行有效供电。因单一发射线圈不易形成全方向性磁场，故本文采用多个发射线圈构成磁场发射装置。图1（a）给出了一种常见的全方向磁耦合系统线圈结构，发射线圈呈三维正交分布。

图1 基本电磁耦合系统Fig.1 Basic electromagnetic coupling system

除发射线圈和接收线圈外，通常电磁耦合系统还包括补偿网络。典型的补偿网络结构有串联-串联补偿、串联-并联补偿、并联-串联补偿和并联-并联补偿4种[15]。由于串联-串联补偿的补偿电容大小与负载和互感均无关，更易于实现阻抗匹配，故本文所分析的电磁耦合系统补偿网络采用串联-串联补偿。此外，由于本文研究的全方向多发射线圈结构的每个发射线圈处于分时工作状态，则实际系统在工作时的任意时刻可等效为两线圈结构分析，其等效电路模型如图1（b）所示。图中Uin为输入电压，Ipi、Lpi、Rpi和 Cpi分别为第 i个发射线圈的电流、自感、内阻和补偿电容，Is、Ls、Rs和 Cs分别为接收线圈的电流、自感、内阻和补偿电容，Mi为第i个发射线圈与接收线圈的互感，Ro为负载电阻，Io为流过负载电阻的电流。

图1（b）中，由电磁感应定律可建立方程组为

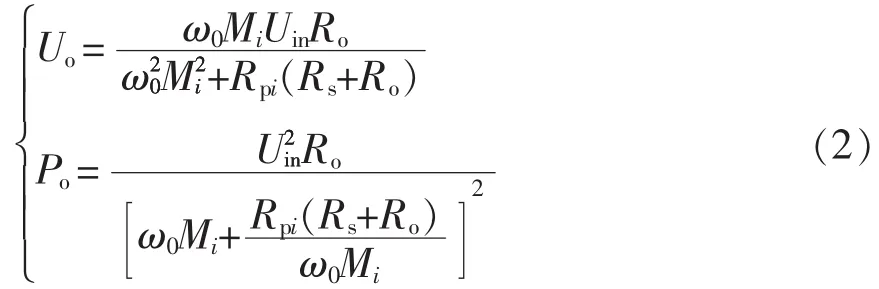
根据式（2）可知，系统的输出电压和输出功率与输入电压 Uin、互感 Mi、线圈内阻 Rpi和 Rs以及系统的工作角频率ω0有关，且与互感Mi不是线性关系。

从而，Po与Mi的关系见图2，图中Mmax表示发射线圈和接收线圈完全耦合时（耦合系数为1）的互感最大值，此时系统输出功率Po_Mmax为

假设系统所需的最小输出功率为P1，根据式（4），合理设计 ω0、Lpi、Ls、Uin、Rpi和 Rs的值，可以使Po_Mmax＞P1。所以，当 Mi满足 M0＜Mi＜Mmax时，存在 Po＞Po_Mmax＞P1，系统的输出功率满足最小输出功率要求，因此，只需考虑 Mi＜M0的情况。由于 Mi＜M0时，Po随Mi增大而增大，在此区间内可认为Mi越大，Po越大。虽然，互感 Mi在 M0＜Mi＜Mmax的区间，不满足 Mi越大，Po越大，但此时输出功率已满足最低功率要求。例如：在图2中，b点的互感比a点大，但对应的输出功率比a点小，虽然这并不满足“Mi越大，Po越大”，但此时b点的功率已满足系统最低功率P1的要求。因此，在多发射线圈的全方向电磁耦合结构中，可通过合理的参数设计，选通互感最大的那个发射线圈工作，使输出功率满足系统需求，提高发射线圈磁场利用率，同时还可达到减小磁场辐射的目的。反过来，为保证接收线圈在有效电能传输区域的任意位置下，系统输出功率均能满足最小功率需求，在设计多发射线圈的全方向电磁耦合系统时，必须考虑接收线圈在全方向最小互感下的输出功率能够满足系统的最低功率需求。

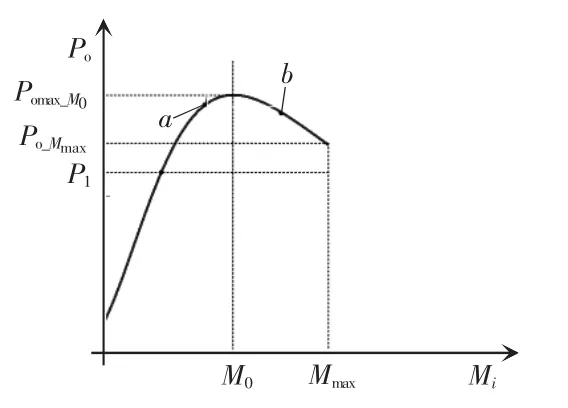
图2 输出功率与互感的关系曲线Fig.2 Curve of relationship between output power and mutual inductance

上述分析是在电压源激励下进行的，当采用电流源激励时，也假设，则系统的输出电压和输出功率分别为

由式（5）可知，当采用电流源激励时，Uo和Po的大小均随Mi的增大而增大，因此，可通过判断互感的大小来有效判断输出功率的大小。

1.2 电磁耦合系统控制策略

第1.1节分析了发射线圈和接收线圈的互感与输出功率的关系，但系统在实际工作中，多发射线圈结构每个线圈与接收线圈的互感是无法实时测量的。那么如何通过系统参数的监测，判断哪个线圈耦合最好呢？为简化控制和减少磁场泄露，本文所讨论的控制方案多个发射线圈每时只有一个线圈工作，由式（1）和可得发射线圈电流为

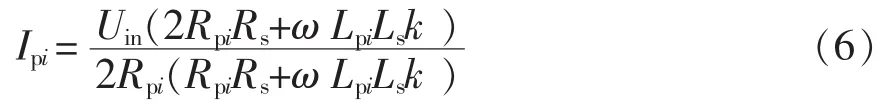
根据式（6）可绘制出各发射线圈电流Ipi与耦合系数ki的关系曲线，如图3所示。从图3可知，Ipi随ki的增大而减小，因此在实际工作中，可以通过监测Ipi的大小来判断ki的大小，Ipi越小说明ki越大。

图3 发射线圈电流与耦合系数的关系曲线Fig.3 Curve of relationship between transmitter current and coupling coefficient

根据上述分析，本文提出的控制方案首先给定输入电压，轮流导通各个发射线圈，分别监测此时各个发射线圈的电流，得到 Ip1，Ip2，Ip3，…，Ipn；然后比较 Ip1，Ip2，Ip3，…，Ipn的大小，选通具有最小电流值的发射线圈。图4给出了一种实际电路和控制流程，为使系统具有通用性，假设发射线圈结构含有n个发射线圈。

综上所述，在多发射线圈的全方向电磁耦合结构中，无论是采用电压源激励还是电流源激励，在系统参数设计合理的情况下，均可认为互感大的发射线圈工作时可以满足系统的输出功率要求，实际电路通过监测发射线圈电流的大小选通此发射线圈工作。那么在多发射线圈的全方向电磁耦合结构中如何根据接收线圈的位置设计发射线圈或是如何确定在全方向下系统的最小互感？后文将采用数值计算的方法对常见的全方向电磁耦合结构进行分析并通过电磁仿真进行验证，该方法可用于指导发射线圈结构的设计。

图4 发射侧电路与控制流程Fig.4 Transmitting-side circuit and flow chart of control

2 全方向无线电能传输场景分析

图5给出了一种常见的全方向磁耦合系统线圈结构，发射线圈呈三维正交分布。

图5中，虚线球体P代表发射线圈结构，外围实线球体Q表示有效的电能传输区域。由于结构具有对称性，为简化分析，将有效电能传输区域分成8个大小完全相同的1/8球体，假设有效充电区域内任意点的坐标为（x，y，z），则 8 个有效电能传输区域可分别表示为（x＞0，y＞0，z＞0）、（x＞0，y＞0，z＜0）、（x＞0，y＜0，z＞0）、（x＞0，y＜0，z＜0）、（x＜0，y＞0，z＞0）、（x＜0，y＞0，z＜0）、（x＜0，y＜0，z＞0）和（x＜0，y＜0，z＜0）。根据对称性，只需对其中一个1/8球体区域进行分析。

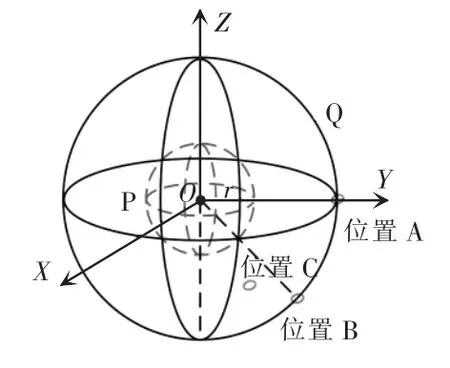
图5 三维正交磁耦合系统线圈结构Fig.5 Coil structure of 3D orthogonal magnetic coupling system

以坐标为（x＞0，y＞0，z＜0）的 1/8 球体区域为例，由于发射线圈与接收线圈的互感与距离成反比，互感又是影响传输功率和传输效率的关键因素，接收线圈位于1/8球体表面时，与发射线圈相距最远，此时互感最小，因此1/8球体表面可视为互感最小区域。此外，当接收线圈发生平移或旋转时，互感会发生变化，从理论上直接计算分析全方向任意点互感相对不易。

为简化分析，假设发射线圈与接收线圈（这里只考虑单个接收线圈）中心点之间的距离为L，即有效电能传输区域是半径为L的球体，同时选取该1/8球体区域表面的 3个典型坐标位置：，如图5所示。由于这3个位置均位于有效电能传输区域的表面且在1/8球体表面位置分散，因此可近似认为在这3个典型位置下，接收线圈方向变化时其与发射线圈的最小互感即为全方向最小互感。

为模拟接收线圈不同方向时的场景，通过分析，考虑以下4种场景：场景1，接收线圈平行于xoy平面并绕z轴旋转；场景2，接收线圈垂直于xoy平面，平行于yoz平面，并绕z轴旋转；场景3，在场景1的基础上接收线圈绕y轴旋转45°，使之与xoy平面和yoz平面均呈45°，并绕z轴旋转；场景4，在场景1的基础上接收线圈绕x轴旋转45°，再绕y轴旋转45°，并绕z轴旋转。通过对上述 3个典型位置A、B和C下4种场景的分析，大致模拟全方向的效果。图6为4种场景下接收线圈旋转处理示意，此处旋转变换是以接收线圈所在坐标系为参考坐标系。

图6 4种场景下接收线圈旋转示意Fig.6 Schematic of receiving coil rotation in four scenarios

上述分析是基于常见三维正交圆环形线圈结构，但这种方案中接收线圈与发射线圈中心的距离比接收线圈与发射器球体表面的距离多了一个半径r，导致有效传输距离大打折扣。图7（a）给出了三维正交圆环形线圈结构传输距离示意。此外，当接收线圈垂直于2个发射线圈时，接收线圈在空间的某一位置存在充电死区，接收到的功率很小。

为此，本文在三维正交圆环形线圈方案的基础上提出正方体方案，将发射线圈布置在正方体的6个面，当线圈工作时，接收线圈与发射器的实际距离将等于接收线圈与发射器本体的表面距离而不是中心距离，即传输距离从r+d减小为d，使系统在大部分位置具有更大的互感（由于正方体6个线圈之间并非完全正交，导致在局部位置发射线圈均与接收线圈呈正交或近似正交状态，局部位置的互感会更小，此现象后文会证明）。正方体结构方案如图7（b）所示，系统实际工作时6个线圈处于分时工作状态，通过实时判断接收线圈的位置，自适应选通与接收线圈耦合最好的发射线圈工作，从而获得最大的输出功率。为直观分析实际工作时哪个线圈的耦合最好，选择哪个线圈工作，本文以便携式电子产品（如手机、蓝牙耳机、手表等）的应用场合为例，假设发射器外围尺寸为 7 cm×7 cm×7 cm且发射线圈采用圆环形线圈，半径为r，采用单一接收圆环形线圈，线圈半径为R，如图7（b）所示。同时分析上述3个典型位置A、B和C在4种场景下各个发射线圈与接收线圈之间的互感，以此模拟接收线圈在全方向下的工作情况（当应用场合是手表时，可采用矩形接收线圈置于表带中，本文不再赘述）。

图7 全方向磁耦合结构方案Fig.7 Omnidirectional magnetic coupling structure scheme

3 磁耦合线圈结构方案数值建模与分析

3.1 磁耦合结构数学模型的建立

如图7（a）示，三维正交圆环形发射器中心位于坐标原点 O1（0，0，0），发射线圈半径为 r，则其参数方程可表示为

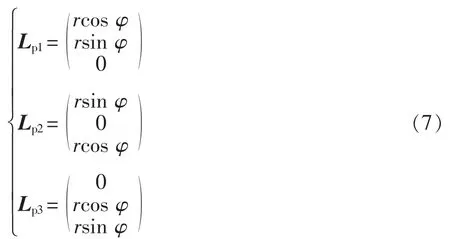
如图7（b）示，正方体发射器中心位于坐标原点 O1（0，0，0），正方体边长为 a，发射线圈半径为 r，则6个发射线圈的参数方程可表示为

考虑到接收线圈位置的任意性，可能发生平移或旋转，接收线圈参数方程可表示为

式中：γ表示绕z轴旋转角度；β表示绕y轴旋转角度；α 表示绕 x 轴旋转角度；（x0，y0，z0）表示发生平移的距离。根据聂依曼公式，可以得到发射线圈Lp1、Lp2、Lp3、Lp4、Lp5、Lp6与接收线圈 Ls之间的互感为

式中：n1和n2分别表示发射线圈和接收线圈的匝数；i=1，2，3，4，5，6。

3.2 磁耦合结构数学模型电磁仿真验证

为验证第3.1节建立模型的准确性，以n1=n2=1，L=10 cm，r=3.5 cm，R=2.5 cm，接收线圈位于位置A时4种场景下的单位互感为例，采用Mathcad工程计算软件对所建立的磁耦合结构数学模型进行理论分析并用ANSYS MAXWELL电磁仿真软件进行验证。图8给出了当接收线圈在位置A时，即O2（0，10 cm，0），正交圆环形线圈结构和正方体线圈结构接收线圈在4种场景下，单位互感与接收线圈绕z轴旋转角度的变化关系。

由图8可以看出，两磁耦合结构在接收线圈绕z轴旋转变化时，单位互感的理论结果与仿真结果数值上有轻微的差距，这是由于在ANSYS MAXWELL仿真时，发射器各个发射线圈尺寸无法设置成完全一样大小所致，但其总体变化趋势是一致的，验证了第3.1节所建数学模型的正确性。因此，后文均采用理论分析方法对所述线圈结构进行分析。

3.3 两种磁耦合结构耦合特性分析

第3.2节中图8给出了当L=10 cm，r=3.5 cm，R=2.5 cm时，在位置A下4种场景单位互感与接收线圈绕z轴旋转角度的变化关系。考虑全方向的情况，图9给出位置B和C下的关系。

从图8和图9可知：

（1）两种线圈磁结构互感均与接收线圈的位置、充电场景和旋转角度有关，位置不同互感不同，充电场景不同互感不同。因此，系统实际工作时，为减小磁场辐射，提高磁场利用率可以采用选通耦合性能最好的那个线圈工作。

（2）当接收线圈的位置和旋转角度固定时，发射线圈与接收线圈之间的互感会随着充电场景的不同而不同，且不同场景下耦合性能最好的线圈不同。例如，采用正方体发射线圈结构方案，当接收线圈位于位置B，旋转角度为90°时，4个充电场景下的最大互感分别为1.9、1.9、1.2和1.0 nH，在场景1下线圈5与发射线圈耦合最好；在场景2下则是线圈1耦合最好；在场景3下线圈1和5与发射线圈的耦合相同且最好。

（3）当接收线圈的旋转角度和场景固定时，接收线圈的位置改变，互感会发生变化。例如，采用正方体线圈方案，在场景1下，当接收线圈的旋转角度为45°，接收线圈位于位置A时，线圈1和4与接收线圈的耦合最好，互感为0.41 nH；位于位置B时，线圈5与发射线圈的耦合最好，互感为1.90 nH；位于位置C时，则是线圈1与发射线圈的耦合最好，互感为1.02 nH。

（4）通过对图8和图9的3种位置、4种场景的分析，可以得到对应的各最小单位互感和全方向最小单位互感，如表1所示。（这里的最小单位互感是指所选通的发射线圈与接收线圈在旋转角为0°～180°变化区间的最小互感，该值可用于指导设计电磁耦合系统的其他参数。）

结合图8、图9以及表1的数据可得，在发射体的外围最大尺寸相同（7 cm×7 cm×7 cm）且正方体方案发射线圈与接收线圈的等效传输距离变小的情况下，正方体线圈方案各位置不同场景下的互感，大部分的单位互感比正交圆环形线圈方案的大，但在局部位置小的互感反而减小了，因而在全方向下的最小单位互感（0.34 nH）较正交圆环形线圈方案的（0.48 nH）小。例如，在位置A场景1下，由于发射线圈2、3、5、6均与接收线圈正交，而发射线圈1、4与接收线圈的距离较远，导致其互感较正交圆环形线圈方案小；又如，在位置A场景3下，接收线圈绕y轴旋转45°，导致与发射线圈1、2、4、5的互感大大降低，若接收线圈绕z轴的旋转角为0°或180°，发射线圈3、6与接收线圈近似正交，导致此时系统的互感更小。此现象证明了第2节理论分析的正确性。

表1 两种线圈结构方案单位互感Tab.1 Unit mutual inductance in two coil structure schemes

图8 两种线圈结构方案在位置A下4种场景的单位互感Fig.8 Unit mutual inductance at position A of two coil structure schemes in four scenarios

图9 两种线圈结构方案在位置B和C下4种场景的单位互感Fig.9 Unit mutual inductance at positions B and C of two coil structure schemes in four scenarios

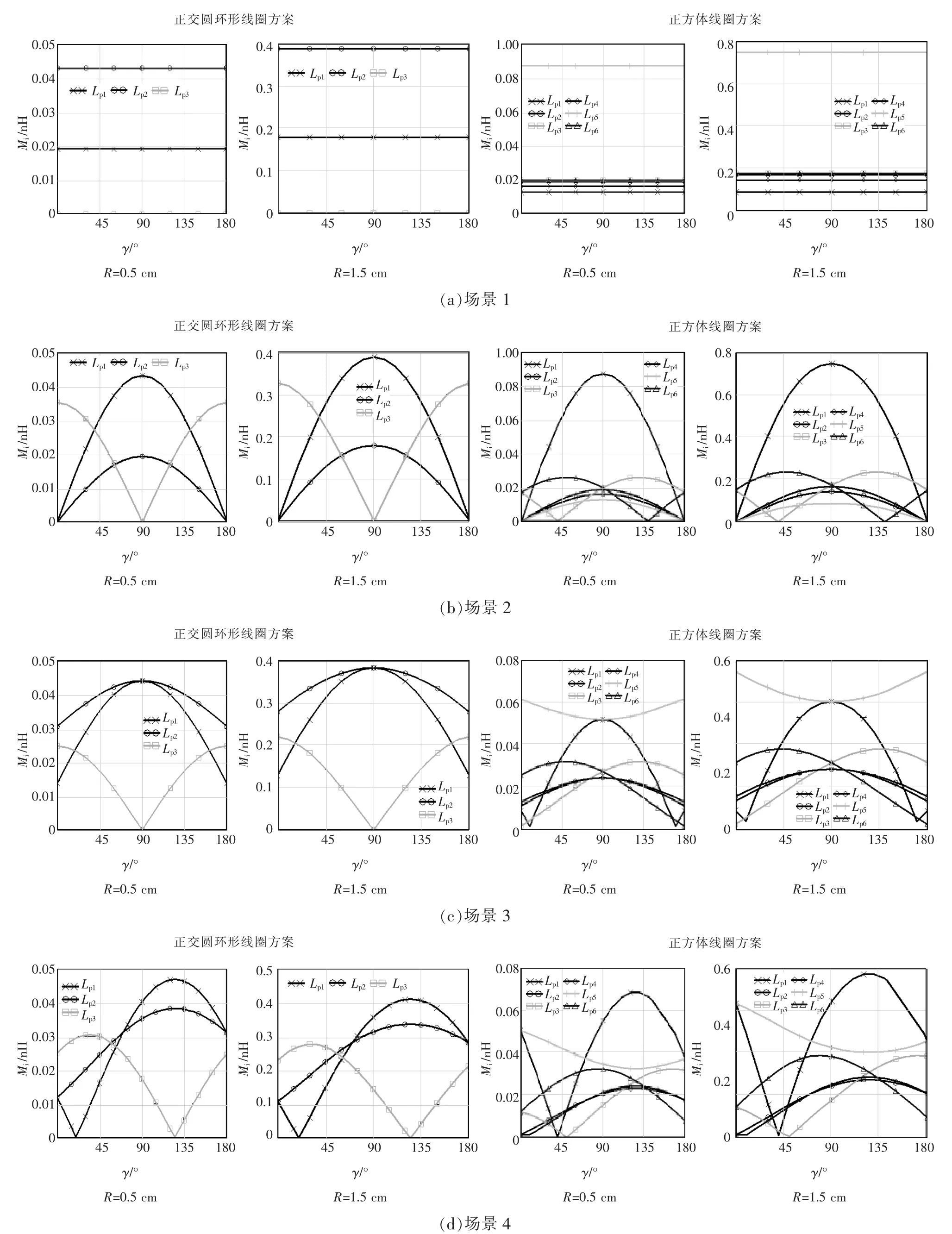
图10 不同接收线圈大小时两种磁结构方案在位置B下的单位互感Fig.10 Unit mutual inductance at position B of two magnetic structure schemes with different receiver coil sizes

图11 不同发射接收距离时两种磁结构方案在位置C下的单位互感Fig.11 Unit mutual inductance at position C of two magnetic structure schemes at different transmitting and receiving distances

为了进一步比较两种磁耦合结构的耦合特性，图10给出了不同接收线圈大小时，两种磁结构方案在位置B下4种场景的单位互感与旋转角度的关系，图中，R为接收线圈半径大小，单位为cm，L=10 cm，r=3.5 cm，实际传输距离为L-R-r。图11给出了不同发射接收距离时，两种磁结构方案在位置C下4种场景的单位互感与旋转角度的关系。图中，L为发射器中心与接收线圈中心点的距离，单位为cm，R=2.5 cm，r=3.5 cm，实际传输距离为L-R-r。

从图9和图10可以看出，两种磁结构方案的单位互感随着接收线圈尺寸的增大而增大，同时在位置B下除场景2的局部旋转角度区域外，正方体线圈结构的单位互感均大于三维正交圆环形线圈结构。从图9和图11可以看出，两种磁结构方案的单位互感随着发射接收距离的增大而减小，同时在位置C下4种场景的正方体线圈结构的单位互感均大于三维正交圆环形线圈结构。

4 结论

（1）运用电路理论，建立了全方向无线电能传输电磁耦合系统的数学模型，推导输出电压和输出功率的表达式，得出输出功率与互感的关系。

（2）给出了一种全方向无线电能传输磁场控制方案：通过监测发射线圈电流的大小，选通具有最小发射线圈电流的线圈。

（3）对全方向无线电能传输的充电场景进行分析，并对三维正交圆环形线圈和正方体线圈方案的传输距离进行了分析对比。

（4）建立了正交圆环形线圈结构和正方体线圈结构方案互感的数学模型，采用ANSYS MAXWELL电磁仿真软件验证所建互感数学模型的正确性，并据此模型分析互感与接收线圈的位置、充电场景和旋转角度的关系。

（5）本文对电磁耦合系统的分析方法对移动式便携设备如手机、手表和蓝牙耳机等全方向无线充电电磁耦合系统的设计和控制具有一定的指导意义，但具体发射线圈结构的优化和控制细节问题有待进一步研究。