航空发动机矢量推力测量系统的静态校准及不确定度评定方法研究

吴 锋， 杨 桥， 张 有， 徐倩楠， 冯旭栋

(1.中国航发四川燃气涡轮研究院 高空模拟技术重点实验室，四川 绵阳 621000； 2.西北工业大学 动力与能源学院，陕西 西安 710129)

动力系统的矢量推力是新一代战机关键技战术指标，是新一代航空发动机发展的关键技术[1-3]。发展矢量推力技术，就必须开展相关配套试验研究，而实现对矢量推力的精确测量和评估，必须通过多分量推力测量系统(台架)实现[4]。

与常规的风洞六分力天平相比，航空发动机多分量推力测量系统的研制具有一定的独特性。首先，与风洞试验模型相比，航空发动机体积和重量更大，最大长度可达10 m；其次，发动机的安装结构更加复杂，一般有两个主支点和多个辅助支点，推力台架承受的推力和力矩范围也更大；再次，发动机排气温度很高，对推力测量系统的热防护也提出了更高的要求。因此，风洞试验中所采用的各种结构形式的天平往往难以满足航空发动机试验所需的矢量推力测量要求[5-8]。基于多个测力组件按照一定正交性和相关性布局的分布式推力测量系统是专门针对航空发动机矢量推力测量而发展的，目前国内外诸多著名发动机试验机构，如美国航空航天局(NASA)[9-10]、阿诺德工程研究中心(AEDC)[11]、美国海军军用实验室(NOTS)[12]等，均采用这种基于多测力组件的分布式推力测量系统进行发动机矢量推力的测量。

精度高、可靠性好的航空发动机矢量推力测量系统的研制与应用，不仅要求有很高的加工精度、严格的加工工艺，而且需要高精度的校准。航空发动机矢量推力台架的校准工作是试验台建设的最终关键步骤，它直接决定矢量推力测量系统最终能否满足发动机的测试需求[13]。由于多分量推力测量系统的精度要求很高，至今仍没有形成统一的标准或规范来评价其精度。目前，对多分量推力测量系统的性能评定主要包括两种方法：① 用系统校准时所施加的实际载荷与静态解耦得到的台架校准公式计算值之间的偏离程度来表征测量系统的精度，以校准残余误差标准差或最大值乘以适当的置信因子作为系统各个分量的不确定度[14-17]；② 进行额外的验证加载实验，用验证加载实验的实际载荷与台架校准公式计算值之间的偏离程度来表征系统精度[18-21]。以上两种方法都只能给出关于测量精度的一个恒定值，而推力台架的测量不确定度是随加载条件变化的，采用恒定的精度难以准确描述所有加载条件下的测量精度[22-23]。因此，如何准确地评定多分量推力测量系统面向具体任务的测量不确定度，成为在其应用中必须解决的一大难题。

本文主要针对分布式多分量推力测量系统的静态校准方法和面向测量任务的不确定度评定方法展开研究。基于试制的航空发动机多分量推力测量台架，建立了测量系统静态校准的数学模型，推导了校准系数的求解公式；在此基础上提出了一种基于校准系数误差传递的不确定度评定方法，采用该方法可以针对具体测量任务，得到台架在不同工作条件下的测量结果不确定度。

1 实验系统

1.1 矢量推力测量系统的结构及测量原理

本研究在一套试制的航空发动机多分量推力测量系统上开展。该系统主要由动架、定架和测力组件3个部分组成，结构如图1所示。系统共包含6个工作测力组件，用以限制发动机的6个自由度并测量发动机向台架施加的矢量推力。其中，测力组件R1、R2安装在主推力方向，R3、R4安装在侧向力方向，R5、R6安装在垂向力方向，各测力组件通过万向挠性件连接在动架与定架之间。

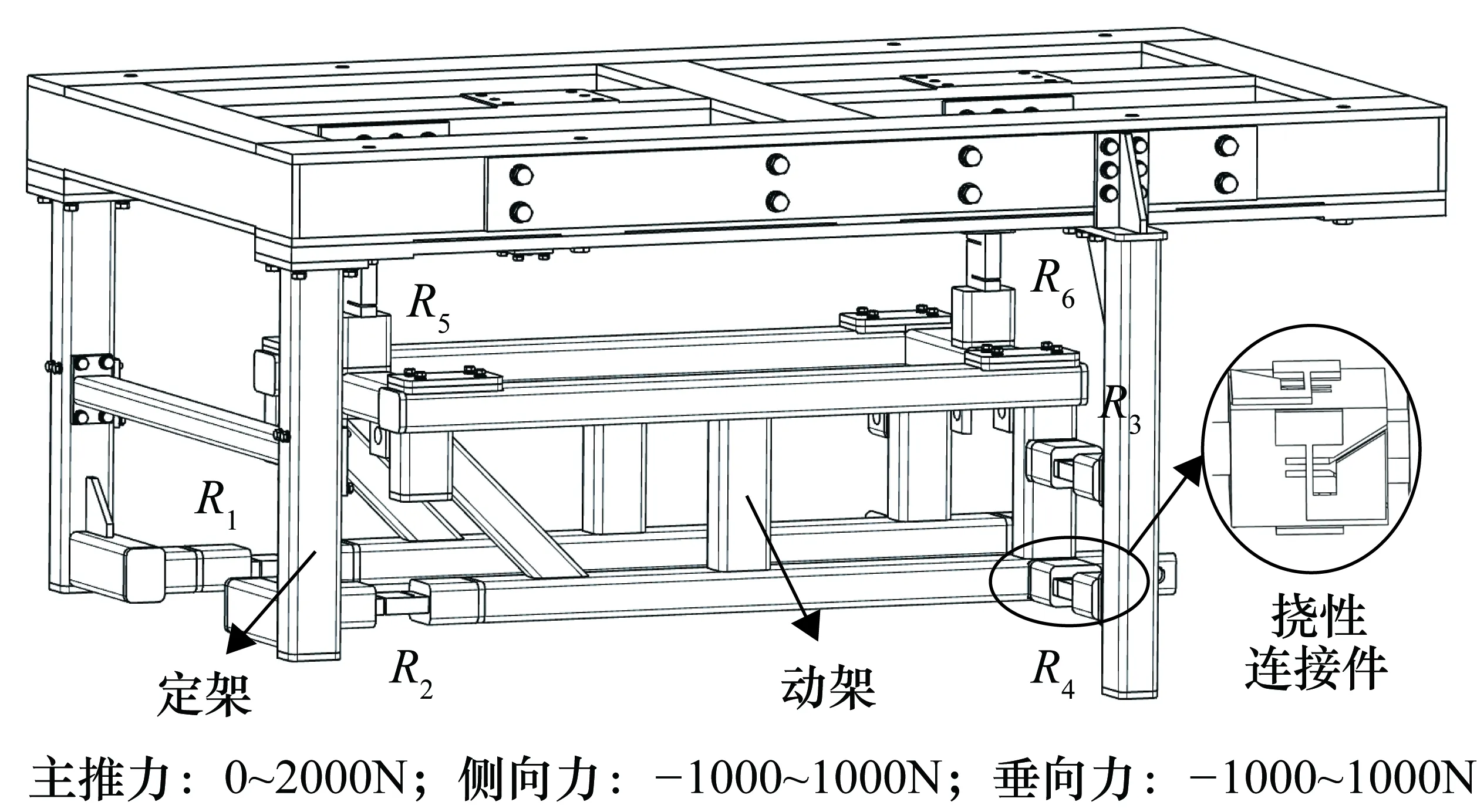
图1 矢量推力测量系统的示意图

发动机产生的矢量推力通过动架传递到各测力组件，测力组件将感受的轴向力转化为电压信号，通过VXI总线系统进入采集计算机，进而可以根据施加推力与测量信号的映射关系计算得到台架受到的力和力矩，从而实现发动机矢量推力的测量。

1.2 校准加载系统

为了准确模拟发动机产生的矢量推力，本文设计了一套砝码加载装置。该校准装置主要由加载架、校准力源(砝码、滑轮、连索)和单维校准力传感器组成，可用加载位置6个，分别对应于各工作测力组件。考虑到滑轮轴承的静摩擦力大小和方向是不确定的，对于加载精度的影响难以通过技术手段修正消除，为了避免由此引起的校准加载力误差，在加载点与砝码之间串联标准单维力传感器，以各单维力传感器的实测数据作为施加给台架的真实校准载荷。矢量推力测量台架及其校准加载系统实物如图2所示。

2 静态校准方法

发动机作用到台架上的矢量力与推力测量系统各个测力组件输出之间的映射关系必须通过静态校准来确定。静态校准的原理是通过校准设备向台架施加已知的标准校准载荷，由台架中各测力部件的输出值得到台架的测量力，从而计算测量力与校准力之间的相互对应关系。

图2 矢量推力测量台架及其校准加载系统实物

校准模型是用来描述作用在台架上的载荷值与多分量推力测量系统输出值之间的关系式。根据校准公式中自变量项的阶次，可以将校准模型分为一阶模型、二阶模型和高阶模型。文献[13]表明，二阶次以内的校准模型通常就可以满足对多分量推力测量系统的描述，并达到较高精度。

若用[Fc]6×1表示一个实验加载点的校准载荷，那么K个加载点的载荷数据可以构成一个6×K的校准载荷矩阵[Fc]6×K。类似地，K个加载点数据可以构造一个m×K的自变量矩阵[Rc]m×K，对于一阶模型，m=6；对于二阶模型，m=27。

那么，校准模型公式可以用矩阵形式表示为

[Fc]6×K=[A]6×m[Rc]m×K+[E]6×K

(1)

式中，[Fc]6×K为向台架施加的标准校准载荷构成的矩阵，任一实验加载点的校准载荷[Fc]6×1可表示为

[Fc]6×1=[F1,F2,F3,F4,F5,F6]T

(2)

[Rc]m×K为由多分量测量系统各测力组件输出结果构成的自变量矩阵，对于一阶模型，包含6项自变量，可表示为

[Rc]6×1=[R1,R2,R3,R4,R5,R6]T

(3)

对于二阶模型，包含27项自变量，可表示为

(4)

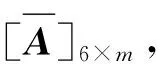
[Fc]6×K=[A]6×m[Rc]m×K

(5)

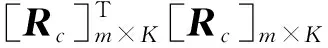
(6)

值得注意的是，当采用二阶校准模型时，由于自变量数量很多，在这些自变量中，有些自变量对结果的影响并不重要，有些自变量和其他自变量有很大程度的重叠，有些自变量数据的质量可能已经很差。为了避免由此引起的校准系数误差，同时也为了减小计算量，本文采用逐步回归分析方法对自变量项进行了取舍。

逐步回归分析方法的基本思想是，在所考察的全部因素中，按对因变量作用的显著程度的大小，取最显著的变量，逐个引入回归方程，对因变量作用不显著的那些变量自始至终都未被引入。另一方面，已被引入回归方程的变量，再引入新变量后如发现其对因变量的作用变为不显著时，则随时从回归方程中剔除，直至没有新变量能引入方程，且引入方程的所有变量均不需剔除为止[24]。

3 不确定度分析

不确定度是合理表征测量值分散性、与测量结果相联系的参数[25]。目前，最为常见的方法是采用校准时或额外验证时的实际载荷与静态解耦得到的台架校准公式计算值之间的偏离程度，作为评价多分量推力测量系统精度的不确定度指标。其中，偏离程度用残余误差的最大值或标准偏差来表征。

如果用Fi,max表示i方向可施加的最大力(或力矩)，Fi(cal)表示校准时i方向实际施加的力(或力矩)，Fi(ver)表示验证时i方向实际施加的力(或力矩)，那么，i方向力(或力矩)的相对校准残余误差ei(cal)可表示为

(7)

类似地，i方向力(或力矩)的验证相对残余误差ei(ver)可表示为

(8)

由此得到校准残余误差的最大值和标准偏差，进而对测量结果的精度进行表征。

上述方法理论简单、可操作性强，但是在实际应用中却可能导致一些问题：① 该精度指标能否准确描述系统的真实精度水平，极其依赖于校准数据点或验证数据点的选取，如果校准数据点没有合理控制或者无法完全覆盖多分量测量系统的工作状态包线，那么该指标对于测量系统精度的表征效果将大打折扣；② 由于该精度指标是一个恒定值，因而在描述某些加载情况时可能偏保守，在描述另一些加载情况时偏激进，无法准确获取多分量推力测量系统在执行特定测量任务时的不确定度。

为此，本文研究了一种基于校准系数误差传递的方法来评定系统各分量的测量不确定度，有效避免了传统方法在多分量推力测量系统测量结果误差评价上的局限性。

3.1 不确定度模型

本文采用基于校准系数误差传递的不确定度评定方法，多分量推力测量系统任意分量校准公式的 “测量不确定度传播”输入-输出模型如图3所示。该模型的输入包括两个部分：

① 校准系数的估计值aj，校准系数的标准不确定度u(aj)，以及各校准系数之间的协方差u(aj,ak)；

② 工作测力组件输出的估计值Rj，工作测力组件输出的标准不确定度u(Rj)，以及各工作测力组件输出之间的协方差u(Rj,Rk)。

图3 推力测量系统的不确定度模型

应用测量不确定度传播律[22]，可得多分量推力测量系统i方向上的力(或力矩)分量Fi的标准不确定度为

(9)

根据选择的置信概率，扩展不确定度可通过标准不确定度乘以相应的置信因子得到，即

U(Fi)=kuc(Fi)

(10)

3.2 校准系数的不确定度

校准系数矩阵是根据静态校准数据求解得到的最小二乘估计量，要确定校准系数的不确定度，首先需要计算校准数据的不确定度。校准数据的不确定度根据由校准公式计算的最小二乘拟合值与实际加载量之间的残余误差的标准偏差进行评估，即

(11)

根据校准模型公式(1)给出的函数关系，以及由公式(11)确定的校准数据的精度，可得校准系数的协方差矩阵为

(12)

其中，任意校准系数aj的标准不确定度为

(13)

校准系数aj与校准系数ak之间的协方差为

(14)

由此，校准系数的不确定度可以综合反映校准实验中随机效应的影响。

3.3 工作测力组件输出的不确定度

由于多分量推力测量系统各测力组件输出的不确定度对于实验结果的最终不确定度有着极其重要的影响，为了对其测量不确定度评定做到客观准确，需要分别对各测力组件输出的不确定度进行单独评定。测力组件输出值的不确定度主要由以下两个部分组成。

① 工作测力传感器误差引入的不确定度。

在工作测力传感器的检定证书中，精度指标由线性度L、重复性R和滞后性H三项构成，假定以上三项不确定度来源相互独立，由此可以计算其校准不确定度为

(15)

② VXI系统测量通道误差引入的不确定度。

测量通道误差引入的不确定度uvxi可以根据VXI系统的产品说明书技术指标或现场检定结果确定。如果给出的为极限误差±Δ，且服从均匀分布，则

(16)

上述两项不确定度来源相互独立，于是可得测力组件输出的合成标准不确定度[25]为

(17)

由于缺少足够的信息以获取各测力组件输出的相关性，本文按所有测力组件输出之间的相关系数等于“1”进行处理。

4 校准实验及结果评定

4.1 校准实验步骤

具体的校准实验步骤如下：

① 将多分量推力测量系统的各个力/力矩分量按其设计量程分成8个以上的等间隔加载点，对各个分量按从小到大的顺序进行加载和卸载，各重复3遍。

② 按正交设计原则设计了64组复合加载表，重复加载和卸载3遍。

③ 选取15组验证载荷进行加载，重复3遍以上，选取的验证载荷可以为单分量加载或复合加载，选取时应尽量模拟多分量推力系统的真实工作状态。需要说明的是，在后续的数据处理中，这15组加载数据只用于校准公式验证，不用于校准系数的求解。

4.2 校准实验结果

利用上述校准加载系统以及实验方法，对研制的多分量推力测量台架进行了静态校准实验。实验采用的工作测力组件输出的不确定度评定结果如表1所示。

表1 工作测力组件输出的不确定度

基于最小二乘原理，通过全回归分析方法分别得到了一阶校准公式和二阶校准公式，并通过逐步回归分析方法对二阶校准公式的自变量项进行了取舍，取舍后的校准系数个数为96个。其中，一阶校准系数矩阵[A]6×6的计算结果如式(18)所示，评定得到的校准系数矩阵中各系数的不确定度数值如表2所示。

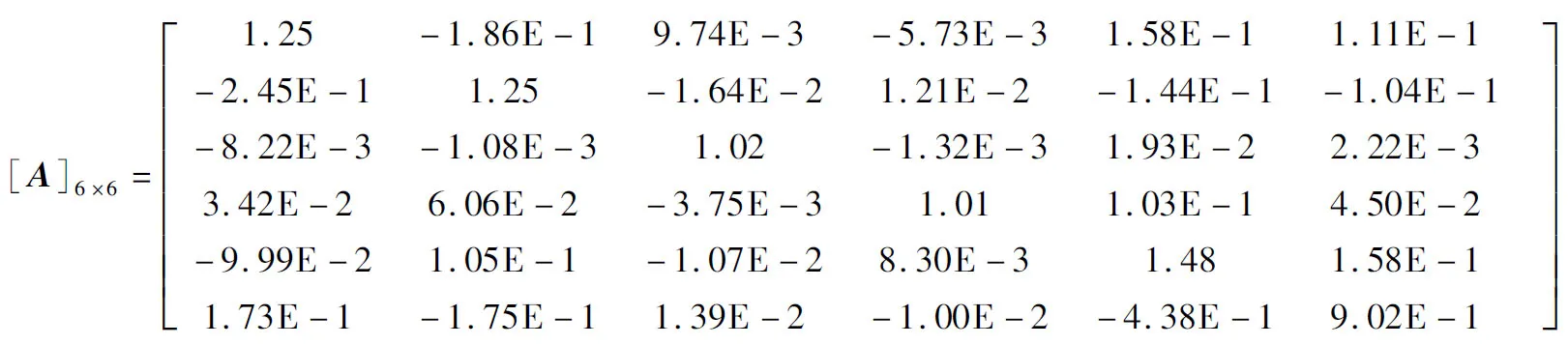
(18)

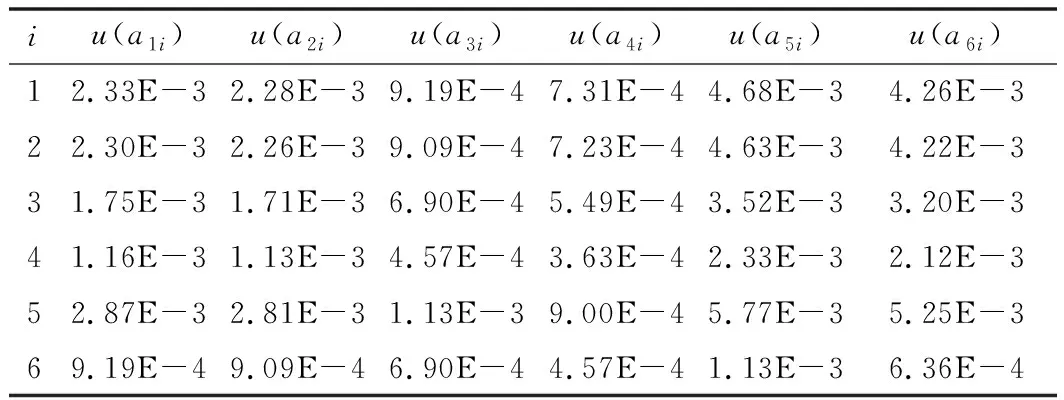
表2 一阶校准系数矩阵中各系数的不确定度数值

首先采用传统方法对多分量测量系统的性能进行评定，图4(a)、图4(b)分别给出了应用一阶校准公式得到的各力分量的校准残余误差和验证残余误差，图5(a)、图5(b)给出了应用二阶校准公式得到的校准残余误差和验证残余误差。

将采用传统方法得到的误差评定结果汇总，如表3所示。可以看出：① 校准残余误差与验证残余误差都随着数据点(或加载条件)的不同呈无规律变化；② 对于各个力分量，验证残余误差总体上略大于校准残余误差；③ 由于采用了更多的自变量项、考虑的干扰更加全面，相较于一阶模型，二阶模型具有更小的校准残余误差和验证残余误差；④ 无论是校准残余误差还是验证残余误差对于测量系统结果精度的描述都极其依赖于加载点的选取。

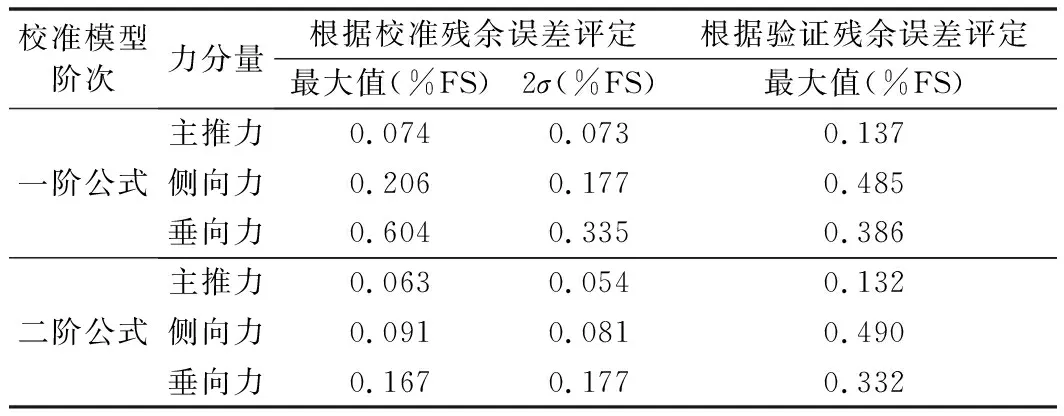
表3 传统方法得到的误差评定结果

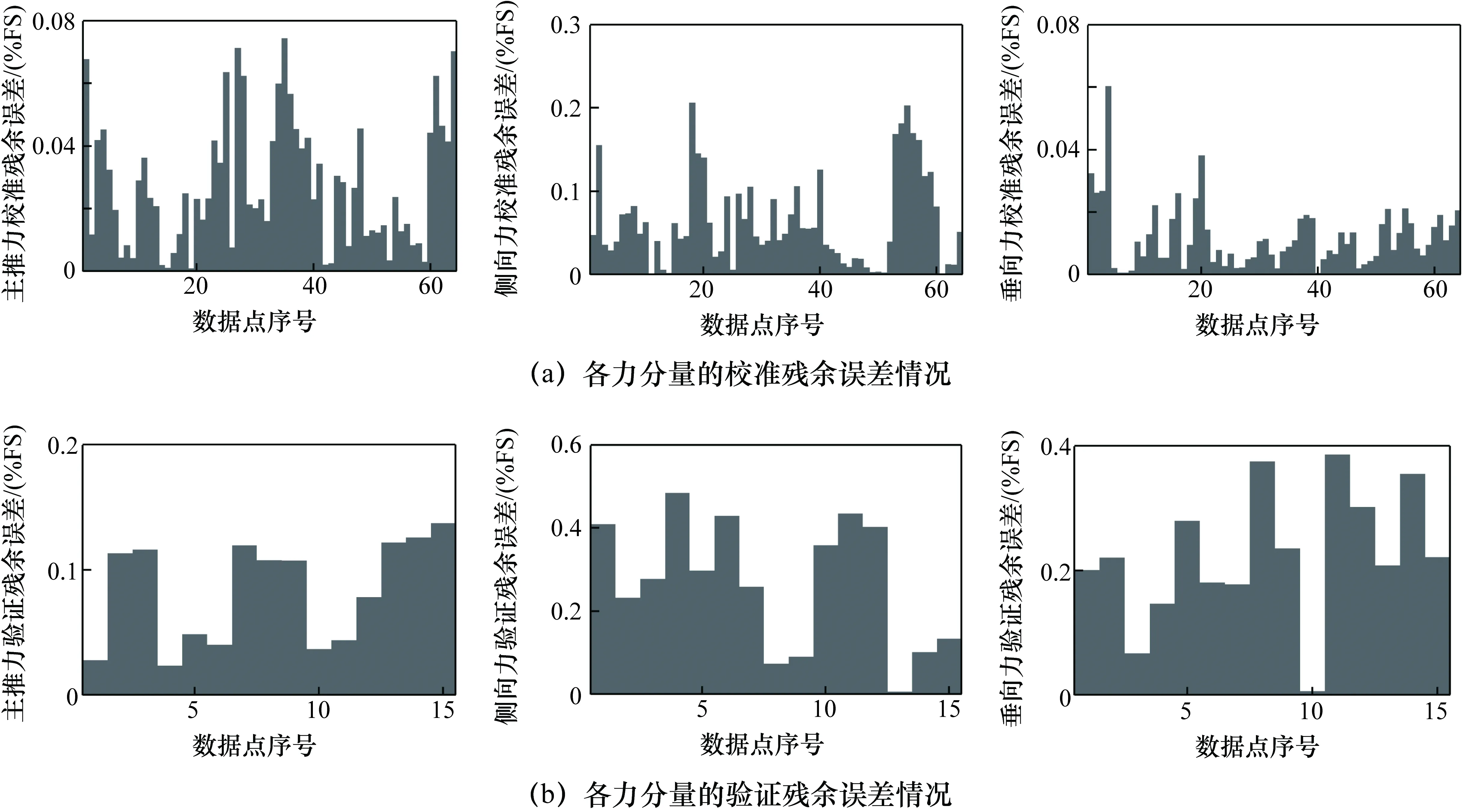
图4 一阶校准公式的校准残余误差与验证加载残余误差

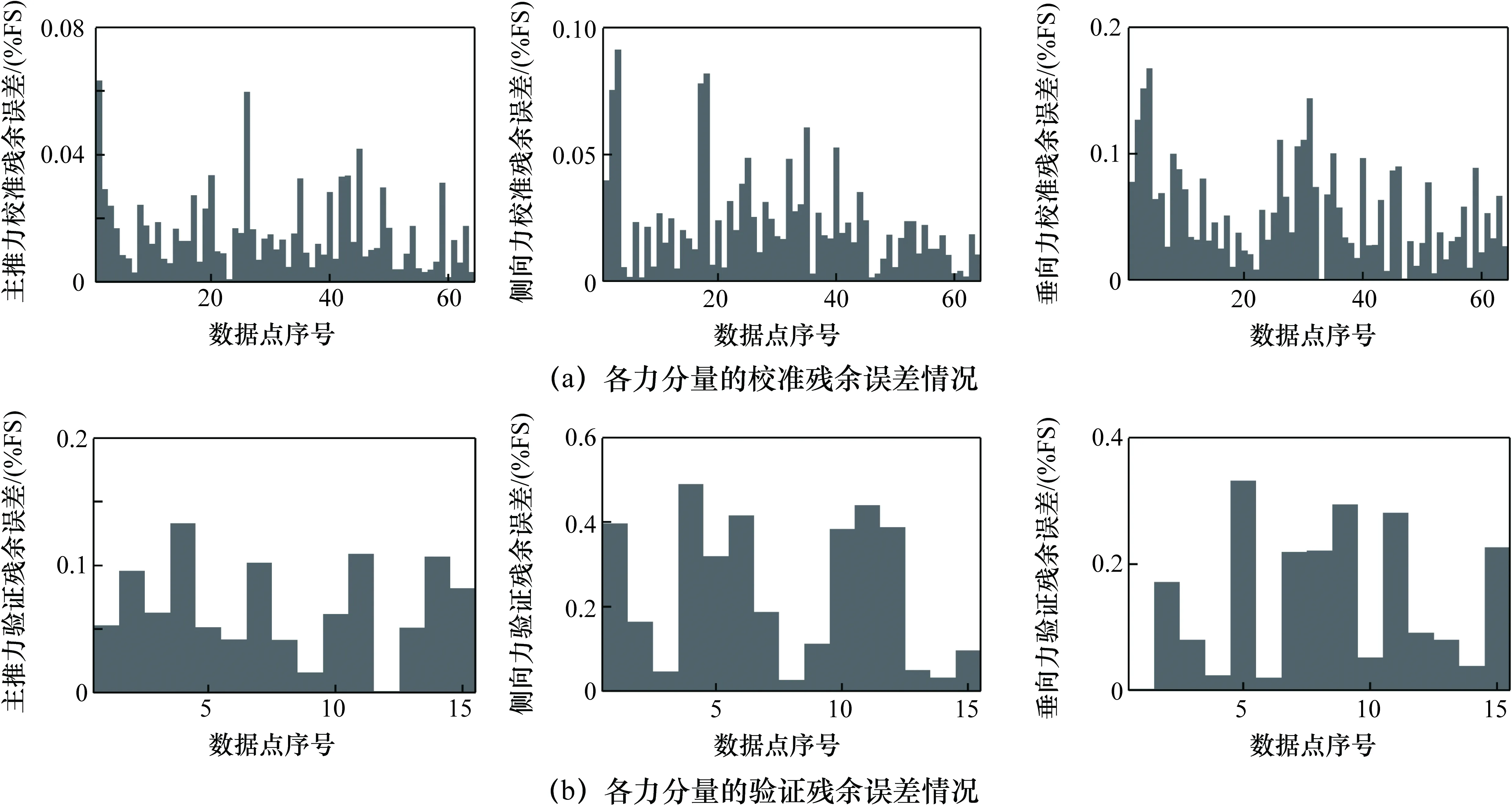
图5 二阶校准公式的校准残余误差与验证加载残余误差

4.3 不确定度评定与比较

采用基于校准系数误差传递的评价方法，对校准模型公式计算的各个实验加载点的测量结果进行评定，分别得到了各个力分量随加载条件变化的不确定度。将该结果与传统方法的评定结果进行比较，如图6所示。图中，前64个数据点为校准实验点，后15个点为验证实验点，Cal_2*Stdev表示根据校准残余误差的相对标准偏差得到的不确定度，Cal_MaxError表示采用校准残余误差的最大值得到的不确定度，Ver_MaxError表示采用验证残余误差的最大值得到的不确定度。

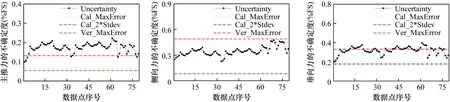
图6 各力分量测量不确定度评定结果对比

若定义不同实验加载点测量结果不确定度的最大差异Δumax为

Δumax=(umax-umin)/umax×100%

(19)

那么，对于主推力分量测量，在实验加载点61的测量不确定度最大，为0.22%FS，在实验加载点1的测量结果不确定度最小，为0.10%FS。由式(19)可得主推力在不同实验加载点测量结果不确定度的最大差异为55.3%；类似地，侧向力和垂向力在不同实验加载点测量结果不确定度的最大差异分别为52.6%和49.1%。

显然，3个力分量测量结果的不确定度均随着实验加载点的不同而不同，且存在较大差异。这是由于测量结果的不确定度同时来源于校准系数的误差和测力组件输出的误差，其中校准系数引入的不确定度是会随着加载力的变化而变化的。本文采用的不确定度评定方法克服了传统方法无法反映加载条件变化对测量结果精度的影响的缺陷，因而对于测量结果的精度表征更加科学合理。

总体来看，研制的矢量推力测量系统在各力分量的测量中均具有较高精度，校准实验结果验证了本文采用的静态校准方法是可行的，针对矢量推力测量系统精度评定问题研究的不确定度评定方法是非常有效的。

5 结束语

校准工作是航空发动机矢量推力台架建设和使用过程中必不可少的关键步骤，其准确性直接影响到矢量推力测量系统工作性能的好坏。本文针对矢量推力测量系统的静态校准方法展开研究，建立了系统的一阶、二阶校准模型，并通过多元线性回归分析得到了各阶模型的校准系数。在此基础上，提出了一种基于校准系数误差传递的不确定度评定方法，与传统的结果评价方法相比，该方法可以有效评估随台架工作载荷变化的测量结果不确定度区间。

① 系统校准实验结果表明，研制的航空发动机多分量推力测量系统在各方向测量不确定度均优于0.5%，具有较高的精度，本文采用的静态校准方法是完全可行的。

② 实验结果同时表明，推力测量台架在不同载荷条件下的测量不确定度有较大差异，实验中各加载条件下的不确定度差异最大可达55%，工作载荷是影响系统测量结果精度的重要因素。因此，研究推力测量系统面向测量任务的不确定度评价方法，准确反映台架工作状态对测量结果的影响，对于矢量推力测量系统性能的科学合理评定、促进矢量推力测量系统精度提升具有重要意义。