双天线测向信息辅助捷联惯导快速对准算法

刘俊杰， 陈 健， 贾继超， 商 阳

(1.航空工业陕西飞机工业(集团)有限公司，陕西 汉中 723200； 2.中国航天科技集团公司第九研究院第十六研究所，陕西 西安 710100； 3.航空工业西安飞行自动控制研究所，陕西 西安 710076)

快速对准技术作为惯性技术领域的一项关键技术，一直是各国武器装备技术研究的热门之一[1-5]。本文针对高精度惯导的快速对准问题，研究双天线辅助实现惯导快速对准的算法方案。

正常罗经对准主要包括水平对准和方位对准，而方位对准主要是基于通常所说的罗经效应，需要比较长的寻北时间，从而限制了整个对准时间。罗经对准具体实现采用卡尔曼滤波器，初始对准的基本思想是利用惯导系统的速度、姿态角误差方程，分析引起误差的主要因素，然后通过卡尔曼滤波器估计姿态误差并进行修正，从而达到惯导系统初始对准的目的[6]。但这种基于罗经效应的对准算法耗时较长，难以满足战机快速出动需求[7-8]。采用位置、速度量测的对准方案虽然可通过载体机动加快航向收敛速度，但载体提出了运动约束条件，另外静态情况下也无法实施。

外部航向引入对准方式航向收敛快，如静基座情况下的输入航向对准方式。在低精度系统中，由于无法自寻北，这种航向引入方式也在广泛使用。目前，双天线测向信息在低精度组合系统中已得到较广泛的应用，但测向精度受限于测量基线及安装偏角等导致的空间配准问题，在高精度系统中的应用未见报道[9-12]。引入双天线卫星载波相位差分测向信息后，对准时主要根据速度、位置量测进行水平对准，方位对准直接采用航向观测量进行观测，这种对准方式相对正常罗经对准时间极大缩短。

本文首先分析了双天线基线安装角偏差对准航向测量的影响，给出了相应的标定补偿算法。在传统速度、位置量测对准算法的基础上，给出航向观测方程，构建了双天线测向信息辅助的双天线卫星测向辅助的快速对准算法。在地面进行静态、动态测试获得双天线测向误差特性，基于实测的双天线测向误差特性，对快速对准方案进行了半实物仿真验证。设计的双天线辅助快速对准算法及仿真验证结果将为后续工程提供参考。双天线测向为绝对航向测量方式，仅需在载体上增加设备，无需额外的对准辅助设备，对准精度高，使用方便，可作为运动载体应急出动时的一种对准方式使用。

1 双天线测向

卫星测向基本原理如图1所示，由两个测量型卫星导航天线沿机体纵轴安装。

ψ=-arctan2(xL,yL)

(1)

图1 卫星测向原理示意图

根据误差传播关系有

(2)

2 双天线辅助对准算法

2.1 安装误差补偿

当双天线基线与机轴不重合时，双天线测量的航向与载机航向之间存在偏差，且偏差随着载机俯仰、横滚角的变化而变化。双天线基线与机轴角度偏差越大，由载机俯仰、横滚角变化引起的波动越大[13]。考虑俯仰角、横滚角需在对准一定时间后才能有较高精度，才能保证航向偏差的补偿精度。因此，需要在机械结构安装中使双天线基线与机轴尽量重合，以保证对准初始航向安装偏差的补偿精度，满足快速对准需求。

具体标定可通过以下3种方式实现。

① 直接标定方式。直接标定惯导与双天线基线之间的安装偏角，具体实现时可通过静止状态下惯导、双天线多次测量的俯仰角、航向角均值计算俯仰、航向安装偏角。

② 间接标定方式。分别标定惯导相对机体轴、双天线相对机轴的安装偏角。具体实现：通过架平飞机，读取传感器数据进行计算。

③ 几何测量方式。直接通过双天线的几何坐标，计算双天线基线相对机轴的角度关系。

通过以上标定可获得具体安装偏角补偿参数λX，λZ。λX，λZ为以惯导输出轴为基准，按右手法则转动至双天线测量基准所要转动的角度。

具体航向误差补偿公式为

(3)

式中，θ,γ分别为捷联惯导的俯仰角和横滚角。获得双天线的航向信息后，先补偿安装误差：

ψ′=ψ-Δψ

(4)

2.2 对准滤波器

采用滤波器增广航向量测方式，在传统速度位置量测对准的基础上加航向观测量。

先进行简单粗对准，以一段时间惯导输出的平均比力计算姿态阵的第3行元素，再根据第3行元素计算粗略俯仰、横滚角。

(5)

(6)

结合双天线航向角ψ的3个完整姿态角度，完成粗对准。

对于捷联惯导系统，导航坐标系选为“东北天”地理坐标系，降阶对准算法一般考虑其数学平台误差、速度误差、位置误差、陀螺随机常值漂移和加速度计随机常值偏置，认为惯性测量组件的其他误差项及惯性系统与辅助卫星导航系统之间的时空差异已经得到很好的校正。选取双天线航向信息辅助对准的滤波状态向量x为

(7)

根据捷联惯导误差方程和器件误差参数模型，可列写出降阶对准的状态方程为[14]

(8)

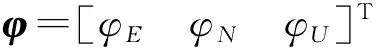
以惯性导航系统输出速度、位置与卫星导航系统的速度、位置的差值作为量测量，速度、位置量测方程为

(9)

以惯性导航系统航向与卫星导航系统双天线航向的差作为量测量，航向量测方程为

yψ=δψ

(10)

由式(9)和式(10)可得最终对准量测方程为

(11)

式中，v为量测噪声。式(8)和式(11)组成了常用空中对准的降阶卡尔曼滤波模型。具体量测处理时可采用序贯处理或集中处理方式。

3 仿真及分析

仿真思路首先根据地面测试获得双天线测向的误差特性，将其误差注入仿真模型进行仿真分析。在地面室外静态、跑车转态下进行多组试验数据采集。典型地面双天线测向静态、动态误差特性如图 2和图 3所示。

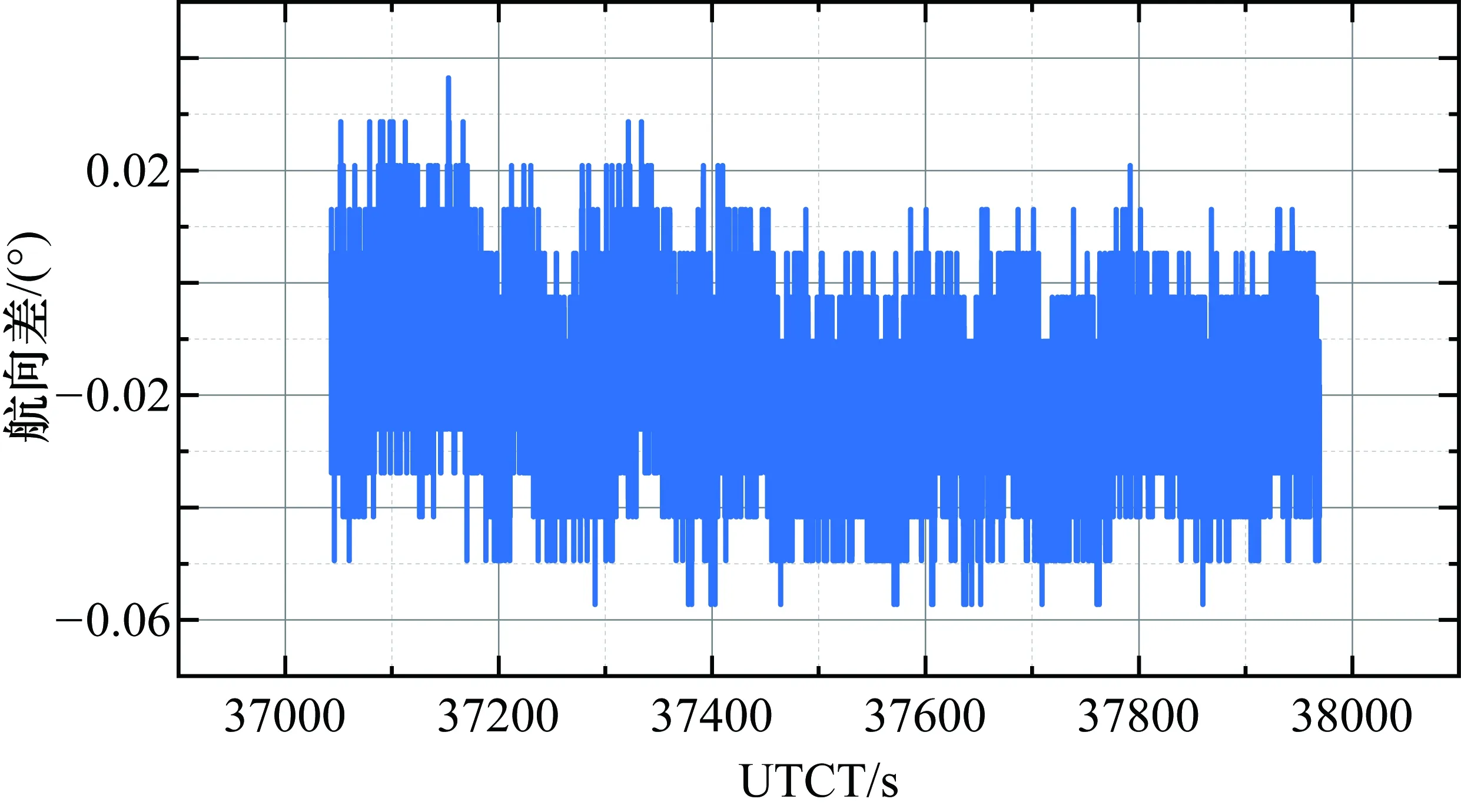
图2 静态数据

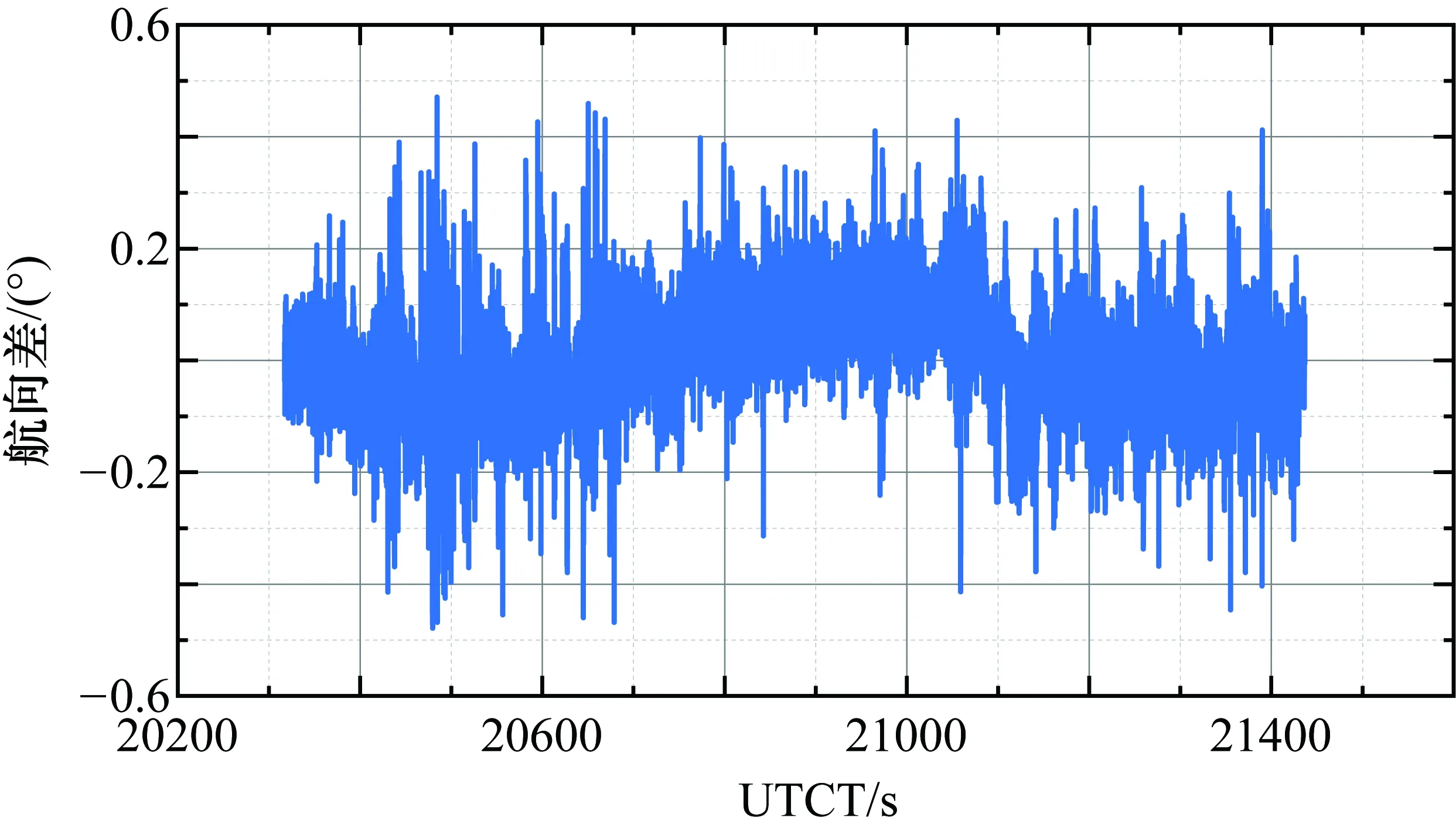
图3 跑车情况航向差

由图2可知，静态情况下较理想，航向误差的均方根(RMS)值为0.022°。由图3可知，动态情况下航向差值相对变大，RMS值为0.095°。

假定惯性测量组件误差状态仿真参数如表1所示。由于对准时间短，惯性测量组件误差状态按随机常值建模。

表1 仿真惯性测量组件误差状态

根据以上两组航向测量误差数据分别仿真静态对准、动态对准性能，得到航向对准精度如图4、图5所示。

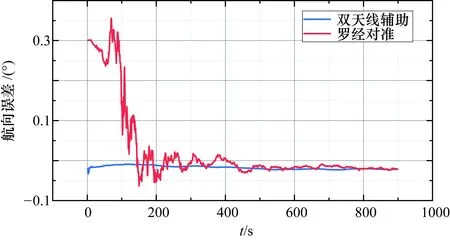
图4 静态双天线辅助对准航向误差

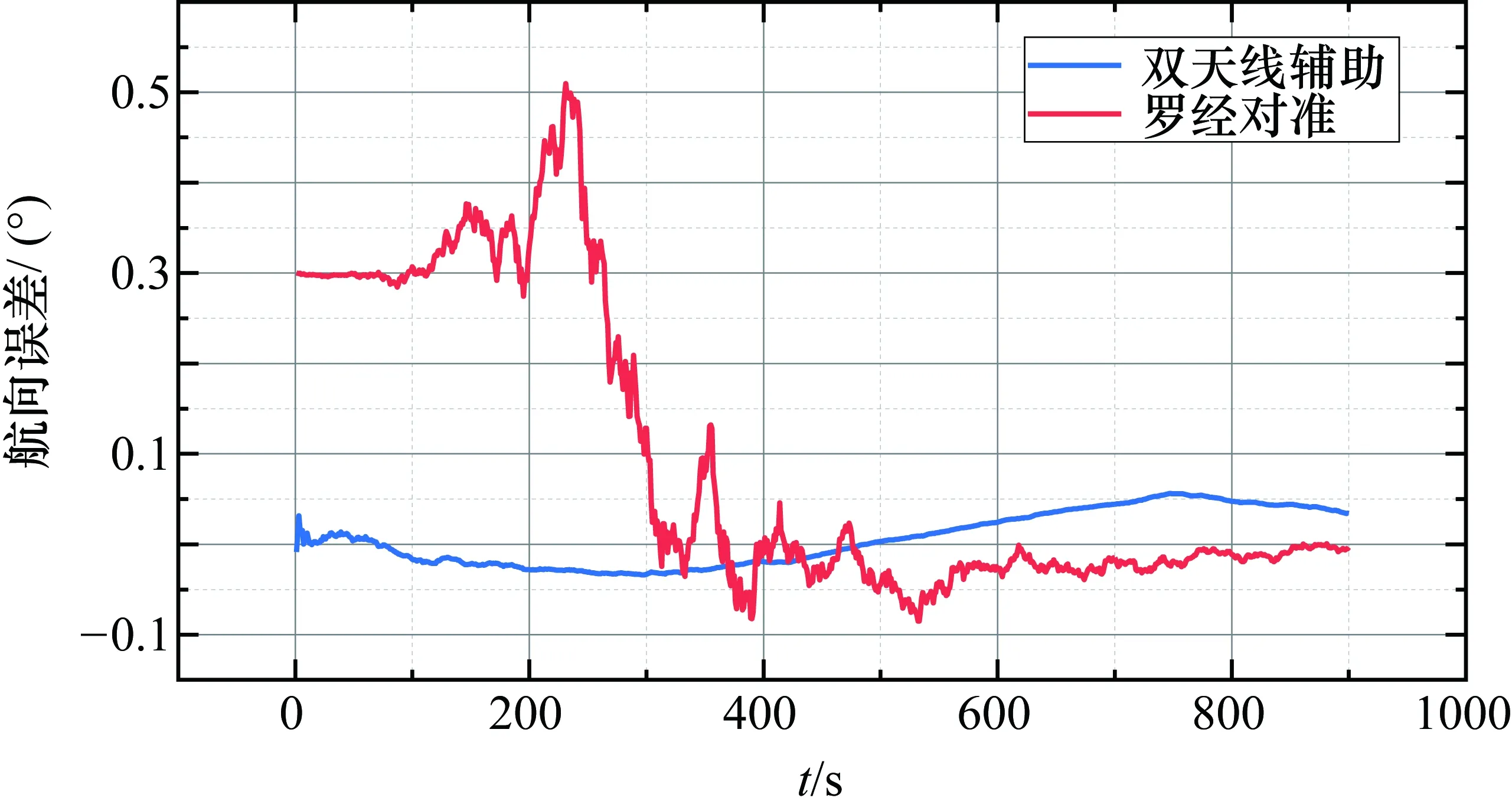
图5 动态双天线辅助对准航向误差

由图4、图5可知，引入双天线航向后，相对传统罗经对准航向收敛速度明显加快，在3 min内可收敛至0.05°以内，可满足标准0.8 nm/h捷联惯导的快速高精度对准要求。跑车时若双天线航向误差存在一定的波动(如图3所示)，将导致对准过程中航向误差也存在一定的波动(如图 5所示)。因此这种辅助对准方式具体对准精度受双天线航向精度影响较大。

4 结束语

双天线辅助对准属于外部航向引入的一种对准方式，可极大地缩短捷联惯导航向对准时间。若同时有卫星速度、位置数据，可在动基座情况进行捷联惯导的快速对准。卫星测向航向引入方法，为绝对航向测量方式，仅需在载机增加设备，相对其他的航向引入方式如等局部基准、光学方式等使用简单。双天线基线与机轴角度偏差越大，由载机俯仰、横滚角变化引起的波动越大。考虑俯仰角、横滚角需在对准一定时间后才能有较高精度，需要双天线基线与载体机轴机械结构安装上尽量重合，从而保证对准初始时航向安装偏差的补偿精度，满足快速对准需求。动态情况下，载体可能存在较大的角速度，航线观测对时间同步的要求较大，需设计高精度的时间同步机制。