低液位非满管流量校准及其测量影响因素分析

刘 瑛， 陈 旭， 徐明刚， 陈银银

(北方工业大学 机械与材料工程学院，北京 100144)

非满管流量测量在市政排污、农业灌溉、废水处理等领域中被广泛应用。非满管指液体未充满管道的状态，管内为气液混合物。在实际情况中，液体流经管道时，很难不留空气的充满整个管道，同时管道的管壁厚度、截面尺寸、电极之间间距等因素的变化，都很可能引起管内液体的液位变化[1]。

非满管电磁流量计最早于20世纪90年代被Fisher & Porter公司研制成功[2]。它的出现，使管道横截面为圆形情况下的非满管流量测量精度得到提高[3]。目前，非满管流量测量主要通过德国科隆公司的TDALFLUX、ABB公司的Pati-MagII、上海大学的非满管流量测量系统[4～7]进行流量测量。流量测量的主要参数是管道内流体的液位高度和平均流速，文献[4]～文献[7]所述流量测量方法均是通过测量主要参数进行流量测量的，但其电极必须位于被测流体中，流体液位高度为较低充满度时(管道直径的10%)，电极无法全部浸入到被测流体中，难以实现对信号的采集[7-9]。

为解决上述问题，本文提出了一种低液位非满管流量测量方法：基于连通管原理结合高精度激光测距仪测得流体液位高度值，管道上方通气管结合流速仪精确测量管道内流体平均流速，通过体积流量计算公式得到流量值。

影响流速的因素有流体黏度和管道粗糙度，文献[4]～文献[7]所述流量测量方法均未对流体黏度和管道粗糙度进行分析。晏飞等[10]基于Herschel-Bulkley模型，运用CFD对润滑脂的流动进行数值模拟，得到黏度和速度的关系分布规律。Santos[11]通过玻尔兹曼方程和Bhatnagar-Gross-Krook动力学模型对简单纵向流动中的黏度和速度进行了分析，得到黏度和速度的非线性函数。张桂欣等[12]、高杨等[13]分别应用激光测距仪和三维超声波流速仪，得到粗糙度和速度的分布规律。

本文运用FLUENT仿真软件对管道粗糙度和流体黏度进行模拟，建立粗糙度-平均流速、黏度-平均流速模型，分析出粗糙度、黏度与流量的具体关系，通过多次实验验证模型的准确性及测量方法的可行性。预计本文提出的测量方法适用于流体液位高度为较低充满度时(管道直径的10%)的流量测量，对低液位非满管流量测量的发展与创新具有重要意义。

1 流量测量原理

管道中间部分平均流速的测量：将流速传感器经管道中间上方通气管放入待测流体中，旋桨位于当前液位高度的50%～60%，进行平均流速的测量。测量原理为

(1)

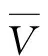
测量平均流速时，桨叶在水力推动作用下旋转，内置信号装置产生转数信号，桨叶水力螺距K和流速仪常数C均为常数，测流历时T和该时段内产生的信号数N测得后，即可算出测流时段内的平均流速值。

管道内液位高度的测量：将激光测距仪垂直置于U型连通管正上方，连通管中置一浮漂，进行液位高度的测量。

根据连通管原理可得

ρ1·g·h1=ρ2·g·h2

(2)

式中，所测流体相同、密度相等(ρ1=ρ2)、两边压强一致时，管内液位高度与U型管内液位高度相等。基于此原理，可在不干扰管道内部流体流动的情况下，通过测量U型管内液位高度值，实现管道内液位高度的测量。同时，外置型的安装使激光测距仪的更换更加简便，降低了维修成本。

2 仿真分析

2.1 流量计算

根据体积流量公式可得

(3)

(4)

式中，D为管道内径，单位为m；h为液位高度，单位为m。

2.2 建立模型

在SolidWorks中建立进水管直径18 mm，管道直径100 mm，长3 m的圆形截面直管道，前1.5 m为湍流发展前置段。在Workbench中将建立好的模型导入Geometry中进行优化后，将模型导入Mesh中进行网格划分，划分方式为四面体网格，网格总数为1870715，管道中间部分网格划分如图1所示。对网格质量进行检查，最小体积为正值且最小正交质量为0.23，大于0.2，符合仿真网格质量要求，FLUENT中求解器选取分离式，采用SIMPLE算法，采用隐式算法。

图1 局部网格划分图

由于水、植物油和空气多相物质同时存在，因此选择多相流(Multiphase)下的VOF模型进行计算，流体介质包括空气、水、植物油，各介质基本参数如表1所示。

表1 介质基本参数取值表

设置进水口为速度进口，速度大小为0.4 m/s，设置湍流强度为5%，水力直径取入水管直径18 mm[15～16]。通气管为空气进口，U型管、水平管出口设置为压力出口，管道主体为固体壁面，采用无滑移边界条件，设置壁面粗糙度分别为0 mm，0.033 mm，0.049 mm，0.139 mm，0.150 mm，0.445 mm。在计算过程中，当管道内部流动形态变化较小时，认为流动趋于稳定，以此时计算结果作为最终流场进行分析。

2.3 仿真结果分析

对6种管道粗糙度及3种流体黏度进行仿真分析，管道1.4～1.6 m处的速度分布数据通过Origin进行拟合处理，得到粗糙度-平均流速模型和黏度-平均流速模型。粗糙度-平均流速模型见式(5)，拟合曲线如图2所示。

(5)

式中，Ra为粗糙度，单位为mm；A1，A2，A3为常数项，具体数值如表2所示。

表2 粗糙度-平均流速模型常数取值表

对粗糙度-平均流速模型进行分析，可得到流量与粗糙度的具体关系，见式(6)。

(6)

黏度-平均流速模型见式(7)，拟合曲线如图3所示。

(7)

式中，μ为流体黏度，单位为kg/(m·s)；B1，B2，B3为常数项，具体数值如表3所示。

图2 不同流体的粗糙度-平均速度曲线图

图3 不同粗糙度的黏度-平均速度曲线图

流体黏度μ与雷诺数Re的关系见式(8)。

Re=ρvd/μ

(8)

式中，Re为雷诺系数；ρ为流体密度，单位为kg/m3；v为流体特征速度，单位为m/s；d为特征长度，即流体液位高度h，单位为m。对式(7)、式(8)进行分析，可得到雷诺系数与平均流速的关系：

(9)

对黏度-平均流速模进行分析，可得到流量与黏度的具体关系：

(10)

表3 黏度-平均流速模型常数取值表

实际应用中，需增加数据查表功能。数据表存储不同介质及对应参数值，根据不同介质，选择对应参数。

3 实验与分析

3.1 实验平台

为验证测量方法的可行性，搭建实验平台，设计方案示意图如图4所示，实物图如图5所示。管道外置U型连通管，激光测距仪沿垂直方向朝下发射激光，激光终点为浮漂上表面，以此实现液位高度的测量。管道中间正上方焊接一个通气管，将流速仪垂直放入待测流体中进行测量，旋桨位于当前液位高度的50%～60%，液位不得低于旋桨直径的一半(6 mm)，测量信号经流量计算模型处理后得到对应流量值。

图4 实验平台设计方案示意图

图5 实验平台实物图

图4中实验器材如下。

① 自制0.5 m×0.5 m×0.5 m的不锈钢连通水箱；

同样是金枝玉叶的段誉，第一次来燕子坞吃的那些：“茭白虾仁”“龙井茶叶鸡丁”，看看就教人馋涎欲滴。段誉的当时心理评判是这样的：“鱼虾肉食之中混以花瓣鲜果，色彩既美，自别有天然清香。”

② 额定功率为250 W的水泵；

③ L20的弯头、溢流阀；

④ QS智能型电动调节阀；

⑤ 精度等级为±0.2%FS的DN20电磁流量计；

⑥ 精度等级为±0.01%FS的激光测距传感器；

⑦ 定制的U型连通管；

⑧ 长3 m、粗糙度0.15 mm的DN100标准镀锌管道以及配对法兰盘；

⑨ 精度等级为±1.0%FS的便携式流速传感器；

⑩ ARM公司STM32F103系列的微控制器信号处理单元。

3.2 实验测量

在μC/OS II操作系统下对信号处理单元进行编程，激光测距传感器的采集频率为5 Hz，每1 h采集一次流速传感器的测量值，信号处理单元将采集到的液位测量值进行均值处理，连续测量1 h后，经算法处理输出该时段的累计流量值，同时根据Modbus标准协议由串口向DN20电磁流量计发送指令得到1 h实际流过的流量值。

最后通过串口将计算值和电磁流量计的标准流量值发送到PC端，实验记录结果如表4所示。

表4 实验结果记录表

对电磁调节阀进行调节，使DN20电磁流量计流速显示0.4 m/s，与仿真进水口流速一致，进行测量实验。通过实验发现，调节阀开合度为28%时，DN20电磁流量计流速显示0.4 m/s。

表5 仿真结果与实验结果对比表

4 结束语

本文通过FLUENT仿真软件对低液位非满管流量测量影响因素进行分析，基于提出的测量方法进行实验，实验结果表明：

① 管道内液位高度不大于0.1D时，流量测量误差不大于0.85%，通过粗糙度-平均流速、黏度-平均流速模型计算得到的流量值，误差不大于3.03%；

② 实验验证了该方法的可行性和粗糙度-平均流速、黏度-平均流速模型的可靠性，适用于低液位的非满管流量计量。

本文创新点如下：

① 提出一种低液位非满管流量测量方法，实现对低液位流量的精确测量；

② 通过建立粗糙度-平均流速、黏度-平均流速模型，进一步得到粗糙度、黏度与流量的具体关系。

论文有待进一步解决的问题如下：

① 受流速传感器本身结构的影响无法对含大颗粒的流体进行测量，在对结构的优化方面有待进一步解决；

② 受实验室环境限制，无法对大口径管道进行模拟和实验，大口径管道的非满管流量测量有待进一步研究。