浅议初中学生数学解题能力的培养
周绪娟
(江苏省灌云县龙苴中学 222212)
数学学习一直是初中学生的学习重点,数学的解题能力的培养是数学教学的重点和难点.据调查,许多学生对数学学习中的解题经常出现错误,一些数学学习中有困难的学生更是对数学解题是“望而生畏”,看不懂题目内容,抓不住题目关键词,找不到科学的解题方法,缺乏有效的解题思路,同时还存在着计算能力偏差的状况.主要原因是平时缺少大量的解题训练,或者训练方法有误,以及教师没有注重培养学生解题能力.那么如何在日常数学教学中培养学生的数学解题能力呢?
一、紧扣基本概念,掌握基础题型解法
正确理解并掌握数学概念(包括定义、定理、公式等)的含义及其推导过程是学好数学知识的基本前提条件,是继续学习数学知识及解决数学问题的最佳保障.但是只掌握数学概念远远不够,教师还应基于教材,着重训练学生基础题型的解法,通过基础题型的训练,让学生在“学中做,做中学”,将基础题型与基本概念相结合,从而加深对数学基本概念的理解,同时在掌握基础题型的正确解题思路的基础之上,获得相应的初步解题技巧.
概念是理解教学内容的关键,也是学习解题的依据,要帮助学生学会解题,提高学生的解题能力,首要要帮助学生正确的理解概念,特别是数学学习中,数学概念是解题的依据,概念不掌握,就没有办法去理解习题的内容和找到解题的方法
例如在“探索全等三角形的条件”(苏科版八上第一章第三节)部分的解题训练中,教师应结合学生的日常生活,从生活实例中设计一些学生能“看懂”的基础题型(注意这部分题目不能太难,应以考查学生对基本概念的正确掌握程度,以及基本概念的推导过程为主),让学生通过基本题型的训练,进一步加深对基本概念的理解.
如教师可以这样设计:(1)△ABC与△ABD为全等三角形,请写出哪三个角一一对应相等?哪三条边一一对应相等?(此题主要考查“如两个三角形全等,则三条对应边相等且三个对应角相等”,着重考查如何确定“对应角、对应边”);(2)若△ABC与△ABD全等,则成立的必备条件有几种形式?并写出具体成立条件.(此题主要考查判定两个三角形全等有几种方法,以及从哪个角度思考判定两个三角形全等的方法,着重考查“夹角”的概念及确定);(3)两个全等三角形△ABC与△ABD面积相等,反之能成立吗?如不成立请说出你的理由,并说出使之成立应增加什么条件,共有几种增加方法.(此题主要考查三角形全等的性质以及运用,着重考查学生对于三角形全等的判定及性质的基本综合应用能力,以及初步培养学生的反向推导能力).通过结合基本概念的基础题型的训练,可以有效加深学生对基本概念的理解及综合应用能力的提升,培养学生对学好数学的信心.
二、正确审清题意,掌握题型综合解法
做题必须先审题.在数学解题能力中,审题能力作为必备能力,教师在培养初中生解题能力过程中,应着重培养学生的审题能力,部分学生没有养成解题先审题的良好习惯,结果边解题边审题,不仅浪费了大量时间,解题效果也不甚理想.因此,教师在解题训练中应引导学生养成解题先审题的良好习惯,同时在训练中掌握各类题型的综合解法.
例如在“中心对称与中心对称图形”(苏科版八下第九章第二节)部分的解题训练中,教师可以设计部分针对提升审题能力的综合题型(这类题目以培养学生审题能力为主,同时让学生在训练中掌握相关类似题型的解法,形成一定的解题能力,因此在设计中要注意题目条件的外显及隐藏),让学生在训练中学会正确审清题意,同时学会一题多解及多题一解,掌握题型的综合解法.如教师可以设计这样的题目:(1)△ABC与△ACD为全等三角形,它们是中心对称图形吗?在什么条件下它们关于中心对称?(此题涉及三个知识点,即全等三角形的定义、中心对称图形的定义以及关于中心对称的定义,并将三个知识点有机结合在一起,学生在审题时将关键词“中心对称图形、中心对称”提炼出来,则此题可以顺利解答,若未认真审题,则可能出现错误解答);(2)平行四边形ABCD中的对角线AC、BD相交于点O,请问其中有几对图形关于中心对称,并一一列举(此题学生可以轻松找出△ABO与△CDO、△BCO与△DAO两对图形关于中心O点对称,却会没注意当对角线AC、BD相交于点O时,共出现4个明显可见三角形,4个隐含三角形,因此在列举时出现遗漏,此类题型可以训练学生在审题时注意题目中出现的隐藏条件).教师在设计及训练学生审题能力时,还应注意所设题目可有多种解法,以及相类似题目可用一种解法,从而让学生在训练中学会从不同角度去解题,提升综合思维能力,掌握同类题型的解题思路,从而提升综合解题能力.
三、加强习题训练,养成良好的练习习惯
要学生多做数学练习,是提高学生解题能力的关键和主要途径,但并不是习题做的越多越好,不能用题海战术去培养学生的数学解题能力.实践证明,其实,数学不是多做一些题就可以将自己的分数提升,而是要了解解题的方式,只有这样才能快速的整理出答案,这个科目是一种对脑部的思维能力的锻炼,因此我们可以在平时的生活中对孩子的这种能力进行锻炼.例如,在教材中的每一个单元,都有一定的数学习题.还有许多课外练习,特别是数学学科,各种练习习题多如题海,要只靠习题去提高学生的解题能力,那就会越做越多收效就不会很好.对于学生来说,数学科目就是一个题海,数学练习就是一坐雪山,火海,很多的家长都非常害怕看到孩子的数学作业和练习,但许多家长也想不出好的办法去辅导学生,明知不好还强迫学生去多做习题.很多家长都会对孩子使用题海战术,其实这是错误的,学校和老师,特别是数学教师需要明白学习数学并非是要去做题,如果让孩子做大量的题很容易会让孩子对数学产生厌恶和为难情绪,产生反感.
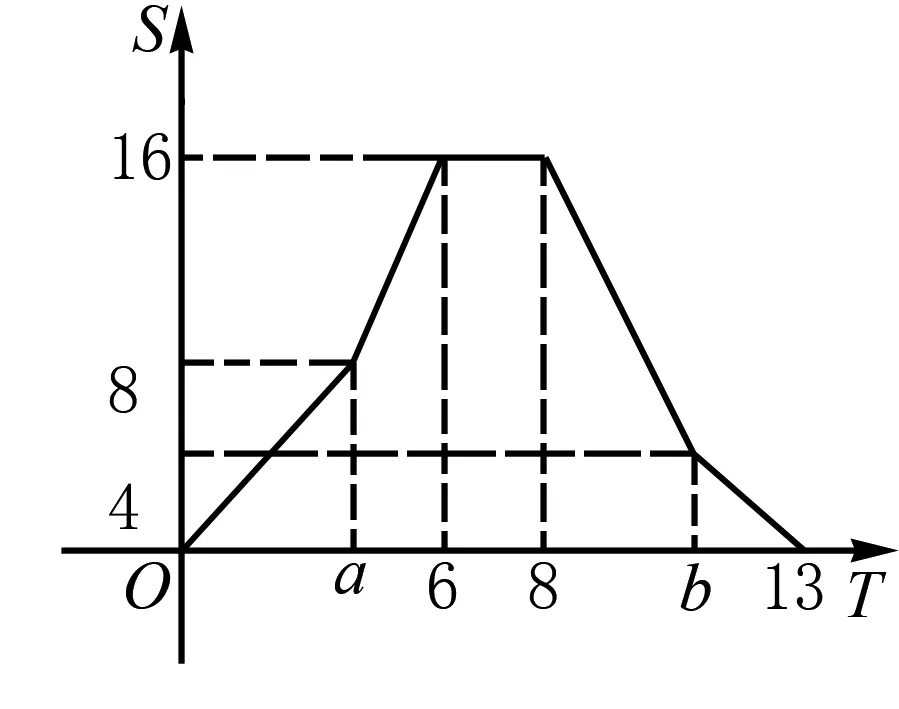
例如,在长方形ABCD中,点P从B点出发沿着四边按B→C→D→A方向运动,开始以每秒M个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后又恢复为每秒M个单位匀速运动.在运动过程中,△ABP的面积S与运动时间T的函数关系如右图所示.求长方形ABCD的长和宽.
这一类时间与速度的数学习题是典型的代数与几何相结合的数学习题,在所有的初中数学练习中,有很多这样的练习,在教学和练习中,我们要学会选择,选择典型习题去指导学生学会解题方法,不能反复的重复练习.虽然是重点和难题.但做的过多,过于反复练习,就会使学生失去学习兴趣.
古人曾经说过:“学而不思则罔,思而不学则殆.”其实质与数学教学中所提倡的“学思结合”思想理念一脉相通.教师在训练、培养、提升初中生解题能力过程中,还应积极引导学生在解题过程中不断反思,对解题过程中的经验及教训进行及时性的总结,养成归纳总结的良好学习习惯.
例如在“勾股定理的简单应用”(苏科版八上第三章第三节)部分教学目标为(1)用勾股定理及Rt△判定条件解决日常生活问题;(2)构造Rt△及结合方程求边长;(3)初步感受数学中“转化思想”(即将一个问题转化为另一个问题,从而有效解题的思想).教师在培养学生解题能力过程中,可以从三个方面引导学生不断反思总结,养成归纳总结的良好习惯:
(1)审题过程.是否抓住题目关键词语(如题目给出的“斜边”“投影”“周长”“面积”等关键词语)?隐含条件(如∠A=90°即提示为Rt△)是否已经挖掘出来?是否将关键词语和已知条件建立有效关联(如出现“斜边”及“中线”则需构建Rt△)?
(2)解题过程.在解题过程中主要反思解题思路是否正确,解题步骤(如计算过程、证明步骤)是否有遗漏;
(3)解题结果.在解题结果阶段主要查找错误(如计算结果错误)、遗漏(如遗漏回答)原因,并对此归纳总结.教师在培养学生解题能力的过程中,应着重培养学生养成反思、归纳、总结的良好习惯,让学生在不断的反思中总结解题经验,归纳总结解题方法,长此以往,学生才能在不断的反思、归纳、总结中形成自己的解题方法,提升自己的解题能力.
在数学教学中,老师和家长一定要记住这一点,培养学生的解题能力不能只靠题海战术.数学练习是培养学生数学解题能力的重要途径,但做习题也并非说是多做题,而是掌握解题的方法,我们不能忽略掉理论知识,我们要对学习到的公式等等进行整理,在闲暇的时候看一看、背一背,这样我们对公式和原理有更为深刻的理解.
教师在培养学生数学解题能力过程中,应基于“学思结合”“学以致用”的教学理念,结合生活实践,从教学目标出发,通过长时间、有计划的训练,可以有效提升学生的数学解题能力,养成良好的数学学习习惯.

