给定悬挂点数和谱半径最大的连通k一致超图的结构
朱忠熏,杨禹,周鋆鹏
(中南民族大学 数学与统计学学院,武汉 430074)
随着大数据时代的到来,承载着高阶高维数据信息的张量引起了学者的广泛关注.类似于矩阵与图,张量与超图间亦存在着一一对应关系.基于图谱理论研究和应用的成功经验,超图谱理论的研究及其应用逐渐成为国内国际相关领域学者追逐的热点问题.目前,超图谱理论的最新结果不断涌现,比如文献[1-5].本文致力于一类阶为n且具有r个悬挂点的k一致连通超图极值结构的研究,对n-r=1或2,k-3≤n-r≤k-1的情形,文献[6]刻画了其对应的极值结构,进一步地,本文将研究n-r=k-4的情形.
1 准备知识
设G=(V(G),E(G))是一个超图,其中V(G)为点集、E(G)为边集,且E(G)包含于幂集2V(G).对任意的e∈E(G),|e|=k,则称G为k一致超图.如点u,v同含在一条边中,称点u,v相邻.如v∈e,则称点v与边e关联.点不同且边也不同的点边交错序列称为一条路;如其第一个点和最后一个点相同,而其它点均不相同,称此点边交错序列为圈.如果G中的任意两个点间均有一条路,称G是连通的.
对于正整数k≤n,张量T=(Ti1i2…ik)是一个k阶n维数组,其中ij∈{1,…,n}=[n],j∈[k].如果对于下标的任意置换σ有Ti1…ik=Tσ(i1)…σ(ik),称张量T是对称的.对n阶k一致超图,其邻接张量[7]A(G)=(ai1…ik),其中:

取n-r≤k-1,r=s(k-n+r),设Cn,r是一个阶为n且恰有r个悬挂点和s条边的超图,其每条边均有k-n+r个悬挂点.
引理1[6]设1≤n-r≤k-1,r=s(k-n+r),如G在阶为n且具有r个悬挂点的k一致连通超图类中谱半径最大,则G≅Cn,r.
取r=s(k-n+r)+1,设Dn,r是一个阶为n且恰有r个悬挂点和s条边的超图,其仅有一条边含k-n+r+1个悬挂点,其余边均有k-n+r个悬挂点.
引理2[6]设1≤n-r≤k-1,r=s(k-n+r)+1,如G在阶为n且具有r个悬挂点的k一致连通超图类中谱半径最大,则G≅Dn,r.

引理3[6]设3≤n-r≤k-1,r=s(k-n+r)+2,G在阶为n且具有r个悬挂点的k一致连通超图类中谱半径最大.



引理4[6]设1≤n-r≤k-1和r=s(k-n+r)+t(0≤t (1)s=2和t=0,或s≥3; (2)G中恰有s条边,每条边至少含有一个悬挂点; 引理5[8-10]设x是连通k一致超图G的主特征向量,vi,vj∈V(G).如果vi∈e意味着vj∈e,e∈E(G),则xvj≥xvi.进一步地,如果有一条边仅含有vj而不含vi,则xvj>xvi. 定理1 设4≤n-r≤k-1,r=s(k-n+r)+3,s≥4,如G在阶为n且具有r个悬挂点的k一致连通超图类中谱半径最大,则: 由上述方程组可得: (1) (2) (3) (4) 由上述4个式子可得: 同理,可以得到: 定理3 设4≤n-r≤k-4,n-r=k-4,G在阶为n且具有r个悬挂点的k一致连通超图类中谱半径最大,则: (1)如果r=0(mod 4),则G≅Cn,n-k+4. (2)如果r=1(mod 4),则G≅Dn,n-r+4. 对于n-r=k-4的超图情况,首先得出了r=s(k-n+r)+3时具有最大谱半径的4种超图,当超图的边数s≥4时,超图的谱半径都可以求出,但是当边数s=3时,由于特征方程问题仅能确定有最大谱半径的超图是上述结果二者之一.因此,当n-r=k-4时,根据悬挂点的不同就能得出相应的有最大谱半径的k一致连通超图.
2 主要结果

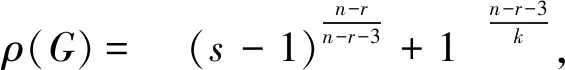
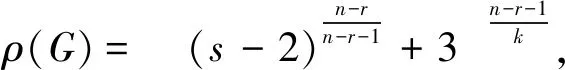

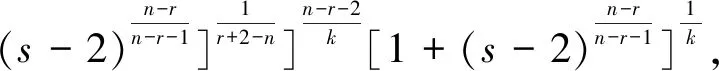





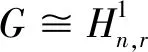

3 结论

