SV形态滤波的参数优化问题
段汕,刘丹,周奇鱼
(中南民族大学 数学与统计学学院,武汉 430074)
SCHONFELD D和GOUTSIAS J在文献[1]中提出了基于固定结构元的形态滤波理论和计算,主要研究了适用于图像恢复的形态滤波的算子优化问题和形态滤波的参数优化问题.在此基础上,文献[2]研究了基于SV形态学理论的滤波优化问题,通过建立SV形态模式谱和引入集差距离函数,在对结构映射和滤波的选取加以相关条件限制的情形下,在有效恢复图像与保持原始图像基本结构之间寻求一个平衡,从理论上证明了一类SV交替滤波和一类SV交替惯序滤波[3]是SV形态学方法下适用于噪声图像恢复的最优滤波.
文献[2]提出了一个针对噪声图像恢复的最优形态滤波设计方法,这类最优滤波都是结构映射中含有参数的SV参数形态滤波.为了进一步解决形态滤波的参数优化问题,本文通过对具有 Germ-Grain模型[4]的噪声图像进行分析,利用图像中噪声颗粒相互隔离的特点和SV形态开、闭算子的基本性质[5-8]缩小了最优参数的求解范围.文献[2]通过引入集差距离函数,以平均集差距离最小为标准求解出最优滤波,本文同样利用集差距离函数来构建以恢复误差上界达到最小为标准的最优参数形态滤波的形式,引入度量结构映射直径的方式,采用极大极小估计[9-10]的方法,通过寻找SV最优形态滤波的上、下界,最终实现SV形态滤波的参数优化问题的求解.
1 相关知识
考虑欧氏空间E=Rn或Zn及其幂集P(E),SV结构映射θ(·):E→P(E)的转置定义为:θ′(y)={z∈E|y∈θ(z)},y∈E.其序关系定义为:θ1≤θ2⟺θ1(z)⊆θ2(z),z∈E.若对任意z∈E,结构映射θ(·)都满足:θ′(z)=θ(z),则称θ(·)为对称结构映射.
1.1 SV膨胀和腐蚀
基于结构映射θ(·)的SV膨胀、腐蚀算子σθ(X)、εθ(X):
σθ(X)={z∈E|θ(z)∩X≠∅}=∪{θ′(y)|
y∈X},
εθ(X)={z∈E|θ(z)⊆X}=∩{θ′c(y)|y∈Xc},
它们具有下列性质[8]:
(1)对于集合P(E)中的序列{Xi},i∈Z+(Z+是正整数集合),
(1)
(2)对于结构映射θ1(·)和θ2(·),有:
(2)
(3)对于结构映射θ1(·)和θ2(·),若θ1≤θ2,则:
(3)
1.2 SV形态变换的性质
基于结构映射θ(·)的SV开、闭算子γθ(X)、φθ(X):
γθ(X)=σθ′(εθ(X))=∪{θ(y)|θ(y)⊆X;y∈E},
φθ(X)=εθ′(σθ(X))={z∈E|θ(y)∩X≠∅,∀θ(y)|z∈θ(y)},
它们具有下列性质[8]:
(1)对任意X,Y∈P(E),若X⊆Y,则γθ(X)⊆γθ(Y),φθ(X)⊆φθ(Y)(增性);
(2)γθ(X)⊆X(非扩展性),φθ(X)⊇X(扩展性);

对于集合X1,X2∈P(E),有以下定义和引理:
定义1 设θ(0)(z)是以z为中心的3×3的结构元,且对任意z∈E都有z∈θ(0)(z),若σθ(0)(X1)∩X2=∅,则称集合X1和X2是隔离的.
引理1 若集合X1和X2是隔离的,则有:
γθ(X1∪X2)=γθ(X1)∪γθ(X2).
证明由定义1可知σθ(0)(X1)∩X2≠∅,而X1∩X2⊆σθ(0)(X1)∩X2,故X1∩X2=∅.任取点
ξ∈γθ(X1∪X2),则存在y∈E,使得ξ∈θ(y)⊆
X1∪X2,故有ξ∈γθ(X1)∪γθ(X2), 由此可得:
γθ(X1∪X2)⊆γθ(X1)∪γθ(X2),
又由γθ(·)的增性可知:
γθ(X1∪X2)⊇γθ(X1)∪γθ(X2),
则:
γθ(X1∪X2)=γθ(X1)∪γθ(X2).
定义2[3]对于集合X∈P(E)和结构映射θ(·)∶E→P(E),若γθ(X)=X,则称X是θ-开的;若φθ(X)=X,则称X是θ-闭的.
定义3[3]对于结构映射θ1(·),θ2(·)∶E→P(E),若对任意z∈E都有θ1(z)是θ2-开的,则称结构映射θ1是θ2-开的.
性质1[3](1)X是θ-开的⟺存在集合Y∈P(E),使得:
X=σθ′(Y);
(2)X是θ-闭的⟺存在集合Y∈P(E),使得:
X=εθ′(Y);
(3)若结构映射θ1是θ2-开的,则有:
γ1(X)⊆γ2(X);φ2(X)⊆φ1(X).
若结构映射θ1是θ2-开的,则由性质1进一步可以证得性质2.
性质2 (1)若X∈P(E)是θ1-开的,则X是θ2-开的;
(2)若X∈P(E)是θ1-闭的,则X是θ2-闭的.
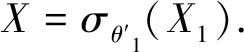
又由θ1是θ2-开的,可得:对任意y∈X1,都存在集合Yy∈P(E),使得:
(4)

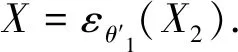
由σθ(X)与εθ(X)的对偶性和(1)式即可得到X是θ2-闭的.
关于SV形态变换的对偶算子,文献[2]中已有详细的阐述,进一步可得到性质3.
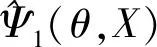
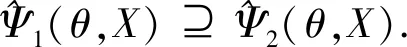
2 两个重要引理
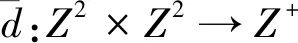
(5)
其中θ1(z)=θ(z),且:
θk(z)=σθ(θk-1(z)),k≥2.
(6)
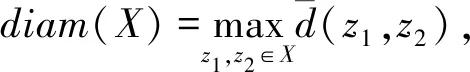
由此所产生的结构映射{θk},具有下列性质4.
性质4 (1)对任意z∈E,都有z∈θk(z),且θk≤θk+1;
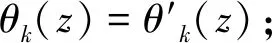
(3)若i≥j,则θi(·)是θj-开的,即θi(z)=
γθj(θi(z));
(4)对于结构映射θ(0)(z)有:
σθk(θ(0)(z))⊇θk(z).
证明(1)因为对任意z∈E都有z∈θ1(z),则由(6)式和σθ(·)的扩展性可得:
z∈θk(z),且θk(z)⊆θk+1(z),即:θk≤θk+1,k∈Z+.
(2)由(2)式可得:
(7)


(3)由(7)式和(2)中结论,以及性质1(1)和性质2(1)即可得到.
(4)(σθk(θ(0)(z)))c={ξ∈E|θ(0)(z)⊆(θk(ξ))c},故任取ξ∈(σθk(θ(0)(z)))c,都有:θ(0)(z)⊆(θk(ξ))c,由z∈θ(0)(z)可知z∈(θk(ξ))c,又由(3)中结论可得ξ∈(θk(z))c,则有(σθk(θ(0)(z)))c⊇(θk(z))c,由此可得:
σθk(θ(0)(z))⊇θk(z).
根据性质4可知(6)式中的结构映射序列{θk}满足文献[2]中的相关条件,其所对应的SV开、闭算子分别为γk(X)和φk(X).
为了研究文献[2]中图像恢复滤波参数优化的求解问题,对于原始图像X受Germ-Grain模型的噪声影响所产生的噪声图像Y作如下假设:
(8)
其中{Ci,n+{xi,n},n=1,2,…}是一系列互相隔离的集合.
令:
Y1=X-N1,Y2=X∪N2,
(9)
由γk(·)和φk(X)的性质,对于(8)式中的噪声颗粒Ni,i=1,2,必存在μ∈Z+,使得:
γk(Ni)=∅,k≥μ,
(10)
且存在υ∈Z+,当υ≥μ时有:
φσθk(θ(0))(Ni)=Ni,0≤k≤υ.
(11)
对于(6)式中的结构映射{θk}和(9)式中的Y1、Y2,可以建立如下两个引理:
引理2 (1)若N2⊆(σθ(0)(X))c∪X,则对任意k≥μ有:γk(Y2)=γk(X);
(2)若N1⊆Xc∪εθ(0)(X),则对任意k≥μ有:φk(Y1)=φk(X).
证明(1)由N2⊆(σθ(0)(X))c∪X,可得:
N2∩Xc⊆((σθ(0)(X))c∪X)∩Xc=
(σθ(0)(X))c∩Xc⊆(σθ(0)(X))c,
(12)
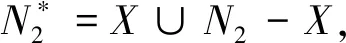
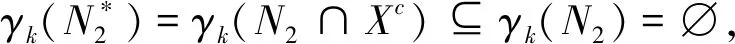
(2)N1⊆Xc∪εθ(0)(X)=Xc∪(σθ(0)(Xc))c,由(1)知:γk(Xc∪N1)=γk(Xc),由γk(·)和φk(·)的对偶性:φk(Y1)=(γk(Xc∪N1))c,则有:φk(Y1)=φk(X),k≥μ.
引理3 (1)若N1⊆Xc∪εθ2k(X),则对任意
0≤k≤υ有:γk(Y1)=γk(X)-N1;
(2)若N2⊆(σθ2k(X))c∪X,则对任意0≤k≤υ有:φk(Y2)=φk(X)∪N2.
证明(1)由性质4(3)和性质1(1)知σθk(θ(0)(z))是θk-开的,由性质1(3)可得φk(Ni)⊆φσθk(θ(0))(Ni),i=1,2.则由(11)式和φk(·)的扩展性可得φk(Ni)=Ni,i=1,2,又由φk(·)与γk(·)的对偶性可得:
(13)
易知γk(X1∩X2)⊆γk(X1)∩γk(X2),故有:
γk(Y1)⊆γk(X)-N1,0≤k≤υ.
(14)
令V(k)=γk(X)-εθ2k(X),0≤k≤υ,任取ξ∈V(k),则有ξ∈γk(X)=γk(γk(X)),且ξ∈(εθ2k(X))c,即存在y∈E,使得:
ξ∈θk(y)⊆γk(X).
(15)
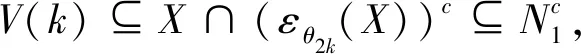
(16)
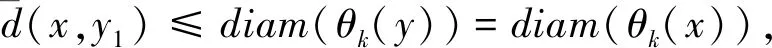
y1∈θ2k(x).
(17)
因为x∈εθ2k(X),则θ2k(x)⊆X,由性质4(3)和γk(·)的增性可知θ2k(x)⊆γk(X).则由(17)式可得y1∈γk(X),所以θk(y)⊆γk(X).故由(16)式可得x∈γk(Y1),于是有γk(X)-N1⊆γk(Y1).又由(14)式可得γk(Y1)=γk(X)-N1,0≤k≤υ.
(2) 因为N2⊆(σθ2k(X))c∪X,则由(1)得γk(Xc-N2)=γk(Xc)-N2,0≤k≤υ,又由φk(·)和γk(·)的对偶性可得φk(Y2)=φk(X)∪N2,0≤k≤υ.
3 SV交替滤波的参数优化


令:
(18)
为此,以下将通过寻找SV最优形态滤波mλ(·)和nλ(·)的上、下界,对滤波参数的最优值进行估计,利用极大极小估计[9]的方法来研究参数λ的最优值,即有下列引理4.
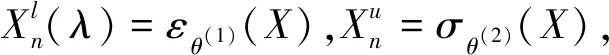
证明由Y=(X-N1)∪N2知Y1⊆Y⊆Y2,由nk(·)的增性可知:
nλ(Y1)⊆nλ(Y)⊆nλ(Y2),
(19)
令V1(λ)=Xc∪εθ2λ(X),则由引理3(1)可知:若
N1⊆V1(λ),0≤λ≤υ,则有:
γλ(Y1)=γλ(X)-N1,
(20)
令V2(λ)=(γλ(X))c∪εθ(0)(γλ(X)),则由引理2(2)知:若N1⊆V2(λ),λ≥μ,则有:
φλ(γλ(X)-N1)=φλ(γλ(X))=nλ(X),
(21)

εσθ2λ(θ(0))(X)⊆εθ(0)(γλ(X)).由γλ(·)的非扩展性得Xc⊆(γλ(X))c,即有V(λ)⊆V2(λ).由(20)式和(21)式可知,若N1⊆V(λ)⊆Vi(λ),i=1,2,μ≤λ≤υ,则有:
nλ(Y1)=φλ(γλ(Y1))=φλ(γλ(X)-N1)=nλ(X).
(22)

∪{Ci,n+xi,n|(Ci,n+xi,n)∩(V(λ))c≠∅}.
(23)


(24)
nλ(Y2)=φλγλ(Y2)=φλγλ(X)=nλ(X),λ≥μ,
(25)
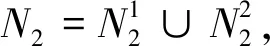
(26)
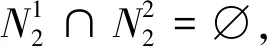
(27)
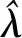

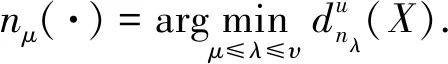
证明(1)由σθ(·)和φλ(·)的扩展性,以及εθ(·)和γλ(·)的非扩展性有:

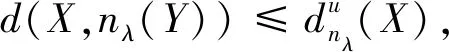
(2)由性质1(3)和性质4(3)可知:
γk(X)⊆γk-1(X),φk(X)⊇φk-1(X),
(28)


类似于引理4和定理1,对于最优滤波mλ(·)可得到如下引理5和定理2.
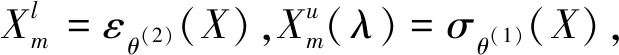
μ≤λ≤υ.
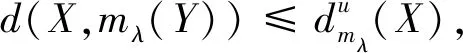

4 SV交替惯序滤波的参数优化

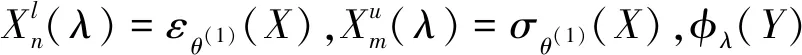
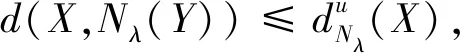
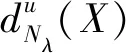
5 结语
在SV最优形态滤波的结构映射序列中选取条件更好的结构映射,利用图像中的噪声颗粒相互隔离的特点和SV形态开、闭的基本性质缩小最优参数的求解范围,通过寻找SV最优形态滤波的上、下界对滤波参数的最优值进行估计,最终使得形态滤波的参数优化问题得以解决.后续将对所推证的图像恢复滤波的最优参数进行实验验证,以完善此研究工作.
- 中南民族大学学报(自然科学版)的其它文章
- 基于FS-YOLOv3及多尺度特征融合的棉布瑕疵检测
- 基于显著性检测和Grabcut算法的茶叶嫩芽图像分割
- 基于RSU协作的V-NDN数据转发方法研究
- 子句级别的自注意力机制的情感原因抽取模型
- Gallium-incorporated zinc oxide films deposited by magnetron sputtering and its microstructural properties
- Comparison of different methods for quantification of proanthocyanidins from grape seeds

