DDA 圆弧插补算法改进研究

游达章，谈太振，张业鹏，刘 攀

（湖北工业大学 机械工程学院 湖北省现代制造质量工程重点实验室，湖北 武汉 430068）

0 引 言

插补算法是整个数控系统的核心。数控机床加工曲线时，对其起点和终点之间，按照一定的方法用折线轨迹逼近、拟合所要加工的曲线[1]，并计算出中间点位置的坐标值，给出相应的位移量，这就是插补。插补运算具有实时性，每个插补中间点的计算精度影响系统的控制精度，中间点的计算速度又影响着系统的控制速度。

数字积分法（DDA）具有逻辑能力强、运算速度快、易实现多标联动等特点。现阶段圆弧插补算法在应用上存在着误差较大和溢出脉冲不均匀等缺点。文献[2]通过非对称累加器赋值，使得轴上脉冲分配更均匀，同时减少了插补次数，插补算法难度不变。但是通过累加器改变初值的方式造成程序段进给速度不一致，影响加工表面质量。

文献[3]基于数字积分法和时间分割混合，采用可控的插补周期进行时间分割，满足DDA 累加中对进给速度的要求，从而消除了插补段之间的零头距离，让进给速度更平滑。但是必须要求CNC 完成一次插补所需的最小周期不长于插补周期[4]，对硬件要求高。区别于传统时间分割法，粗插补利用插补周期及进给速度计算步长完成分割，本文通过控制弓高误差，利用固定长度弦和迭代矩阵计算插补点的方式对DDA 算法进行改进，提高了插补精度及插补效率，并提出一种基于最小二乘法的评价方法对改进后的算法做出评价。

1 基于时间分割法的DDA 算法分析

基于时间分割法的DDA 圆弧算法思想是在误差范围内将圆弧转化为一组直线来逼近，即需要计算出每个插补周期的坐标增量值[5]。对于圆弧的逼近，目前数控系统使用有切线法、弦线法和扩展DDA 法（割线）三种方式。

切线法和弦线法的逼近方式都属于一阶DDA，在计算三角函数时，因为一个插补周期转动角度θ 较小，利用泰勒展开：

取一阶近似计算，造成进给速度小于指令速度，每次插补的轮廓步长发生误差积累。基于时间分割法的扩展DDA 法是目前精度最好的方式，它采用二阶运算，只需有限次加法、减法、乘法运算，速度较高[4]。如图1所示，做逆圆弧插补时，设一个插补周期进给步长为l，其径向误差δ=Ri-R，插补半径为：

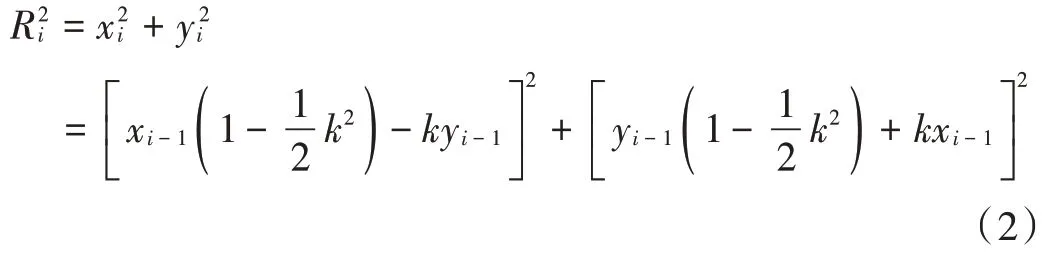
化简，得：

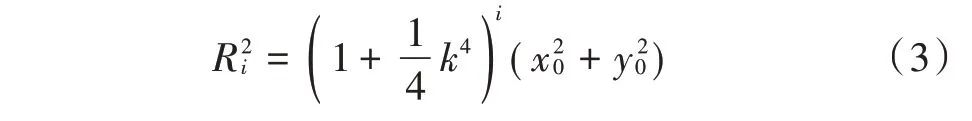
(x0,y0)为圆弧起点，在圆弧上则有：

式中所以径向误差δ≠0。由此可知，插补点如果不在圆弧上，就存在径向误差[4]，在迭代插补时，将形成较大的累计误差，圆弧插补径向误差分析如图1所示。

图1 圆弧插补径向误差分析

2 圆弧插补算法改进

由第1 节圆弧插补误差分析可知，基于时间分割法的DDA 算法常用的三种方式存在精度误差。因此，本文考虑对算法进行改进。与传统时间分割法不同，改进算法是在插补前通过缩放圆弧形成允许误差带[6]，控制弓高误差，利用连续的弦线拟合圆弧，最后通过DDA 完成各段直线插补拟合圆弧。

不失一般性，设起点、终点坐标为(xs,ys)，(xe,ye)，圆心坐标为(x0,y0)，起点、终点相对原点偏置如下：

起点、终点向量扫过的夹角为τ，设起点、终点向量斜率存在，且为ks，ke，则有：

在第一象限逆圆弧插补中，设当前位置为起始位置C(xs,ys)，下一插补点的坐标为B(x1,y1)，设置允许误差，切线对应圆心角，其中，δ 为弓高误差，R为圆弧半径，分割圆弧如图2 所示。

图2 通过弓高误差控制分割圆弧

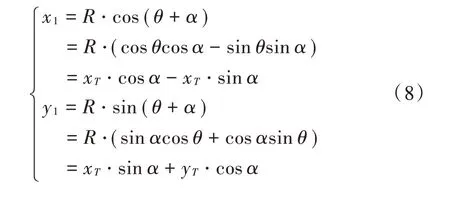
转换为旋转矩阵：

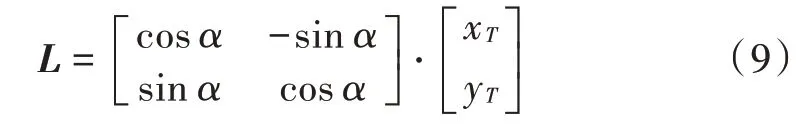
式中xT，yT为迭代坐标，初始值为xs，ys，矩阵计算的结果L 为下一插补点坐标，并重新代入xT，yT中完成式（9）迭代计算。如图3 所示，每计算一次插补点，剩余夹角为τ-α。当剩余夹角β =α，迭代计算下一插补点坐标；当β ＜α 时，不再计算，弦线由当前点N 直接连接至终点B。有了插补点坐标，可通过相邻点连接的弦完成圆弧逼近[7]，再通过DDA 直线插补对每段逼近直线插补。终点判别过程如图3 所示。

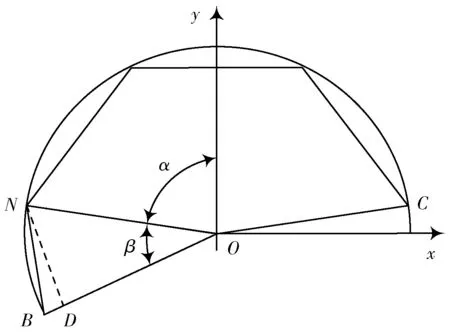
图3 终点判别

3 圆弧拟合均差数学模型

同直线插补一样，圆弧插补由x,y 方向移动若干脉冲当量来拟合圆弧轨迹[8]。不失一般性地，设最小二乘圆圆心为(xc,yc)，半径为R，最小二乘法拟合要求距离平方和最小[9]。由最小二乘圆公式可知：

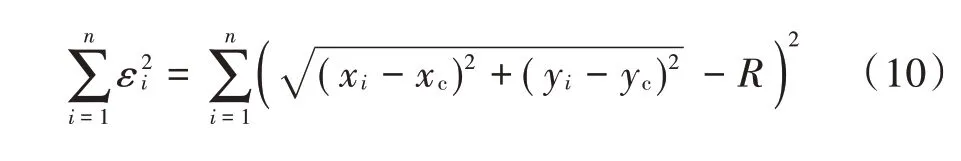
式中（xi，yi）为离散点的坐标，即求解最小二乘圆圆心xc，yc和半径R，使得最小。由于最小二乘圆计算方法无解析解，因此可对最小二乘法进行一定的近似[9]，采用近似函数进行求解，为方便运算，设函数：

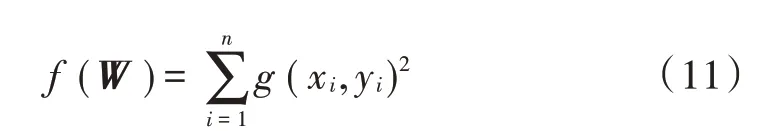
式中W =[xcycR]T。

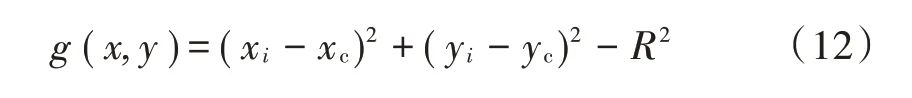
对f (W )求偏导，并令其为0，可得：

通过将xc，yc由uc，vc替换，修改坐标原点位置，由于可得：

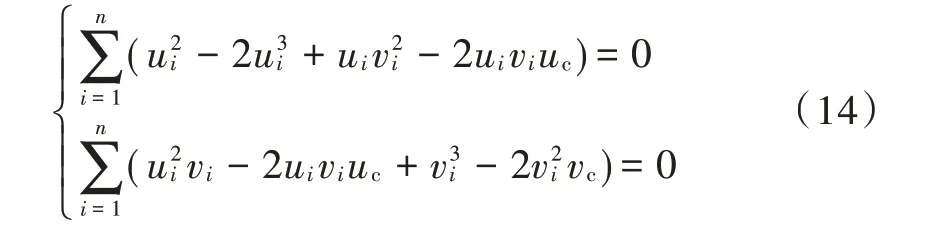
综上，可得：

至此，可得出最小二乘圆圆心：

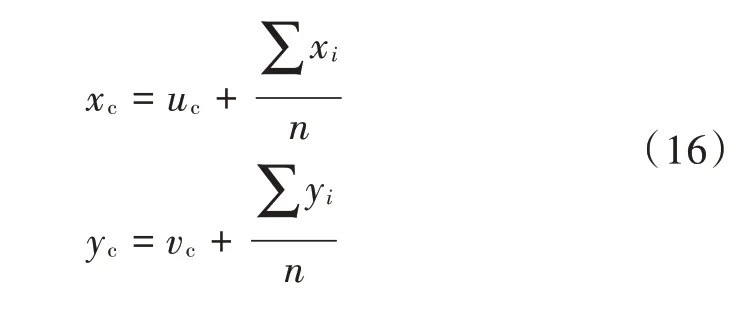
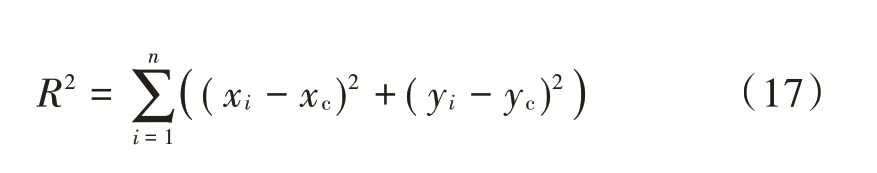
由以上分析可知，最小二乘圆的圆心和半径是可解、存在的，这说明基于最小二乘圆近似算法可以作为圆弧插补的快速评价方法。

4 比较分析

通过圆弧插补均差数学模型，建立最小二乘圆拟合，利用Matlab 对切线法、弦线法、扩展DDA、改进DDA算法进行仿真，基于这种快速评价方法进行比较分析。仿真结果如图4 所示。

图4 中实点表示插补点分布，虚线表示最小二乘圆轨迹，实线为理想条件下要求的插补轨迹，由最小二乘圆拟合轨迹，显然可得出改进后的DDA 算法能够更好拟合理论圆弧。最小二乘圆拟合情况如表1 所示。

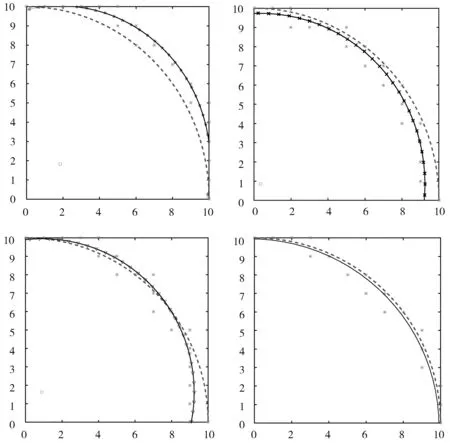
图4 算法仿真

分别计算切线法、弦线法、扩展DDA 以及改进DDA算法插补点最小二乘圆，其中，改进DDA 算法误差控制为δ=0.5，并求出插补点距离最小二乘圆距离平方和通过最小二乘圆实际求取的半径精度、最大径向误差对4 种插补算法进行对比，结果如表2 所示。

表2 插补情况对比

由表2 可得出，传统圆弧插补最大误差可能超过1 个脉冲当量，而改进插补误差则总是控制在1 个脉冲当量内，故改进后DDA 算法最大误差不超过1+δ，且改进后的DDA 算法最小二乘拟合精度相对于已有的传统DDA 算法提高了约20%，最大径向误差更小，运行时间也更短。

5 结 语

通过本文的分析，经过改进后的DDA 算法用迭代矩阵计算插补点、弦线分割圆弧的方式逼近圆弧，可靠地提高了插补精度，在运行时间上也得到很大的提升。同时，也验证了基于圆弧插补均差数学模型的最小二乘圆评价插补精度具有一定的可行性。