基于经验模态分解的粒子图像测速流场重构研究

王晓宇,贺静,柯汉兵,林梅

(1.西安交通大学能源与动力工程学院,710049,西安;2.武汉第二船舶设计研究所,430205,武汉)

粒子图像测速(PIV)技术是一种诞生于20世纪80年代的无扰动流场测试技术,它克服了传统接触式流场测量中单点测量的局限性,可以对存在变化流速及各类涡结构的复杂流动实现全流场瞬时非接触测量[1-2]。在PIV流场图像后处理中常采用光学杨氏条纹法、自相关法或互相关法,逐点处理PIV图像,从而获得流场速度数据[3-4]。由于在实验中可能存在示踪粒子分布不均匀、PIV图像变形或扭曲、PIV图像背景噪声、成像系统变形等因素,获得的流速数据中会存在干扰正常流场分析的错误数据。当错误数据造成的误差超过2%时,便会影响正常的流场分析研判[5]。

针对PIV流场数据中错误数据的消除方法,国内诸多学者都进行了相关研究。王平让总结了错误数据产生的原因,并从PIV图像滤波处理的角度提出了消除错误数据的方法[6]。王灿星等建立了基于互相关技术的连续PIV图像之间的粒子对应方法,提出了识别错误数据的方法和消除准则[7]。高琪等基于速度场的本征正交分解后处理技术,通过迭代方法有效地实现了错误数据的识别与修复[8]。吴龙华等在对人脑判别PIV错误数据方式进行模拟的基础上,建立了可以进行准确错误数据识别的多证据推理Hopfield神经网络模型[9]。王晋军等引入不可压缩连续性方程对PIV测得的流场数据进行后处理,使得修正后的流场严格满足差分形式的连续性方程,实现了流场数据的准确修正[10]。阮晓东等采用Delaunay网格技术建立了基于流体连续性假设的自动检测PIV数据中错误数据的算法,实现了错误数据的识别与替换[11]。张工利用Visual C++开发了通用的PIV图像后处理软件,实现了PIV图像的增强等功能,可以从PIV图像中消除部分错误数据[12]。王元等广泛研究了各类提高流场测量及数据后处理精度的粒子追踪算法,减少了错误数据的产生[13-16]。上述方法对PIV流场数据中错误数据的剔除和修正都有较好的效果,但也存在处理流程复杂、效率不高、引入非物理偏差等不足。

本研究提出了一种基于经验模态分解(EMD)的PIV流场数据后处理方法,将数据分解得到的波形异常的本征模态分量(IMF)进行滤波处理并与其余波形平滑的正常本征模态分量进行反向叠加,重构流场数据,使错误数据得到有效剔除。当分解得到的本征模态分量较多且错误数据集中在某一个本征模态分量时,直接将与原始流场数据相关的本征模态分量反向叠加重构流场数据,摒弃不相关的本征模态分量,实现错误数据的直接剔除。本方法已经在多个模拟或实验获取的变化较为缓和的平稳流场数据处理中得到了良好的使用,本文利用该方法对2个典型的人为添加错误矢量的模拟标准流场进行数据处理,同时对某实验的原始流场数据进行修正,以上述3个流场为例,说明并验证该方法的可行性。

1 基于经验模态分解的流场数据重构原理

1.1 经验模态分解概述

经验模态分解是Huang等于1998年提出的一种无需基函数的自适应性信号数据处理新方法,在各工程领域得到了广泛、高效的应用[17-18]。该方法利用数据自身的尺度特征进行数据分解,特别适用于非平稳、非线性数据的平稳化处理。经验模态分解处理信号的基本步骤如下。

(1)确定随机信号x(t)在整个时间尺度上的所有极大值点和极小值点,并用三次样条差值曲线分别连结所有极大值点和极小值点,形成上包络线a(t)和下包络线b(t),求取上、下包络线的平均值

(1)

(2)求取原始随机信号x(t)与m(t)之间的差值

h(t)=x(t)-m(t)

(2)

(3)如果h(t)的极值点与过零点的个数最多相差一个且h(t)的上、下包络线的均值为0,则h(t)为第一个本征模态分量c1。求取x(t)与c1的差值

r(t)=x(t)-c1

(3)

将r(t)视为最新的随机信号,重新开始上述分解过程(1)～(3)求取剩余的本征模态分量,直至r(t)变为单调信号。如果h(t)不能满足上述条件,则将h(t)视为最新的随机信号,重新开始上述分解过程(1)～(3)。

关于经验模态分解更加具体的数学化描述及证明过程请参见文献[19-20]。经过经验模态分解后,一组数据可以被分解为若干个表征不同数据尺度和数据特征的本征模态分量,它们是组成原始信号的不同尺度的一系列分量,是对原始信号特征的一系列表达。理论上连续的两个本征模态分量的标准差在0.2～0.3之间时,则分解得到的本征模态分量既能满足线性条件,稳定性良好,又能够较好地反映原始随机信号的性质。经验模态分解具有正交性和完备性的特征,因此将分解得到的本征模态分量反向叠加即可得到原始数据。在处理现代流动测试技术所获得的流场数据时,数据量的大小并不会直接影响所分解出的本征模态分量数量,而原始流场的复杂程度则对本征模态分量的数量影响较大。原始数据经过经验模态分解后一般可以得到5～15个本征模态分量,其中本征模态分量在5～10个时可以认为较少,超过10个时可以认为分解得到的本征模态分量较多。

1.2 相关系数概述

在数据处理中常用相关系数来表征两组数据之间的相关程度,在本研究中通过求解不同的本征模态分量与原始流场数据的相关系数,可以判断该分量与原始流场数据的相关程度。相关系数的划分并没有固定的标准,而是根据所处理数据的具体特征来决定的。表1所示的是一种相关性的划分方式,本研究根据这种相关系数大小的划分方式将本征模态分量与原始流场数据的关系归类为不相关、微相关、实相关、高度相关4类,其中微相关、实相关、高度相关统称为相关。

表1 相关性划分

1.3 流场数据处理流程

图1是本研究所提出的基于经验模态分解的PIV流场数据后处理方法流程图,其中实线表示的流程是通用方法,虚线表示的流程是在原始流场较为复杂、原始流场数据经过经验模态分解后得到的本征模态分量较多且错误数据集中在某一个本征模态分量时对通用方法的一种简化。

图1 基于EMD的PIV流场数据后处理流程图

错误数据在数值大小和方向上与正确数据有明显的差异,在原始流场数据没有经过经验模态分解时,错误数据掺杂在正确数据中难以识别。当用经验模态分解将原始流场数据分解为若干个本征模态分量时,错误数据就会造成本征模态分量曲线出现明显的局部不平滑。由于错误数据造成本征模态分量曲线局部的不平滑十分明显,因此常用的滤波方法就可以将错误数据点在本征模态分量中滤除而不误删正确数据。根据经验模态分解的正交性和完备性,波形异常的本征模态分量经滤波处理后与波形平滑正常的本征模态分量反向叠加就可以重构剔除了错误数据的流场数据。上述的原始流场数据处理思路可表示为图1中实线所示的流程。

原始流场数据经过经验模态分解后得到的本征模态分量越多,每个本征模态分量携带的原始流场数据就越少,所占原始流场数据的比例就越小。在有些实验中,粒子图像测速技术所获得的流场数据相对比较复杂且错误数据比较明显,这时分解得到的本征模态分量较多且错误数据会集中在某一个本征模态分量。掺杂了错误数据的本征模态分量波形异常且与原始流场数据的相关性较低(呈不相关),因此在该流程中可以通过求解各本征模态分量与原始流场数据的相关性大小来判断错误数据所在的本征模态分量。为了提高处理速度和效率,可以按照图1中虚线所示的处理流程,省略相关性低(呈不相关)的本征模态分量的滤波过程,直接将该分量删除并将其余相关性较高的本征模态分量反向叠加直接重构流场数据。随着错误数据的删除,也会损失该本征模态分量中的正确数据,但在分解得到的本征模态分量较多的情况下,损失的小部分正确数据不会对整体流场数据造成明显的影响,流场的特性仍然可以清楚地表达。

2 算例验证与应用分析

2.1 模拟流场中的验证与分析

图2是用计算机模拟的流速为1 m/s的单向均匀流场,在4 000个原始流场数据中加入了明显的错误数据,人为添加的误差约为1.7%,因此速度矢量场中出现了数值大小和方向明显错误的速度矢量。图3是原始流场数据按图1中实线流程处理后得到的速度矢量场。图4和图5是对该原始流场x、y方向全部的4 000个流场数据进行经验模态分解后得到的本征模态分量,分别为6个和8个,不符合使用简化流程的要求,因此采用的是通用方法。由图可知x、y方向的错误数据都集中在了第1个本征模态分量中,因此该本征模态分量的曲线中出现了不平滑的跳变点,也正是错误数据存在的位置。对x、y方向上错误数据集中的第1个本征模态分量进行滤波处理,即可把错误数据存在的跳变点滤除而不误删正确数据。将x、y方向上滤波处理后的第1个本征模态分量与其他本征模态分量反向叠加,即可重构流场数据。图2与图3对比表明,实线表示的处理流程能有效实现该单向均匀流场错误数据的剔除和速度矢量场的修正,修正并重构后的流场数据与正确流场数据的误差约为0.002%。

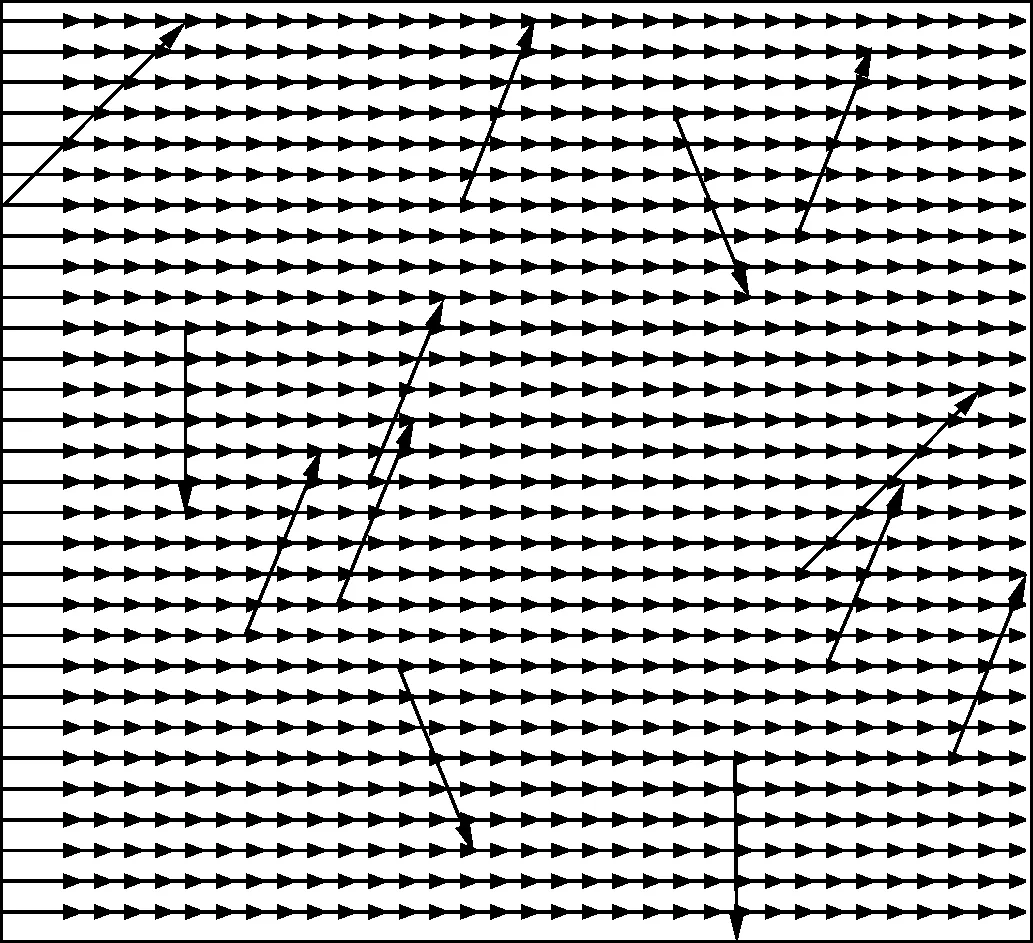
图2 原始单向流场数据得到的速度矢量场

图3 处理后的单向流场数据得到的速度矢量场

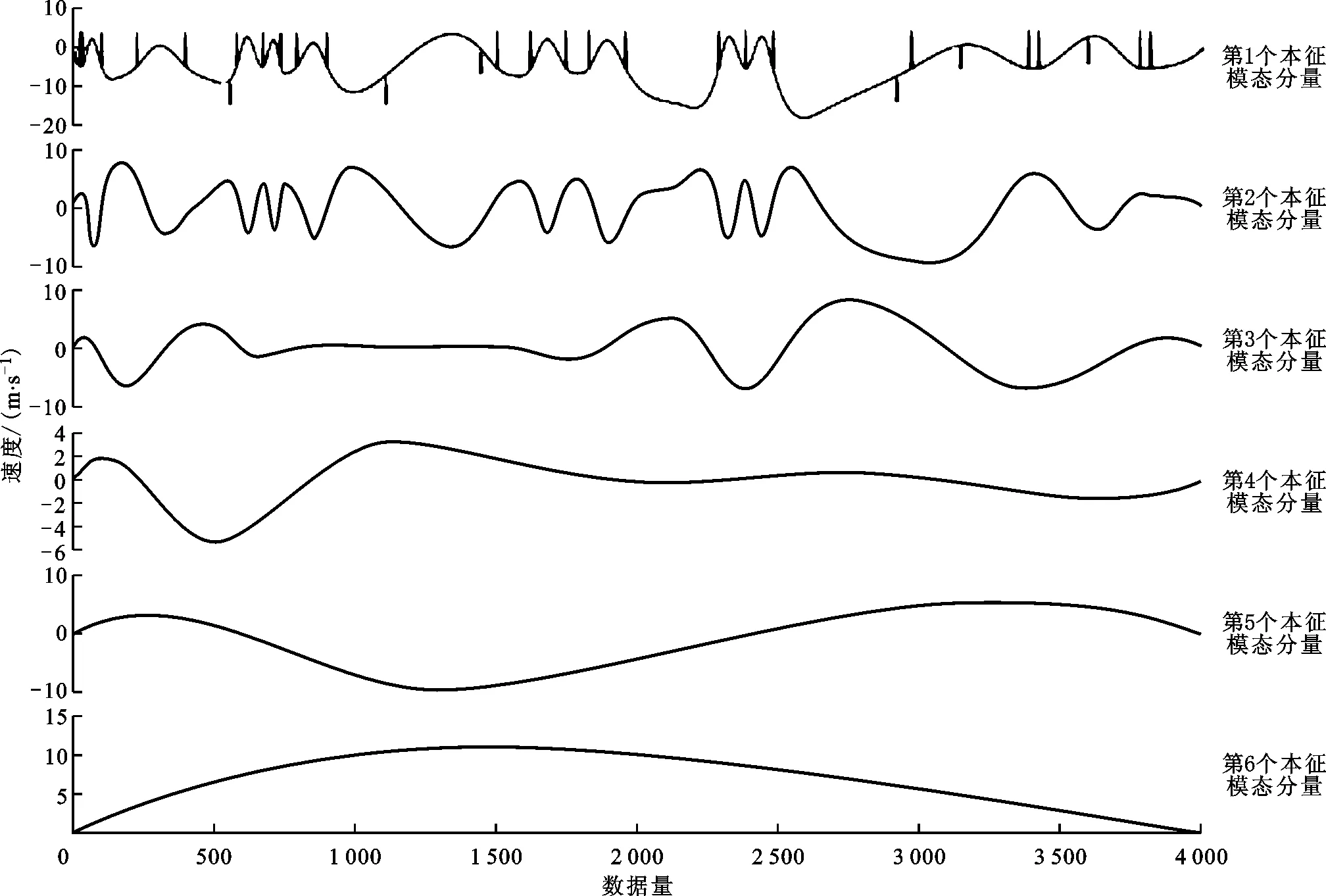
图4 原始单向流场x方向数据的本征模态分量

图5 原始单向流场y方向数据的本征模态分量

为了验证所提出的方法在处理相对复杂的流场数据时的有效性,本研究模拟了速度大小不定的单向旋转流场,并在原始流场数据中加入了一些明显的错误数据,人为添加的误差约为3.3%。图6和图7是对该原始流场x、y方向的流场数据进行经验模态分解后得到的本征模态分量与原始流场数据的相关系数,本征模态分量的数量和特点符合上文提出的虚线表示的简化处理流程的要求,因此处理该流场数据时采用的是简化流程。图8和图9分别是由原始流场数据和按图1中虚线表示的简化流程处理后的流场数据得到的速度矢量场。对比表明,图1中虚线表示的简化处理流程能够有效地实现该速度大小不定的单向旋转流场中错误数据的剔除和速度矢量场的修正,修正并重构后的流场数据与正确流场数据的误差约为0.18%。

图6 旋转流场x方向流场数据的各本征模态分量与原始流场数据的相关系数

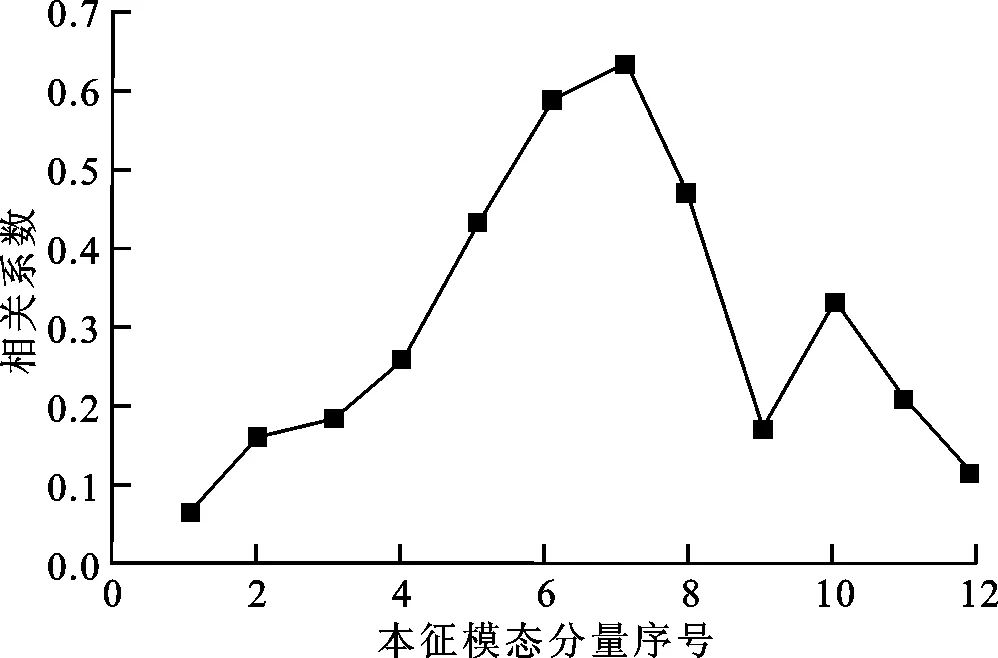
图7 旋转流场y方向流场数据的各本征模态分量与原始流场数据的相关系数

图8 原始旋转流场数据得到的速度矢量场

图9 处理后的旋转流场数据得到的速度矢量场

2.2 实验流场中的应用与分析

为了验证本文所提出的基于经验模态分解的PIV流场数据后处理方法在实验流场数据处理中的准确性与实用性,本研究对低速风洞中某一T型通道的PIV流场原始数据进行了处理与分析。关于该T型通道PIV流动测试实验的具体细节请参见文献[21-22]。

正如上文所述,实验流场的复杂性一般相对较高,流场数据经过经验模态分解之后得到的本征模态分量较多。该实验流场x、y方向的原始流场数据经过经验模态分解之后分别得到了10个本征模态分量和12个本征模态分量,可以用图1中的简化流程进行数据处理。图10和图11分别表示了x方向流场数据、y方向流场数据的本征模态分量与原始流场数据之间的相关程度。由图可知,x方向流场数据的第1个本征模态分量和y方向流场数据的第6个本征模态分量与原始流场数据的整体相关性很小(呈不相关),是错误数据集中的具体表现。该流场数据可以按照图1中虚线表示的流程进行处理,直接删除这两个本征模态分量,将x、y方向上剩余的9个、11个本征模态分量反向叠加重构流场数据。图12、图13分别表示了该流场数据处理前后的速度矢量场,可知原始流场数据中位于速度矢量场上部的错误数据(图12中区域1)得到了准确的剔除,一些明显的错误矢量得到了有效的消除,速度矢量场更加平滑,品质得到了显著改善,速度矢量场上部的流动特征(图13中区域1＇)也更加趋近于文献[22]报道的各工况下的真实流动情况,但在个别不存在错误矢量的区域出现了流场特征的轻微变化。这是随着简化流程中呈不相关的本征模态分量的直接删除,造成少部分正确数据损失所导致的。如果对局部流场特性的准确性要求较高,可以不采用简化流程,而采用相对较为烦琐的通用方法来进行处理。

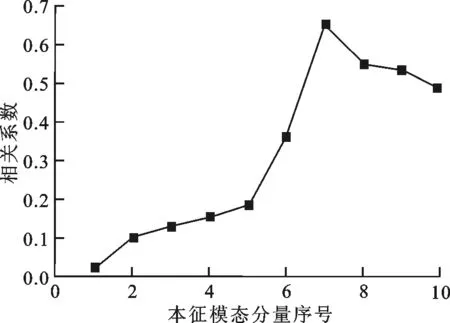
图10 实验流场x方向流场数据的各本征模态分量与原始流场数据的相关系数

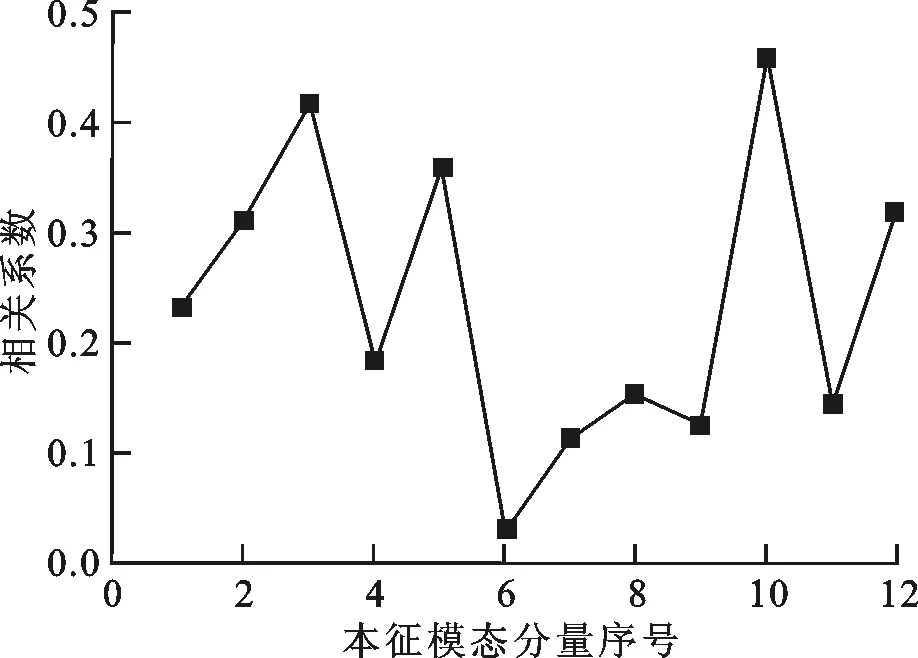
图11 实验流场y方向流场数据的各本征模态分量与原始流场数据的相关系数

图12 原始实验流场数据得到的速度矢量场

图13 处理后的实验流场数据得到的速度矢量场

3 结 论

本研究提出了一种基于经验模态分解的PIV流场数据后处理方法,对存在错误数据的本征模态分量进行滤波处理或直接删除,将其余本征模态分量反向叠加,实现了错误数据的剔除与流场数据的重构。利用该方法处理了计算机模拟流场和某实验流场的原始数据,结果表明错误数据得到了有效剔除,重构的流场数据可更加真实地反映流场特征。

目前任何一种PIV流场数据后处理方法都不能完全将错误数据剔除而不影响正确数据,本研究所提出的方法也是如此,但本方法具备以下两个优点:首先,该方法最大限度地从原始流场数据中剔除了错误数据,并非通过各类算法在计算时“避开”错误数据,具备处理的彻底性;其次,该方法简单易行,没有复杂的错误数据识别流程与标准,可以快捷简便地提高流场分析的准确性。在PIV技术中,错误数据超过2%就已经会影响流场分析,证明实验中存在的误差太大,此时解决误差大的最好办法是重新进行实验,而不是消除已有的错误数据。就这一点而言,本方法对误差在2%以内的流场数据是有效的,但本方法也有自身的缺点,当所处理的流场变化非常剧烈、杂乱(例如射流撞击壁面)时,本方法容易把部分真实反映流场的数据视为错误数据,因此本方法只适用于处理变化较为缓和的平稳流场。

受该方法的启发,也可以将原始的PIV图像视为一个二维数组,利用经验模态分解的方法通过上述流程来对其进行处理。这时处理的对象是PIV原始粒子图像,各个本征模态分量也是以图像或数组的形式来呈现的,最终通过本征模态分量的反向叠加得到处理后的PIV图像,并从中提取流场数据。此外,本方法在三维流场数据中的应用及可行性还有待验证,在接下来的研究工作中,上述两部分内容将是研究的重点。