非对称声学超材料的各向异性反射特性及等效参数

徐宜才,吴九汇

(西安交通大学机械工程学院,710049,西安)

声学超材料是具有亚波长尺寸特征的人工复合结构,其主要的研究目标是设计具有新颖声学特性的人工超结构[1-6]。最近,非对称结构的各向异性反射特性成为研究热点,该特性是由于非对称结构具有Willis耦合效应。弹性波的Willis耦合是指应力与速度或者动量与应变的耦合[7]。Willis首次在不均匀弹性介质的动态响应中描述了这种耦合特性,从此研究者把这种耦合关系称为Willis耦合[7]。Muhlestein等推导了假设Willis材料具有互易性、被动性和因果性时,材料特性所受到的约束条件[7]。Xiang等证明了非均匀预应力材料的线弹性行为可以用Willis方程来描述[8]。Liu等在实验中实现了弯曲波的Willis耦合,他们利用悬臂梁的弯曲共振证明了Willis耦合引起非对称的反射幅值和反射相位[9]。Liu等利用被动宇称-时间对称超材料晶体在二维空间实现了单向波矢量的操纵[10]。被动宇称-时间对称系统的不对称反射特性类似于Willis耦合形成的各向异性。Merkel等将声Willis耦合与宇称-时间对称系统的特性统一在同一框架下,表明一个简并点在任何情况下都具有显著的散射不对称性并伴随着声波的单向零反射[11]。

许多研究者提出了不同的设计方案来实现声学超材料的Willis耦合[12-15]。Muhlestein等提出了一维非对称声学系统,并用实验和理论证明了非对称系统的局域行为产生了非对称的等效参数,他们还提出了改进的反演法来计算非对称系统的统一等效参数,然而反演法默认求解的模型是质心对称结构,并不适用于几何非对称型声学超材料[12]。此外Willis耦合还产生各向异性反射特性,而Muhlestein等没有研究这部分内容。Ma等研究了双层非对称声学超材料的声学特性,并利用改进的反演法计算了考虑Willis耦合的等效参数[13]。然而Ma等没有研究材料损耗对声学特性的影响,对各向异性反射特性的形成机理也揭示的不清楚。Quan等推导了声散射体Willis耦合的一般边界,表明在适当设计的散射体中可以达到这些边界,并为最大各向异性内含物的实现勾勒出一个系统的场所[14]。Craig等利用反转对称破坏的声光栅系统地实现了非对称波传播时压力场和速度场之间任意给定的各向异性耦合[15]。打破非对称性不仅会产生各向异性的反射特性,还会产生各向异性的透射特性。Li等利用梯度超表面实现了声波的各向异性折射,通过局部控制元胞的各向异性响应来确保对折射波的完全控制[16]。Li等还设计了3个折射超表面,可以将法向入射的平面波在透射侧分别重新定向到60°、70°和80°方向[16]。

为揭示各向异性反射特性的形成机理,本文研究了材料非对称、几何非对称和共振非对称3种结构的声学特性,通过仿真和实验对比分析了材料损耗对声学特性的影响。提出了直接法来求解几何非对称结构的等效参数,进一步提出了改进的直接法来求解考虑Willis耦合的统一等效参数,并利用透射幅值和被动材料的要求验证了求解的等效参数的正确性。

1 材料非对称型声学超材料

1.1 几何模型

典型的双层薄板声学超材料如图1所示,该图是三维结构在rz平面的截面,该结构是由两层圆形薄板耦合一层空气组成[13]。当两层薄板的材料和尺寸完全相同时,该结构在z轴方向是一个完全对称结构。双层薄板声学超材料的几何参数包括:薄板的半径r0为20 mm,薄板的厚度t为0.2 mm,空气层厚度d为10 mm。当上层薄板选用聚对苯二甲酸乙二醇酯材料(PET),下层薄板采用尼龙材料,该模型是一个材料非对称型声学超材料,对应的材料参数见表1。

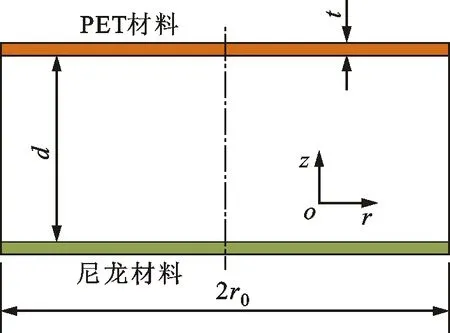
图1 材料非对称型声学超材料

表1 非对称声学超材料的材料参数

1.2 各向异性的反射特性

为探究非对称声学超材料两侧声学特性的差异,利用有限元软件Comsol Multiphysic分别计算了平面波从结构两侧法向入射的结果。计算时采用二维轴对称模型,圆形薄板的外边界设置为固定边界。通过设置材料的各向同性损耗因子,还研究了材料损耗对声学特性的影响。

图2是材料非对称型声学超材料无损耗声学特性的仿真结果。平面波从PET薄板一侧法向入射得到的声学特性记为P侧的声学特性,平面波从尼龙薄板一侧法向入射得到的声学特性记为N侧的声学特性。两侧的反射幅值|R|和透射幅值|T|完全相同,两侧的反射相位arg(R)完全不同。各向异性的反射特性具体是:在透射幅值的第1个峰值处,两侧的反射相位都发生突变,P侧的相位突变为2π,而N侧的相位突变小于2π;在透射幅值的第2个峰值处,只有N侧的反射相位发生2π的突变;在透射幅值的第3个峰值处,只有P侧的反射相位发生2π的突变。上述分析表明材料非对称型声学超材料在无材料损耗下具有各向异性的反射相位。

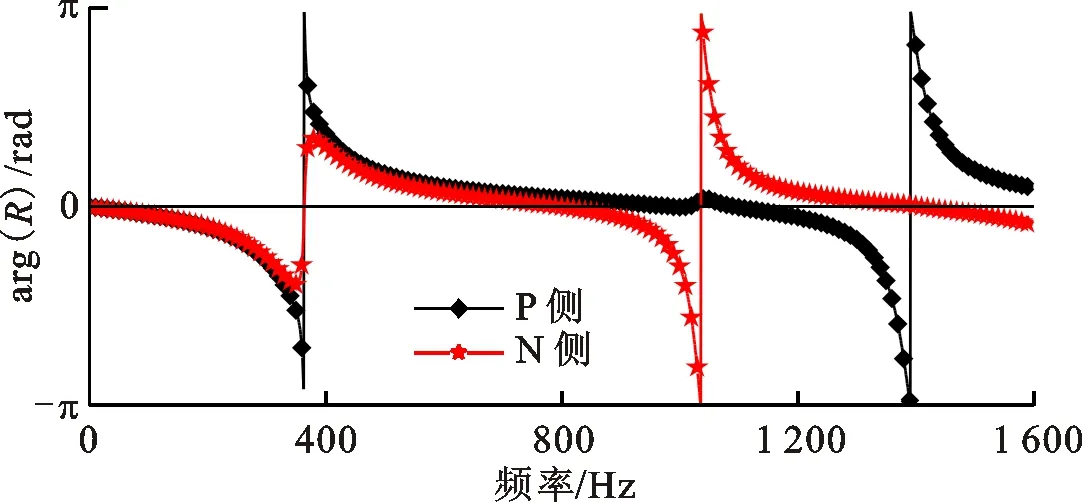
(b)反射相位图2 材料非对称型声学超材料无损耗的声学特性的仿真结果

将PET材料和尼龙材料的各向同性损耗因子分别设置为0.115和0.15,材料非对称型声学超材料有损耗的声学特性的仿真结果如图3所示。两侧的透射幅值完全相同,两侧的反射幅值和反射相位完全不同。两侧的透射幅值有无损耗下始终是相同的,这是由于本文研究的非对称声学超材料都是线性时不变系统,具有互易的传输特性。各向异性的反射特性具体是:在透射幅值的第1个峰值处,两侧的反射幅值都出现谷值,但是P侧的反射幅值小于N侧的反射幅值;两侧的反射相位都发生突变,P侧的相位突变大于N侧的相位突变,受材料损耗的影响,P侧的相位突变也小于2π。在透射幅值的第2个峰值处,两侧的反射幅值都出现谷值,但是N侧的反射幅值远小于P侧的反射幅值;只有N侧的反射相位发生突变,受材料损耗的影响,相位突变小于2π。在透射幅值的第3个峰值处,只有P侧的反射幅值出现谷值;也只有P侧的反射相位发生突变,受材料损耗的影响,相位突变小于2π。对比图2可知,材料损耗产生了各向异性的反射幅值并且减小了反射相位的突变幅值。考虑材料损耗不仅能获得各向异性的反射幅值,还可获得各向异性的吸声特性。在透射幅值的第2个峰值处,N侧的反射幅值出现谷值,该处的透射幅值也较小,经计算该处的吸声系数为0.908,呈现良好的吸声特性。在透射幅值的第3个峰值处,P侧的反射幅值具有较小的谷值,该处的透射幅值也较小,经计算该侧的吸声系数为0.985,呈现完美的吸声特性[17]。上述计算结果表明材料非对称型声学超材料具有各向异性的反射相位,考虑材料损耗下还具有各向异性的反射幅值。

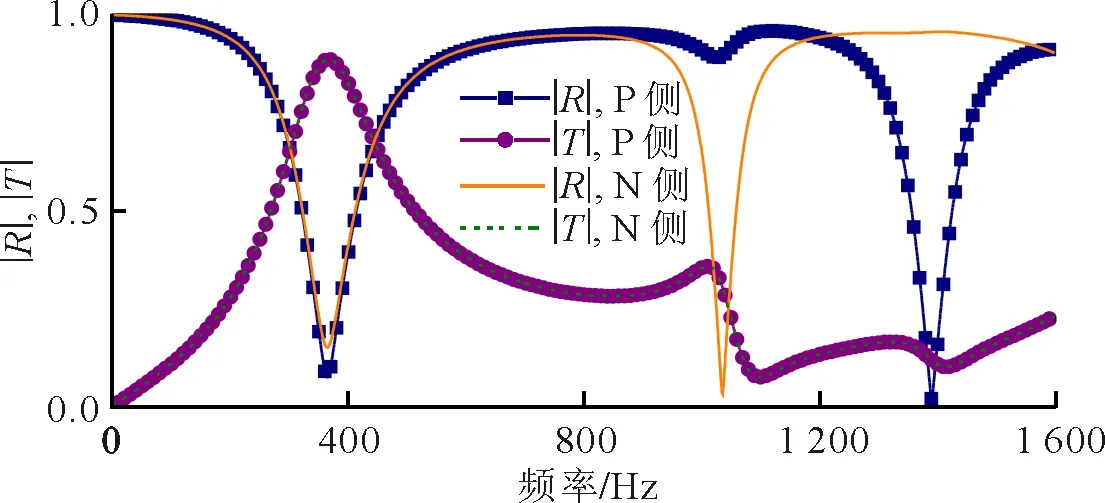
(a)反射和透射幅值

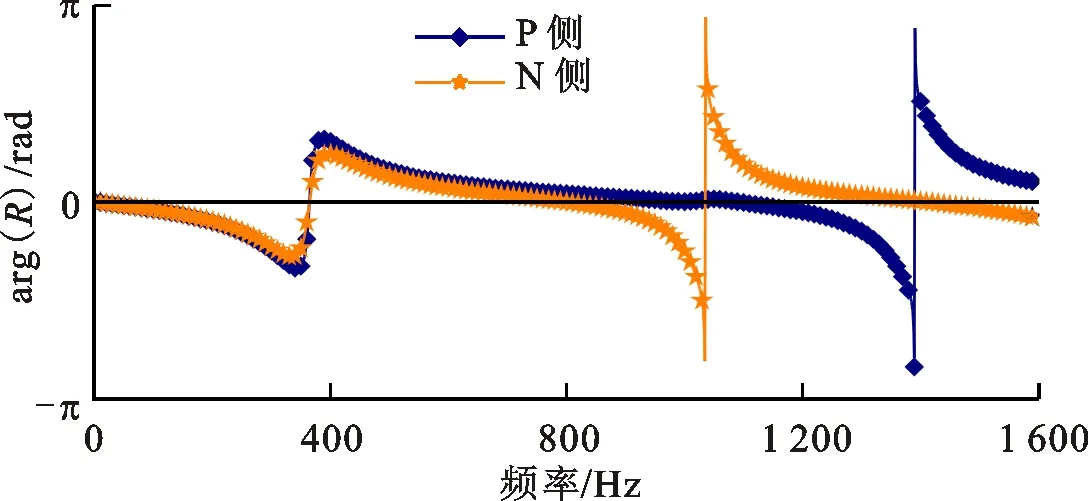
(b)反射相位图3 材料非对称型声学超材料有损耗的声学特性的仿真结果

透射幅值的峰值是结构的共振形成的,此外,共振还引起了反射相位的突变。为揭示各向异性反射相位的形成原因,图4给出了材料非对称型声学超材料无损耗的特征模态位移场。由于计算的模型是二维轴对称模型,特征模态图中虚线表示z方向的对称轴,下层薄板是尼龙材料,上层薄板是PET材料。图4a是第1阶特征模态,对应透射幅值的第1个峰值。图中上层PET薄板处于一阶共振模态,导致该侧的反射相位发生2π的突变;下层尼龙薄板的位移场类似于共振模态,该侧也发生相位突变,但是突变幅值小于2π。PET薄板处于共振模态,其共振位移大于尼龙薄板的共振位移,考虑材料损耗下PET薄板的能耗大于尼龙薄板的能耗,因此P侧的反射幅值小于N侧的反射幅值。图4b是第2阶特征模态,对应透射幅值的第2个峰值。图中下层尼龙薄板处于一阶共振模态,所以该侧的反射相位发生2π的突变;上层PET薄板处于非共振模态,位移场是以半径中点S点为对称点的反共振模态,该侧的反射相位不发生突变。尼龙薄板处于共振模态,考虑材料损耗下其变形能耗远大于PET薄板的变形能耗,因此N侧的反射幅值出现谷值。图4c是第3阶特征模态,对应透射幅值的第3个峰值。图中下层尼龙薄板处于非共振模态,该侧的反射相位不发生突变;上层PET薄板处于二阶共振模态,该侧的反射相位发生2π的突变。PET薄板处于共振模态,考虑材料损耗下其变形能耗远大于尼龙薄板的变形能耗,因此P侧的反射幅值出现谷值。共振模态还影响着透射幅值,两层薄板都处于共振模态时,结构具有较高的透射幅值,如第1个透射峰值远大于另外两个透射峰值;高阶共振模态的透射能力低于低阶共振模态的透射能力,如第3个透射峰值小于第2个透射峰值。由特征模态分析可知,反射相位在薄板的共振频率处发生突变,结构两侧不同的共振模态导致了各向异性的反射相位,考虑材料损耗下共振模态的能耗远大于非共振模态的能耗,进一步产生了各向异性的反射幅值。

(a)第1阶特征模态位移场

(b)第2阶特征模态位移场

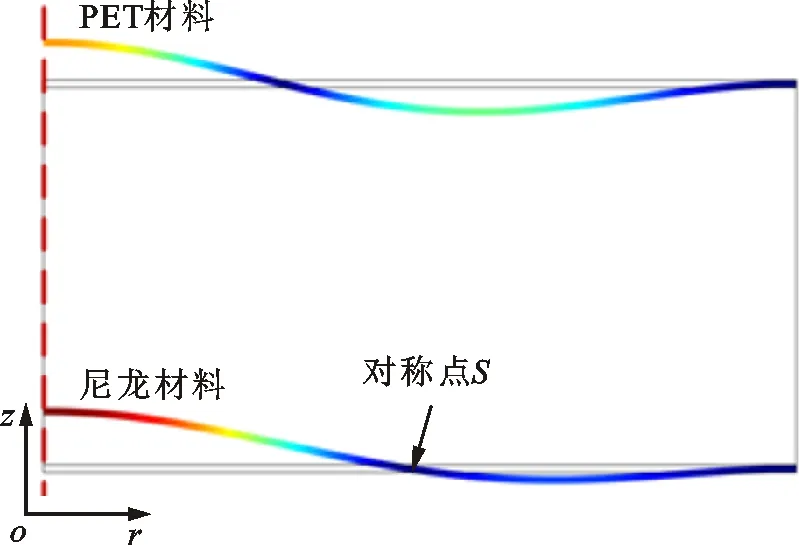
(c)第3阶特征模态位移场图4 材料非对称型声学超材料无损耗的特征模态位移场

2 几何非对称型声学超材料

材料非对称型声学超材料所用的几何模型在z轴方向是完全对称的。本节将非对称角引入薄板结构中设计几何非对称型声学超材料,其模型图和声学测试图如图5所示,该模型是折板结构,图5a是三维结构在rz平面的截图。折板的厚度t为1 mm,折板的外径r1为50 mm、内径r2为30 mm,折板与半径方向的夹角θ是结构的非对称角,θ为π/18。两层折板结构组成的几何非对称型声学超材料如图5b所示,两层折板间的距离d为10 mm,折板的外边界为固定边界。利用3D打印技术对如图5d所示的三维几何模型进行加工,加工的样件如图5c所示,选用的材料为光敏树脂,具体的材料参数见表1。由于采用方形阻抗管测量样件的声学特性,为了便于在实验中安装样件,样件的外框架是方形。图5e是阻抗管测试系统示意图,该系统包括计算机发声和处理软件、信号采集卡、功率放大器、扬声器、前管、后管和传感器等。利用前管中安装的两个传感器来测试反射系数,利用后管中安装的传感器来测试透射系数,测试样件安装在前、后管之间。

(a)元胞示意图 (b)计算双侧声学特性的示意图

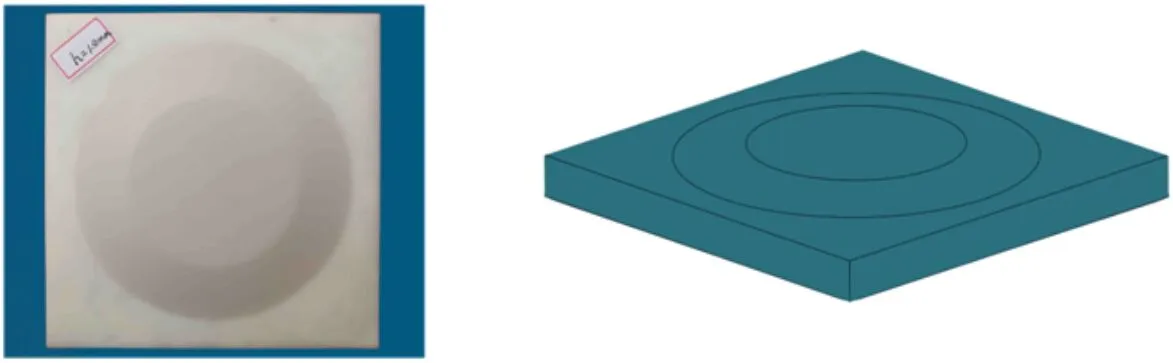
(c)实验样件(d)几何模型

(e)阻抗管测试系统示意图图5 几何非对称型声学超材料及阻抗管测试系统示意图

2.1 几何模型及实验测试系统

2.2 各向同性的反射特性及实验验证

图6是几何非对称型声学超材料有损耗的声学特性,仿真中光敏树脂材料的各向同性损耗因子为0.06。平面波从凹侧法向入射得到的声学特性记为左侧,平面波从凸侧法向入射得到的声学特性记为右侧。仿真和实验结果均表明几何非对称型声学超材料具有各向同性的反射和透射幅值。考虑材料损耗下该结构具有各向同性的反射幅值,这说明结构两侧的共振特性完全相同。由此可知,如果几何非对称不能形成共振非对称,就不能获得各向异性的反射特性。对比材料非对称型声学超材料的研究结果,进一步明确了非对称的共振特性是形成各向异性反射特性的根本原因。

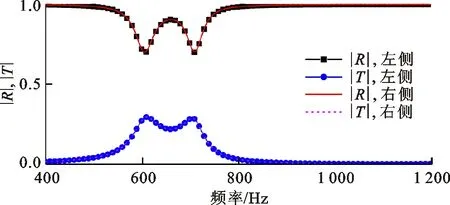
(a)反射和透射幅值的仿真结果

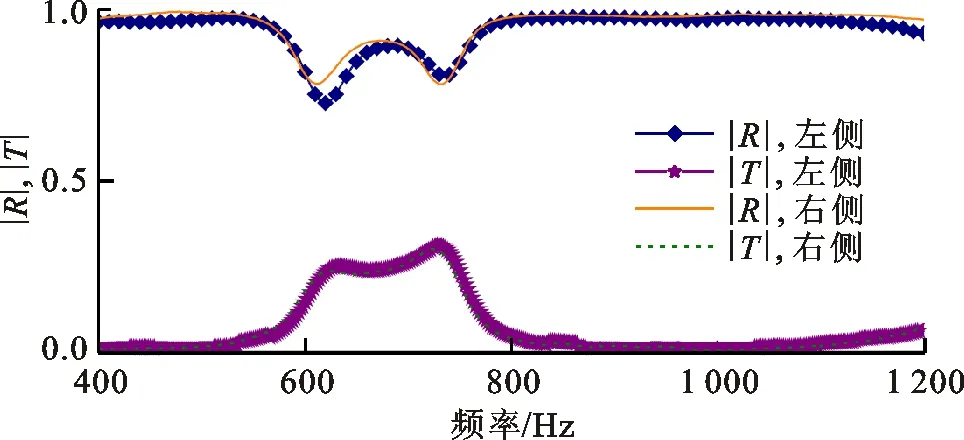
(b)反射和透射幅值的实验结果图6 几何非对称型声学超材料有损耗的声学特性

2.3 直接法求解等效参数

等效参数是描述声学超材料物理特性的一种有效手段,它从材料参数角度揭示了特殊声学特性的形成原因。本文中采用直接法求解几何非对称型声学超材料的等效参数,该方法是根据材料参数的定义推导而来[18-19]。

等效质量密度ρeff的表达式为

(1)

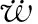
(2)

(3)

式中:p是模型受到的压力;r是模型的半径;L1和L2分别是模型反射侧和透射侧的积分边界;S是模型的外表面面积。

等效体积模量κeff的表达式为

κeff=-VTc/ΔV

(4)

其中法向压力Tc和体积变化量ΔV的具体形式分别为

(5)

(6)

式中:w是模型的位移。

等效阻抗比Zeff和等效折射率neff分别为

(7)

(8)

式中:ρ0是空气的质量密度;c0是空气中声速。

图7是利用直接法计算的几何非对称型声学超材料有损耗的等效参数。计算结果表明几何非对称型声学超材料具有完全对称的等效参数。等效质量密度在400～604 Hz范围内为负值,等效体积模量在712～1 200 Hz范围内为负值。声学超材料的等效参数特性和声学特性间具有一定的对应关系:零值等效质量密度对应透射幅值的第1个峰值,零值等效体积模量对应透射幅值的第2个峰值。零值等效质量密度是由偶极共振产生的,因此透射幅值的第1个峰值也是由偶极共振形成的;零值等效体积模量是由单极共振产生的,因此透射幅值的第2个峰值也是由单极共振形成的。被动材料要求阻抗的实部为正值,声速的虚部为正值。该要求也可以表示为等效阻抗比的实部为正值,等效折射率的虚部为负值。如图7b所示,双侧等效阻抗比的实部完全相同并且始终为正值,双侧等效折射率的虚部完全相同并且始终为负值,计算的等效参数完全满足被动材料的要求。上述分析说明直接法计算的等效参数是准确的、有意义的,因此该方法对于求解几何非对称型声学超材料的等效参数具有指导意义。

(a)等效质量密度和等效体积模量的实部

(b)等效阻抗比的实部和等效折射率的虚部图7 几何非对称型声学超材料有损耗的等效参数

3 共振非对称型声学超材料

3.1 几何模型

在2.3节研究的基础上,设计了共振非对称型声学超材料,图8是其结构示意图,右侧折板的厚度是左侧折板的2倍,其他的几何参数和几何非对称型声学超材料相同。共振非对称型声学超材料中两侧的厚度不同,所以具有非对称的共振特性。

图8 共振非对称型声学超材料结构示意图

3.2 各向异性的反射特性及实验验证

图9是共振非对称型声学超材料无损耗声学特性的仿真结果。平面波从较薄折板一侧法向入射得到的声学特性记为左侧,从较厚折板一侧法向入射得到的声学特性记为右侧。两侧的反射和透射幅值完全相同,两侧的反射相位完全不同。在透射幅值的第1个峰值处,左侧的反射相位发生2π的突变,在透射幅值的第2个峰值处,右侧的反射相位发生2π的突变。根据前面特征模态分析可知,左侧的相位突变是左侧的折板发生共振引起的,右侧的相位突变是右侧的折板发生共振引起的。虽然非对称的共振特性产生了各向异性的反射相位,但是不考虑材料损耗下两侧的反射幅值是相同的。

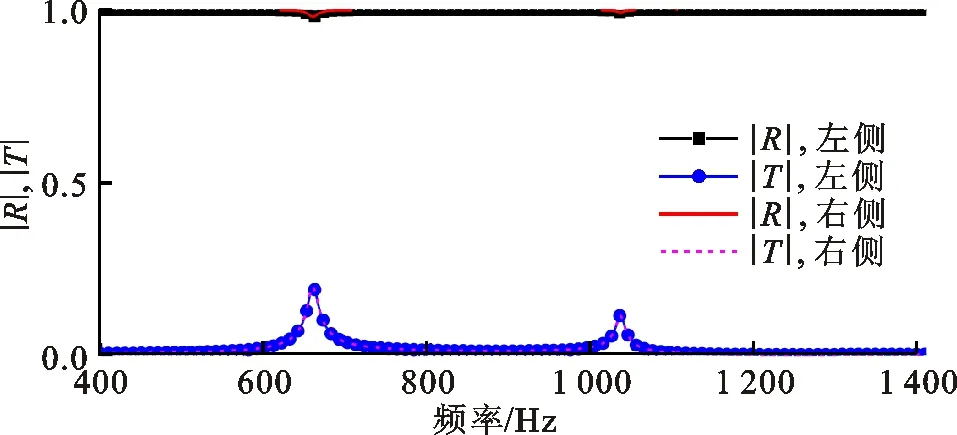
(a)反射和透射幅值

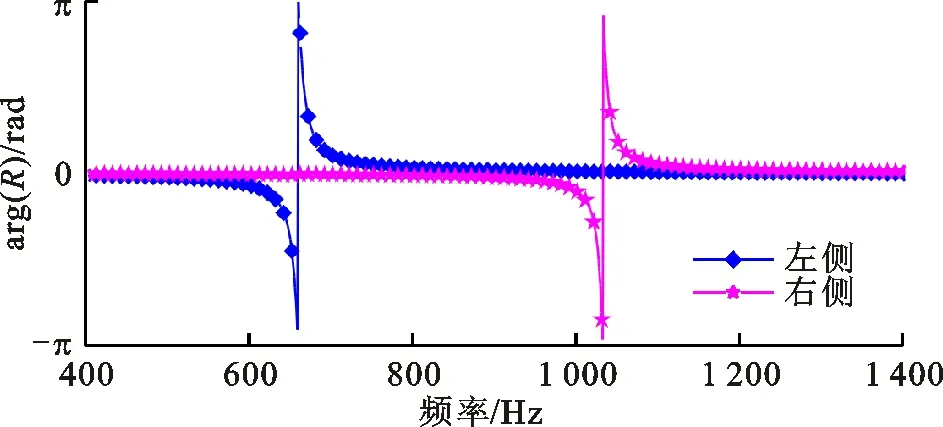
(b)反射相位图9 共振非对称型声学超材料无损耗的声学特性的仿真结果

图10是共振非对称型声学超材料有损耗声学特性的仿真结果。两侧的透射幅值完全相同,两侧的反射幅值和反射相位完全不同。在透射幅值的第1个峰值处,左侧的反射幅值出现谷值,左侧的反射相位发生突变;在透射幅值的第2个峰值处,右侧的反射幅值出现谷值,右侧的反射相位发生突变。折板的共振引起了反射相位突变,考虑材料损耗下折板共振位移变小,所以两侧反射相位突变的幅值都小于2π。考虑材料损耗下折板共振将产生能耗,左侧折板共振时,左侧折板的能耗高于右侧折板,所以左侧产生反射幅值的谷值;右侧折板共振时,右侧折板的能耗高于左侧折板,所以右侧产生反射幅值的谷值。图11是实验测得的共振非对称型声学超材料有损耗的声学特性,实验结果验证了该结构中具有各向异性的反射幅值和反射相位。仿真和实验结果均表明,仅当几何非对称形成共振非对称时,结构中才会产生各向异性的反射相位,考虑材料损耗下还能获得各向异性的反射幅值。

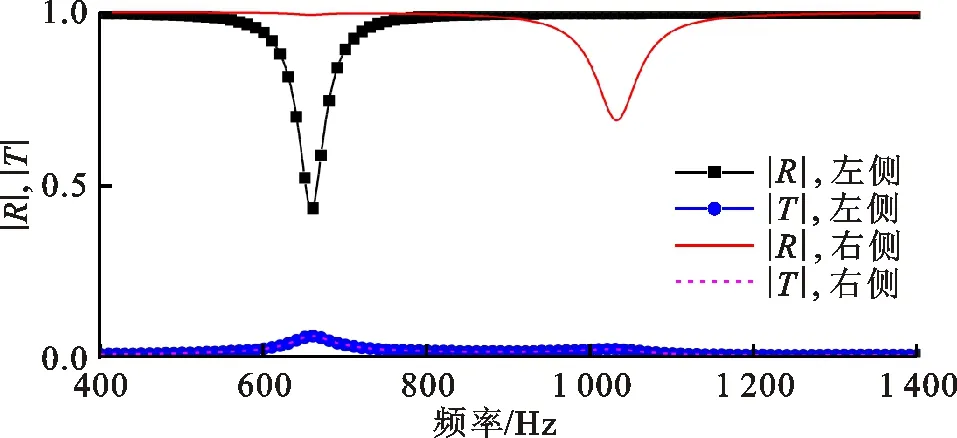
(a)反射和透射幅值

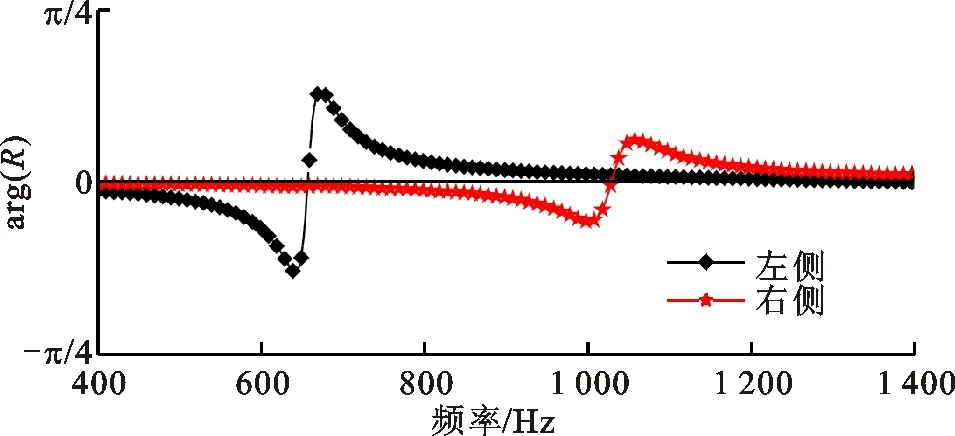
(b)反射相位图10 共振非对称型声学超材料有损耗的声学特性的仿真结果

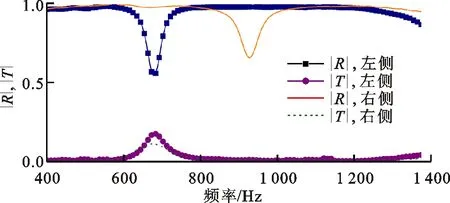
(a)反射和透射幅值

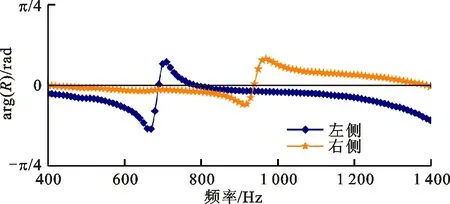
(b)反射相位图11 共振非对称型结构有损耗的声学特性的实验结果

3.3 各向异性的等效参数

图12是利用直接法求解的共振非对称型声学超材料有损耗的等效参数。共振非对称型声学超材料具有各向异性的等效参数。左侧等效质量密度在400～656 Hz范围内和1 346～1 400 Hz范围内是负值,右侧等效质量密度在400～665 Hz和705～1 029 Hz范围内是负值。左侧等效体积模量在658～1 400 Hz范围内是负值,右侧等效体积模量在1 031～1 400 Hz范围内是负值。左侧的等效参数在657 Hz都为0,该频率对应着透射幅值的第1个峰值,这是由于左侧折板在该处产生共振;右侧的等效参数在1 030 Hz都为0,该频率对应着透射幅值的第2个峰值,这是由于右侧折板在该处产生共振。上述分析表明各向异性的等效参数也是由非对称的共振特性形成的,然而各向异性的等效参数违背了被动材料的一般要求,即被动材料的材料参数是一个统一值[12]。

(a)等效质量密度的实部

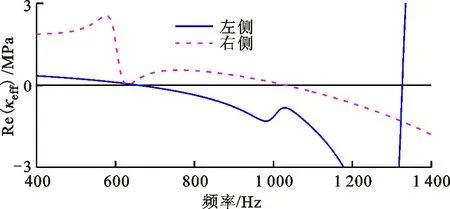
(b)等效体积模量的实部图12 共振非对称型声学超材料有损耗的等效参数

图13是共振非对称型声学超材料有损耗的等效阻抗比和等效折射率。双侧等效阻抗比的实部均为正值,满足被动材料的要求;然而左侧等效折射率的虚部在391～451 Hz范围内为正值,不满足被动材料的要求。等效参数的计算结果表明共振非对称型声学超材料的等效参数受到入射方向的影响,双侧的等效参数是各向异性的,不满足被动材料的要求。需要将平面波入射方向的影响考虑到等效参数的求解中,给出统一的等效参数,并使得求解的结果满足被动材料的要求。

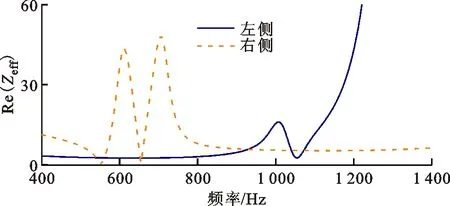
(a)等效阻抗比的实部

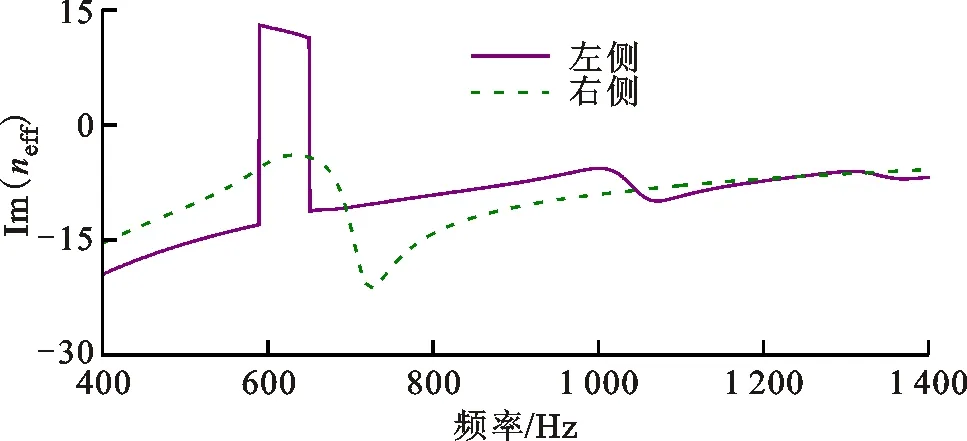
(b)等效折射率的虚部图13 共振非对称型结构有损耗的等效阻抗比和折射率

3.4 求解统一等效参数

为获得共振非对称型声学超材料的统一等效参数,需要对直接法进行改进。考虑到等效参数受平面波入射方向的影响,将模型在两个入射方向下的应力场和位移场都带入等效参数的计算。统一的等效参数可写为

(9)

(10)

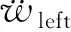
图14是利用改进的直接法计算的共振非对称型声学超材料的统一等效参数。统一等效质量密度在400～656 Hz和896～1 028 Hz范围内为负值,统一等效体积模量在658～834 Hz和1 030～1 400 Hz范围内为负值。统一等效参数在657 Hz和1 029 Hz都为0,这是由于该频率处单极共振和偶极共振产生了叠加。零值等效参数对应着透射幅值的峰值,这个对应关系确保求解的等效参数是正确的。如图14b所示,统一等效阻抗比的实部始终为正值,统一等效折射率的虚部始终为负值,两者都满足被动材料的要求。

(a)等效质量密度和等效体积模量的实部

(b)等效阻抗比的实部和等效折射率的虚部图14 共振非对称型声学超材料有损耗的统一等效参数

4 结 论

本文研究了非对称声学超材料的声学特性及等效参数,利用材料非对称、几何非对称和共振非对称3种模型揭示了非对称共振特性是形成各向异性反射特性和等效参数的根本原因。仿真和实验结果表明非对称共振特性产生了各向异性的反射相位和等效参数,考虑材料损耗下还可获得各向异性的反射幅值。本文还提出了改进的直接法用于计算非对称结构的统一等效参数。求解的统一等效参数和透射幅值间有对应关系并且满足被动材料的要求,验证了该方法的正确性。本研究工作对设计具有各向异性反射特性的声学超材料具有指导意义,并提供了一种新方法来求解非对称几何结构的等效参数。