一种适用于混合三端直流系统的差动保护方案

高淑萍,曾子璇,宋国兵,段必聪,姜元月

(1.西安科技大学电气与控制工程学院,710054,西安;2.西安交通大学电气工程学院,710049,西安)

近年来,高压直流输电(HVDC)因具有远距离大功率传输、线路造价低等优点,在电力系统中被逐步重视及应用,然而仍然存在一些急待解决的技术难题。其中,传统HVDC系统中的换相失败[1-2]是造成系统稳定性差的原因之一。

为了解决换相失败问题,混合多端直流输电系统[3]成为目前新的研究方向之一。该系统是一种新型的直流输电拓扑结构,结合了电网换相换流器(LCC)和模块化多电平换流器(MMC)两者的优势,能够实现多电源供电、多落点受电的远距离大容量输送[4],具有良好的工程应用前景。但是,由于混合多端直流输电阻抗小,故障电流幅值大、上升速度快等因素[5],低惯性直流电网直流侧一旦发生短路故障,各换流站立即向故障点馈入短路电流,使得保护难以快速地识别故障区域并动作。因此,混合多端直流输电线路的保护是混合多端直流输电发展的关键技术之一。

目前,我国的传统直流线路保护主要为行波保护、微分欠压保护、差动保护[6]等。行波保护可靠性差,易受到波头信息提取不准确、高阻接地故障等因素影响。因此,将传统直流线路保护应用在混合多端直流线路时,存在适应性问题,需要研究更高性能的保护方案。文献[7]提出了基于电流突变量的单端保护,虽然该方案可以快速可靠地区分区内外故障,但其门槛值整定的理论依据不足;文献[8]基于输电线路两端的纵向阻抗,提出了一种多端线路差动保护的改进算法,但其存在测量量较多的问题;文献[9]根据故障元件的差动电流极性特性,提出了故障全过程差动保护原理,然而该方案受直流滤波器放电及交流侧故障特征谐波影响,故障分量的波动可能会造成误动;文献[10]提出了一种基于电流突变率的高压直流输电线路纵联保护方案,利用HVDC线路中的电流突变率和特定频率下DC滤波器组来识别故障位置;文献[11]提出了基于Hausdorff距离算法的自适应线路差动保护方案,具有自适应、免整定的优良特性;文献[12]提出了基于Hausdorff距离算法的发变组大差保护新判据,该方案以线路两端额定电流相位相差90°时的Hausdorff距离作为保护判据,整定过程简单方便且不受系统参数影响;文献[13]提出了一种基于Hausdorff距离比较的快速纵联保护算法,该算法未考虑互感器不平衡电流造成的影响。

Hausdorff算法是一种快速波形相似度比较算法,在医学病理诊断方面得到了广泛应用。因该算法具有原理简单、时间窗短、计算量小、能针对性地识别波形特征、对于波形之间的差异识别灵敏度高的优点,目前国内已有专家学者将其初步应用在线路纵联保护、变压器保护等领域[11-13]。文献[14]提出了一种新型图像匹配方案,由基于SIFT特征提取方法的遗传算法与Hausdorff距离算法相结合而成,其匹配精度高、匹配速度快、抗干扰性强,但算法较复杂;文献[15]提出了一种以变压器励磁涌流和故障差流两者间Hausdorff距离为判据的变压器保护方案,此方案的抗干扰性强且计算简单;文献[16]提出了一种基于Hausdorff算法的母线保护算法,该算法将动作平面划分为3区域以自适应区分区外故障、电流互感器饱和及区内故障,具有简单、不需要整定的优点;文献[17]提出了一种适应于主动配电网的Hausdorff距离算法,适用于非精准同步的配电网络,提高了保护的可靠性。

综上所述,为保证混合三端直流输电系统的安全可靠运行,本文基于文献[14-17],对昆柳龙混合直流输电线路及T区母线进行差动保护研究,提出了利用改进Hausdorff距离算法的差动保护方案。该保护方案可以实现故障区域的判别,并实现区内外故障的判别及故障极的识别,提升了并联型混合三端直流输电线路差动保护的性能。采用PSCAD建立混合三端直流输电系统模型,利用MATLAB对故障数据进行处理,对保护方案进行仿真验证。仿真结果表明所提保护方案正确有效。

1 T型混合三端直流输电系统

1.1 系统结构

昆柳龙直流工程的并联型三端直流系统采用±800 kV混合三端直流输电系统。整流站采用由两组12脉冲换流器串联而成的LCC,逆变侧两个换流站均采用MMC结构。直流线路总长1 452 km,线路1长932 km,线路2长520 km。

图1是并联型三端混合直流输电系统结构,直流输电线路的平波电抗器为天然的物理边界,HVDC输电线路保护分为区内、区外两部分。a、b、c、d、a′、b′、c′、d′分别为各线路正极与负极出口侧的保护安装处,Z为交流侧的等值电抗。f1～f20为不同种类的故障点,将在4.1小节表1中具体介绍。

图1 并联型三端混合直流输电系统结构

1.2 T区母线结构

与传统直流线路相比,图1等值电路模型的最大特点在于T区的存在。又因逆变侧存在MMC结构,故需保护动作快速切除故障。

对于不同拓扑结构的MMC,其线路故障的特性不同,但是故障初始阶段都是以电容放电为主导,伴随少量的交流馈入[18]。因此,在对T区进行故障分析时,可将MMC换流器等效成一个RLC串联阻抗[19]。

2 直流线路故障保护原理

2.1 相模变换矩阵

对于直流正负双极间存在的电磁耦合,采用相模变换将各电气量从相域转换到模域进行研究。以线路1为例,对直流线路电气量相模解耦得到

(1)

式中:I0与I1分别为直流线路的零模电流和线模电流;Ia与Ia′分别为直流线路首端的正极电流与负极电流;S为模相变换矩阵;S-1是S的逆矩阵,为相模变换矩阵。

零模电气量在正负极线路间不能形成环流,只能流入大地,且零模分量在传播的过程中衰减较为严重。在直流线路中,只有发生单极接地故障时,线路上才含有零模分量。然而,对于不同的故障类型,线模分量却可以充分应对。因此,本文对线路的线模分量进行提取分析,构成线路区域故障判据。

2.2 故障区域判别原理

图1中,对于任意一条线路,规定电流由母线流向线路为参考方向。当非T区发生故障时,可得其故障分量等效图,如图2所示。图2中:U1f是故障点处附加线模电压源;Z1和Z2分别为线路1和线路2两侧的等效阻抗;ΔI1和ΔI2分别为经过T区两侧的故障暂态线模电流分量;Rf是故障处的过渡电阻;Ld和Zc等效为T区的等值阻抗。因ΔI1和ΔI2测量点在T区母线两侧,其参考方向为T区母线流向线路。

(a)T区母线左侧故障

(b)T区母线右侧故障图2 非T区故障等效电路

由图2a可以看出,当故障发生在T区母线左侧时,ΔI1>0,ΔI2<0;由图2b可以看出,当故障发生在T区母线右侧时,ΔI1<0,ΔI2>0。

T区母线故障等效电路如图3所示。可以看出,当故障发生在T区母线处时,ΔI1<0,ΔI2<0。

图3 T区母线故障等效电路

根据本小节分析可知,依据电流ΔI1和ΔI2的大小和方向可以实现T区故障区域的判别:当ΔI1>0,ΔI2<0时,T区母线左侧故障;当ΔI1<0,ΔI2>0时,T区母线右侧故障;当ΔI1<0,ΔI2<0时,T区母线故障。

2.3 线路区正负极电流差动保护原理

区内故障差动保护简图如图4所示。以LCC侧线路1为例,Ib为故障线路末端正极电流。取线路首末两侧电流电气量,区内故障时,Ia≠Ib,If=Ia-(-Ib)≫0。区外故障差动保护简图如图5所示。区外故障时,-Ia=Ib,Ia-(-Ib)=0。

图4 区内故障差动保护简图

图5 区外故障差动保护简图

故障区内外故障电流仿真图如图6所示。可以看出,当区内外故障时,直流线路双端电流的幅值特征不同。由此,可识别高压直流输电线路是否发生区内外故障。

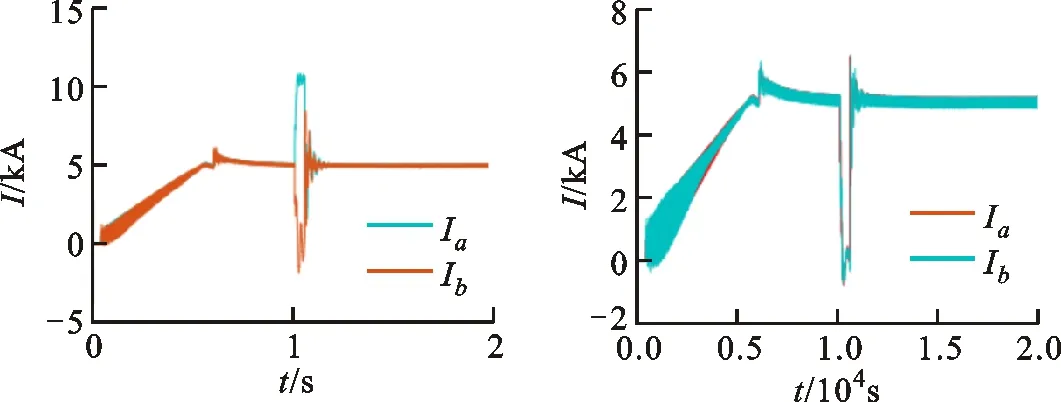
(a)单极区内故障 (b)单极区外故障

(c)双极区内故障 (d)双极区外故障图6 故障区内外故障电流仿真图

2.4 T区母线差动保护原理

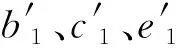
图7 T区母线保护设置点简图

2.5 Hausdorff距离算法原理

在较多种类的度量特征匹配方法中,Hausdorff距离算法以其简单有效的优点成为常用的一种算法。Hausdorff距离是一种考虑了空间目标整体形状且能描述两个点集之间相似程度的度量。Hausdorff距离没有建立在逐点对应关系上,而是通过计算2个点集之间的相似程度来衡量点集的匹配程度。因此,Hausdorff距离算法不仅简化了计算,并且可以快速有效地处理庞大数量特征点的情况。假设空间内存在两点集分别为

X={x1,x2,x3,…,xp}

(2)

Y={y1,y2,y3,…,yp}

(3)

定义点集X到Y的双向Hausdorff距离为

(4)

(5)

式中:‖·‖表示求两点集之间的距离范数;H(X,Y)为双向Hausdorff距离;h(X,Y)为从点集X到点集Y的单向Hausdorff距离;h(Y,X)为从点集Y到点集X的单向Hausdorff距离。

式(5)中h(X,Y)代表两点集间的欧氏距离。对于集合X中的元素任一xi,求取与集合Y中元素的最小距离,然后将所得最小距离集合中的最大距离视作X对Y的Hausdorff单向距离,同理可以计算Y对X的Hausdorff单向距离,两者中的较大值即为点集X对点集Y的Hausdorff距离,距离越小,则证明两组点集的相似性越大。

结合Hausdorff距离与差动保护的算法为:当区内故障时,两侧电流采样值的Hausdorff距离将远大于0,即H(Ia,-Ib)≫0;当线路发生区外故障或其他区段线路故障时,理论上Hausdorff距离将重合为0,即H(Ia,-Ib)=0。

Hausdorff距离算法与差动保护结合的优点在于其具有一定的抗非同步能力。当动作电流在非线路区内发生小幅度相移时,仍然具有辨识能力,使得直流差动保护的准确性提升。但是,由于直流电压等级高,电磁干扰大,微型计算机保护的数据采集系统易因噪声过大产生数据采集错误。为消除数据异常点对Hausdorff距离的影响,引入部分Hausdorff距离[20]:将集合X中的点到集合Y中的点的Hausdorff距离从大到小排序,考虑异常数据较少,本文舍弃集合X中Hausdorff距离最大的3个点来减少采样异常点对Hausdorff距离算法电流差动保护的影响。

根据2.4和2.5小节所述,判定T区正负极故障的Hausdorff距离算法如下。当T区母线内发生故障时,先对c1、e1两点求电流和,再用b1点电流与所求电流和作Hausdorff距离差。当T区母线故障时,H(X,-Y)≫0,非T区母线故障时,H(X,-Y)=0。由此,对于正极和负极,可分别得到

H(X,-Y)=H(Ib1,-(Ic1+Ie1))≫0

(6)

H(X′,-Y′)=H(Ib1′,-(Ic1′+Ie1′))≫0

(7)

3 基于Hausdorff距离算法的差动保护判据及流程

3.1 启动判据

以线路电流故障后的幅值变化作为启动判据,公式为

(8)

式中:ΔIp是线路的正极电流变化量;ΔIn是线路负极电流变化量。当线路故障时,电流故障分量发生较大变化,远大于0,即Kp1或Kp2大于0,因此设Kset为0.1。当线路电流满足判据式(8)时,线路故障保护启动。

3.2 故障区域识别判据

为了解决线路正负极间电磁耦合的影响,对T区两侧的采样电流进行相模变换,得到其线模电流。T区左右两侧的线模电流故障分量ΔI1和ΔI2为

(9)

式中:If1和If2为故障后电流的线模分量;In1和In2为正常运行时负荷电流的线模电流。由2.1小节分析可知,T区母线故障、T区母线左侧故障、T区母线右侧故障的识别判据分别为

ΔI1<0;ΔI2<0

(10)

ΔI1>0;ΔI2<0

(11)

ΔI1<0;ΔI2>0

(12)

3.3 线路区内外故障识别判据

根据故障线路的正极和负极电流识别区内外故障,根据2.2、2.3小节分析,以线路1为例,可得

(13)

式中:Kpp表示故障线路正极首末两端电流Hausdorff距离;Kpn表示故障线路负极首末两端电流Hausdorff距离;Ib′为故障线路末端负极电流。

依据混合直流控制特性[21],将区内外故障识别判据按额定电流IN的0.1倍整定。为可靠区分区内外故障,应针对最严重的故障情况选取保护整定值,即以区内高阻接地故障躲过区外金属性接地故障为整定原则。通过大量仿真实验可知,故障发生在区内和区外时的Hausdorff距离差异较大(Hausdorff距离算法不要求双端数据严格同步)。因此,在保留一定的裕度下,最终区内外判据选择为

Kpp<0.7&Kpn<0.7

(14)

若满足式(14)为区外故障,若不满足式(14)则为区内故障。

3.4 线路区故障选极判据

3.4.1 正负极故障判据 当发生单极故障时,由于线路的耦合作用,健全极也会受到故障极的影响。此时,需要区分故障极,从而切除故障。按躲过0.1IN整定,保留一定的裕度可得

Kpp>0.7

(15)

Kpp<0.7&Kpn>0.7

(16)

当Kpp>0.7时,判为正极区内故障;当Kpn>0.7且Kpp<0.7时,判为负极区内故障。

3.4.2 单双极故障判据 当线路发生双极故障时,线路同侧正负极电流幅值波动相同,其Hausdorff距离为0;当线路发生单极故障时,线路同侧正负极电流幅值波动相差较大,其Hausdorff距离远远大于0。以此,构成保护判据

Kpx=H(Ia,-Ia′)<0.005

(17)

式中Kpx为线路首端的正极电流与负极电流的Hausdorff距离。实际中,线路同侧正负极电流幅值存在一定的偏差,因此需对保护判据留有一定的裕度,本文通过大量仿真实验,最终设为0.005的阈值。

当Kpx小于0.005时,判定为双极接地故障,保护动作。整定值Kpx可根据实际可靠性进行调整。

3.5 T区母线故障保护动作判据

躲过0.1IN整定,保留一定的裕度,可得T区母线故障保护动作判据为

(18)

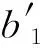
当Kpp′>0.7‖Kpn′>0.7,母线保护动作,切除T区母线故障;当Kpp′<0.7&Kpn′<0.7,母线保护不动作。

3.6 保护流程

根据3.1～3.3小节所设计的混合三端高压直流线路保护启动及故障识别判据,可得混合三端高压直流输电系统保护算法流程图,如图8所示。

图8 混合三端高压直流输电线路保护算法流程

保护算法实现的具体流程为:先进行保护启动判据,若否,则返回,继续采集数据,若是,则用线模电流故障分量大小判别故障区域,再用Hausdorff距离算法对故障区域采集到的数据进行处理,得到故障区域两端的波形相似度,进行区内外故障识别和区内故障选极,以此实现混合三端系统的差动保护。

4 仿真验证

区外故障可分为交流侧故障和换流器出口处直流线路故障,由于后者与区内故障仅隔一个平波电抗器,故障信息较为接近,识别较为困难,所以本文选取的区外故障为换流器出口处直流线路故障。此时,以区外最严重的故障情况进行仿真,即金属性接地故障(过渡电阻为0.01 Ω)。

结合实际情况,设定1 s时发生接地故障(此时系统已趋于稳定),故障持续时间为0.05 s,采样频率为10 kHz。对各线路进行PSCAD仿真,得出不同故障状态下单双极故障线路首末端电流波形。利用Matlab对故障数据进行处理,计算同线路两端线路电流幅值的Hausdorff距离。由于理论上其时间窗更短,故本文取故障后3 ms的数据进行计算。

4.1 仿真系统介绍

为测试基于幅值差动保护的Huasdorff距离算法能否满足昆柳龙直流输电工程系统,本文设置了多个不同种类的故障点f1～f20,如表1所示。

表1 故障位置及故障类型

续表

4.2 故障区域判别仿真

不同故障类型下,故障时间为1～1.03 s时,T区左侧、T区右侧、T区母线故障时的线模电流故障分量如图9～11所示。

图9 T区左侧故障时的ΔI1和ΔI2

图10 T区右侧故障时的ΔI1和ΔI2

图11 T区母线故障时的ΔI1和ΔI2

由图9～11可以看出:根据3.1小节原理能清楚区分故障发生区域;当T区左侧或T区右侧发生故障时,ΔI1与ΔI2异号,检测其故障极后,保护动作,切除故障;当T区母线故障时,ΔI1<0,ΔI2<0,由直流母线保护动作切除故障。

4.3 线路区内外故障仿真

为消除数据异常点对Hausdorff距离的影响,分别模拟直流输电线路、T区母线在区内高阻和区外金属性接地情况下的单双极故障。对PSCAD模拟所取的故障点进行数据处理,舍去Hausdorff距离最大的3个点来减少采样异常点对Hausdorff距离算法电流差动保护的影响。后续仿真在进行Hausdorff距离算法前,均首先舍去Hausdorff距离最大的3个点来减少采样值异常点。

将进行过编程处理后的数据进行Hausdorff距离运算,可得随时间变化的Hausdorff距离,如图12所示,图中实线为区内故障,虚线为区外故障。可以看出:当区内发生单双极故障时,Kpp大于保护门槛值0.7,保护动作切除故障;当区外发生单双极故障时,Kpp小于保护门槛值,保护不动作。

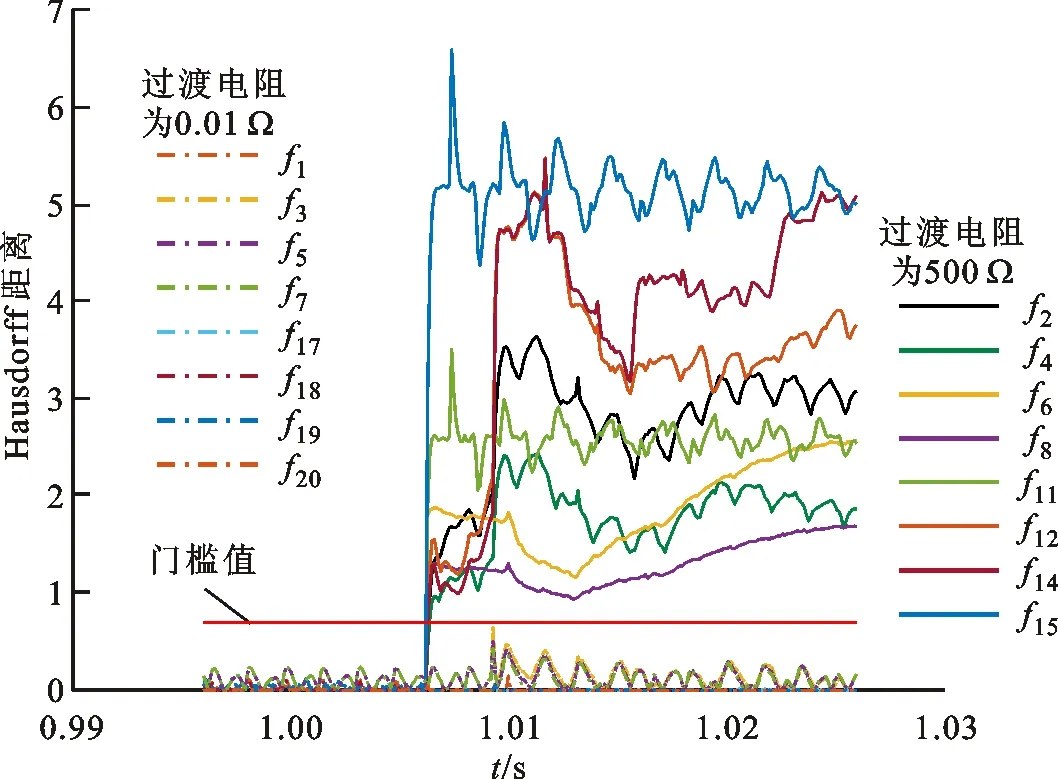
图12 区内外故障时的Hausdorff距离

4.4 线路区故障选极仿真

4.4.1 双极故障仿真结果 不同过渡电阻下,T区左侧、T区母线、T区右侧双极故障时的Hausdorff距离如图13所示。

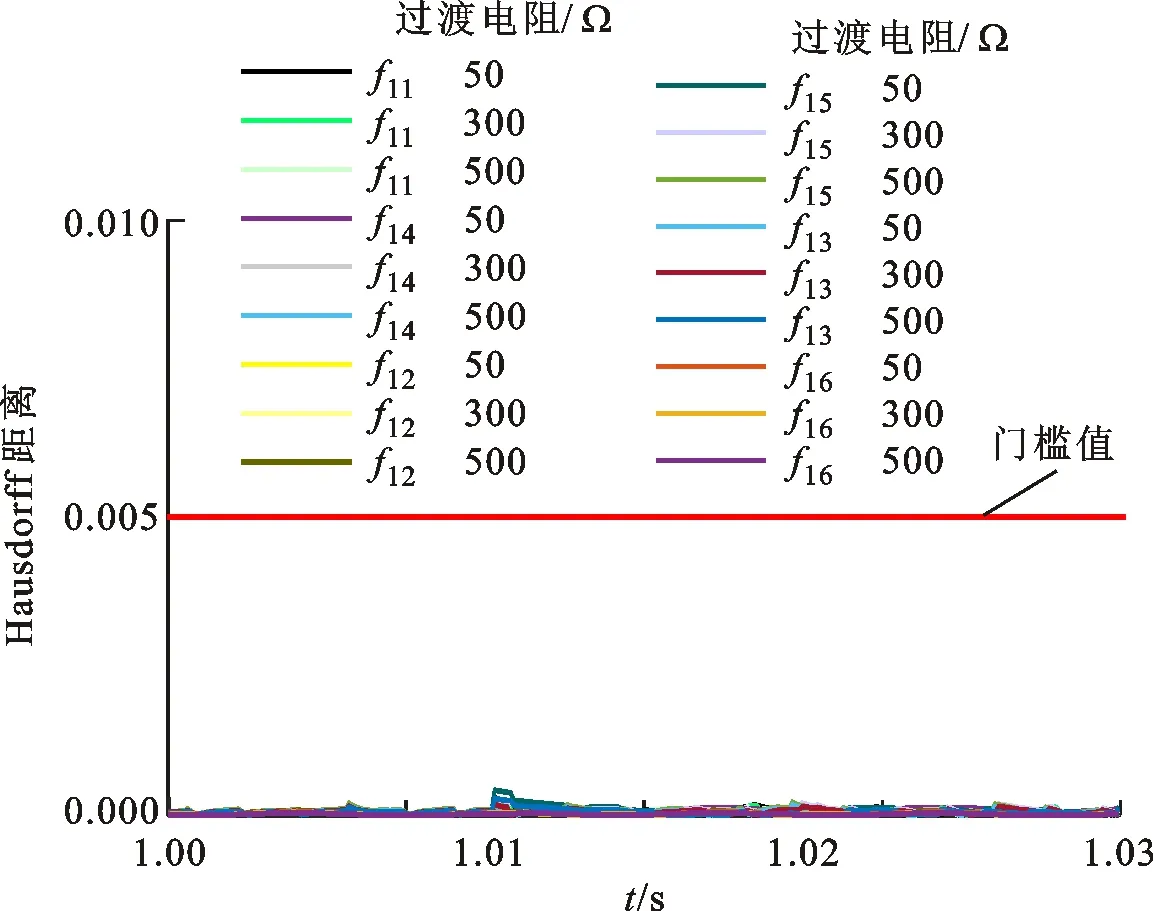
图13 区内双极故障时的Hausdorff距离

根据编程算法可得双极故障的Hausdorff距离,如表2所示。

表2 不同过渡电阻下双极故障数据

由表2和图13可以看出,Hausdorff距离算法能清楚区分单双极故障,本文Kpx的门槛值设为0.005,保护程序中设非门,当Kpx小于0.005时,双极保护装置动作。

4.4.2 正极区内外高阻故障 T区左侧、T区母线、T区右侧正极在不同过渡电阻下发生区内外故障时,Hausdorff距离如图14所示,图中实线为区内故障,虚线为区外故障。可以看出:当区内发生单极接地故障时(接地电阻为50～500 Ω),Kpp大于保护门槛值,保护动作切除故障;当区外发生单极接地故障时,应考虑最严重的故障类型——金属性接地,设其接地电阻为0.01～500 Ω,Kpp小于保护门槛值,保护不动作。

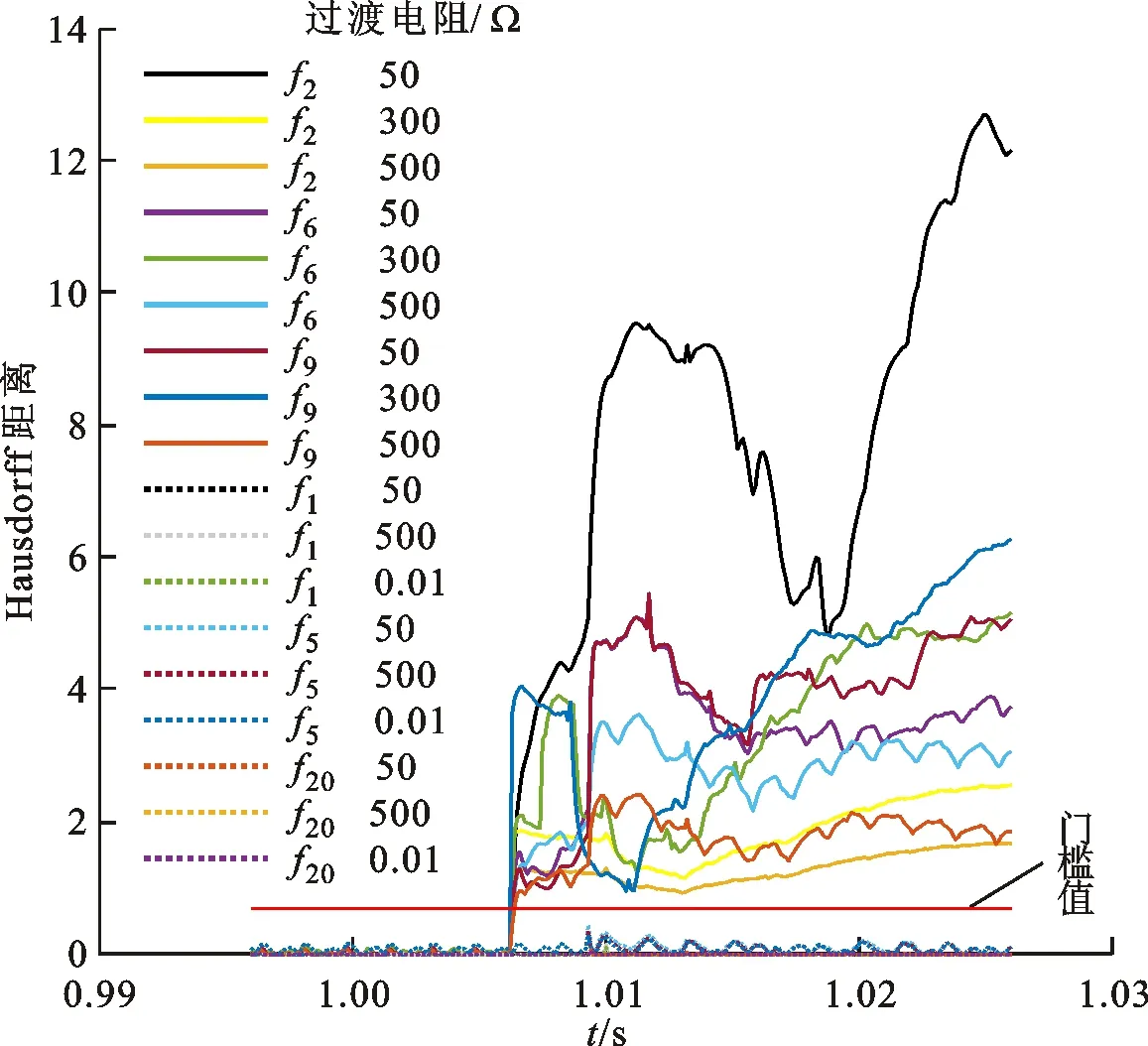
图14 区内外正极线路故障时的Hausdorff距离

因此,可通过判据式(14)(15)得出,f2、f6为区内正极故障,f1、f5为区外故障。

4.4.3 负极区内外高阻故障 当负极线路发生故障时,用保护判据式(14)(16)区分出在不同过渡电阻下的负极区内外故障,故障保护判据与正极相同,不再赘述。根据编程算法可得负极故障时的Hausdorff距离,如表3所示。

表3 不同过渡电阻下负极故障数据

由表3可知:在不同的过渡电阻下,f4、f8故障时Kpn大于0.7,f3、f7、f10故障时Kpn小于0.7。

从4.2～4.4小节可以看出,本文所提的保护方案在混合高压直流输电线路和T区母线中均可准确识别故障区域线路区内外故障,并进行故障选极。

4.5 T区母线故障保护动作仿真

对T区母线处的数据进行Hausdorff距离运算,得到随时间变化的Hausdorff距离,如图15所示,图中实线为区内故障,虚线为区外故障。可以看出:当T区内发生单双极故障(f9、f10、f13、f16、)时,Kpp大于保护门槛值0.7,保护动作切除故障;当T区无故障时,Kpp小于保护门槛值,保护不动作。

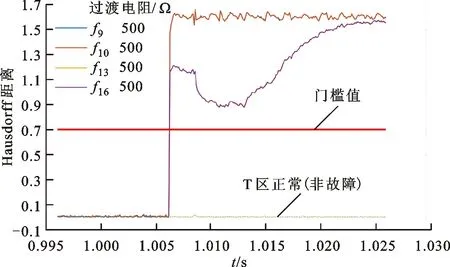
图15 随时间变化的Hausdorff距离

5 结 论

针对传统保护方案的耐过渡电阻能力差、耗时长等缺点,本文利用Hausdorff距离算法,提出一种线模电流和正负极电流相结合的针对混合三端直流输电线路的快速差动保护方案。本文结论如下。

(1)本文方案对噪声干扰、异常数据、双端通信延时有一定的降低措施,可以准确、快速辨识故障。

(2)本文方案不需要双端数据的严格同步,采样频率要求不高,仅需达到10 kHz,易于硬件实现。

(3)本文方案采样数据窗长度为3 ms,可以实现故障快速识别,减少故障对系统的危害,满足保护速动性的要求。

(4)本文方案可以识别过渡电阻为500 Ω的故障,耐过渡电阻能力强,满足保护灵敏性的要求。

(5)本文方案可以实现线路差动保护及T区汇流母线差动保护,能可靠、快速保护输电线路及T区母线,可应用在昆柳龙三端直流系统中。