平面连杆机构运动分析的三角形解法

（山东科技职业学院，山东 潍坊 261053）

前言

连杆机构的连杆往往作平面复杂运动，有时需要分析连杆平面上某点的位移、速度和加速度。用解析法作机构运动分析，以四杆机构为例，如图1所示，各杆长l1、l2、l3、l4、主动件l1角速度ω1和p点位置a、b，写出闭环向量方程L1+L2=L3+L4，其投影代数方程为：

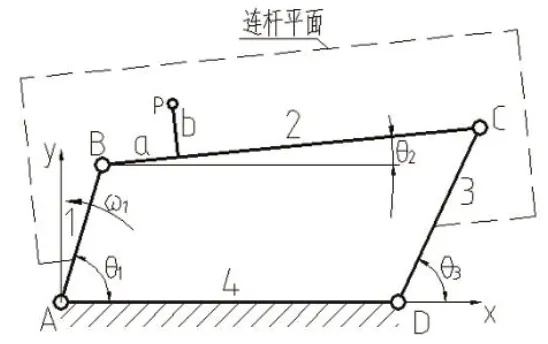
图1

（1-1）（1-2）两式组成的方程组中只有θ2、θ3两个未知数，理论上可以求出，根据几何关系，写出连杆平面上P点的坐标：

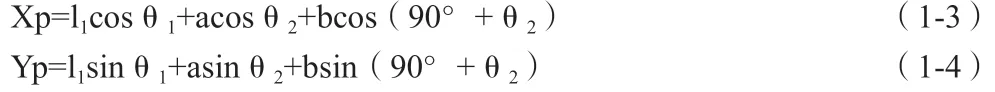
把前面求出的θ2代入，可得到P点的坐标（Xp，Yp），将（1-1）、（1-2）式对时间取一次导数，可得到：

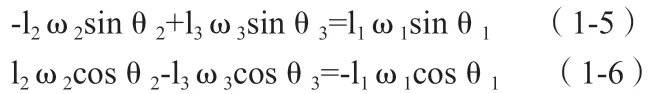
将（1-3）（1-4）式对时间取一次导数可得到P点速度，对（1-3）（1-4）（1-5）（1-6）继续对时间取导数，可求出P点的加速度，致此完成P点的运动分析。该过程的第一步求解θ2、θ3是整个运动分析的基础，但（1-1）（1-2）组成的方程组是一个超越方程组，用基本的数学变换是不能解出的，这就需要一个更好地求解θ2、θ3的方法[1]。

一、解法与思路

为了解决求解θ2、θ3的方法，以曲柄摇杆机构为例，构造出如图2所示的多个三角形。

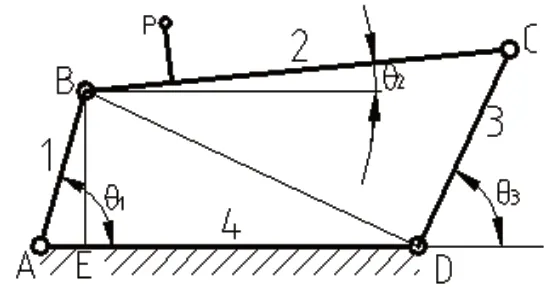
图2

在△ABE、△ABD、△BDE中，根据三角形边角关系可得到：

再利用余弦定理求出BD长度，则△BDC各边长成为已知数，在△BDC中，利用余弦定理与反正切函数结合可求出∠CBD、∠BDC，从而得到：

由式（2-1）到（2-6）即是求解θ2、θ3的过程，主动杆转到其他象限或转过特殊位置时各三角形的形状、相互位置关系会发生变化，式（2-1）到（2-6）是否仍然成立呢？下面分四种情形进行分析。

1.如图3所示，曲柄在第二象限时，ED的长度为l4加AE长度，因为θ1＞90°， cosθ1＜0，AE＜0，所以式（2-3）成立，其他关系式与第一象限完全一样。

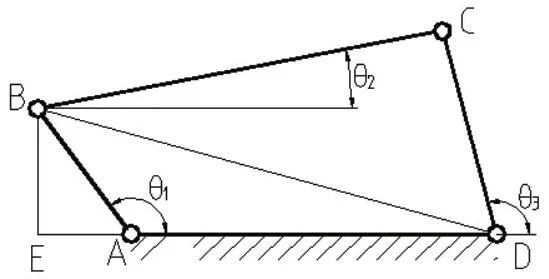
图3

2.曲柄处于第三象限且在左极限位置之前时，如图4所示。

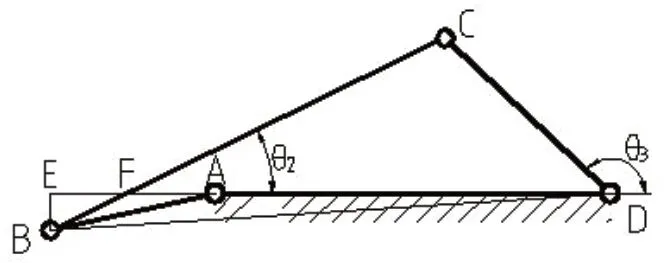
图4

此时θ2成为△BFD的一个外角，其大小等于∠CBD与∠BDE的和，因为θ1＞180°，根据式（2-1）到（2-4）计算出的∠BDE＜0，所以式（2-5）成立，按图θ3=π-（∠CDB-∠BDE）=π+∠BDE-∠CDB，考虑到∠BDE的符号，所以式（2-6）成立。

3.曲柄位于左极限位置之后或第四象限时，如图5所示。

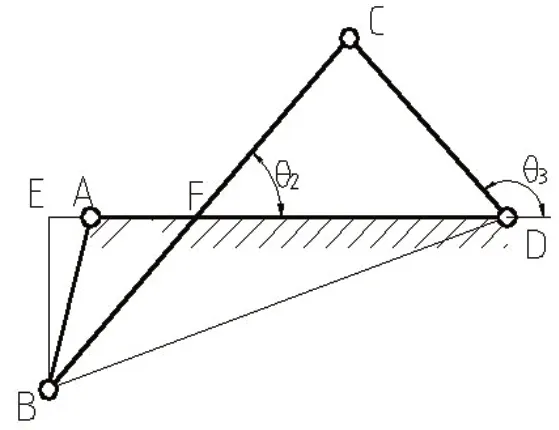
图5

分析此时的图形关系与各代数量的符号，其与情形（2）完全一致，（2-1）到（2-6）式都成立。如果曲柄与BC重合（两个极限位置），其图形位置关系与计算结果同样如此。

4.对于曲柄处于特殊位置时，与AD重合时（图形略），此时按图形得到θ2=∠CBD，θ3= π-∠BDC，按（2-4）计算则得到∠BDE=0，所以（2-5） （2-6）成立式。

由此可得到计算θ2、θ3的通项公式（2-1）到（2-6），可据此编制程序对连杆平面上的任意一点进行运动分析，θ1在0—360°以一定间隔连续取值，经过计算后可绘出P点的运动轨迹曲线、速度曲线、加速度曲线[2]。

二、结论与展望

通过构造三角形的办法，将用解析法对连杆机构进行运动分析的计算过程简化，为程序编制提供了简易可行的算法。

本文仅对曲柄摇杆机构进行了分析，根据运动图形变化关系其结论可用于双摇杆机构，对于双曲柄机构，其杆长关系，运动图形变化情形更为复杂，结论是否适用尚需进一步探讨。