基于ADRC的动态面非奇异终端滑模MDF板厚控制研究∗

陈芯锐 朱良宽 肖康铭 张 晴

（东北林业大学，黑龙江 哈尔滨 150040）

目前，中密度纤维板（Medium Density Fiberboard，MDF）已广泛用于家具制造、地板和工艺制品生产等行业。MDF连续平压热压工艺中的板厚纠偏控制研究是决定企业是否具备先进性的标志[1]。热压过程是板坯状态与参数相互作用的结果[2]。其中热压压力及温度对中密度纤维板生产过程的影响相互制约、相互依存[3]。而热压工艺中定厚段为不可逆，直接决定MDF产品的质量，因此需保证位置伺服系统的输出无超调。连续平压电液位置伺服系统借助液压缸带动液压板将板坯压缩至要求厚度，精准压制和稳定系统是压制的必要条件。在电液位置伺服系统控制中，滑模变结构控制方法因设计简单，对系统参数摄动有很强的鲁棒性，而得到广泛应用。为解决非线性系统的跟踪问题，Neha 、Wang等[4-5]分别提出一种基于扰动观测器的自适应滑模控制方法与基于分数阶观测器的自适应滑模控制方法；刘丽萍等[6]设计了一种自适应反演滑模轨迹跟踪控制器。为解决系统存在的抖振问题，提高系统的鲁棒性及优化系统的动态性能，江道根等[7]在扩张状态观测器中加入滑模控制器；陈辛波等[8]运用了一种新的自适应滑模控制算法；滕青芳、陈群等[9-10]分别提出了基于分数阶速度观测器的模型预测电流控制策略与一种RBF神经网络和非奇异快速终端滑模面的自适应控制方法；Zahedi等[11]研究了一种非线性鲁棒跟踪控制，将滑模与funnel控制相结合设计新型控制器。

但以上文献所述控制器并未消除内外干扰对系统的影响，也不能很好地观测估计扰动，同时对于系统的跟踪收敛时间没有给出相应的控制策略。为此，韩京清提出自抗扰控制技术[12]。同时，一些学者选择用非奇异终端滑模控制方法解决系统存在的扰动和不稳定问题，如王坦坦等[13]针对传统PI控制的不足,提出了一种控制效果更好的自抗扰控制策略；代明光等[14]提出了一种基于扩张状态观测器( Extended State Observer,ESO)的反演滑模控制策略；Yang等[15]研究的一种连续非奇异终端滑模控制策略，可保证在不匹配干扰条件下，任何初始状态均可在有限时间达到设定点；Qing等[16]提出了一种利用自抗扰控制实时估算设备的总干扰控制策略；Chang等[17]设计的ADRC新型控制器，提高了系统的动态性能；贾红敏等[18]将自抗扰控制策略引入到永磁同步电机位置伺服系统；Zhuo等[19]设计的自适应自抗扰控制方法，可以有效保证系统的稳定性。

基于以上研究背景，本文首先设计自抗扰控制器与三阶跟踪微分器和四阶线性扩张状态观测器。其次，利用动态面控制理论与非奇异滑模控制理论设计滑模面，进而设计动态面非奇异终端滑模控制律。然后，构造Lyapouov函数，以证明系统的稳定性。最后，通过仿真试验对该方法的可行性及有效性进行验证。

1 系统描述

1.1 电液位置伺服系统

MDF连续平压电液位置伺服系统组成部分主要有电液伺服阀、伺服放大器及四通阀控液压缸，如图1 所示。液压缸活塞在定厚段的位移经由位移传感器转化成位置信号，与给定位置信号比较形成偏差信号输入控制器，由控制器通过内部算法将偏差信号转换成输入电压信号，再由伺服放大器将电压信号转换成电流信号用以控制伺服阀阀芯运动，进而使一定量的油液进入内部推动活塞运动，即活塞带动负载将板坯压至既定厚度。系统中伺服阀采用零开口四通滑阀，其结构如图2 所示。

1.2 系统模型

本文将具有单个四通阀控制液压缸的液压系统作为被控对象，其动力机构的3 个基本方程如下[20-23]：

式中：QL为负载流量，m3/s；Cd为滑阀流量系数，w为滑阀节流窗口面积梯度，m；xv为阀芯位移，m；ρ为液体密度，kg/m3；PS为供油压力，MPa；PL为负载压力，MPa； AP为活塞有效面积，m2；y为活塞位移，m；Ctc为总泄露系数，Vt为t时刻液压缸油腔容积，m3；t为系统工作时间， s；βe为油液弹性模量，MPa；m为负载总质量，kg；Bc为粘性阻尼系数，N·s/m；KL为负载弹性刚度，N/m；F为外负载力，N 。

将伺服阀与伺服放大器近似成比例环节，可表示成：

在实际的连续平压电液位置伺服系统中，参数和复合干扰均是不确定且有界的。

2 基于ADRC的动态面非奇异终端滑模控制律设计

基于ADRC的动态面非奇异终端滑模控制律是由跟踪微分器( Tracking Differentiators,TD)、线性扩张状态观测器( Linear Extended State Observer,LESO)及动态面非奇异终端滑模（DSNTSMC）控制器组成，其控制器结构如图3 所示。

图3 控制器设计结构图Fig.3 Structure diagram of controller design

2.1 跟踪微分器设计

根据控制器设计要求，给定输入信号r的过渡过程x1，同时产生其微分信号x2和二阶微分信号x3,三阶跟踪微分器的离散化表达式为：

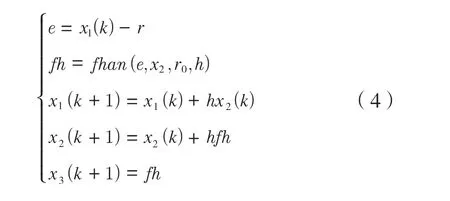
式中：e为输入误差，h为积分步长，r0为速度因子，fhan为最速控制综合函数[12]。

2.2 线性扩张状态观测器

线性扩张状态观测器是自抗扰控制的核心组成部分，可以对系统的内外不确定性干扰进行实时估计观测。针对式（3）所示，令Δf(x)+Δg(xv)u+d=x4，即x4为系统内外不确定干扰总和。则系统式（3）可以扩张成以下状态空间表达式：

根据文献[12]，可以得到式（5）的线性扩张状态观测器表达式为：

式中：z=[z1，z2，z3，z4]T分别为变量x=[x1，x2，x3，x4]T的估计值。观测器输出信号z4为系统内外不确定干扰的估计值。τ=[τ1，τ2，τ3，τ4]T为线性扩张状态观测器的增益系数。利用带宽定义可以确定增益系数的取值，简化参数的选取工作。令增益系数为：

式中：ω0表示观测器的带宽，ω0一般越大，LESO的估计效果越好，但要根据实际情况确定，ω0＞0。 α1，α2，α3，α4需是多项式满足Hurwitz条件[24-25]，即：(s+1)4=s4+α1s3+α2s2+α3s+α4，（其中s仅为变量符号，并无实际含义）。

则α1=4，α2=6，α3=4，α4=1。因此选取合适的ω0值，可保证观测器对于干扰的准确估计观测。

2.3 动态面非奇异终端滑模控制器设计

2.3.1 控制器设计

本文所设计的控制器，结合了动态面控制、非奇异终端滑模控制及自抗扰控制的思想，控制器设计的目的是最终使各个状态变量误差在有限的时间内收敛为零，保证系统的稳定性。

系统的误差方程为：

根据式（22）可知：系统状态半全局一致有界，跟踪误差e1→0，e2→0，因此可知式（14）可以满足：

因此要保证式（22）成立，需要保证e3→0，即进行下一步设计。

第3 步：为使e3→0，引入非奇异终端滑模面：

式中：α，β为滑模面参数，α＞0；1＜β＜2。

结合扩张状态观测器，将控制器设计为：

式中：ρ1＞0，ρ2＞0，ρ3＞0，为控制器待选取参数，ρ1，ρ2为观测器对不确定观测误差的上界，因此令ρ1+ρ2=σLESO，z4为系统对内外不确定干扰总和的估计值。

2.3.2 稳定性分析

针对Lyapunov稳定性原理可知，需要证明系统状态误差在有限的时间内收敛到零，即整个控制系统满足Lyapunov原理下的稳定性条件。

结合式（24）可知：

定义Lyapunov函数为：

对式（27）求导，并将式（25）和式（26）带入到求导中，得到：

综上所述，系统的所有状态为半全局一致有界，跟踪误差渐近为零。

3 仿真分析

根据实际工艺，系统的主要标称参数如下所示[21]：

Ksv=0.01 m/A，Ka=0.012 5 A/V，

Cd=0.61，ρ=850 kg/m3，A=0.125 6 m2，

Bc=2.25×106N·s/m，K=2.4 GN/m，

Ps=25 MPa，Ct=5×10-6m5/Ns，

ω=0.025 m，βe=685 MPa，F=54 780N，

Vt=2.365×10-3m3，m=1×103kg，

PL=16.67 MPa

令液压缸上活塞的初始位置为x0=0，对板坯进行0.1mm的微调，给定的期望位置信号为yd=0.1mm，对其进行位置跟踪。为验证本文设计控制器的收敛速度和稳定性，现将其与传统滑模控制器和经典PID控制器进行对比。

同时，为验证本文提出的控制器具有良好的抑制扰动的特性，对系统突加一种负载扰动，对系统的位置跟踪和响应速度进行观测。

选取TD参数：r0=100，h=0.01;LESO参数：ω0=15;控制器参数：

1）动态面控制参数：c1=0.05，c2=0.05，τ=1。

2）滑模面参数：α=16，β=5.5。

3）控制器参数：σLESO=0.000 1，ρ3=0.002 5。

根据试凑法及经验选取PID控制器比例积分微分系数，分别为：kp=20 000，ki=40，kd=50。

经调试选取传统滑模控制参数：c1=400，c2=1×103，ŋ=80。

仿真结果如图4～8 所示。如图4 所示，本研究设计的控制器收敛速度明显优于经典PID控制器和传统滑模控制，控制精度相对更高。且经局部放大曲线，可知DSNTSMC对系统的控制无超调现象。

图4 3 种控制器的位置跟踪对比Fig.4 Position tracking comparison of 3 controllers

图5 给出了3 种控制器的输出信号变化曲线，可以看出，本文设计的控制器的控制数量没有出现大幅抖振，虽然峰值相对较高，但是相对于其他两种控制器而言，收敛时间更短，效果更强。

图6 与图7 表明，本文设计的DSNTSMC相比传统滑模具有更快的收敛速度，可以使系统在很短时间内到达滑模面上，且到达滑模面后，DSNTSMC可使第三个子系统的跟踪误差在有限时间内收敛到零，而传统滑模控制只能实现渐近收敛。

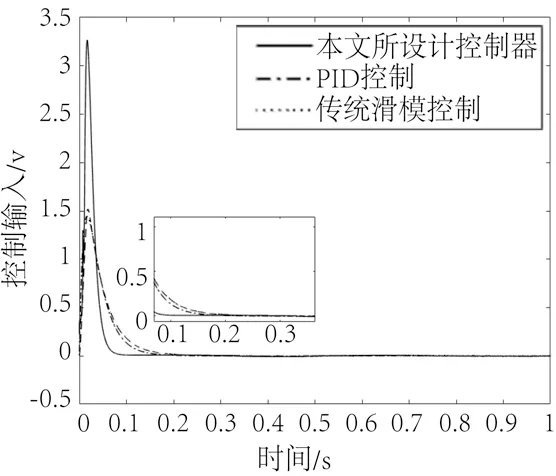
图5 3 种控制器的输出电压Fig.5 Output voltage of 3 controllers

图6 滑模面趋近过程Fig.6 The approach process of sliding die surface

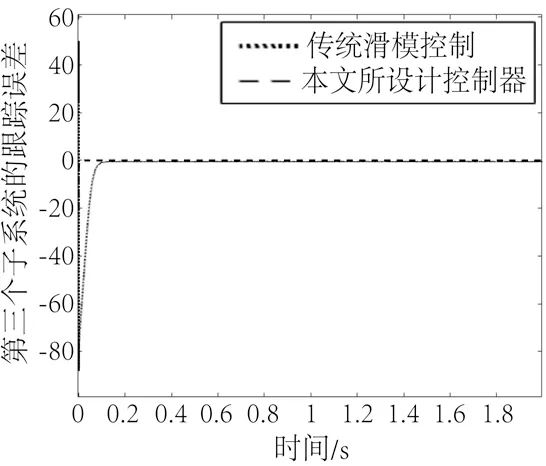
图7 第三子系统的跟踪误差Fig.7 Tracking error of the third subsystem

图8 表明，尽管系统的内外不确定干扰变化加快，但是线性扩张状态观测器仍然可以对干扰进行实时准确的估计观测。

图8 LESO观测曲线Fig.8 LESO observation curve

4 结论

针对中密度纤维板板厚纠偏位置伺服系统存在内外干扰及在干扰条件下影响快速准确位置跟踪的问题，设计了一种基于ADRC技术的动态面非奇异终端滑模控制策略。利用线性扩张状态观测器对系统的内外不确定干扰进行实时估计观测，利用所设计的控制器加快系统的收敛速度，减小稳态误差及超调。仿真结果验证了该算法收敛速度快，能够达到良好的控制效果。所述方法可以缩短系统动态响应时间，在估计观测干扰过程中，可以进行准确观测。无超调和抖振现象，增强了系统的可靠性及稳定性，提高了系统控制精度。