考虑集群划分的配电网网源协调扩展规划

丁 明，张 宇，毕 锐，胡 迪，高平平

（合肥工业大学安徽省新能源利用与节能重点实验室，合肥 230009）

配电扩展规划是指在满足负荷增长和网络现状的情况下，对线路、变电站等进行优化，以满足用户的用电需求[1]。随着大量分布式电源DG（distrib⁃uted generation）接入电网，部分地区已经出现渗透率大于100%的情况，给系统的安全经济运行带来影响，导致电压越限、功率倒送、网损增加等[2-4]。因此，亟需研究配电网与分布式电源的协调规划问题。

目前，国内外在含DG的配电网扩展规划领域取得了一定的理论和应用成果：文献[5]以减少配电网规划总成本为目标，建立了计及含DG的区域综合能源系统的配电网扩展双层规划模型；文献[6-7]考虑分布式电源对配电网网络拓扑结构影响，采用双层规划方法对线路结构及DG位置容量进行优化；文献[8]计及网架动态重构的影响，优化对DG的消纳能力与网络拓扑结构。针对高渗透率DG的消纳问题，以及对配电网扩展规划的影响，文献[9-10]考虑源荷匹配问题，通过协同规划降低DG弃用水平；文献[11]基于完全信息动态博弈理论，以光伏、储能和电网作为博弈参与者建立协调规划模型，以提高电网消纳光伏的积极性。上述对含DG的配电网扩展规划研究多采用对分布式电源的集中控制或单独直接控制，随着分布式发电呈现出高渗透率、小型化、分散化的特点，传统的分布式电源集中控制模式将难以满足运行控制阶段的要求。而基于集群的分布式能源发电模式由于其稳定、高效、灵活、友好的并网特性，为分布式能源的大规模消纳提供了新模式[12]。因此，以集群为单元进行配电网和DG运行控制与规划已经成为一种发展趋势。

在分布式发电集群划分及应用方面，文献[13]提出改进的模块度指标，综合考虑区域无功平衡与节点间无功电压灵敏度进行集群电压优化控制；文献[14]提出面向分布式光伏有源配电网的虚拟集群概念，并基于社团理论提出适应调控目标变化的虚拟集群动态划分方法；文献[15]采用调节关键节点处光伏逆变器无功功率的策略，将电力系统划分为多个集群进行无功优化。文献[16-17]分别基于集群划分结果进行了分布式电源的选址定容规划与储能容量规划，但没有涉及网源规划间的协调性问题，且是在网架结构、DG接入和集群划分结果均固定的基础上进行的，没有考虑网络的动态变化与集群划分间的动态适应与交互影响问题。

针对目前考虑集群划分的规划方法尚未考虑网源规划的协调性，以及集群划分结果不能适应DG和网络的动态变化的问题，本文建立了考虑集群划分的配电网网源协调扩展规划模型，重点解决规划中配网与DG规划的协调性及网源动态变化与集群划分的动态匹配问题。该模型采用分层交替迭代优化方法：上层规划模型以年综合费用最小为目标，在给定集群划分结果下，对网络拓扑结构与接入各集群的DG位置、容量进行规划；在下层划分模型中以新的网络拓扑结构与DG配置为基础，以兼顾模块度与有功平衡度的综合性能指标最佳为判据，重新进行集群划分，所得划分新方案反馈给上层规划。整个优化过程迭代进行，采用改进混合遗传算法求解。文中给出了相关模型、算法、算例结果及讨论。

1 考虑集群划分的配电网网源协调规划双层优化模型

1.1 双层优化架构

当线路选择发生变化时，节点间的电气耦合关系发生改变进而影响模块度指标；DG接入位置容量改变则会直接影响到有功平衡度指标。传统的集群划分方法建立在网络拓扑结构与DG出力已知的前提下，无法对待规划配电网络进行划分。并且集群划分与网源协调规划，单独而言，都属于复杂的优化问题；两者具有不同的量纲，难以建立统一的优化模型直接求解；当两者联合优化时，集群划分建立在网源已知的基础上，属于分层优化的范畴[18]。因此本文将规划模型分解为两层进行迭代求解，该双层优化架构如图1所示。

图1 双层优化模型架构Fig.1 Framework of bi-level optimization model

上层规划模型目标函数为综合支出年费用最小；决策变量为线路选择和DG安装位置容量；约束条件包括潮流约束、节点电压与线路电流上下限约束、DG渗透率约束、网络辐射状与连通性约束。下层集群划分模型目标函数为集群综合性能指标最大，决策变量为系统各节点线路所属集群。

上下层之间的参数传递关系：两层优化模型的目标函数、约束条件与决策变量各不相同，但上下层优化过程互相耦合，需要通过参数传递进行迭代寻优：上层规划模型将决策变量（即网络拓扑与DG配置情况）传递给下层，作为下层优化的初始条件；下层划分模型在此基础上对配电网进行集群划分，将决策变量作为参数返回到上层规划的目标函数与渗透率约束中。

1.2 上层费用优化模型

上层规划模型以年综合费用最小为目标，建立包含DG与配电线路投资与运行年费用、集群网损费用和系统购电费用的目标函数。

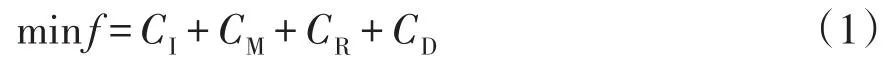
式中：f为综合支出年费用；CI为DG与配电线路投资费用；CM为DG与配电线路运维费用；CR为集群网损费用；CD为系统购电费用。各项费用的计算公式如下：

（1）投资费用

式中：r为折现率，本文取10%；n为投资回报期限；B为网络中不同线路的分类集合，B={EFF,NAF}，集合中分别表示现有不可更换线路和新增线路；AL为线路单位长度投资成本；li为线路i的长度；xL,i、xDG,i为0-1变量，分别表示线路与DG的投资变量，若为1则投建，否则不投建；CI,DG为DG的单位容量投资成本；为节点i处DG的规划容量；ΩN、ΩDG、ΩDGs分别表示网络节点集合、DG待建节点集合、DG待建与已有节点集合。

（2）运维费用

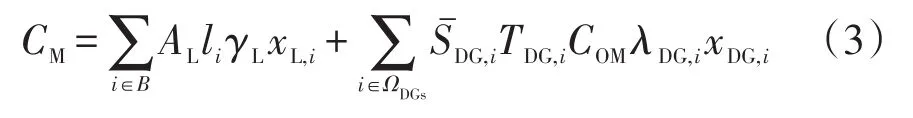
式中：γL为线路运维费用率；TDG,i为节点i处DG年发电运行小时数；COM为DG单位容量运维费用率；λDG,i为第i个节点的分布式电源功率因数。

（3）网损费用

式中：T为年最大负荷损耗小时数；H为集群个数；Nclu,l为集群clu包含的线路数量；ZL为单位长度线路阻抗幅值；Ii为线路i的电流平方值；Ce为系统单位电价。

（4）系统购电费用

式中，Pclu为网络流入集群clu的净功率。

综合考虑配电网规划和运行的实际情况，上层优化模型的约束条件包括电气约束和网络约束。其中电气约束包括配电网潮流约束、节点电压与线路电流约束、DG接入比例约束；网络约束包括辐射状约束与连通性约束。具体描述如下：

（1）配电网潮流约束

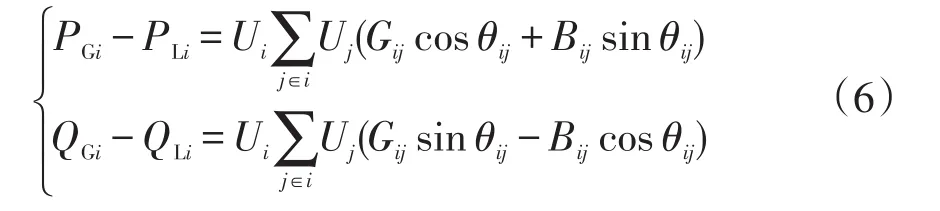
式中：PGi和QGi分别为节点i处电源的有功和无功出力；PLi和QLi分别为节点i处有功和无功负荷；Ui和Uj分别为节点i和j电压幅值；Gij和Bij分别为支路i、j的电导、电纳；θij为节点i,j间相角差；j∈i表示与节点i相邻的节点。

（2）节点电压与线路电流约束

式中：Ui为节点i的电压幅值；Ui,min、Ui,max分别为节点电压的上下限；Ii为线路i的电流幅值；Ii,max为允许通过线路的电流上限。

（3）DG渗透率约束

DG接入比例过高将引起电压越界、电流过载等问题，本文以DG系统渗透率λsys约束系统总DG装机容量，其定义为

式中：ΩL表示负荷节点集合；为节点i处最大负荷值。

DG系统渗透率约束为

同时，为了减少集群向配网倒送功率，以DG集群渗透率λclu约束集群内DG装机容量，其定义为

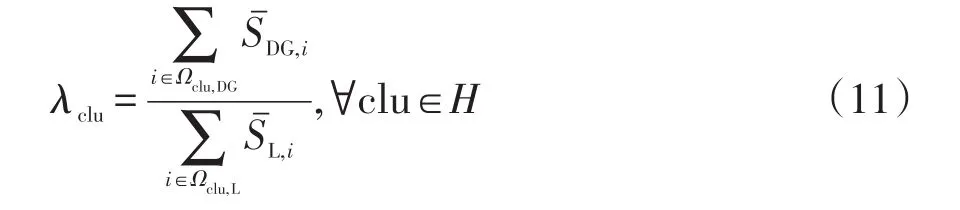
式中：Ωclu,DG表示集群clu内DG安装节点集合；Ωclu,L表示集群clu内负荷节点集合。本文取λclu=1.0。

（4）辐射状与连通性约束

配电网运行要求每个负荷均能被供电，禁止出现孤岛、孤链与环网，网络拓扑满足辐射状与连通性。本文采用基于Prim最小生成树算法[19]的编码方式生成初始网络并对不可行解进行修复，使网络拓扑结构自动满足辐射状与连通性约束。

1.3 下层集群划分模型

下层优化模型以集群划分综合指标最优为目标，考虑网络拓扑结构、电气距离、DG配置等因素，使得集群划分结果满足集群内节点电气联系紧密群间联系松散，提高集群内DG就地消纳能力。集群划分综合指标为

式中：φC为集群模块度指标；φP为集群有功平衡度指标。

（1）集群模块度指标φC

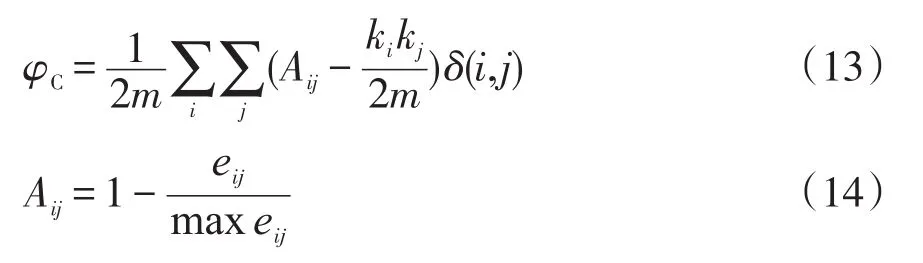
式中：Aij为节点i与节点j的电气距离函数，表示两节点间电气距离权重；m为所有边权之和；ki为与节点i相连线路权重之和；若节点i与节点j在同一集群，则δ(i,j)为1，否则为0。

模块度常用于复杂网络的社区检测，以衡量网络的社区结构强度，当网络边权表达发生变化时模块度指标表示不同的意义。本文以电气距离定义边权，用来表征两个节点之间联系的密切程度，由电压与功率间的灵敏度关系求得。对于包含n个节点的系统，基于无功电压灵敏度矩阵的电气距离可表示为

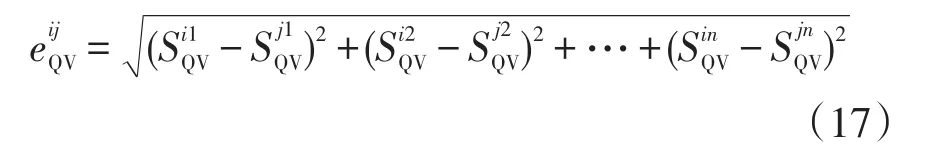
（2）集群有功平衡度指标φP

在分布式电源安装容量不均衡的情况下，为了实现分布式电源的协同规划，以电网侧集群特性指标——有功平衡度来对集群进行划分，指导DG的具体安装位置及容量。集群有功平衡度高表示现有DG安装容量及输出功率与负荷匹配程度高，有功平衡度低的集群匹配程度低，可继续增加DG。以集群净功率表征的有功平衡度为

式中：φclu,i为集群i的有功平衡度；Pclu,i为集群i的净功率特性；φP为系统的集群有功平衡度指标。

2 基于改进混合遗传算法的模型求解策略

针对考虑集群划分的配电网网源协调规划双层优化模型的求解是一个复杂的混合整数规划问题。下层划分模型实现配电网络节点划分，将各节点划分结果传递给上层模型；上层规划模型根据集群划分结果进行DG选址定容并确定网络拓扑结构，并将DG位置容量与网络拓扑结构传递给下层模型，重新进行集群划分。本文采用基于改进遗传算法的混合智能优化算法求解该模型。

2.1 求解方法

上层规划模型中，传统遗传算法编码方式无法同时满足网络拓扑规划的连通性、辐射性要求及DG接入比例限制，本文采用混合编码方式，如图2所示，将染色体分为“待选线路”与“DG容量”两部分。“待选线路”部分染色体Xi采用二进制编码，0表示未选中，1表示选中。为了避免遗传算法随机性带来的大量不可行解，在产生初始种群时，对n条待选新建线路随机赋整数值1～n作为边权，基于边权值采用Prim最小生成树算法得到树形结构，译码为邻接矩阵表示，作为下层染色体。下层优化结束后，将邻接矩阵翻译成0-1二进制表示。生成的初始网络自然呈连通、辐射状，避免了由随机赋值导致的“整体偏差”。“DG容量”部分染色体Ci采用基于隐形编码方式的实数编码。以dDG作为DG单位安装容量，本文取dDG=100 kV·A，每个DG待选安装节点的安装容量为nidDG。其中基因位i表示第i个待安装节点，基因n表示安装容量为单位安装容量的倍数，n=0表示不安装DG。

图2 上层染色体串Fig.2 Chromosome string in the upper-layer

为了增强算法全局寻优能力，引入自适应算子[20]概念调整交叉、变异概率。改进后的算子将低于平均适应度值的个体交叉、变异概率提高，使其淘汰；将高于平均适应度值的个体交叉、变异概率降低，使其遗传至下一代。调整公式为

式中：fmax为最高适应度值；f为一对交叉个体中较大的适应度值；favg为种群平均适应度值；f′为变异个体适应度值。其中k1＜k2，k3＜k4，本文取k1=k3=0.1，k2=k4=0.85。

在遗传操作过程中，当算法迭代次数等于某限定值时，终止搜索，即

式中：gennew为算法当前迭代次数；genset为设定算法最大迭代次数；本文取收敛判据genset=200。

下层模型选择集群划分综合指标作为适应度值，基于网络邻接矩阵对染色体进行编码。上下层编码传递方式如图3所示，下层算法的详细流程见文献[12]。

图3 染色体编码方法Fig.3 Chromosome encoding method

2.2 混合遗传算法求解流程

采用改进混合遗传算法求解本文提出的分层迭代优化模型的主要流程如下。

步骤1初始化。读取配电网运行模拟相关数据，设置遗传算法参数；

步骤2初始化上层种群。采用Prim最小生成树法产生初始网络拓扑结构，采用隐形编码方式得到DG安装位置容量初始解；

步骤3更新上层种群。进行潮流计算，将上层网络拓扑结构与DG位置容量作为基础参数传递到下层模型优化；

步骤4进行下层优化，步骤如下：

（1）初始化下层种群。将上层染色体“待选线路”部分基因译码为邻接矩阵进行下层染色体编码，产生下层初始种群；

（2）更新下层种群并计算适应值。读取上层潮流计算结果，计算综合性能指标ρ值；

（3）下层终止条件判断。判断下层是否满足收敛条件，若是则转向步骤5，否则执行4；

（4）下层遗传算子操作。对下层种群中个体进行选择、交叉、变异遗传算子操作，并转向2；

步骤5计算上层适应度值。读取下层集群划分结果，计算上层目标函数值f，对个体按适应度大小排序，更新种群累计适应度值、历代平均适应度值、历代最佳适应度值与个体最优值；

步骤6上层终止条件判断。判断上层是否满足收敛条件gennew=200，若是则输出最优方案，否则执行步骤7；

步骤7上层遗传算子操作。采用轮盘赌选择并加入精英保留策略，引入自适应算子调整交叉、变异概率，返回步骤3。

3 算例分析

3.1 算例系统概述

采用某10 kV配电网络进行算例分析，初始网络拓扑结构如图4所示，图中实线为已有线路，虚线为待选线路。该网络具有10个节点、2条已有支路和14条待选扩建线路，其中节点1与高压系统相连，其余节点均为负荷节点且可接入DG。节点3、6、9、10已安装DG容量分别为0.3MW、0.6MW、0.9MW、0.6 MW，支路参数参见附录表A1，负荷及线路阻抗幅值数据来自文献[21-22]。

图4 初始网络拓扑结构Fig.4 Topology of initial network

基本参数设置如下：投资回报期限n=20年；线路运维费用率γL=0.01；DG单位容量投资为8 000 kV·A；各线路年最大负荷损耗小时数均为3 000 h；DG功率因数均为0.9；系统单位电价为0.55 kW·h；节点电压允许范围为0.95～1.05p.u.。

3.2 规划结果分析

3.2.1 划分集群前后规划结果对比

为了说明考虑集群划分规划方法的优越性，本文构建了2种不同的规划方案。预设DG系统渗透率约束λˉsys=0.9，方案1不进行集群划分，采用上层规划模型进行规划，将10 kV配电系统每个节点视为一个集群；方案2采用本文所提的考虑集群划分的网源协调规划模型进行规划。规划后网络拓扑图及集群划分结果如图5所示，新增DG安装位置及容量如图6所示。

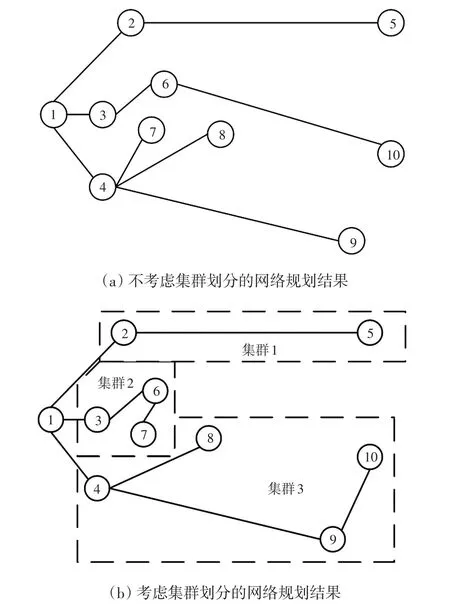
图5 两种方案网络规划结果Fig.5 Network planning results of two schemes

不划分集群时，为了避免DG安装容量因超过节点的最大负荷功率而被削减，DG主要被配置在负荷较大的节点。而划分集群后，由于允许集群作为反向功率流通范围，集群内各节点DG安装容量可能会超过该节点的最大负荷功率，多余的出力将会被外送到该集群内其他DG安装容量较小的节点。

图6 新增DG安装位置与容量Fig.6 Installation locations and capacities of added DGs

由表1可知，方案1分布式电源的出力削减比例高于方案2，而渗透率低于方案2。这是由于不划分集群时不允许各节点功率倒送至电网，对于DG出力大于节点最大负荷功率的部分直接进行削减；而划分集群后由于允许集群内部的功率交互，提高了集群内源荷匹配水平，增大了DG系统渗透率。

由表1可以看出方案2的投资、运维费用对比方案1均有下降，结合图5的规划结果可知集群划分的引入改变了网络拓扑结构，使得规划后的线路路径更加合理。方案2相比于方案1，网损费用减少近14%，购电费用减少近21%，可以看出集群划分有助于减少网损，降低系统流入配电网的电量，验证了集群规划可以提高DG消纳能力的结论。方案1年综合费用为478.502万元，方案2年综合费用为424.754万元，可见集群划分的引入为配电网网源协调扩展规划带来了显著的经济效益。

表1 方案1、2规划结果Tab.1 Planning results of schemes 1 and 2

3.2.2 集群划分与网源变化的动态调整

为了体现本文所提规划模型中集群划分对网源变化的动态适应，本文获取了3种下层集群划分情形，对比分析不同情况下集群划分对网源变化的匹配问题。其中情形A为对前述方案1所得网络拓扑结构与DG配置使用下层模型进行集群划分；情形B为选取双层优化模型混合遗传算法中间结果；情形C为方案2最终集群划分结果。不同情形下集群划分结果与指标值如表2所示。

表2 集群划分结果Tab.2 Result of cluster partition

由表2可知，在不同的网络拓扑结构与DG配置情况下，下层模型均能得出划分结果，且3种情形下节点划分结果结构性与功能性表现良好，未出现孤立节点。对比情形A与情形C，可以看出方案2集群划分结果模块度指标优于方案1，说明划分增强了节点间的结构强度与电气耦合程度；方案2有功平衡度指标优于方案1，说明集群划分充分发挥了群内各节点特性之间的互补，进一步验证了集群划分对于DG消纳能力的提升。

3.2.3 DG渗透率对规划结果的影响

式（10）是对DG系统渗透率的约束，给定的系统渗透率上限不同会对规划结果产生影响。将方案1与方案2分别在设定不同的系统渗透率限制下进行规划，得到的结果如图7所示。由规划结果可知，在不同的系统渗透率约束下，方案2的年综合费用均小于方案1，说明考虑集群划分的规划方法在大规模DG接入情况下均具有良好的经济效益；随着系统渗透率的上升，规划总成本整体呈下降趋势，这是由于系统渗透率上升后大部分负荷功率由安装的DG提供，向上级电网购电成本大幅度降低。

图7 不同DG系统渗透率时的总成本现值Fig.7 Present value of total cost with different system permeabilities of DG

表3 方案3、4规划结果Tab.3 Planning results of schemes 3 and 4

4 结论

本文分析了分布式电源高渗透率接入情况下配电网面临的问题，提出一种考虑集群划分的网源协调扩展规划模型，重点解决集群划分与配电网络变化的动态适应问题，采用分层交互迭代策略，以基于改进遗传算法的混合智能优化算法求解。结果分析表明：

（1）考虑集群划分后的投资、运维、网损费用有所减小，网络拓扑结构及线路布局更加合理；

（2）考虑集群划分的网源协调规划使DG容量规划在各节点的分布更加合理，降低电源出力削减比例，提高了DG渗透率；

（3）所提模型保证了集群良好的结构性，提高了群内节点互补能力，同时使得考虑集群划分的配网规划可以适应网络拓扑结构与DG配置的动态变化；

（4）DG渗透率上限值对DG和网络规划均有影响。

附录A

表A1 支路参数Tab.A1 Branch parameters