楔形撞头作用下固支矩形板的耐撞性

黄 东，郭 翔，董 斌，李元泰，贺梦豪

（武汉第二船舶设计研究所，武汉430064）

0 引 言

船舶碰撞事件时有发生，如油船“桑吉”轮与散货船“长峰水晶”轮在长江口以东约160 海里处发生碰撞。一旦船舶发生严重碰撞，船员和乘客的人身安全受到严重威胁，同时造成的环境污染和经济损失均难以预估。因此，研究人员对船舶的抗碰撞能力进行了大量研究。胡志强等[1]概述了船舶碰撞与触底事故研究进展，且阐明了船舶碰撞内部力学机理是研究构件损伤和变形模式等。其中，船体构件损伤和变形模式与撞击船船首形状密切相关。

为了快速预报船体结构的耐撞性能，简化理论分析方法受到了研究人员的关注。Wang 等[2]采用刚塑性理论以及虚功原理，研究球形撞头作用下固支圆板的大塑性变形，将固支圆板的变形模式假定为球面与圆锥面相结合的形式，导出了固支圆板的接触反力-横向变形的关系式；Gong 等[3]详细讨论了球形撞头作用下固支圆板的大塑性变形，根据模型试验结果假设固支圆板的变形模式由三部分组成：与撞头相接触的区域具有球面的形状，与球面相邻的是抛物面，而靠近固支边界的部分则具有对数曲面的形式，导出了撞击力-横向变形的关系式；Shen[4]同样研究了球锥形撞头作用下固支圆板的耐撞性。庄科挺等[5]和黄东等[6]分析了球形撞头作用下的固支矩形加筋板的力学性能。

楔形撞头作用下固支矩形板的耐撞性能分析，也是船舶结构耐撞性分析中最为基础性的研究课题之一，一直受到足够的重视。Shen 等[7]结合楔形撞头冲击矩形板试验结果，通过简化矩形板的变形模式提出了一种理论方法，对楔形撞头作用下固支矩形薄板做出合理的断裂预报，经研究发现，极限冲击能量与矩形板的厚度有密切的联系；Sun等[8]将前倾型船艏视为刚性楔形撞头，将被撞船的舷侧结构简化成双层夹层板结构，以研究楔形船艏撞击下被撞船双层舷侧的耐撞性能；杨树涛[9]结合楔形撞头撞击矩形加筋板试验，简化矩形加筋板的变形模态，推导了矩形加筋板的变形能公式。

为进一步研究楔形撞头作用下固支矩形板的耐撞性，基于刚塑性理论，本文提出了一种新的简化理论方法，简化了固支矩形板的变形模式，这种方法能准确地描述固支矩形板的变形模式。本文的分析限于低速撞击的情况，从而可简化为准静态问题处理[10]。

1 简化理论分析方法

图1 给出了楔形撞头作用下固支矩形板有限变形分析的示意图。假定固支刚塑性矩形板的边长分别为2a0和2b0，厚度为t。位于矩形板的中央，承受楔形刚性撞头的作用。

如图1 所示，假定固支矩形板的有限变形由两个对称的板块①和两个对称的板块②组成，单个板块①为梯形，单个板块②为三角形，均具有抛物曲面的变形模式。固支矩形板为对称结构，故以X 轴、Y 轴正半轴方向的板块为例，固支矩形板有限变形的变形模式具有下述的形式。

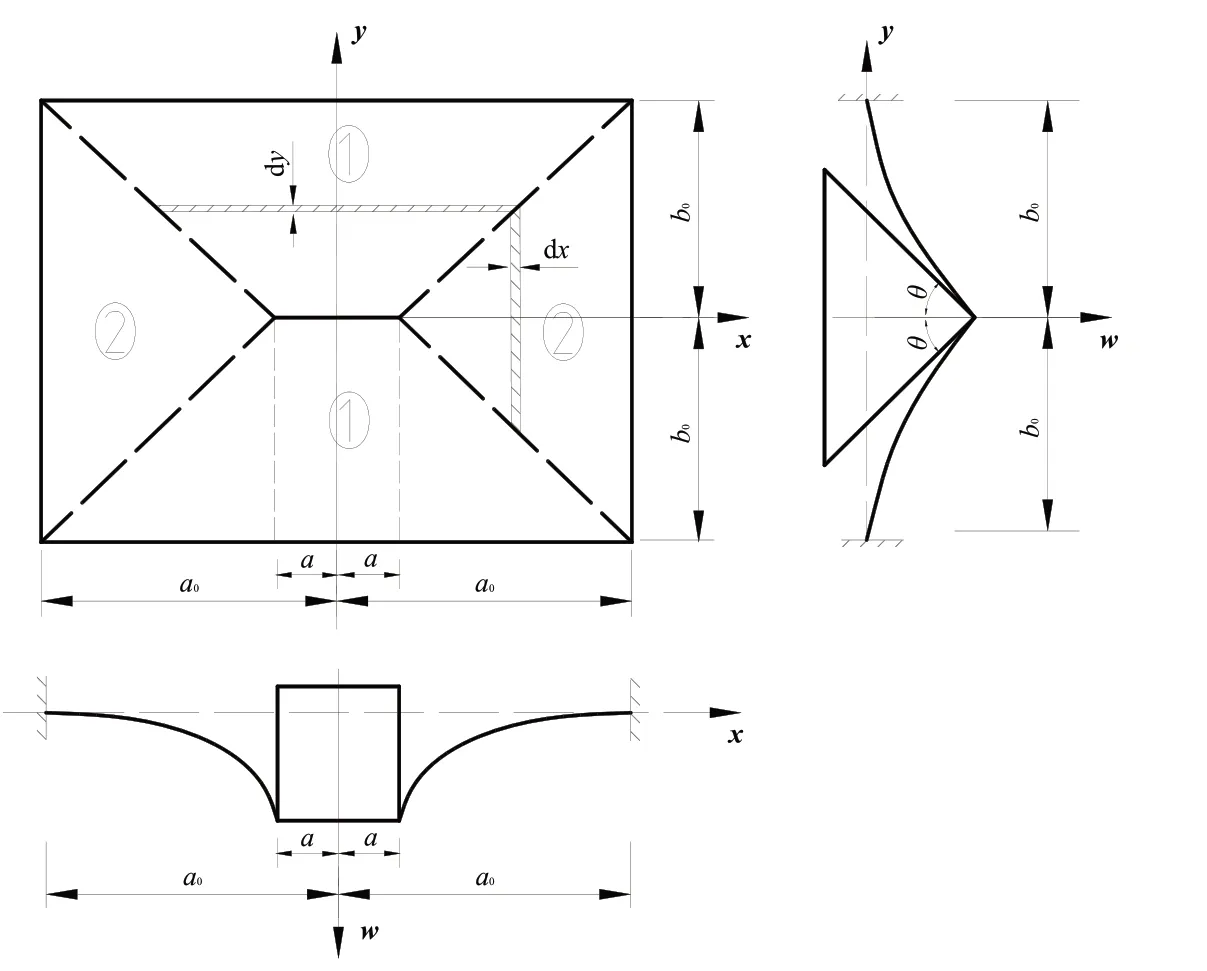
图1 固支矩形板有限变形的变形模式Fig.1 The finite deformation mode of the clamped rectangular plate

1.1 板块①的有限变形近似表达式

假设板块①变形模式表达式为

板块①的边界条件为

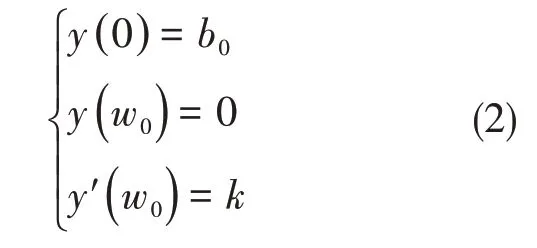
系数C1、C2和C3由边界条件确定，由此得到y表达式为

经整理得到板块①挠度w1表达式为

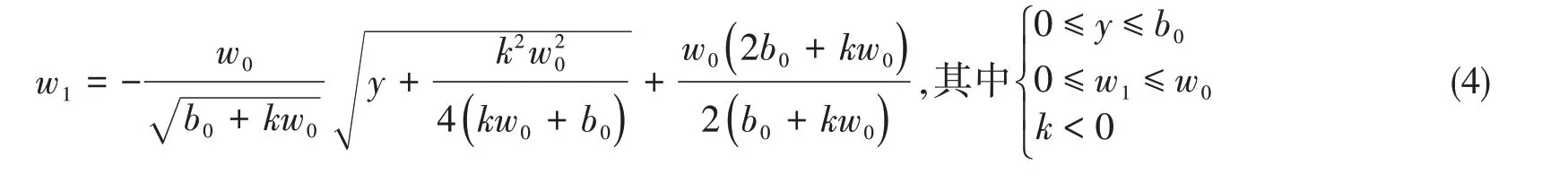
式中，b0为矩形板半宽，K = 1/k为楔形撞头的斜率，w0为最大横向变形。

1.2 板块②的有限变形近似表达式

假设板块②变形模式表达式为

板块②的边界条件为

系数C1、C2和C3由边界条件确定，由此得到x表达式为

经整理得到板块②挠度w2表达式为

式中：a0为矩形板半长，a为撞头半长，w0为最大横向变形。

在本文的分析中，楔形撞头作用下固支矩形板的变形将人为地划分成对称的两个部分。分别计算出各自的撞击力与最大横向变形之间的关系式，在此基础上采用文献[11]提出的叠加方法，最终得到固支矩形板总的撞击力与中点横向变形之间的关系曲线。分析中仅仅考虑了伸长应变εx和εy对固支矩形板耐撞性能的作用，忽略了剪切以及弯曲应变的影响。

2 楔形撞头与固支矩形板之间的撞击力

2.1 板块①的变形计算

已知固支矩形板有限变形的表达式，便可分别列出固支矩形板总体变形的虚功表达式，并导出板块①变形情况下撞击力P1与其横向变形w0之间的关系式。

板块①的中面伸长应变εy的表达式为

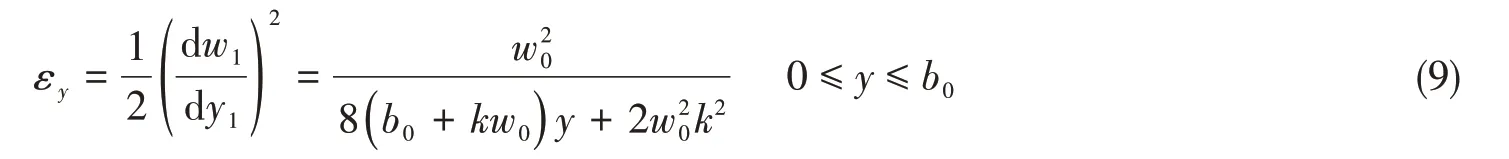
伸长应变εy的变分表达式为

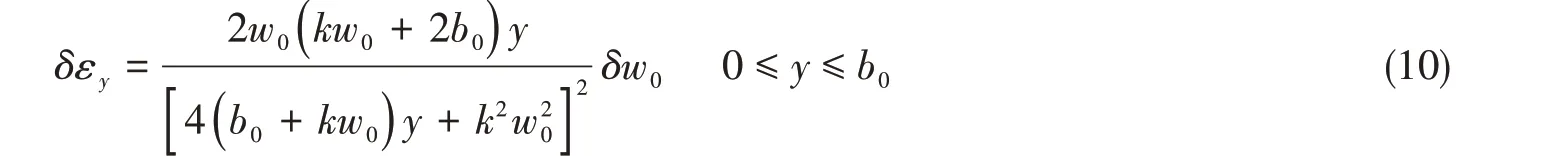
为了导出总体变形情况下板块①的撞击力P1与其横向变形w0之间的关系式，列出固支板块①的虚功表达式为

将公式（10）代入上述公式（11）。为简化公式，令λ = b0+ kw0，β = k2w20，经整理后得到

其中，a0为矩形板半长，b0为矩形板半宽，w0为最大横向变形，a 为撞头半长，1/k 为楔形撞头的斜率，t为矩形板厚度，σ0为材料塑性流动应力。

2.2 板块②的变形计算

已知固支矩形板有限变形的表达式，便可分别列出固支矩形板总体变形的虚功表达式，并导出板块②变形情况下撞击力P2与其横向变形w0之间的关系式。板块②的中面伸长应变εx的表达式为

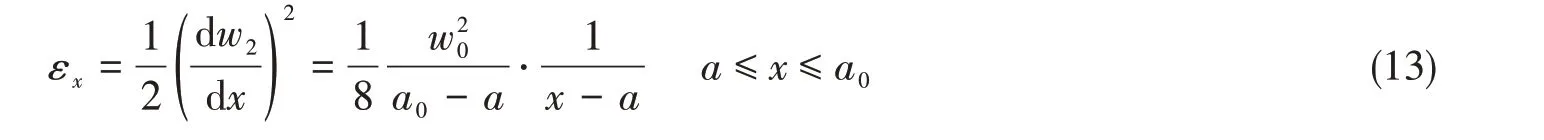
伸长应变εx的变分表达式为

为了导出板块②的撞击力P2与其横向变形w0之间的关系式，列出固支板块②的虚功表达式为

将公式（14）代入上述公式（15）中，经整理后得到

式中，a为撞头半长，a0为矩形板半长，b0为矩形板半宽，w0为最大横向变形，t为矩形板厚度，σ0为材料塑性流动应力。

2.3 楔形撞头与矩形板的之间的总撞击力

如图1所示，矩形板被划分为两个对称的板块①和两个对称的板块②。故矩形板的总撞击力P为

3 实例计算

3.1 实例验算

根据Zhang 等[12]完成的9 组楔形撞头撞击矩形板试验，撞头的顶角为2θ=90°，矩形板厚度t=1.455 mm，其材料属性如表1 所示。矩形板材料的塑性流动应力σ0=0.5×( σs+ σb)[3]。

根据公式（12）、（16）和公式（17）分别计算板块①、板块②以及整个矩形板的撞击力P1、P2和P。矩形板初始断裂的试验数据和简化理论分析方法计算结果如表2所示。

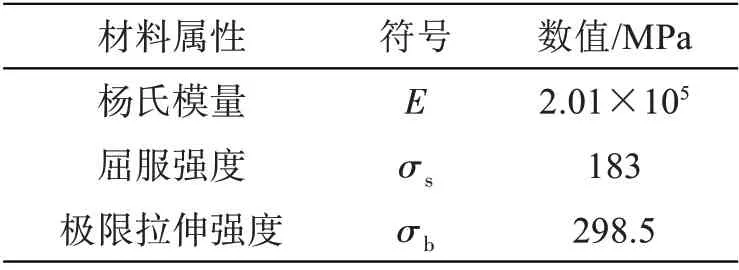
表1 矩形板的材料属性Tab.1 Mechanical properties of material of the rectangular plate

表2 试验数据与理论计算结果Tab.2 Summary of experimental results and the calculation results of simplified analysis method

据表2可知，当撞头尺寸2a=80 mm 时，简化理论方法的计算误差均未超过20%；当撞头尺寸2a增加时，简化理论方法的计算误差随之增加；当b0/a0=1.5 或者a0/b0=1.5 时，简化理论方法的计算误差较b0/a0=1时均有所增加。

3.2 误差分析

分析计算结果发现，简化理论方法的预报值大于试验值，且当撞头尺寸2a增加时，简化理论方法的计算误差随之增加。究其原因，分析如下：

（1）误差来源分析

在假设固支矩形板的变形模式时，为保证矩形板变形的连续性，将板块①以及板块②的变形模式均假定为抛物线变形模式；而矩形板的真实变形情况是，板块②的真实变形曲率较大，接近假定的抛物线变形模式，板块①的真实变形曲率略小，与假定的抛物线变形模式稍有误差。文献[12]中矩形板试验模型B2的真实变形三维扫描图可证实上述分析，如图2所示。因此，对板块①的理论预报值是主要误差来源。

（2）误差增大分析

其一，理论预报值大于试验值的原因：根据公式（9）可知，变形曲率越大则拉伸应变越大，而假定板块①为抛物线变形模式的变形曲率略大于真实情况，故导致理论预报值撞击力P1偏大。

其二，计算误差增大的原因：当撞头尺寸2a增加时，板块①的变形区域随之扩大，相当于扩大了主要误差源，故使得误差进一步增加。所以，随着撞头尺寸2a的增加，最终导致理论预报值更高于试验值。

图2 模型B2矩形板真实变形的三维扫面图（Zhang[12]）Fig.2 The 3D scanning map of the actual deformation of the test B2（Zhang[12]）

4 结 论

本文为预报楔形撞头作用下固支矩形板的耐撞性，提出了一种新的简化理论分析方法，通过与试验结果对比，得到如下结论：

（1）采用了抛物曲面的变形模式的设定，该变形模式较为正确地描述了矩形板变形形状的分布规律，为固支矩形板的耐撞性分析奠定了良好的基础；

（2）当楔形撞头长度2a=80 mm 时，简化理论方法的计算误差均未超过20%，故该方法能够达到准确预报的要求；

（3）撞头尺寸与矩形板边长之比a/a0减小时，简化理论方法的计算误差随之减小。故撞头尺寸较小时，该方法能够更加准确地预报固支矩形板的耐撞性；

（4）矩形板的长宽比b0/a0=1时，简化理论方法的计算误差最小。故楔形撞头撞击固支方板时，该方法能够更加准确地预报固支板的耐撞性；

本文的研究成果不仅仅局限于楔形撞头作用下固支矩形板的耐撞性预报，同样为球形撞头撞击固支矩形板或固支圆板提供了有意义的参考。