基于压缩蠕变试验的观察窗蠕变特性研究

陈 薇，屈 平，张爱锋

（中国船舶科学研究中心，江苏无锡214082）

0 引 言

有机玻璃作为深海耐压结构观察窗的常用材料，其主要优点[1]包括材料的物理性能再现性好、结构破坏前形变明显、具有大量裂纹的破坏预警、材料制备技术成熟，以及加工难度低等。观察窗是深海耐压结构的一部分，需要长期在较高的静水压力下持续工作，而作为典型的粘弹性材料，有机玻璃在室温高压环境中会产生不容忽视的蠕变变形，因此，其在深海工况中的压缩蠕变特性值得关注。

董自虎等[2]根据四种常见船用吸声材料和浮体材料的压缩蠕变试验数据，建立了描述船用高分子材料压缩蠕变特性的粘弹性材料Burgers 模型；刘伟等[3]针对MDYB-3 有机玻璃进行了蠕变行为温度效应的研究，且将蠕变三个阶段分别以陈化理论、Norton 公式和指数公式进行了描述。张志林[4]通过单轴拉伸蠕变断裂试验得到YB-3 有机玻璃的拉伸蠕变拟合曲线和不同拉应力作用下的蠕变断裂应变和断裂时间；田常录等[5]提出了应用塑性力学全量理论的深海耐压结构观察窗蠕变变形理论分析方法；刘道启等[6]开展了对深潜器主、侧观察窗分别保压6 h和9 h的试验研究，以探究观察窗结构的蠕变特性；廉俊盛[7]采用ANSYS蠕变分析方法模拟文献[6]的观察窗蠕变试验，并进行了结果对比。国内现有关于观察窗蠕变的研究大多直接采用航空有机玻璃的拉伸蠕变本构方程，但航空有机玻璃与深海耐压结构有机玻璃的工况差异较大且有机玻璃材料的拉压性能并不相同。因此，有必要开展针对深海耐压结构工况的有机玻璃蠕变特性研究。

本文通过有机玻璃试样的室温单轴压缩蠕变试验，选择合适的蠕变本构方程并拟合出蠕变参数，探究有机玻璃材料的常温压缩蠕变特征。然后基于试验得到的本构方程，建立ANSYS 模型模拟平圆形、锥台形和球扇形观察窗的蠕变变形，探究不同形式观察窗的蠕变特征。

1 蠕变试验

1.1 试验简介

有机玻璃单轴压缩蠕变采用图1 所示的等截面圆柱体试样，选取锦西化工研究院提供的YB-3有机玻璃块，通过机加工制备而成。试样制备和检查均参考GB/T 1041-2008《塑料压缩性能的测定》进行。

分别在室温（10℃～35℃）环境中进行20 MPa、30 MPa 和40 MPa 三组应力水平下的蠕变试验。试验加载和保压由恒压自动跟踪泵完成，加载速率为7 MPa/min，保压时间约36 d，试验过程中的温度、压力、位移数据通过数据采集系统进行记录。试验温度变化曲线如图2 所示，可以看出，试验时间内虽存在一定温差，但仍在室温范围内。

图1 有机玻璃压缩蠕变试验试样Fig.1 PMMA specimen for compression creep test

1.2 试验结果

根据试验数据绘制蠕变曲线如图3所示，试验时间内试样的蠕变曲线呈现较大的波动性，但整体曲线表现出蠕变应变率随着时间增长而逐渐减小的趋势，基本符合蠕变的第一阶段特征，尚未进入蠕变第二阶段。

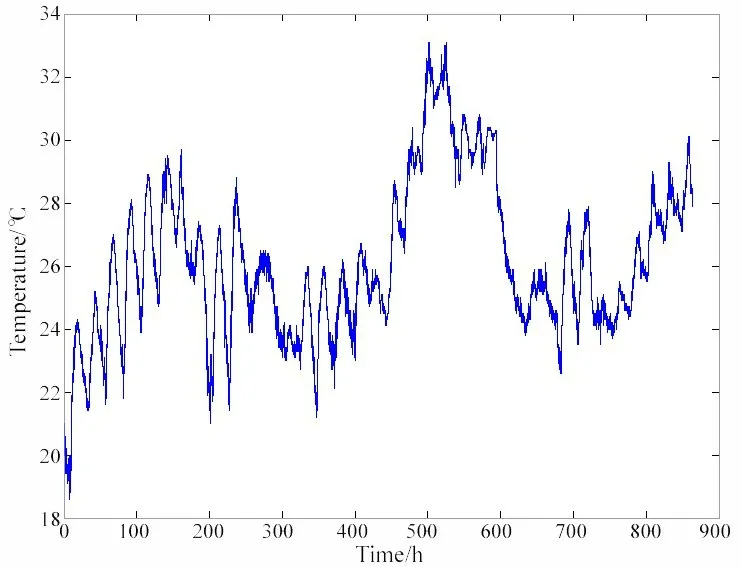
图2 环境温度曲线Fig.2 Curve of environmental temperature

图3 有机玻璃试件压缩蠕变曲线Fig.3 Creep curve of PMMA specimens

因加载时间较短，故可忽略加载过程中的蠕变作用，提取加载结束时的试样应变值记作弹性应变。同时分别提取三组试样的其它蠕变特征参数，包括总应变、蠕变应变和蠕变时间，具体数据如表1所示。可以看出：（1）保压36 d 后，三组应力水平下的蠕变应变均占总应变的1/3 以上，不容忽略；（2）应力大小和保压时间对有机玻璃的蠕变有显著影响，有机玻璃的蠕变速率随着外加应力的增大而增加，蠕变量随着时间的增长而增加。

表1 试样压缩蠕变数据汇总Tab.1 Data of compression creep test

2 蠕变本构方程

2.1 含温度修正的陈化理论

由于原始数据的波动不利于蠕变本构方程和拟合蠕变参数的选择，因此需要考虑对原数据进行修正。图4截取了30 MPa压力作用下有机玻璃试样前250 h的蠕变应变-温度-时间关系曲线，如图所示，两条曲线的波峰基本对应，蠕变应变对于温度变化的响应略有滞后。由此可认为，室温范围内有机玻璃蠕变曲线与温度变化有着明显的相关性。

已知温度对有机玻璃材料的密度、模量和蠕变速率均有一定影响，由于本次试验数据有限，各因素的影响权重尚无法确定，因此可引入温度修正函数，基于唯象理论对试验结果进行拟合分析。

受应力和温度影响的蠕变曲线在第一阶段通常存在几何相似性[8]，因此对变温下的蠕变规律进行一般简化处理，即将蠕变应变表示为应力σ、时间t和绝对温度T的独立函数的乘积，

图4 蠕变应变-温度-时间曲线（30 MPa）Fig.4 Curve of creep strain,temperature and time under a pressure of 30 MPa

引用陈化理论

式中，A、m、n为材料常数，由蠕变试验确定。

结合式（1）和式（2）得到含温度修正函数的陈化理论

式中：e-k/T为简化后的温度修正函数；T为绝对温度，K；k由蠕变试验确定。

将式（3）等号两边同时取对数可得

式中，εc、σ、t和T 为试验记录的数据。代入试验数据，在Matlab 软件采用最小二乘法即可拟合出待定系数，如表2所示。

表2 含温度修正的陈化理论蠕变本构方程拟合系数表Tab.2 Coefficients of creep constitutive equation of accumulation theory with temperature revision

拟合相关度为0.986 4，拟合效果良好。

将表2 中的系数代入式（4），等号两边同时求e的指数，即可得到有机玻璃压缩蠕变第一阶段的本构方程：

式中：εc为蠕变应变，%；σ 为应力水平，MPa；t 为蠕变时间，h。

图5 给出了参考温度为25 ℃时，有机玻璃的蠕变拟合曲线。拟合曲线与试验数据各应力水平的蠕变应变整体变化趋势一致，曲线吻合度较好。

2.2 压缩蠕变试验的有限元模拟

由于结构与载荷均具有轴对称性，可采用二维1/2 轴对称建模以减小计算量，模型宽为15 mm，高为60 mm，采用plane182 单元，单元网格尺寸为1 mm。有机玻璃杨氏模量取试验测得的平均值2 729.5 MPa，泊松比为0.35。在模型对称轴处施加水平位移约束，对底部施加轴向位移约束（图6）。分别在模型顶部施加20 MPa、30 MPa和40 MPa垂直向下的均布压力载荷；导入图2的环境温度数据，对模型施加变化温度载荷。采用隐式蠕变方法，选择TBOPT=6所对应的初始蠕变方程，根据式（5）输入C1～C4参数。采用大变形静力分析求解，求解时间为864 h，步长设置为4 320步。

根据有限元模拟结果绘制蠕变曲线，如图7所示。可以看出，有限元解与试验值的蠕变曲线图像基本吻合，整体变化趋势一致，由此说明，式（5）能较好地描述该温度范围中YB-3 有机玻璃的单轴压缩蠕变过程。由于有限元蠕变分析仅考虑了温度对蠕变速率的影响，忽略了温度对材料密度和模量的影响，因此该模拟蠕变曲线并没有出现实际试验中的波动。

图5 拟合结果与试验数据对比图（25 ℃）Fig.5 Comparison between fitting curve and test data

图6 试样模型及网格划分Fig.6 FEM model of PMMA specimen

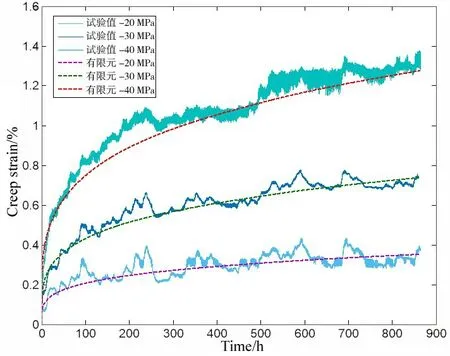
图7 试样有限元模拟蠕变曲线Fig.7 FEM simulated creep curve of PMMA specimen

3 不同形式观察窗的蠕变特征

3.1 有限元建模

分别设计平圆形、锥台形和球扇形观察窗模型，如图8 所示。窗口开口直径均为100 mm，厚度均为50 mm，锥台形和球扇形观察窗的锥形夹角均为90°,平圆形观察窗最大直径为160 mm。建立二维1/2 轴对称建模，采用plane182 单元，单元网格尺寸为1 mm，材料参数及蠕变方程设置同2.2 节。分别在观察窗上表面施加15.6 MPa 垂直于表面的均布压力载荷，设置温度载荷为25 ℃，在模型对称轴处施加对称位移约束，对窗座施加固定位移约束。窗座为钛合金结构，其杨氏模量远大于观察窗，因此将窗座设为目标面，将观察窗设为接触面，分别使用TARGE169 和CONTA172 单元建立接触对，采用ANSYS的面-面接触分析，接触容差设置为0.1，接触面摩擦系数为0.1，其余参数默认。设置大变形静力分析求解，蠕变分析求解时间为864 h，步长为4 320步。

图8 锥台形、平圆形和球扇形观察窗模型的主要设计参数Fig.8 Design of conical frustum viewport,flat disk viewport and spherical sector viewport

3.2 结果分析

利用ANSYS 蠕变分析进行求解后，输出直接加载、保压24 h和保压864 h三个时刻各模型的主要蠕变参数如表3所示，其中结构的整体变形程度由最大轴向位移表征。

表3 观察窗模型的主要蠕变参数Tab.3 Main parameters of creep characteristics of viewport models

可以看出：（1）保压过程中，由于材料发生蠕变，三种观察窗的结构变形程度均有加大，仅保压24 h，最大轴向位移值就已经增加了15%以上，可见观察窗受压状态下的蠕变现象不容忽视；（2）保压前期蠕变速率较快，因此近一半的蠕变位移产生于保压前24 h 内；（3）由于锥台形和球扇形观察窗的窗座设计允许窗户与窗座在接触面产生相对滑动，因此锥台形和球扇形观察窗结构在直接加载和保压过程中的轴向位移均大于平圆形观察窗；（4）蠕变会导致锥台形和球扇形观察窗与窗座的相对滑动进一步增大，因此在保压过程中，锥台形和球扇形观察窗的位移蠕变比始终高于平圆形观察窗；（5）锥台形观察窗在直接加载时的最大等效应力明显高于另两种观察窗，说明锥台形结构的应力集中现象最为严重，因而锥台形观察窗应力集中处的蠕变变形也更大；（6）保压过程中，三种观察窗的最大等效应力均有所减小，即在保压过程中，随着结构的持续变形，应力集中现象有所缓解。

输出三个观察窗模型蠕变过程中的节点云图结果如图9～11所示，其中（a）组为平圆形、锥台形和球扇形观察窗在直接加载至设定压力时（蠕变开始前）的等效应力云图，（b）组和（c）组分别为三个模型蠕变864 h后的等效应力云图和等效应变云图。

图9 平圆形观察窗的结果云图Fig.9 Contour plot of flat disk viewport

图10 锥台形观察窗的结果云图Fig.10 Contour plot of conical frustum viewport

图11 球扇形观察窗的结果云图Fig.11 Contour plot of spherical sector viewport

对比图9～11 的（a）组和（b）组可以发现，保压过程中，各形式观察窗内部的应力分布规律基本不变。由图9～11 的（c）组可以看出：（1）平圆形观察窗在窗座边缘沿线的蠕变变形较大，下表面区域的径向拉伸变形因蠕变而有所增加；（2）锥台形观察窗的蠕变变形主要发生在小端面边缘应力集中区域；（3）球扇形观察窗的蠕变应变近似地呈现为沿球壳径向从内至外的阶梯式递减分布；在直接加载和保压过程的模拟中，锥台形观察窗和球扇形观察窗结构内部的主要应变始终为压应变，而平圆形观察窗下端出现拉应变且应变量因蠕变变形而逐渐增加；由于有机玻璃材料的抗拉强度大大低于抗压强度且断裂延伸率较低[9]，因此蠕变变形会对平圆形观察窗的结构强度产生不利影响。

4 结 语

本文设计并开展了YB-3 有机玻璃试样的室温单轴压缩蠕变试验，发现保压36 d 过程中，有机玻璃在室温高压环境中的蠕变处于蠕变第一阶段。通过引入温度函数对试验数据进行修正，选择陈化理论公式，采用最小二乘法拟合出YB-3 有机玻璃的压缩蠕变本构方程。基于该本构方程，建立AN⁃SYS 试样模型进行求解并与试验值进行对比，证明了该本构方程具有一定的准确性。最后运用有限元模拟探究了不同观察窗的蠕变特征，可为深海耐压结构有机玻璃观察窗的蠕变研究和工程设计提供参考依据。