基于Modelica语言的ROV力学系统建模与仿真
韩 枫,谢基榕
(中国船舶科学研究中心深海空间站研究设计部,江苏无锡214082)
0 引 言
在ROV 的运动建模过程中,存在较强的非线性特性,且不同自由度间的耦合作用十分明显,尤其是水动力学部分。传统Simulink 建模方式本质上仍是确立系统的输入输出量后,将系统的微分代数方程推导为状态空间表达式,以确定的因果运算机制建立并求解仿真模型。当涉及此类多变量、非线性与多耦合的复杂系统建模时,采用此方式需花费大量时间进行因果赋值运算。与之相比,Modelica语言具有非因果建模特性,即声明方程时不限定方程求解方向,可极大简化建模工作量。
本文依据Fossen提出的针对一般水下航行器的运动建模理论[1]并应用Modelica建模语言,以ROV力学系统为例,提出一种通用的、面向对象的水下航行器运动建模方法;对ROV 进行动力学、运动学分析,对于流体动力部分针对其运动特性单独阐述、简化;应用Modelica 语言面向对象特性,划分系统仿真框架如图1所示,在基于该语言的MWorks平台内,形成ROV动力学、运动学子系统下各模块由受力模型到仿真模型转化,通过组件实例化与基类继承的方式实现模型重用,创建ROV 力学系统。最后,将推进器动态性能仿真应用至ROV 斜航与下潜仿真工况中,对仿真结果进行分析,以展示建模方法的合理性、快捷性。
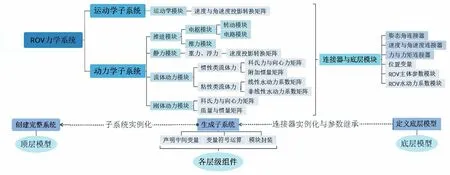
图1 仿真框架与系统层级划分Fig.1 Simulation framework and system hierarchy division
1 Modelica语言特性
Modelica 是一种面向对象、采用非因果建模与陈述式建模的多领域物理系统建模语言,可应用于几乎所有工程领域[2]。该语言采用基于方程的方法描述真实物理系统,其内置的Modelica标准库包含了机、电、液、热、控等多领域的基础组件模型,可实现对现代复杂工程系统进行整体性能分析与评估的任务。
Modelica 语言应用面向对象的思想[3],支持采用分层机制、组件连接机制和继承机制构建模型[4],可简化模型结构的复杂程度。不同于Simulink 建模需要将数学模型推导为因果关系明确、数据流向恒定的状态方程,该语言采用方程定义变量的行为,无需人为划分方程求解方向,求解器根据给定条件自行求解未知量。该语言可根据系统的真实物理拓扑结构进行建模,其组件视图具有与真实系统相似的结构层次与布局。
2 水下航行器运动学建模
采用ITTC 推荐坐标体系描述水下航行器六自由度运动,如图2 所示。使用欧拉角法描述航行器姿态角[5],航行器位置和姿态矢量表述为
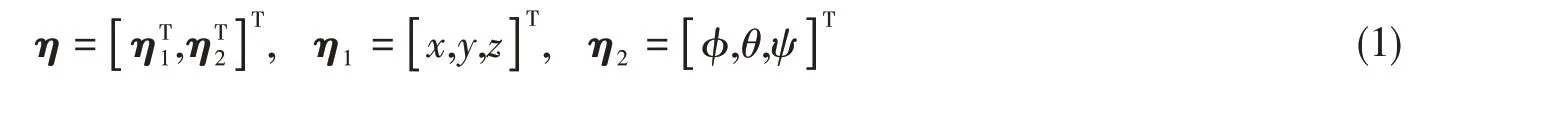
航行器速度与角速度矢量在动系中投影为

利用刚体有限转动理论和欧拉旋转定理[5],可推导速度、角速度从其在动系中投影v到其在定系中投影η˙的转换矩阵J1(η2)、J2(η2),两者共同构成水下航行器运动学转换矩阵J(η2):
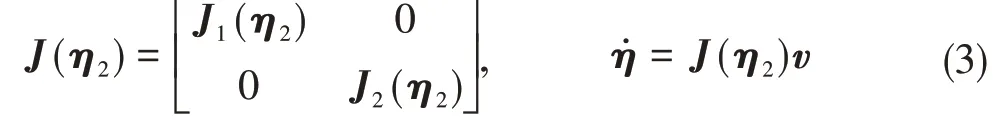

图2 水下航行器定系与动系定义Fig.2 Definition of fixed and moving coordinate system of underwater vehicle
3 水下航行器动力学建模
将航行器所受外力(矩)划分为惯性力-τ、流体动力τH、静力τR、推力τP、外界干扰f 等部分,建立动系内动力学平衡方程:

式中各项皆为六行列矢量,列矢量的前三行、后三行元素分别表示该力、该力矩在动系中的投影。
3.1 刚体动力学建模
将航行器视为刚体,对动系原点应用动量定理与动量矩定理,可得到刚体动力τ矢量形式:

式中,MRB是航行器对动系原点的刚体质量与惯性张量矩阵;CRB是由航行器绕动系旋转引起的科里奥利力与向心力矩阵。根据达朗贝尔原理,动系作为非惯性系,在其中进行受力分析时,需将刚体动力取负值-τ,作为惯性力参与到平衡方程的求解中。
3.2 流体动力学建模
将航行器所受流体动力τH划分为与加速度v˙相关的惯性力τA和与速度v相关的粘性力τD。将惯性类流体力τA按附加惯量矩阵MA和由MA引起的科氏力和向心力矩阵CA的形式分离为

由ROV的对称性假设,可将其附加惯量矩阵MA中非对角线元素消去,矩阵CA亦受到简化。
将航行器所受粘性类流体力τD分离为

式中,D为水动力阻尼矩阵,可将其分解为线性、非线性水动力阻尼矩阵DL、DNL两项:

由ROV 对称性假设,且其大部分运动皆在水平面与垂直面内进行,运动速度一般为低速,可忽略其水动力阻尼的耦合效应,视粘性水动力系数为相互独立,并忽略二阶以上水动力系数的影响。
航行器受洋流U 作用时,先于定系中描述洋流速度与角速度投影vU,再于动系中利用转换矩阵J(η2)-1求其投影vtransU并计算航行器相对洋流的速度与角速度投影vr,其结果用于计算流体动力τH。
3.3 静力学建模
航行器受静力τR作用,包括重力G、浮力B 和浮心位置rB的影响,需先计算静力于定系中垂向投影,再利用速度投影转换矩阵的逆阵J1(η2)-1求取其于动系中投影,由浮心位置rB计算恢复力矩。
3.4 推进系统建模
推进系统模型可划分为电枢模型与推力模型,前者用于计算外部电压作用下电机输出转速,经推力系数、转矩系数拟合后,可求得标量形式表述的螺旋桨轴向推力与轴向转矩;后者则定义螺旋桨位置和角度,从而获知轴向推力及转矩、推力在质心处转矩的矢量形式,并求其在动系内投影。
对推进系统中直流电机的电枢部分进行建模,其简化模型组件视图如图3所示。列写其回路电压平衡方程与转轴转矩平衡方程:
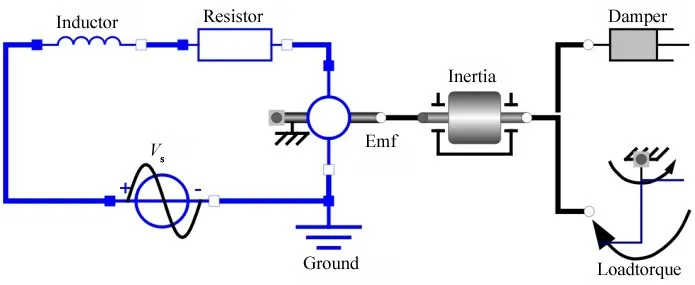
图3 电枢模块组件视图Fig.3 Components of armature module

式中,R、L、i 分别是电枢电路中电阻、电感与电流,Vs为输入电压,E 为反电动势E = Ceω,Ce为反电动势系数,ω 为电机转动角速度;fm为电机转轴粘性摩擦系数,Mm为电磁转矩,Mm= Cmi,Cm为转矩系数,Q为螺旋桨切割水流引起负载转矩,Jm为电机与负载折合至转轴的总转动惯量。工程应用中因摩擦系数fm较小可将其忽略,消去中间变量i、E、Mm后,得到以角速度ω 为输出,以电压Vs和负载转矩Q 为输入的直流电机微分方程;在零初始条件下对其进行拉氏变换,根据线性叠加原理,可分别求得Vs与Q到ω的传递函数:
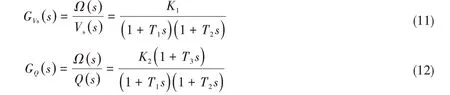
式中,Ki(i=1,2)为增益常数,Ti(i=1,2,3)为时间常数,均为电机固有参数。可联立以推力系数KT、转矩系数KQ表述的推力T 及负载转矩Q方程:

式中,n、D分别为螺旋桨转速、直径。
已知第i 个推进器相对动系的位置矢量riP与角度θi和Ψi,如图4 所示。获知其轴向推力标量Pi、扭矩标量Qi后,可求取该推进器推力、扭矩、推力矩矢量在动系内投影,对各推进器上述矢量投影求和即得总推力(矩)矢量τP。

图4 单个推进器安装位置与角度Fig.4 Installation position and angle of a single propeller
4 水下航行器通用仿真模型建立
根据已分析的水下航行器运动模型与Modelica 语言面向对象的特征,提出一种通用的水下航行器运动建模方法,以ROV 力学系统为例,将其划分为动力学与运动学两个子系统,共下设五个模块:惯性力模块、流体动力模块、静力模块、推进模块(可进一步划分为电枢模块与推力模块)和运动学模块,各模块关系与功能如图5所示。
应用基于组件的建模方法,定义可重用、包含不同变量类型的多个连接器类,在本文中应用如表1所示。模块内通过连接器实例化方式获取所需变量,模块间则通过连接器互联完成信息传输。
欲创建各力学模块,除定义和获取所需变量外,还需在参数区定义相关的模型参数。由于同一参数可能在不同模块内多次出现,为避免冗余,本文将ROV 物理参数与水动力系数集成后单独创建模块,并通过继承方式将参数传递至各力学模块。
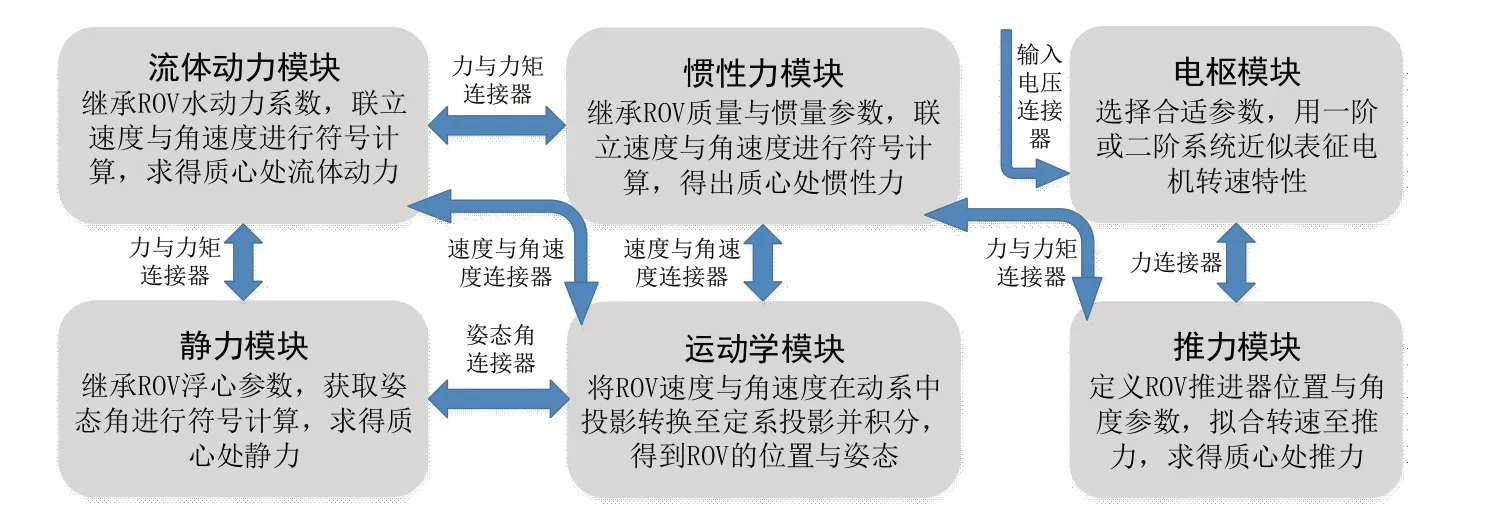
图5 ROV力学系统各模块功能Fig.5 Function of each module of ROV mechanical system

表1 连接器内定义变量类型Tab.1 Variable types defined within the connector
以创建流体动力模块为例,首先在MWorks 平台内定义运动学连接器ROV_ve⁃locity,其中声明速度变量u、v、w 与角速度变量p、q、r,如图6(a)所示;随后建立流体动力模块并继承物理参数模块ROV6dof_parame⁃ters以获取水动力系数,将连接器ROV_veloc⁃ity 实例化为对象p,并创建式(8)中非线性水动力阻尼矩阵DNL,如图6(b)所示。
运用类似方式定义力与力矩连接器实例p1、附加质量矩阵MA、科氏力与向心力矩阵CA、线性水动力阻尼矩阵DL。如图6(c)所示,在equation 块内建立守恒方程,为避免繁琐,用多维数组V 指代速度与角速度变量,利用微分算子der()对时间求导功能计算(角)加速度,由流体动力式(6)~(8)所示,等式左侧取各矩阵变量与(加)速度、角(加)速度变量进行符号运算,等式右侧连接器实例p1内嵌套的力与力矩变量F即为流体动力tau_H。在此模块的图标视图内绘制图像,则流体动力模块封装完毕,可通过内置的运动学与动力学连接器进行模块间信息交互。
运用上述建模方法建立并封装各力学模块,在顶层模型中完成模块实例化,其图标视图如图7所示。对各模块实例的连接器进行匹配,连接器内势变量生成等值的运动学兼容方程,保证了各模块中速度、角速度、姿态角的一致性;连接器内流变量则统一各动力学模块,自动生成如式(4)所示的各受力项之和为零的动力学平衡方程,从而建立起完备的ROV 运动微分方程组。至此完整的ROV 力学系统建立完毕,设定作业工况即可进行仿真。

图6 流体动力模块建立过程Fig.6 Establishment process of hydrodynamic module
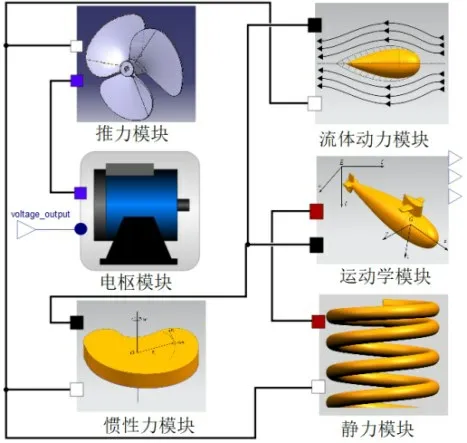
图7 MWorks中ROV力学系统顶层模型视图Fig.7 Top-level model view of ROV mechanical system in Mworks
5 仿真实例
选取文献[6]中ROV 为本文仿真对象,其主体及水动力系数如表2~3 所示,其推进器镜像布置情况如图8 和图9 所示。水平推力T1~T4、垂向推力T9由1002 型推进器产生,垂向推力T5~T8则由1004型推进器产生,前者推力约为后者四倍。

表2 ROV主体物理参数Tab.2 ROV main physical parameters

表3 ROV水动力系数(有量纲)Tab.3 ROV hydrodynamic coefficients(with dimension)
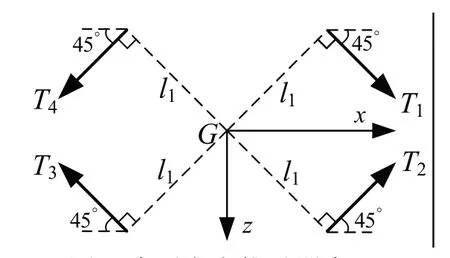
图8 水平方向推进器布置Fig.8 Horizontal thrusters configuration
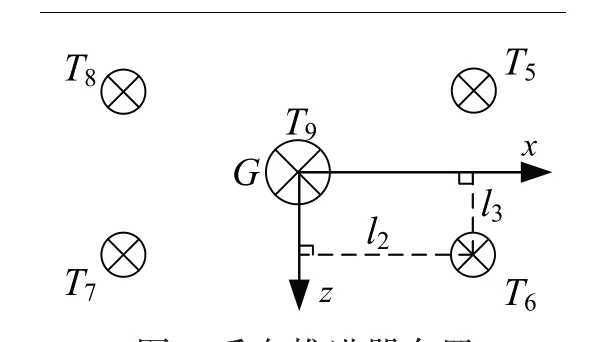
图9 垂向推进器布置Fig.9 Vertical thruster configuration
将推进器输入电压与输出推力进行归一化处理,略去转速生成过程并整合轴向负载转矩影响,使用一阶传递函数拟合推进器正转与反转过程中推力零初始条件下的动态性能,以采用的1002 型推进器[6]动态响应仿真曲线为例,如图10 所示。
设置仿真工况为ROV 在垂直面内做斜航下潜运动,仿真持续时间20 s,应用推进器动态响应仿真结果。垂推始终产生沿垂轴正向的较小合推力,前10 s 内水平推进器满载工作,合推力沿纵轴正向,10 s 后水平推进器断电。ROV 初始速度、姿态角与各推进器推力均为零,全程采用默认Dassl 求解器运算,解出其运动轨迹如图11 所示,其速度、姿态角及所受流体阻力变化过程如图12所示。
由图12(a)可知,仿真前10 s 内ROV 由静止开始逐渐加速,直至推力τP、静力τR与流体动力τH相平衡时保持匀速斜航;图12(b)显示,此过程中纵倾角θ 亦稍增长后保持稳定,这是小攻角来流条件引起的孟克力矩[7]M =( )Xu˙- Zw˙uw 所造成的,体现出ROV 航行过程中纵向速度u 和垂向速度w 的耦合由于流体粘性力τD的大小与速度及速度二次项均相关,ROV加速过程中初始流体阻力τH远低于推力τP,经过一段时间加速后,流体阻力τH快速增长,ROV 接近受力平衡状态,速度u及纵倾角θ的变化速率趋缓,其非线性运动特性得以展现。
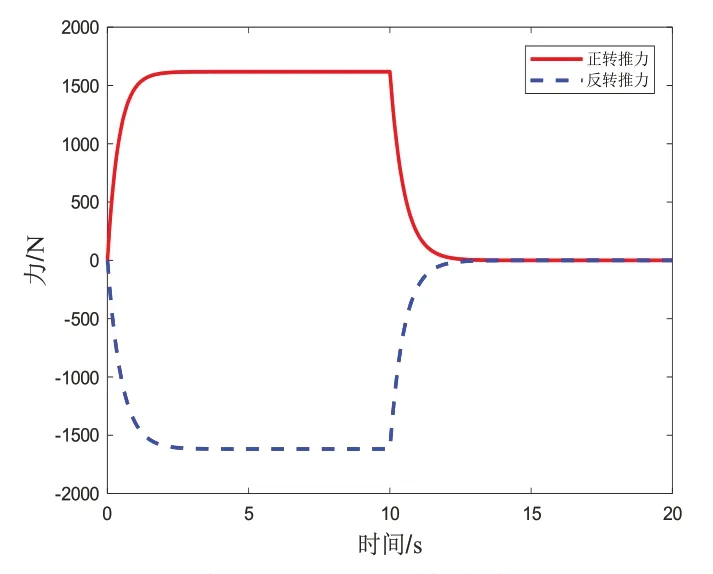
图10 推进器正、反转动态性能Fig.10 Dynamic performance of thruster in forward and reverse directions
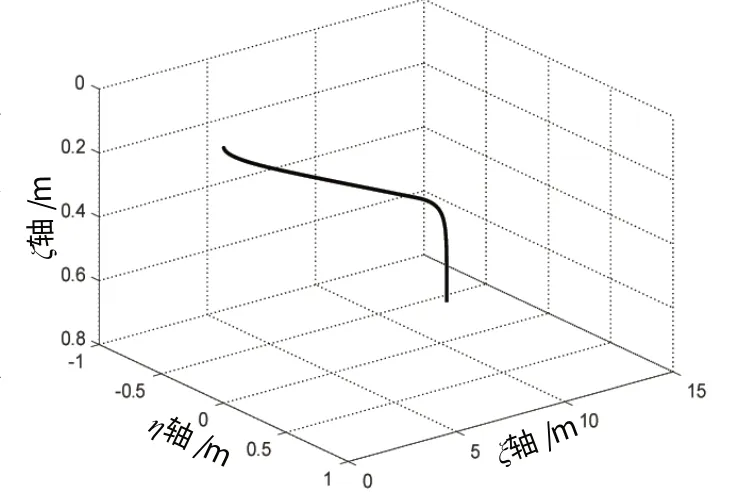
图11 ROV运动轨迹Fig.11 ROV trajectory
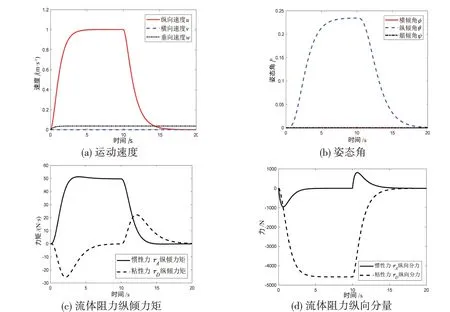
图12 ROV运动仿真结果Fig.12 ROV motion simulation results
仿真10 s后纵向推力τP逐渐归零,在刚体惯性与流体粘性力τD的作用下,ROV 纵向速度u不断减小至零,由于恢复力矩作用,纵倾角θ归零,ROV回归正浮、匀速下潜状态。
由图12(c)可知,流体惯性力τA对姿态角的影响更为显著,这是由于其科氏力矩阵CA中包含了不同自由度间惯性水动力系数与速度的耦合项;由图12(d)可知,粘性力τD纵向分量的数值较大,为影响ROV速度的主要因素,惯性力τA纵向分量仅在加速、减速初期产生较明显的非线性变化效应。
6 结 语
本文将Modelica语言应用到ROV力学系统的建模过程中,提出了一种通用的、面向对象的水下航行器建模方法,该语言如下特性与优势得以展现:
(1)陈述式特性更大限度地保留了力学系统理论拓扑结构,便于实现受力分析到仿真模型转化;
(2)层级划分机制使得图标视图与组件视图中的各级组件更为清晰,有利于模型的修改与测试;
(3)非因果特性在进行此类非线性、多耦合的复杂系统建模时优势明显,无需人工划分方程组数据流向,大大减少了建模工作量;
(4)继承与组件实例化机制提升模型重用性,通过定义可重用的动力学与运动学连接器并应用组件连接机制,模块间的互联得到保证。
将推进器动态性能仿真应用至ROV斜航下潜仿真工况内,仿真结果体现出ROV在实航过程中非线性及不同自由度间运动耦合的力学特性,该建模方法的合理性、便捷性得以展示。同时,该语言多领域建模特性保留了对ROV 真实物理系统实施进一步探究的可行性,为后续机、电、液、热、流等不同学科领域子系统接入提供了可能。

