桥梁转体施工坐标计算及线形监测方法研究

（中铁四局集团第四工程有限公司，安徽 合肥 230041）

0 前言

随着国家交通运输基础建设的不断发展，目前国家铁路网和公路网得到了不断的完善。从空间开发的角度思考，会有越来越多的新建公路、铁路工程与既有的公路或者铁路进行平面交叉施工或者跨越河道施工，而采用转体施工的方法可以达到减少对既有线路交通影响和降低安全风险的目的。

目前包含转体施工工序的在建工程在设计出图时，绝大部分设计只提供成桥后的中心轴线及坐标信息，并不包括转体前桥涵施工的坐标，而目前各个项目采用的方法大部分是绘制CAD图形后，将桥梁旋转至转体前位置，在CAD图形中直接提取坐标施工，这种方法存在无法提供计算过程、复核方法单一、容易造成偏差等诸多问题。

为了确保成桥后的线形符合设计要求，在转体施工过程中必须进行严格的施工监测。而现阶段监测的方法手段参差不齐，与所需成本不成比例。因此本文将从转体前坐标计算方法与转体过程中监测方法这两方面进行研究，以求证出一套科学合理且成本适中的方法。

1 研究思路

研究思路如图1。

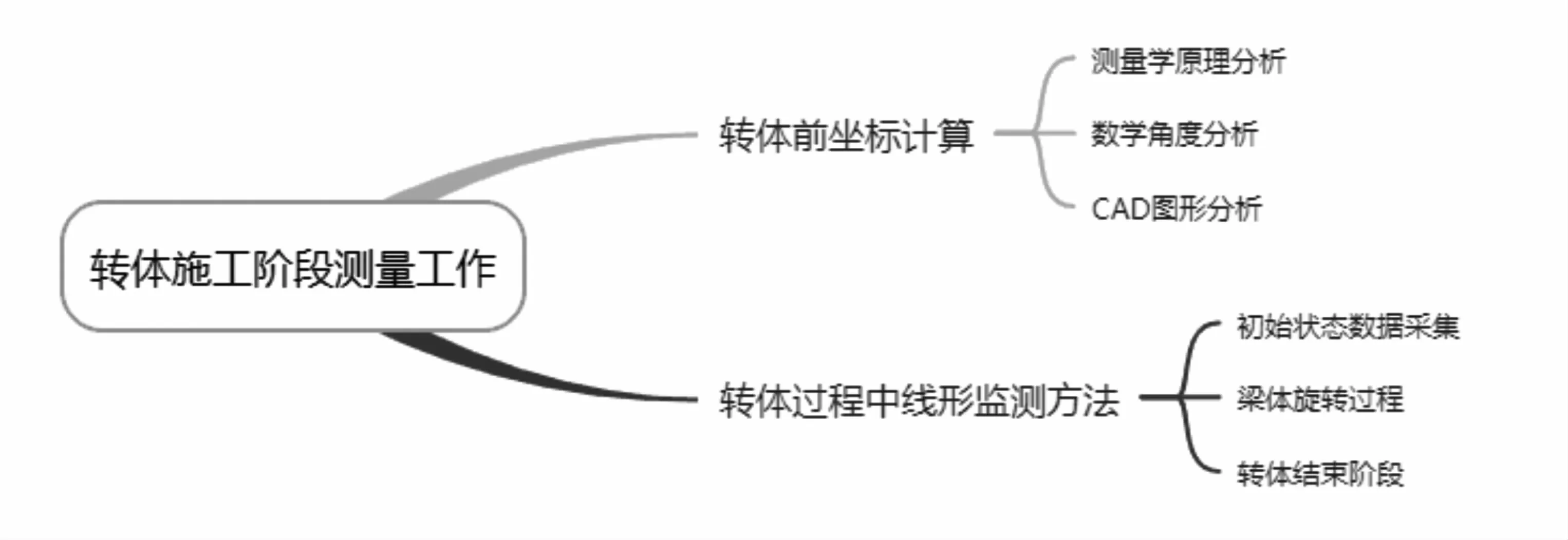
图1 研究思路图

2 转体前坐标计算

转体施工过程的一个关键控制点是保证桥梁转体完成后达到设计的线形要求，而坐标是反映线形的直接表现形式，因此坐标的计算是最为重要的一个基础条件。

成桥后的坐标计算可以根据设计给定的中心轴线信息，应用成熟的轴线计算软件或者线元法、交点法等方法计算得到。而桥梁转体前坐标计算则可从测量学、数学及CAD成图等方面由施工单位自行计算得到，并进行互相复核，以保证坐标计算的正确性。

2.1 方法一：测量学原理分析

根据转体施工过程的原理，可以发现，转体过程是以球铰为中心进行旋转的一个过程，旋转后使得桥梁线形符合设计要求，其过程如图2所示。

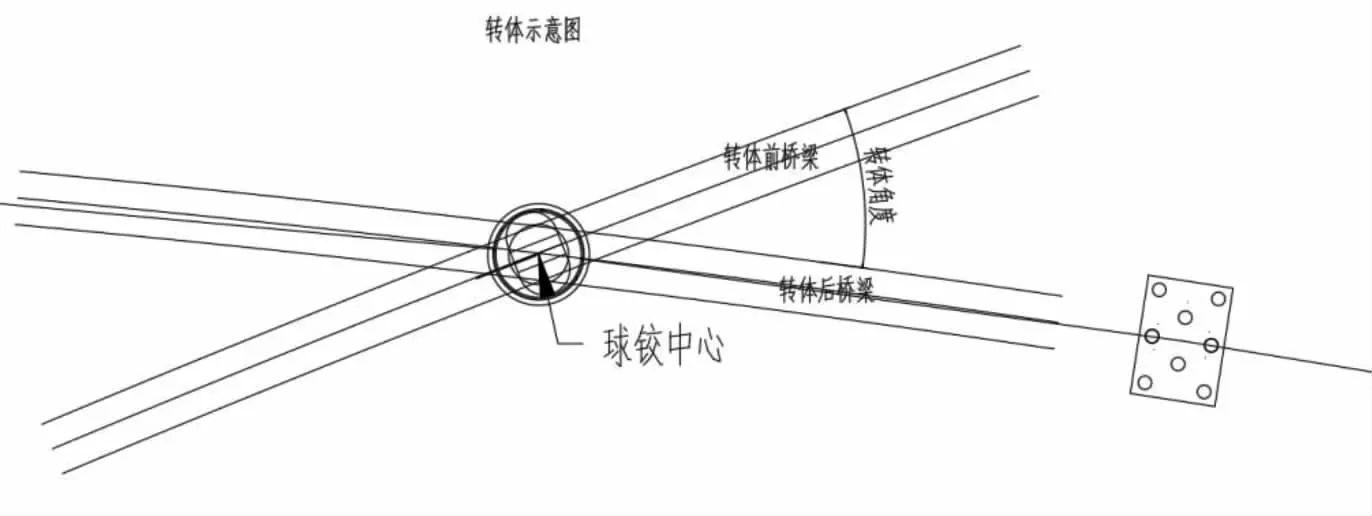
图2 桥梁平转示意图

桥梁转体前后，桥梁上各里程处的坐标值随着旋转角度的变化而变化，但是桥梁长度不变，球铰中心坐标保持不变，因此可以得出球铰中心到桥梁上各里程处的长度是保持不变的，如图3所示。

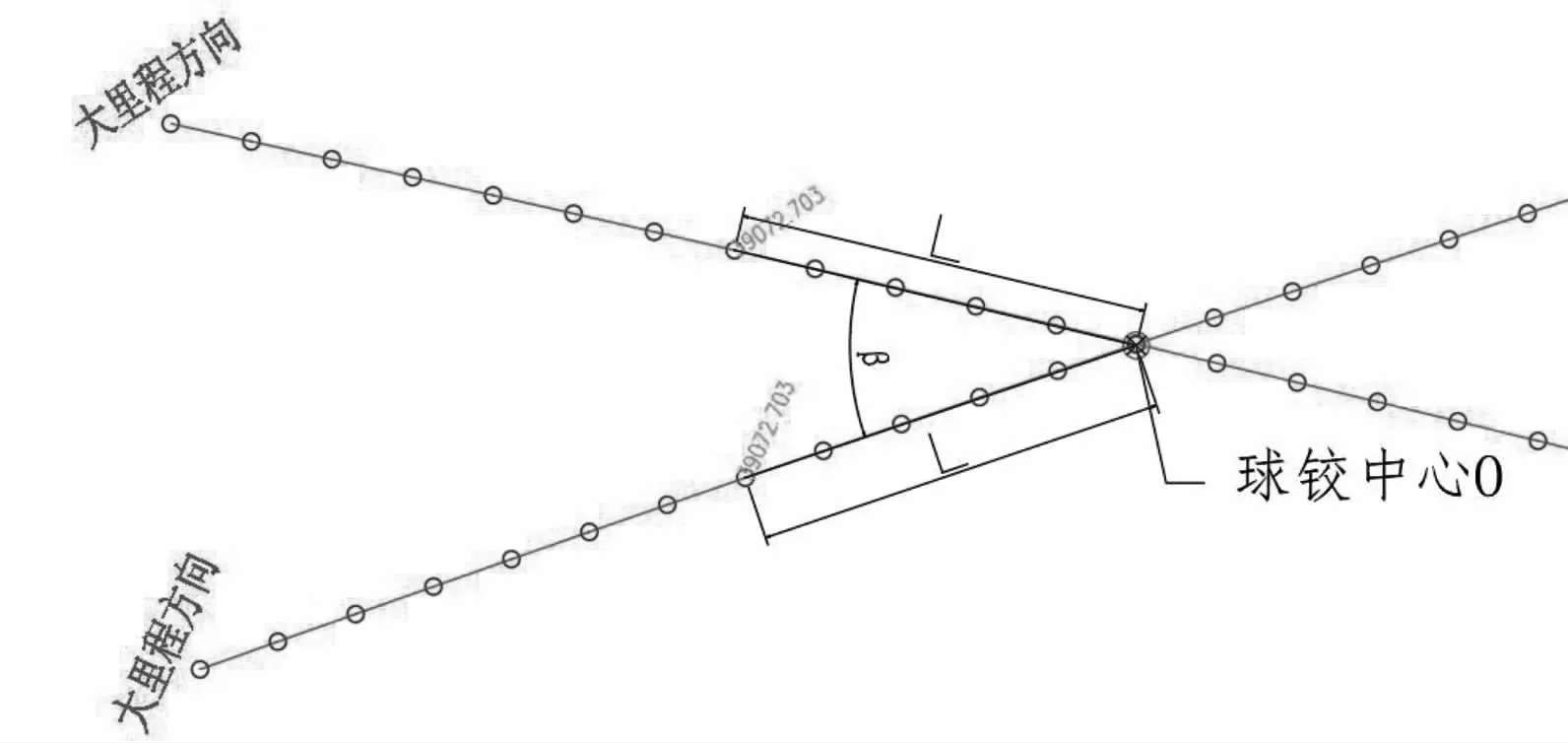
图3 桥梁平转简化图

成桥后桥梁上任一里程处坐标与球铰中心坐标可以计算得出，转体过程中任一里程处距球铰中心的距离L保持不变，并且形成的夹角β为桥梁转体角度。根据坐标正算与坐标反算的原理，即可求出转体前桥梁任一里程处的坐标。

如桥梁在成桥后某一里程点为A，球铰中心为 O，则 A 点坐标为（X，Y），O点坐标为（X，Y），桥梁转体角度为 β。求转体前该里程处A’的坐标。

根据坐标反算原理，可以计算出OA的距离L与方位角α。

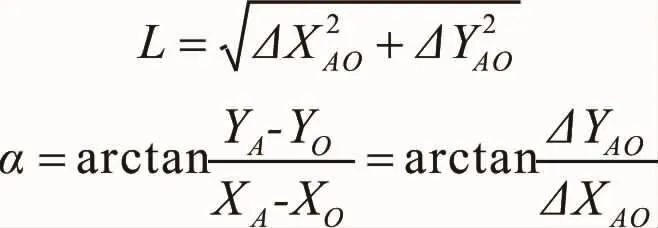
则球铰中心O点至转体前该里程处A’的方位角为α’，根据方位角顺时针增加，逆时针减小的原理可得：

α’=α-β

（若规定β值顺时针为正，逆时针为负，则公式可改写为：α’=α+β）

根据坐标正算原理，可以计算出转体前该里程处A’的坐标为：

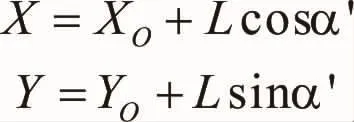
将此公式编制成EXCEL格式的文档，则可批量计算转体前所需的任一里程处中心坐标，进行指导桥梁施工。

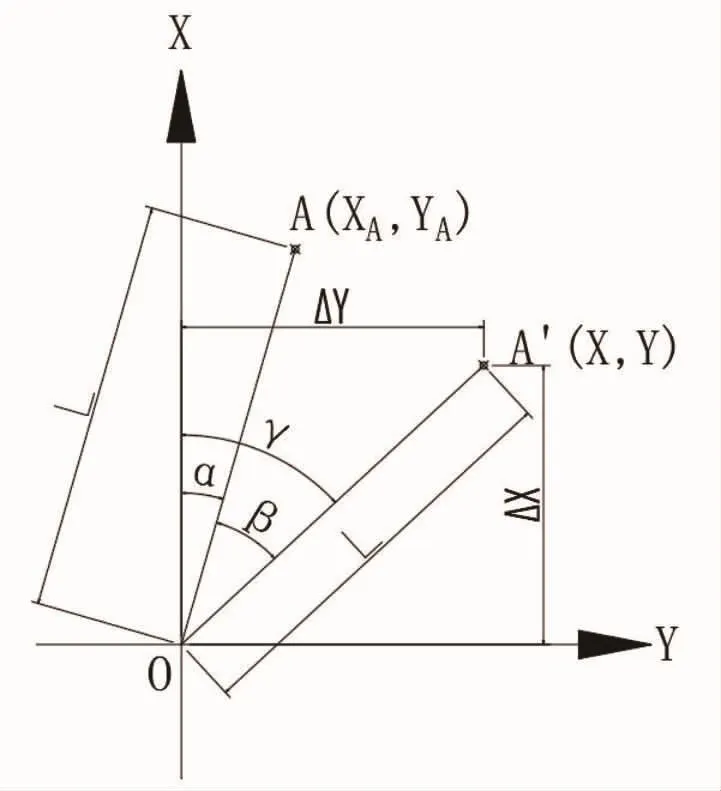
图4 数学角度分析

2.2 方法二：数学角度分析

转体前任一里程处A’的坐标与球铰中心O点的坐标有直接的联系，若将O点坐标假设为(0，0)，成桥后该里程点A坐标为（X，Y），则可将转体模型在坐标系中的关系更加简化，如图4。

夹角β为桥梁转体角度。

则根据图形可得：

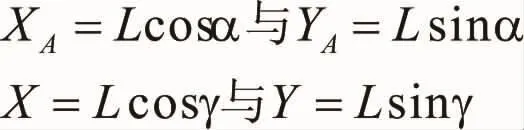
根据γ=α+β与三角函数的运算法则，将上述公式合并后可得：

综上所述，若规定β值顺时针为正，逆时针为负，则成桥后任一里程处A点（X，Y）在绕球铰中心 0 点（X，Y）转体前的坐标为：

同样将此公式编制成EXCEL格式的文档，可批量计算转体前所需的任一里程处中心坐标，进行指导桥梁转体前施工。

2.3 方法三：CAD图形分析

经过测量学与数学角度的分析后，我们可以在CAD软件中直接将设计给定的成桥后中心轴线画出，并根据转体角度将其绕球铰中心进行旋转，然后得到转体前的中心轴线，使用坐标提取工具得到转体前任一里程处的坐标，如图5所示。

图5 CAD图形分析

在CAD软件中可以使用标注角度、标注距离等多种方法进行转体前图形的复核。

2.4 计算方法比对分析

使用三种计算方式统一计算某一项目转体前桥梁中线坐标后，三种计算方式所得结果对见表1。

三种方式的计算结果对比均小于1mm，但由于CAD提取坐标时由于精度与坐标值取位问题，导致与其他两种计算方式有1mm内的偏差。

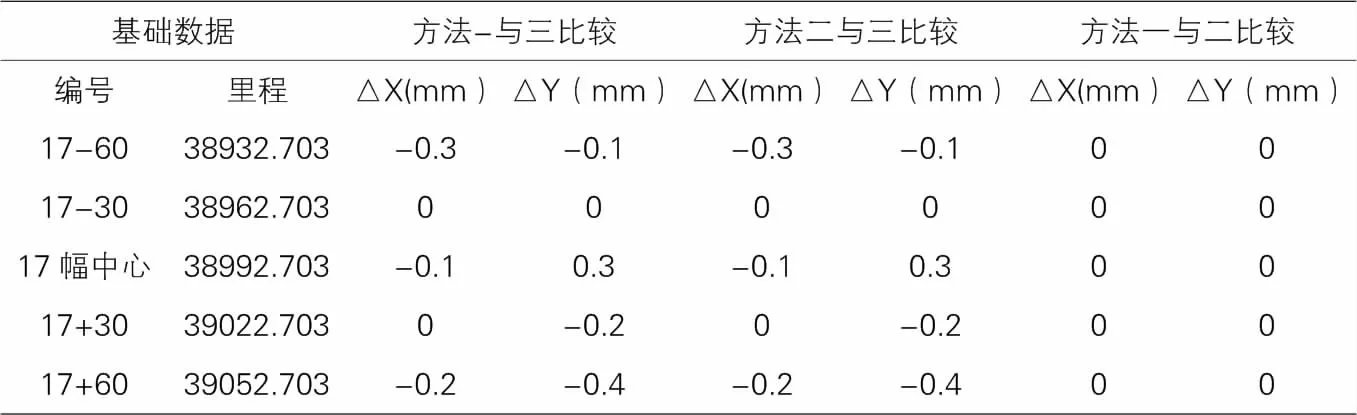
成果分析表 表1

方法对比表 表2

将三种计算方式的优缺点总结归纳见表2。

在桥梁转体项目中应用时，可以根据本项目不同阶段的需求来选择适合的方法进行坐标计算并互相校核。

3 转体过程中线形监测方法

在保证了转体前梁体坐标的准确性后，另一个保证桥梁转体完成后达到设计的线形要求的关键控制点为桥梁合拢精度。并且为减少施工对铁路运营的干扰，安全跨越铁路干线，确保大桥的工程质量和施工安全，保证施工进度，必须进行全过程监测和监控，根据监测的实际情况指导和配合现场施工。

3.1 初始状态数据采集

转体过程中梁端的平衡稳定是转体成功的关键。因此除了监测梁体轴线的变化，还需要在梁端预埋观测棱镜，以方便转体工程中进行及时的观测，以指导转体施工。

图6 梁端预埋观测棱镜位置示意图

在转体前期对预埋棱镜进行多频次的初始值采集，在确定轴线稳定的基础上，将初始数据进行对比分析后，使用差值稳定的数据求平均值，作为最终转体施工的初始值。

3.2 梁体旋转过程

转体过程是一个动态的过程，其线形控制点的空间坐标是不断变化的，且变化幅度很大。因此，过程中对桥梁状态理论坐标计算为转体过程中监测的关键。

转体过程中，采用全站仪对棱镜位置进行观测，实时对梁体轴线进行动态观测，以便随时掌握结构变形影响，根据观测数据及时调整转体速度，正确指导施工，确保转体精确就位。

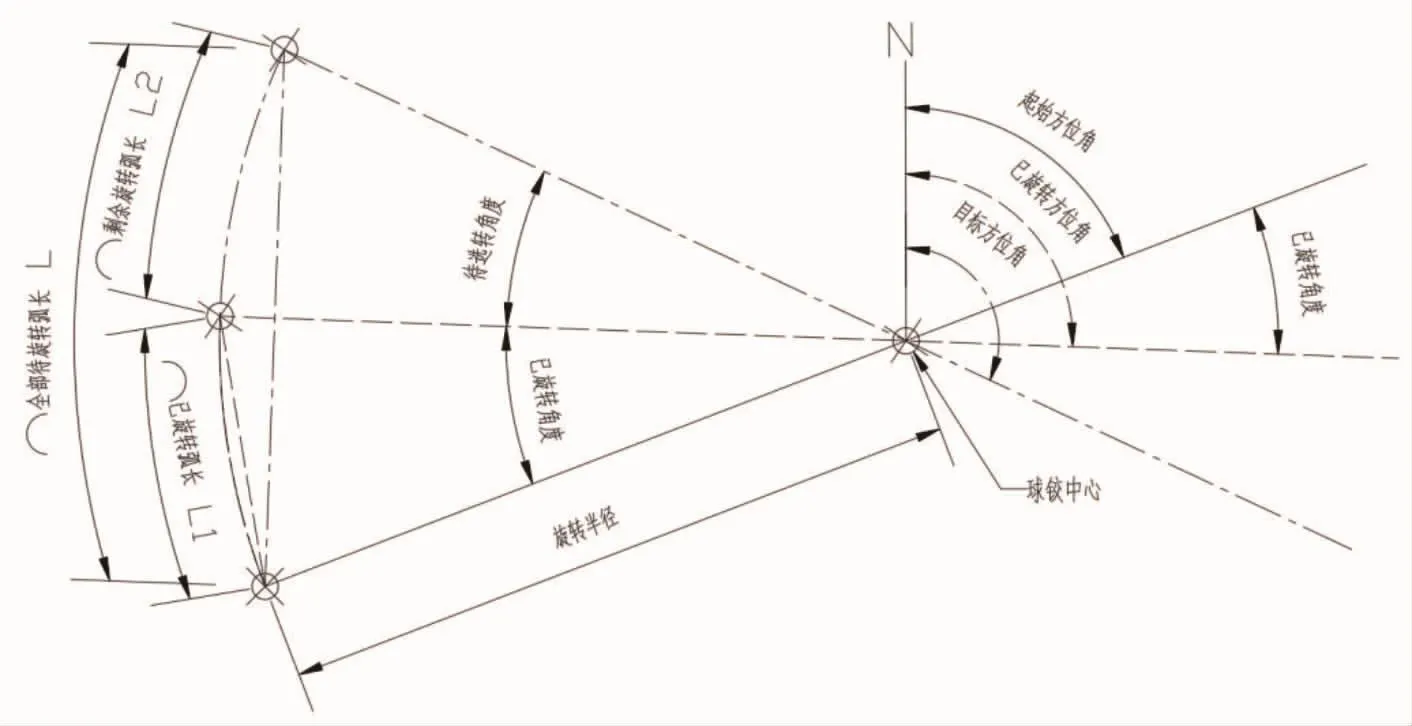
图7 梁体旋转过程观测因素示意图

根据坐标反算原理计算出旋转半径r与方位角α：

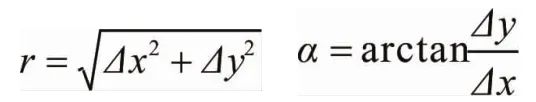
通过图示关系即可求出已旋转角度与待旋转角度；根据弧长计算公式L=α×r可计算出已旋转弧长与剩余旋转弧长。

将计算公式整理后汇总成EXCEL表格，在转体过程中根据观测固定在梁端轴线位置的棱镜，进行动态追踪水平转动情况，即时计算转动角度、转动弧度等数据。

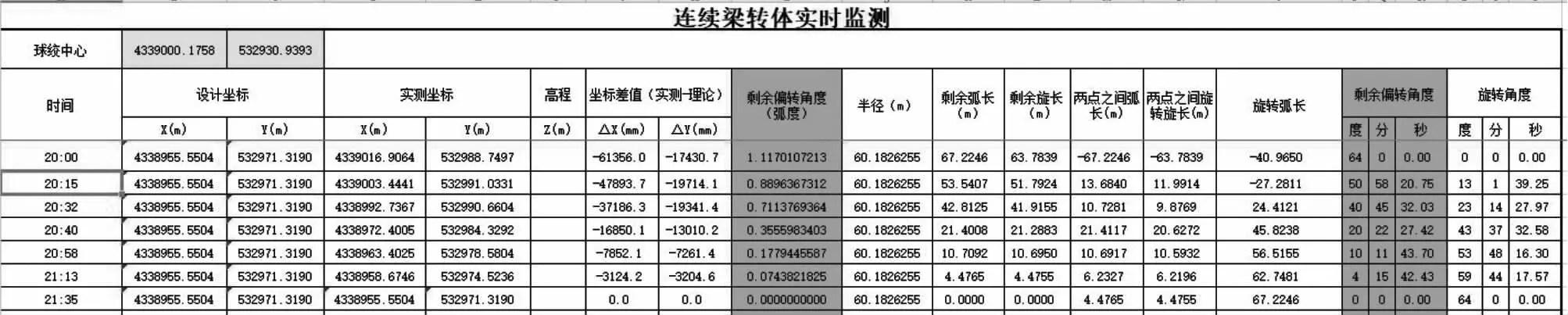
图8 观测记录表示意图

3.3 转体结束阶段

桥梁转体到位后，在主梁进行姿态调整，对进行高程测量。平转到位及箱梁合龙前，对所有测点进行连续两天全天候测试，转动体系完成后静置期间，悬臂前端高程变化监测每3 h测1次，连续观测1昼夜。采用精密水准测量仪器进行观测。

4 结语

经过合安铁路上行联络线跨合武绕行铁路连续梁、商合杭铁路上跨合宁铁路特大桥及荣乌高速上跨京霸铁路特大桥等多个转体项目的实际应用，不仅保证了转体施工的精确合龙，也充分证实了本套理论的可靠性、准确性与可实施性。