二维黑磷的光学性质*

黄申洋 张国伟 汪凡洁 雷雨晨 晏湖根†

1) (复旦大学物理学系, 上海 200438)

2) (西北工业大学柔性电子研究院, 西安 710129)

1 引 言

2004 年石墨烯的问世[1]标志通往二维材料世界的大门被打开.经过科学家们的不断探索, 至今已有几百种二维材料相继被发现[2-4], 材料的种类包含了二维半金属、二维半导体、二维绝缘体, 二维铁磁材料等.二维材料中蕴含了丰富有趣的物理现象, 如半整数量子霍尔效应[5,6]、Klein 隧穿等[7];另外二维材料表面原子级平整且不受晶格匹配的限制, 不同的二维材料之间可以如同堆积木方式相互堆叠形成范德瓦耳斯异质结[8], 从而进一步丰富了二维材料的物理特性, 如: 在魔角石墨烯中的反常超导[9], 石墨烯-氮化硼莫尔超晶格中的霍夫斯塔特蝴蝶(Hofstadter’s butterfly)及分数量子霍尔效应[10], 超长寿命的层间激子[11]和莫尔激子[12],可调控的莫特绝缘体[13-15]等, 使得二维材料具有极其广泛的研究与应用价值.

二维黑磷是2014 年才加入二维材料的大家族, 最早是由复旦大学Li 等[16]进行了研究报道,他们展示了基于少层黑磷制成的场效应晶体管(FET)不仅具有高达105的开关比, 同时室温下具有不俗的载流子迁移率(约1000 cm2/V).随后二维黑磷以其优异的性质很快引起了人们广泛研究兴趣, 在2014—2015 年一年间就有近百篇关于黑磷的研究论文发表[17].不同于石墨烯、过渡金属硫族化合物(TMDCs)等其他的二维材料, 黑磷具有以下特性.1)黑磷具有面内褶皱的原子结构(如图1),具有很强的面内各向异性; 通常把沿着x 方向称为扶手椅方向(AC), 把沿着y 方向称为Z 字形方向(ZZ); 这种独特面内晶体结构也导致了黑磷各向异性物理特性[18-21], 这不仅提供了各向异性材料物理特性的研究平台, 同时可为器件设计提供新的自由度.2)黑磷从二维的单层、少层到三维的块材都为直接带隙半导体, 并且黑磷的带隙随厚度变化十分显著, 带隙可从单层的1.7 eV 随着厚度的增加逐渐缩减至块材的0.3 eV[22,23], 覆盖了中红外到可见光波段, 这恰好填补了零带隙的石墨烯和带隙在可见光的TMDCs 间的空白, 带隙变化范围之广也是其他的二维材料所不能比拟的.当前有关黑磷的研究已经取得了相当多的研究成果, 本文则主要介绍有关黑磷光学性质方面的研究.主要包括二维黑磷本征的光学性质和调控两部分, 其中在本征的光学性质部分将会对黑磷的带间跃迁吸收、激子效应、光致发光、光学性质的稳定性等研究展开介绍,而在光学性质的调控部分主要对应变调控、栅压调控等研究展开介绍, 并在最后做了总结与展望.

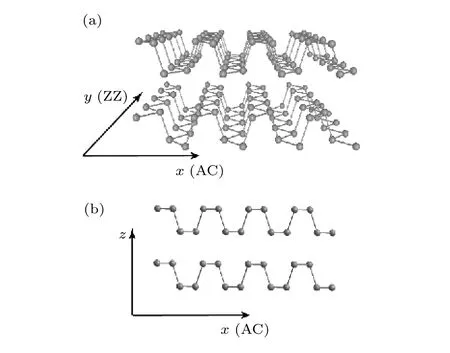
图1 黑磷的原子结构 (a)两层黑磷的原子结构的立体图; (b)侧视图Fig.1.Atomic structure of BP: (a) Structure of bilayer BP;(b) the side view.

2 二维黑磷的本征光学性质

2.1 二维黑磷的带间跃迁吸收

带间跃迁吸收是半导体材料最基本的光学性质之一, 通过对带间跃迁吸收的研究可以获得带隙、光电导等重要的信息.Li 等[24]对1—5 层黑磷的带间跃迁吸收做了研究报道, 他们对77 K 下蓝宝石衬底上黑磷进行了近红外、可见光波段反射谱表征(ΔR/R), 如图2(a)—(c)所示, 其中黑色、红色线条分别代表了入射光偏振沿着AC, ZZ 方向时的反射谱.当测试样品在透明衬底上且样品的厚度远小于入射光波长时, ΔR/R 正比于吸收强度[25,26],由此便可得到吸收信息.可以看到单层的光学带隙吸收在1.73 eV, 并且只有入射光偏振沿着AC 时才可以被观测到, 说明黑磷带间跃迁吸收具有明显各向异性.这源自黑磷独特的褶皱面内原子结构,具体来说黑磷面内原子结构关于x-z 平面具有镜面对称(见图1), 同时理论计算表明二维黑磷的价带顶和导带底且主要由s, px, pz轨道构成并且关于x-z 镜面具有偶宇称[22,27], 因此当入射光沿着ZZ(y 轴)时存在关于x-z 镜面的奇宇称使得跃迁矩阵元为0, 跃迁被禁止.另外值得注意的是, 两层黑磷的光学带隙红移至1.15 eV, 同时在2.44 eV 出现了新的吸收峰, 而3 层带隙为0.83 eV, 新的峰则红移到1.97 eV.几乎在同一时间, Zhang 等[28]采用傅里叶变换红外光谱(FTIR)技术对室温下石英衬底上的2—15 层红外波段吸收的进行了研究(如图2(d)—(f)), 得到了同样的实验现象.事实上这些新的吸收峰是少层黑磷中的层间相互作用的产物[27]: 对于N 层黑磷, 层间相互作用使得倒空间Γ 点处成N 对分离的导带(c1, c2, ···, cn)和价带(v1, v2, ···, vn), 新的吸收峰则是更高阶数的价带到导带间的跃迁, 如v2—c2, v3—c3等跃迁(如图2(h)), 另外如同量子阱中的选择定则要求, 只会有导带和价带指数相同的即Δn = 0 跃迁.关于带间跃迁吸收峰位的层数依赖, 可以通过一维紧束缚模型得到吸收峰位关于层数N 以及跃迁阶数n 的解析表达式:

其中, Eg0为单层的带隙, γc(γv) 为导带(价带)最近邻层间相互作用.虽然该模型没有考虑激子效应, 但仍然可以较好的描述带间跃迁吸收的层数及跃迁阶数的依赖关系(如图2(g)).

少层黑磷带间跃迁吸收的峰位具有明显层数依赖关系, 但是有意思的是Zhang 等[29]最近研究发现带隙附近连续的带间跃迁吸收(图3(a)中箭头所指部分)却为一个常数, 并通过 k ·p 模型进一步得出吸收 A (ℏω) 可以表达为

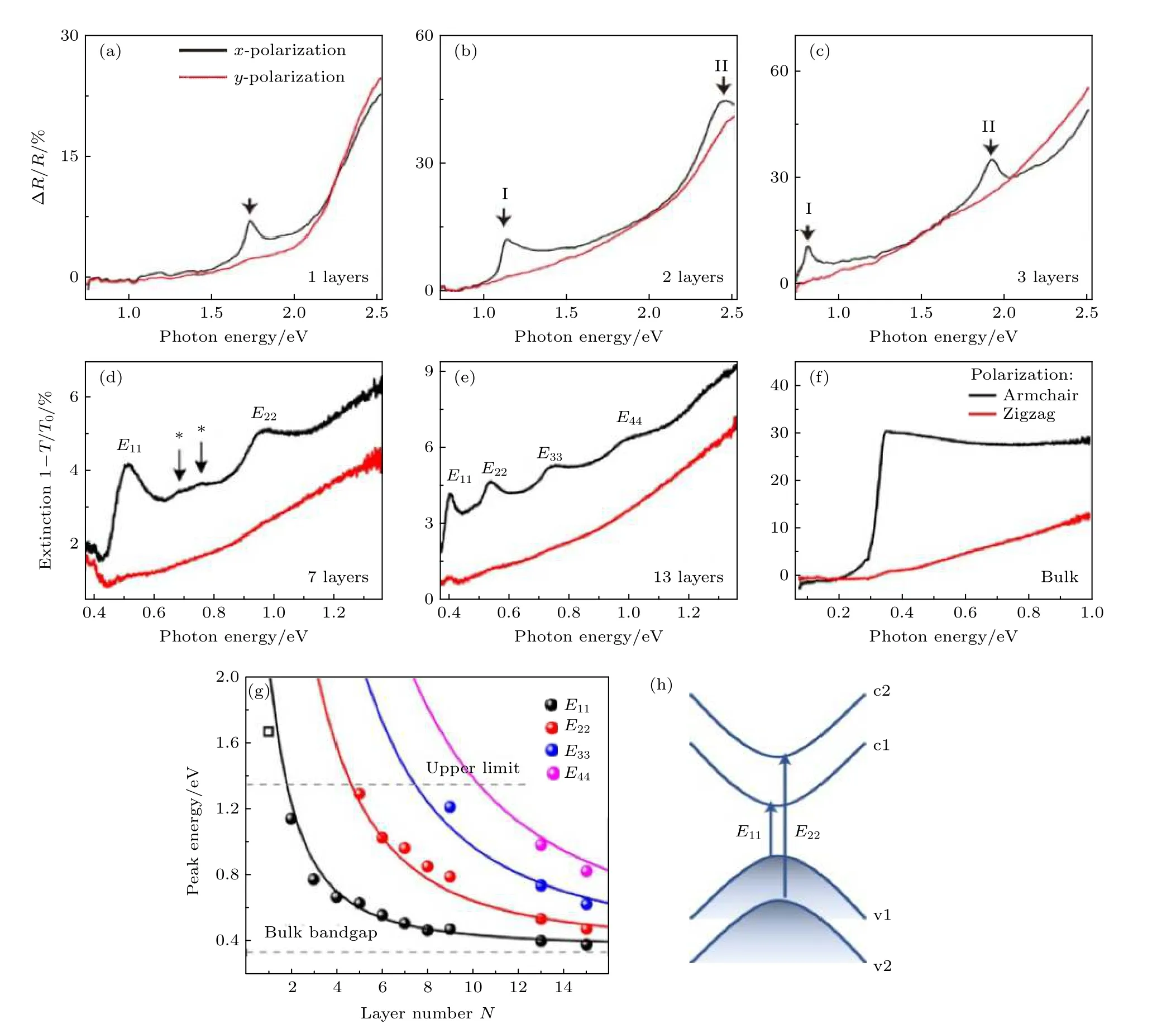
图2 二维黑磷的带间跃迁吸收 (a)-(c) 1-3 层黑磷的反射谱(ΔR/R)[24]; (d)-(f) 7 层、13 层和块材黑磷的红外消光谱(1—T/T0)[28]; (g) 带间跃迁吸收峰随层数依赖关系[28]; (h) 不同量子数子带间的跃迁示意图Fig.2.Interband transition absorption of 2D BP: (a)-(c) Reflection spectra(ΔR/R)[24] of 1-3 layers BP; (d)-(f) infrared extinction spectra of 4 layers, 7 layers, 13 layers, and bulk BP[28]; (g) interband transition energy as the function of layer number[28]; (h) schematic illustration of the optical transitions between quantized subband.

其中, gs,gv分别为自旋、能谷简并度, α 为精细结构常数(约1/137), Eg为带隙, µx, µy分别为沿着AC方向和ZZ 方向的电子-空穴约化质量,θ(ℏω −Eg)为阶跃函数.由此可知在带隙附近的吸收只取决于µy, µx间的比值, 对从第2 个价带到第2 个导带(E22)的吸收也是如此(如图3(b)所示).其实这种连续的带间跃迁吸收强度为常数的现象普遍存在于二维材料中, 比如单层石墨烯中从红外到可见波段吸收都为2.3%[25,30].可以由费米黄金法则(Fermigolden rule)知连续的带间吸收大小主要取决于两部分, 即跃迁矩阵元和态密度, 并且二者都依赖于能带结构, 而当二者有关能带结构的表达项相抵消时, 则会出现吸收强度的为常数的情况.然而黑磷与石墨烯等其他二维材料[25,30]截然不同的是, 单层和少层黑磷的连续带间跃迁吸收都是相同的, 即没有层数依赖(见(2)式), 而对于石墨烯而言, 两层吸收是单层的2 倍, 这主要是因为黑磷带间跃迁发生在倒空间Γ 点, 各个子带是非简并, 不论单层还是少层黑磷, 始终只有一对价带、导带参与带间跃迁吸收, 同时 µy, µx基本保持不变, 所以即使层数增加吸收强度也不变; 而石墨烯等带间跃迁发生在K 点, 各子带为简并的, 层数越厚参与跃迁的子带数目越多从而带间吸收越强.

图3 少层黑磷带隙附近连续的带间跃迁吸收 (a)聚二甲基硅氧烷(PDMS)衬底上6 层黑磷的光电导[29]; (b) 不同子带间的带间跃迁带隙处连续吸收部分的吸收强度(图(a)中箭头所示)随层数的变化[29]Fig.3.The absorption of continuum part near bandgap in few-layer BP: (a) Optical conductivity of 6 layers BP on PDMS substrate[29]; (b) the continuum height of each subband transition near the corresponding band edge (as indicated by arrows in fig.3(a))is plotted as a function of layer number[29].

2.2 二维黑磷中的激子

通常在半导体材料中, 电子和空穴由库仑作用束缚在一起形成新的准粒子—激子.激子与氢原子非常类似, 都是由正负电荷构成, 吸收谱为洛伦兹谱形.类比于氢原子可以将激子的能态按量子数依次命名为1s 态、2s 态、2p 态等.其中1s 态为基态也称光学带隙, 而能带结构的带隙与光学带隙的差值称为激子束缚能.对于三维半导体, 激子束缚能通常只有十几个meV, 因此室温下激子效应几乎可以忽略.而在二维材料中, 由于介电屏蔽作用的减弱及量子受限效应, 激子束缚能可高达几十到上百个meV[31,32], 此时激子效应便对材料的光学性质起到了不容忽视的作用.早在2014 年Tran等[33]就对单层黑磷的激子束缚能做了计算, 结果表明单层黑磷的激子束缚能高达900 meV, 他们将如此大的激子束缚能归于黑磷各向异性能带结构.紧接着在2015 年Wang 等[34]对单层黑磷进行了光致发光激发光谱(PLE)实验, 同样得到单层黑磷即便在氧化硅/硅衬底上激子束缚能也有近900 meV.但之后却有理论计算表明[35], 悬浮的单层黑磷激子束缚能只有480 meV, 这几乎是之前结果的一半, 而被包裹的单层黑磷激子束缚能只有140 meV, 因此关于单层黑磷激子束缚能的大小仍然存有争议.随后Zhang 等[36]利用FTIR 对2—8 层黑磷的激子束缚能做了详细的研究: 得益于极高的样品质量, 光学带隙处可测到一个非常尖锐(半高宽约为20 meV)吸收峰, 这便是1s 态激子的吸收(如图4(a)), 此外在高于1s 态吸收峰位存在一个吸收较弱且较宽的吸收峰是激子2s 态的吸收, 2s 态吸收在2—6 层中都可以被清楚观测到,而在7 层及更厚的样品中则难以被分辨.在二维氢原子模型中, 由1s 态和2s 态的能量差Δ12可确定束缚能Eb, 即Eb= 9/8Δ12, 然而对于二维材料中的激子情况则不同, 这是因为二维材料中库伦屏蔽作用是空间非局域化的[31], 为此Zhang 等[37]借助Keldysh 模型进一步计算了2—6 层黑磷激子的1s, 2s 能级位置和带隙Eg, 其中计算得到1s,2s 的能级位置与实验观测值相一致从而确保了计算结果的可靠性.如图4(b)所示, 黑磷激子束缚能Eb为Δ12的两倍, 从2 到6 层依次为213, 167,139, 120, 106 meV, 在聚二甲基硅氧烷(PDMS)衬底上单层黑磷的则为316 meV.显然黑磷激子束缚能Eb具有明显的层数依赖关系, 为此Zhang等[38]在已有的模型基础上提出了层数依赖的有效层极化率的概念, 从而得到黑磷激子束缚能Eb关于层数N 的解析表达式为:

其中, α0, α1分别为衬底和单层黑磷的极化率.如图4(c)所示, 该模型可以很好的对不同层数激子束缚能进行拟合.由于该模型只含有描述介电屏蔽作用的物理参量—极化率, 并没有考虑量子限制效应, 因而可以认为厚度对激子束缚能的影响主要是由介电屏蔽作用的改变而引起的.

图4 层数依赖的激子 (a) PDMS 衬底上4 层黑磷的消光谱[36]; (b) 1s, 2s 能级以及电子结构带隙的层数依赖[36]; (c) 激子束缚能的层数依赖关系[36]; (d) 激子吸收峰的积分面积随层数的变化, 散点为实验数据点, 黑色曲线为1/N 曲线, 红色曲线为1/(χ0+Nχ1)拟合曲线[29]Fig.4.Layer dependent exciton: (a) The extinction spectrum of 4 layers BP on PDMS substrate[36]; (b) layer dependence of 1s, 2s transition energies and quasi-particle bandgap[36]; (c) scaling behavior of exciton binding energy with layer number[36]; (d) the frequency-integrated conductivity of the 1 s exciton as a function of layer number.Dots are experimental data, which fitted by the red curve using the relation 1 /(χ0+Nχ1) , and the black dashed curve shows the 1/N relation[29].

随后Zhang 等[29]对少层黑磷激子吸收强度做了研究.令人惊讶的是, 黑磷层数越薄激子吸收反而越强, 正如图4(d)所示.对此比较直观的理解为: 激子的吸收强度正比于 Lz·|φex(0)|2, 其中 Lz为样品的厚度,|φex(0)|2为在电子和空穴出现在同一位置的概率[39,40], 更薄的层数具有更强的量子限制效应, 从而将导致更大的|φex(0)|2, 对于量子阱有和厚度 Lz(N) 成反比的关系, 即层数越薄吸收反而越强.然而实际上激子吸收强度随厚度的变化不完全遵循1/N 的关系(如图4(d)中虚线所示).为了能够更准确地描述激子吸收强度的层数依赖关系,Zhang 等提出了进一步的解释, 他们认为激子的吸收强度与激子束缚能成正比, 这是符合预期的, 因为更大的激子束缚能意味着电子与空穴离得更近从而更有利于吸收光形成激子态.根据之前的结论可知激子的束缚能和有效极化率(χ0+Nχ1)成反比,从而激子吸收强度也反比于(χ0+Nχ1)(如图4(d)中红线所示).值得注意的是, 对于悬浮的黑磷(即不考虑 χ0)激子吸收的强度仍然遵循1/N 的关系.[41], 从而可以得到激子的吸收强度

2.3 二维黑磷的光致发光

光致发光(PL)为吸收的逆过程, 为半导体材料的另一个重要光学性质.黑磷从单层到块材都为直接带隙半导体, 因此具有较高的发光效率, 这非常利于在发光器件如激光器、发光二极管中(LED)的应用.当前已经有不少关于二维黑磷PL 的研究报道[24,34,42,43].然而在不同研究报道中PL 峰位有不小的差异, 这源自黑磷样品质量的差异.值得注意的是PL 对样品的质量是非常敏感的, 因此PL并不是一种好的手段来研究带隙, 相比之下从吸收谱得到带隙信息更本征.Likai Li 等[24]对77 K 下1—3 层黑磷的PL 做了测试并与吸收做了对比(如图5(a)—(c)所示), 其中在黑磷共振吸收的位置可以观测到非常强的PL 信号, 这正是直接带隙的特征.由于PL 过程为吸收的逆过程, 因此黑磷的PL也是具有明显的各向异性, 其发光具有线偏振的特性且偏振沿着AC 方向.值得注意的是这里PL峰位要略低于吸收峰的, 通常将二者的差值称为斯托克斯位移, 造成斯托克斯位移主要是位于禁带中的缺陷态发光造成.最近Chen 等[43]利用FTIR 对4.5 nm(9 层)—46 nm 厚的黑磷做了PL 探测, 发现黑磷在0.308 eV (46 nm)至0.441 eV (4.5 nm)的中红外波段同样具有非常强的PL (图5(d)), 并且PL 峰位的厚度依赖关系与之前吸收光谱中的相吻合(图5(e)), 从而进一步验证了黑磷从单层到块材都为直接半导体.

图5 二维黑磷的光致发光 (a)-(c) 77 K 下单层黑磷的光致发光及反射谱, 其中黑线为探测方向沿着AC 的发光谱, 红线为探测方向沿着ZZ 的发光谱, 蓝色虚线为反射谱[24]; (d)80 K 下4.6 nm (约9 层)到46 nm(约92 层)的黑磷发光谱[43]; (e) 发光峰位随着层厚的变化关系[43]Fig.5.Photoluminescence (PL) of 2D BP: (a)-(c) The PL and reflection spectra of 1 layer BP under 77 K, black curve is the PL detected alone AC, the red is PL detected alone ZZ and blue dashed curve is the reflection spectrum[24]; (d) PL of BP with thickness ranging from 4.6 nm (about 9 layers) to 46 nm (about 92 layers) under 80 K[43]; (e) layer dependence of PL peak position[43].

2.4 二维黑磷光学性质的稳定性

虽然黑磷本身具有许多优异的性质, 但二维黑磷在空气中是非常不稳定的[44-46], 这非常不利于黑磷在实际中的应用.黑磷具有5 个价电子, 其中只有3 个配对形成共价键留下2 个未配对的价电子, 这导致了黑磷非常容易被氧化形成氧化磷(PxOy),而氧化磷又易溶于水从而进一步破坏黑磷的结构,从而影响黑磷的电学、光学等性质.其中Wang 等[47]对少层黑磷的光学性质稳定性进行了研究报道.如图6(a)所示, 对于3 层黑磷即使在空气中只有5 min, 吸收峰出现明显的蓝移并伴随着强度的减弱及峰宽的增加, 同时研究还发现层数越薄的黑磷,吸收峰位对空气越敏感(如图6(b)), 而这些吸收峰位的移动源自黑磷能带结构的变化, 对此Wang等借助量子阱模型做出了解释: 可以将本征的黑磷视为无限深方量子阱, 以导带变化的情况为例, 由于表面被氧化形成氧化层从而在阱底引入了附加势垒Δ (见图6(b)中的插图), 这会导致黑磷量子阱有效宽度减小从而能级出现蓝移, 相应的吸收峰蓝移, 进一步数值计算表明阱宽越窄量子阱的能级对附加势垒高度越敏感.随着时间增加, 等效的氧化层厚度不断增加直至表面1 层黑磷完全被氧化,此时3 层的黑磷减薄为2 层, 相应的吸收也蓝移至了2 层的峰位.另外Wang 等对暴露在空气中黑磷的PL 做了测试, 发现PL 峰同样随着暴露时间增加出现蓝移, 同时发光效率显著减弱并且伴随着斯托克斯位移增加, 这是由氧化引入更多的缺陷态所导致(如图6(c)), 由此可见相较于PL, 吸收谱能得到更本征的带隙大小.

图6 暴漏在空气中黑磷的光学性质[47] (a) 暴露在空气中3 层黑磷消光谱的变化; (b) 3 层和8 层黑磷的光学带隙(E11)在空气中的变化图; 插图为空气中黑磷导带结构变化的示意图, Δ 为黑磷氧化后引入的附加势垒; (c)暴露在空气中的3 层吸收峰以及PL 峰位的变化Fig.6.Optical properties of air-exposed BP[47]: (a) Evolution of extinction spectrum of an air-exposed 3 layers BP; (b) evolution of E11 peak energies of the air-exposed 3 layers and 8 layers samples, and the inset fig is the schematic illustration of evolution of conduction band in air-exposed BP; Δ is a barrier introduced by oxide; (c) blue shifts of absorption and PL peaks in an air-exposed 3 layers BP.

3 二维黑磷光学性质的调控

3.1 应变调控

应变可以通过改变原子间的键长来对材料的能带结构产生影响, 进而改变材料的光学性质.相较于三维材料, 在二维材料中施加应变的方式更简单有效, 因此应变调控也被广泛应用于二维材料的研究中[48-50].而相较于石墨烯、TMDCs, 黑磷具有更小的杨氏模量因而更容易被应变调控[51].早期Quereda 等[52]通过褶皱黑磷方式对10 nm(约18 层)的黑磷施加了应变, 其中在褶皱峰(谷)处黑磷会受到张(压)应变, 他们发现黑磷在可见光波段的吸收边在压应变(张应变)下出现了明显的红移(蓝移), 虽然该吸收边并不能真正反映带隙的变化(10 nm 黑磷带隙在中红外波段), 但仍具有一定启发性, 暗示了黑磷带隙对应变调控非常敏感.随后Zhang 等[28]利用FTIR 仔细地研究了单轴应变对二维黑磷能带的调控, 他们采用两点法的方式实现了最大0.92%的应变, 研究结果显示在张(压)应变下黑磷的E11, E22等吸收峰位都出现蓝(红)移,并且0.92%张应变可以将光学带隙(E11)从0.54 eV调控至0.65 eV, 相对变化23%, 由此可见单轴应变可以非常有效的对黑磷的带隙进行调控(图7(a)—(c)).值得注意的是, 虽然黑磷具有各向异性的结构, 但是如图7(c)所示沿着AC 和ZZ 方向的应变对能带的调控没有展现出明显的差异, 相同的现象在Zhang 等[53]研究中也被观测到.对此Zhang 等认为这是由黑磷面内各向异性的泊松效应所导致的: 对于单层黑磷由紧束缚模型可知其带隙随应变变化可表达为[54,55]

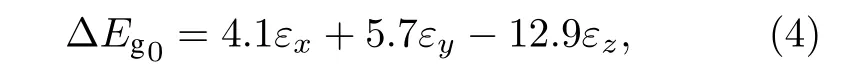
其中, εx, εy, εz分别为沿着AC, ZZ 和垂直于材料平面(z 轴)方向的应变.可以看到对于只有单个方向的应变存在时, 带隙在应变沿着ZZ 方向时会变化更快.然而实际中需要考虑泊松效应[56], 即面内的应变同样会引起垂直于面方向的应变, 在沿着AC(x)方向张应变(εx＞0)导致z 方向出现压应变(εz＜0), 而ZZ (y)方向张应变(εy＞0)导致z 方向出现张应变(εz＞0), 由泊松效应导致垂直于面方向应变的不同抵消了面内应变效应的各向异性.

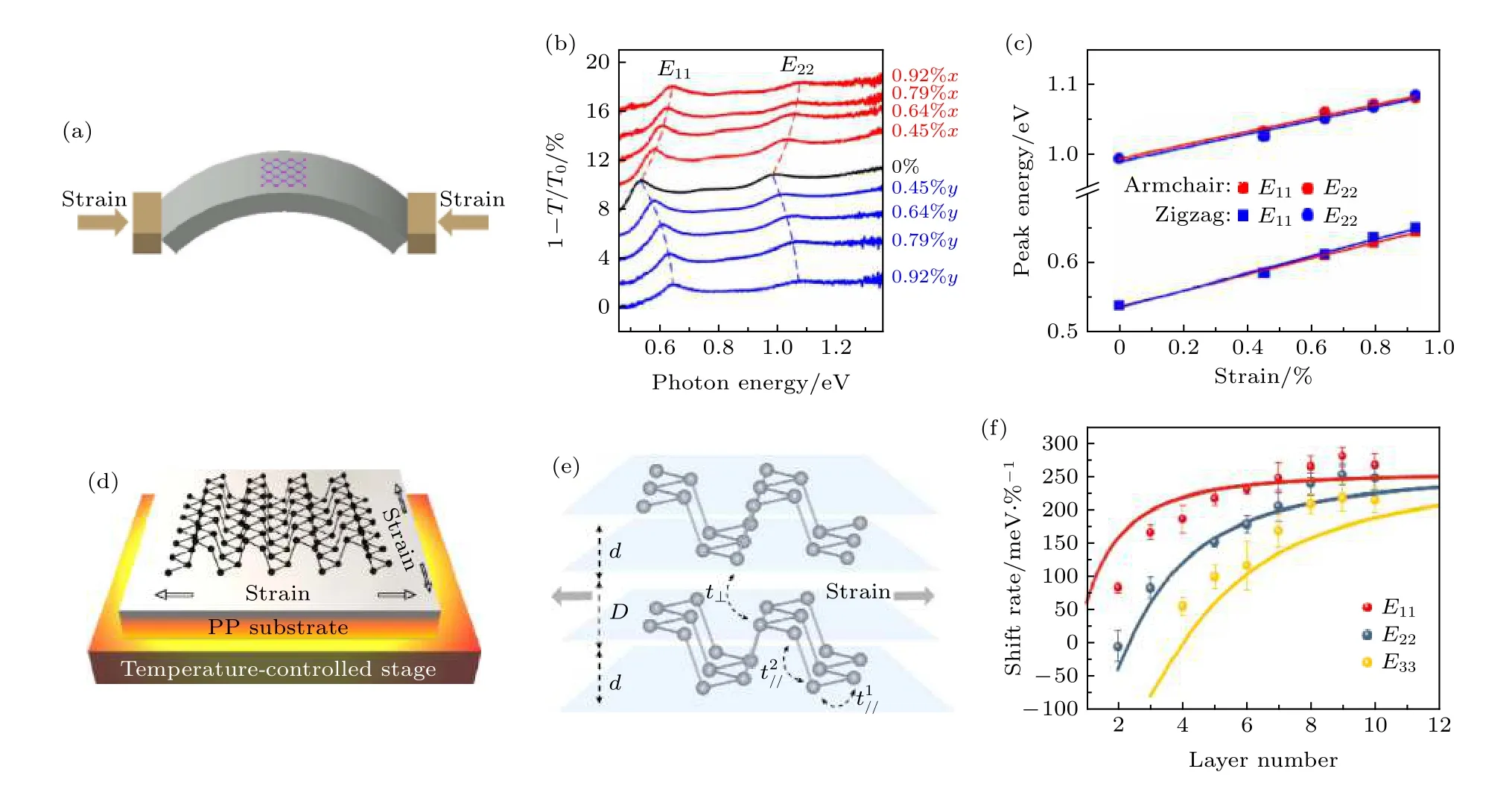
图7 应变效应 (a) 两点法对柔性衬底聚对苯二甲酸乙二醇酯(PET)施加单轴应变示意图[28]; (b)在不同张应变下6 层黑磷的消光谱, 其中x 代表应变沿着AC 方向, y 为ZZ 方向[28]; (c)不同的带间跃迁吸收E11, E22 峰位随应变的变化关系, 散点为实验数据点, 直线为线性拟合[28]; (d)通过加热或者冷却聚丙烯(PP)衬底实现施加双轴应变的示意图[57]; (e) 两层黑磷中垂直于面方向的跃迁参数的示意图[57]; (f) 2—10 层黑磷中E11, E22, E33 峰位的移动速率与层数间的关系, 散点为平均后的数据点, 曲线为紧束缚模型的拟合曲线[57]Fig.7.Strain effect: (a) Schematic illustration of two-point bending apparatus using a flexible polyethylene terephthalate (PET)substrate[28]; (b) extinction spectra of a 6 layers BP under varying tensile strains, with strain applied along AC (red) and ZZ (blue)directions[28]; (c) the E11 and E22 peak energies as a function of tensile strain, dots are experimental data and solid lines are linear fits[28]; (d) schematic illustration of the experiment set-up used for applying in-plane biaxial strain by heating or cooling the PP substrate[57]; (e) schematic illustration of the out-of-plane hopping parameter in bilayer BP[57]; (f) averaged shift rates of E11, E22,E33 peaks as a function of layer number in 2—10 layers BP, the solid curves are fitted to the data using the tight-binding model[57].

随后Huang 等[57]对2—10 层黑磷进行了的面内双轴应变调控研究.与单轴应变一致, 面内双轴张(压)应变使黑磷的吸收峰线性蓝(红)移, 并且峰位移动的速率为单轴两倍, 即双轴应变的调控能力更强.另外Huang 等还发现应变效应具有明显的层数依赖, 层数越薄带隙随双轴应变反而移动的越慢, 同时不同子带间吸收峰(E11, E22, ···)随应变的移动速率也是不同的, 高阶跃迁峰位随双轴应变移动得更慢(如图7(f)).实际上这与面内应变可调控的层间相互作用密切相关.通过一维紧束缚模型可以得到不同吸收峰随应变移动速率和层数N 及跃迁阶数n 之间的关系:

其中, ε 为双轴应变, h ,k 分别为单层的带隙和层间相互作用在双轴应变下的线性变化系数.可以看到该模型在整体上能够较好地描述这种层数、跃迁阶数依赖的应变效应(图7(f)).通过拟合得出1%的面内双轴应变可以带来近10%的层间相互作用的改变, 这是非常显著的变化.值得一提的是张应变下不同的带间跃迁的能量间距减小, 意味着层间相互作用减弱.而这是有违背于常识的, 因为通常情况下面内的张应变会导致垂直于面方向的压应变、层间距相应的减小, 而层间相互作用与层间距成反比, 进而导致层间相互作用的增大.事实上这种反常的现象起源于黑磷独特的褶皱面内原子结构, 通过紧束缚模型可以更清楚地看到这点.具体来说在紧束缚模型中层间相互作用的大小主要由跃迁参数的模决定[27], 而∝1/r2[58], 其中r 为连接的两个原子的间距(如图7(e)所示).张应变可以导致连接连接的两个原子的水平方向的间距增加, 同时态密度泛函理论(DFT)计算表明,1%面内双轴会导致层间距(D+d)减小0.031 Å(对应的垂直于面的泊松系数为0.5), 同时同一层中上下两个原子高度D 减小0.087 Å, 由此可知连接的两个原子的垂直方向的距离(d)反而增加了0.056 Å, 从而可以知道面内张应变可导致减小进而减弱层间相互作用.

3.2 电场调控

图8 电场效应 (a) 5 nm 厚黑磷的光电导(σ xx)实部随载流子浓度Ns 的变化情况[59]; (b)硝酸蒸汽掺杂前后9 层黑磷的消光谱, 黑色代表掺杂前, 红色为掺杂后[28]; (c)用来调控PL 的器件示意图, 该器件结构为氮化硼/黑磷/氮化硼并且用CVD 生长的石墨烯作为顶栅[62]; (d) 20 层厚黑磷在0—0.48 V/nm 电场下的PL, 其中点为实验数据点, 曲线为拟合曲线[62]; (e)双栅压调控的红外吸收测试器件示意图, 其中黑磷在Si/SiO2 衬底上(SiO2 厚285 nm)并蒸镀45 nm 厚的Al2O3 及5 nm 厚的钯作为顶栅[61]; (f)在黑磷不接电极(左图)和接电极(右图)时, 调控黑磷沿着AC 吸收强度的能力随栅压的变化[61]Fig.8.Electric field effect: (a) Evolution of real part of optical conductivity (σ xx) due to increasing carrier density Ns[59]; (b) extinction spectrum of a 9 layers BP before (black) and after (red) chemical doping through HNO3 vapor treatment[28]; (c) schematic illustration of the dual-gate hBN/BP/hBN device with CVD graphene as the top gate for tunable light emission[62]; (d) the measured (dot) and fitted (lines) tunable PL spectra of the 20 layers BP device under different displacement field from 0 to 0.48 V/nm[62]; (e) schematic illustration of infrared tunability device.BP was exfoliated on the 285 nm SiO2/Si substrate and then capped with 45 nm Al2O3 and 5 nm Pd as top gate[61]; (f) tunability of BP oscillator strength with a field applied to the floating device (left) and connect device (right), for light polarized along AC[61].

二维材料的厚度只有单个到几个原子层, 因此材料性质很容易受到垂直于材料表面的电场的影响, 通常可以通过栅压的方式来给二维材料施加垂直于面的电场从而来调控材料性能.对此Lin 等[59]计算研究了栅压对黑磷光学吸收的影响, 其中在垂直于面的电场中存在量子限制的弗兰兹-凯耳什(Franz-Keldysh)效应, 这会导致带隙减小从而使吸收峰出现红移; 同时栅压也会导致载流子浓度发生改变, 由莫斯-布尔斯坦效应(Burstein-Moss, 泡利不相容原理)导致吸收峰位的蓝移; 计算表明当载流子浓度不是很高时(＜ 2.75 × 102cm—2)量子限制的弗兰兹-凯耳什效应起主导作用并使得吸收峰位红移, 之后则是莫斯-布尔斯坦效应起主导作使得吸收峰蓝移(如图8(a)).另外由于垂直面的电场打破了黑磷原有的空间对称性, 选择定则不再严格成立, 使得E12/E21(第1/2 个价带到第2/1 导带间的跃迁)等杂化跃迁得以发生.Zhang 等[28]首次在暴露在空气的黑磷中观测到了杂化跃迁的吸收,这是因为空气中黑磷表面被氧化从而被掺杂, 而这种掺杂在空间上是非均匀分布的从而引入了垂直面的内建电场, 打破了原有空间对称性, 杂化跃迁吸收得以观测.进一步的Zhang 等又用氧化性更强的硝酸蒸汽对9 层的黑磷进行了掺杂(图8(b)),可以看到E11, E22峰位都出现了明显的红移(这与变坏过程中的峰位蓝移截然不同), 同时杂化跃迁吸收变得更强, 而这正是由更强的内建电场造成的.此后Whitney 等[60]通过对6.5 nm (13 层)黑磷加背栅压也观测到相同的实验现象.接着Sherrott等[61]在双栅压的器件中将量子限制的弗兰兹-凯耳什效应与莫斯-布尔斯坦效应区分开(如图8(e)),其中对于黑磷不接通电极的情况下(相当于黑磷悬浮在介质层中), 只会有量子限制的弗兰兹-凯耳什效应起作用, 而将黑磷接通电极后(即一般的FET工作情形)莫斯-布尔斯坦效应也会起作用.通过测试不同栅压下与0 电压下吸收谱的比谱(图8(f)),可以看到黑磷不接通电极的情况下施加负的栅压下后光学带隙出现红移同时杂化跃迁出现, 这符合量子斯塔克效应预期结果, 而栅压为正时则没有观测到相应变化, 对此Sherrott 等认为这是由栅压从负到正存在迟滞现象造成的; 而黑磷接通电极的情况下, 随着栅压增加由莫斯-布尔斯坦效应导致了带间吸收强度显著减弱, 然而吸收峰位并没有出现明显的蓝移.最近, Chen 等[62]通过将黑磷悬浮在介质层中施加栅压的方式(图8(c)), 研究了电场对发光性能的影响.如图8(d)所示, 随着电场的增加黑磷(厚度约为20 层)的发光波长可以从3.7 µm调至7.7 µm, 这也与之前的黑磷双栅压器件中电学测试观测到的带隙随着电场增加而减小相一致[63,64]; 另外还可以看到发光强度随着电场增加而降低, 这是由于电场增强导致了黑磷能带的倾斜加剧, 电子、空穴波函数空间分布被进一步分开从而降低了发光效率.

4 总结与展望

本文主要介绍了有关二维黑磷光学性质相关研究成果, 包括黑磷带间跃迁吸收、激子、发光等本征的光学性质, 以及外部微扰如应变、电场对光学吸收、发光带来的影响, 最后讨论了黑磷光学性质在空气中的稳定性.总之当前关于黑磷基础光学性质的研究已经取得了许多研究成果, 并在此基础上也有不少基于黑磷光电器件的应用研究, 如各向异性的光电探测器[65-67], 波长可调的红外激光器[68], 红外发光二极管(LED)[69]等.然而有关黑磷光学的研究仍然有很多重要的问题值得研究, 例如理论预测在黑磷中存在天然的双曲型色散的等离激元[70], 这种等离激元具有特定的传播方向和极高的态密度等特性, 从而具备极高的应用价值[71],然而至今仍然没有相关的实验研究报道; 除此之外二维黑磷本身为一种天然的量子阱, 子带间跃迁吸收从未被观测到, 而子带间跃迁吸收是量子阱中非常重要的性质, 其在长波波段的红外探测、量子级联激光器等有着重要应用价值[72]; 另外有关黑磷的范德瓦耳斯异质结、莫尔超晶格的研究也是屈指可数[73], 而在这些结构中往往都蕴含着令人意想不到的实验现象; 当然确保黑磷光学性质的稳定性也是黑磷走向应用前亟需解决的问题.