群体药动学研究方法及其研究进展
何春远,沈炳香,谢海棠
(1.六安市人民医院药学部,安徽 六安 237005; 2.皖南医学院附属弋矶山医院临床药学部,安徽 芜湖 241002)
群体药动学(population pharmacokinetics,PPK)是研究关于个体之间药物浓度差异的原因以及相关性的研究方法。患者的人口学信息资料、病理生理学和药物治疗学相关特征,如种族、年龄、体重和代谢等可以改变剂量-浓度关系[1]。PPK的目的是找出那些使其发生变化的可定量分析的病理生理因素,确定剂量-药物浓度变化的关系和程度,进而根据治疗指数的改变恰当地调整给药剂量。PPK把经典的药动学(pharmacokinetics,PK)基本原理以及统计学模型结合在一起,观察PK特性中存在的差异(固定性变异以及随机性变异),深入探查药物在人体内作用过程的群体规律、PK参数的统计分布及其影响因素。PPK被广泛应用于新药研发和临床实践中。本研究旨在通过调取国内外文献指南,综合最新内容,就PPK基本原理、研究方法及进展做简要概述,并着重阐述目前作为PPK分析“金标准”的非线性混合效应模型(nonlinear mixed effects modelling,NONMEN)法。
1 PPK概述
1.1 PPK研究的主要内容及步骤
PPK研究的内容及步骤见图1,其可简单地理解为输入(实验设计和收集数据)、计算(用NONMEM法进行数据分析,估算出PPK参数)和输出(分析和应用PPK参数)3个部分[2-4]。
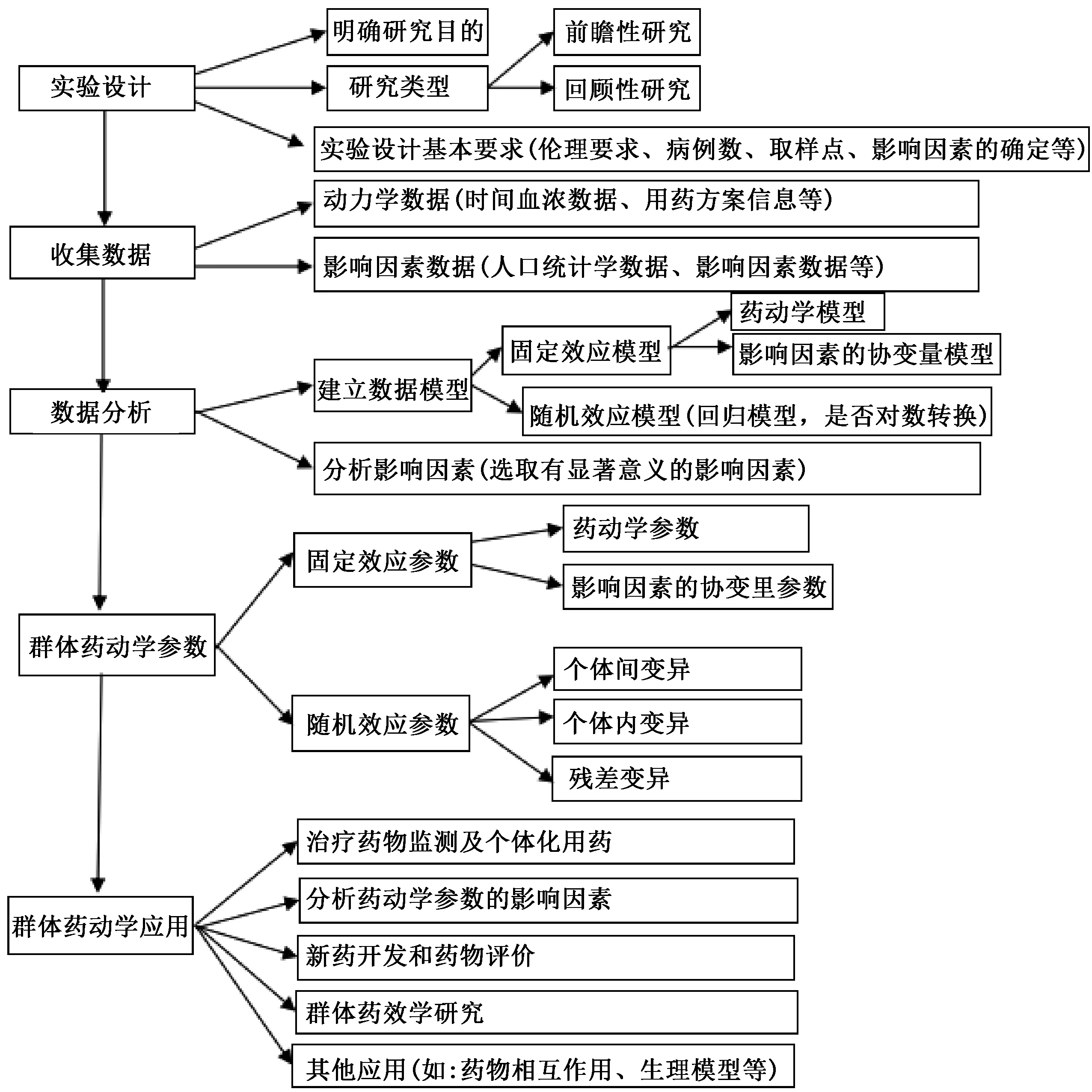
图1 PPK研究的内容及步骤Fig 1 Contents and procedures of population pharmacokinetics research
1.2 PPK的应用和优缺点
1.2.1 PPK的应用:近年来,PPK得到了迅速发展,主要应用如下。(1)在个体化给药方案的确定中,PPK研究方法具有非常重要的指导作用;(2)可以定量考察患者生理、病理等因素对PK参数的影响;(3)可与药效学(pharmacodynamics,PD)研究结合,即PPK-PD研究[5-6]。
1.2.2 PPK的优缺点:传统的PK研究通常涉及从健康志愿者中以固定间隔采集多个样本,PPK方法是在临床条件下研究药物体内处置的强力药理统计学分析方法,其具有优于传统PK建模方法的特点。(1)优点。①在患者而不是健康受试者中做研究,其结果更能说明患者群体的真实情况,更加具有临床意义;②采用稀疏数据也能进行药物研究,采样点少,患者更容易接受,适合临床研究的广泛开展;③精准估算个体间和个体内变异带来的误差,在误差的估算上相较于传统方法更为准确可靠;④精确考察患者的生理以及病理等因素对PK参数的影响程度,可为个体化给药方案的制定提供具体的参考意见;⑤可以在治疗期间进行灵活的适应研究设计;⑥建模软件应用广泛,基本原理和方法评价较为成熟(如NONMEM)[7-8]。(2)缺点。①PPK研究可在各类数据中进行,相较于传统PK研究对数据质量要求更高;②为了确保PPK研究的代表性,要求患者的病例数尽可能的足够大,病例数≥50例,每例患者采血点建议在2~4个点,如果协变量过多,则应适当扩大样本量和采血点数;③程序内语言算法较为复杂,理论性强、操作较复杂,需要经过专门培训才能够掌握;④群体方法常被误认为只是对一些设计不良的研究及其糟糕的数据进行牵强的合并[7-8]。
2 PPK研究基本方法
2.1 单纯集聚法
单纯集聚法是在忽略个体间的PK差异之后将所有个体数据进行合并后再进一步处理,好像数据全部来源于同一个体。故该方法不能有效区分个体间差异与随机效应。即使拟合过程观察到了观测值和拟合值间的残差误差和分布特征,但由于这类误差是由固定效应以及随机效应误差共同组成,所以不能进一步区分。而且在将数据合并后也将无法再计算每个个体的PK参数。因此,所得的数据没有得到充分的利用,浪费了部分数据,仅适用于个体数据较稀疏(例如每个个体只拿到1个血药数据)的情况[9]。
2.2 传统二步法
传统二步法在某种意义上与单纯集聚法相反。首先,认为个体的数据不能等同整体的部分数据,只能先采用各个体数据分别各自拟合,估算出每个个体的PK参数,然后根据每个个体参数计算出群体参数,如参数均值、几何平均值、方差和协方差等。传统二步法为计算PPK参数的传统方法,不需要非常大的样本量,但对于每例受试者都要进行密集采样。传统二步法也没有办法分别个体间和个体内误差,其求算出的是二者之和。这种局限只有在使用正式的PPK拟合方法时方能得以克服。有研究者指出,当残差误差可忽略时,标准两步法的效果较好,否则结果就可能出现偏离。而假定残差误差可以忽略实际上是一种不真实的状态。伴随着残差误差值的增大,标准两步法所算出的个体间差异也会出现稍许的偏大。这时就应当使用PPK的混合效应(固定效应和随机效应)模型(mixed effects modeling)方法进行分析[10]。
2.3 迭代二步法
迭代二步法是在已经得到的PPK参数的基础之上,首先建立一个近似的PPK预模型,把估算的近似参数视作所有患者个体化参数Bayes估算值,使用新的个体参数重新计算进而得到的群体参数作为新的近似群体值,然后重复估算步骤可以得出更为接近的个体参数,循环此步骤直至新老近似值无限接近。该方法可以利用全量数据、稀疏数据或混合数据,估算个体参数及群体参数。常用的软件包括USC软件包、PPAARM软件等[11]。
2.4 吉布斯取样法
Best等提出了一种更为常用的群体数据分析方法,根据群体模拟值可以估算重新组成每一参数的概率,或者适当简化以提供确切值或某个范围的数值,可用于较为广范复杂的模型,并且没有NONMEM法中的某些缺点[12]。
2.5 非参数法
参数法估算PPK参数是在假设未知参数的概率分布符合正态或对数正态分布的基础之上,而非参数法估算则适用于多种概率的分布。基于此中原理的算法包含非参数最大似然法、非参数最大期望值法。目前,非参数法尚处于理论研究阶段,缺乏实际应用的实例[13]。
2.6 NONMEN法
NONMEN法介于单纯集聚法与传统二步法之间,将经典的PK模型和个体间以及个体内变异的统计模型结合起来估算各种PPK参数。非线性混合效应建模(nonlinear mixed effect model,NLME)是由Sheiner在1977年正式提出的主要应用于临床监测稀疏数据的群体分析的数学方法和模型,适用于受试者样本或者采样点数据稀疏的情况。随后,Sheiner所在的美国加利福尼亚大学项目组开发了该分析方法的软件并命名为NONMEN,现在常使用NONMEM来描述软件程序,而不是NLME分析方法。 此外,“PPK”和“NLME方法”可互换使用。目前,国内外NONMEM软件应用均最为广泛,基本原理和方法评价最为成熟,并为美国食品药品监督管理局认可用于特殊的药物或患者药品临床PK评价。近年来,NONMEM法获得迅速发展,已被认为是PPK分析的“金标准”[14-15]。
2.7 NONMEM研究方法
2.7.1 NONMEM法建立PPK模型:固定效应模型可用于估算固定效应对PK参数差异的大小,模型结构包括线性、乘法、饱和和指示变量模型[16]。
例如,研究不同固定效应对清除率的影响:
(1)线性模型:用公式(1)表示。
(1)
(2)乘法模型:假如患者体重参数范围波动太广,且又与药物的清除有关系,可采用公式(2)表示。
(2)
(3)饱和模型:可用于描述具有最大效应的模型,例如在联合应用研究药物的抑制剂时,清除率公式可用公式(3)表示。
(3)
公式(3)中,θ2、θ3为二级结构参数,Cpss2是研究药物抑制剂的稳态浓度,这个模型形式上与米-曼氏模型一致。
(4)指示变量模型(分类变量模型):用公式(4)表示。
(4)
公式(4)中,HF(heart failure)表示心力衰竭指示变量,当患者有心力衰竭时赋值为1,没有心力衰竭时赋值为0,表示心力衰竭对清除率影响的大小。
可按照不同药物和群体特点,同时采用几种模型建模建立组合式固定效应模型,如公式(5)。
(5)
公式(5)中,CLcr表示患者的肌酐清除率,是常用来衡量肾功能的指标。
随机效应模型包含个体间变异以及个体内变异模型。个体间变异表示群体中个体之间PK参数的差异;个体内变异表示观测值无法解释的变异。由于个体间变异模型(L1)效应描述的是个体间的参数差异,这些值在个体中的观测结果通常是常数,因此受到个体水平的影响。个体间变异模型通常由加法模型、比例模型(CCV)、指数模型建模:
(1)加法模型:个体间的参数差异可以用加法模型来表示。个体参数(Pi)是群体典型值(P)和个体间随机效应(ηi)的函数,该加法模型表示为公式(6)。
Pi=P+ηi
(6)
描述药物最大药效PD参数(Emax)的模型,可以用加法模型编码,如公式(7)。
TVEMAX=THETA(1);Population Typical Value
EMAX=TVEMAX+ETA(1);Individual Specific Value
(7)
公式(7)中,TVEMAX表示Emax中的群体典型值,ETA(1)以随机变量η表示,其均值为0,方差为ω2,表示为η=N(0,ω2);每个个体具有唯一的η值,因此个体具有唯一的Emax值。在上述例子中,与较大的Emax值相比,较小的Emax值具有较大的百分变异系数(%CV),如公式(8)。
(8)
由于加法模型在参数的所有值上定义了一个恒定的标准差,所以,当参数被认为是较低的值(即较低的平均值)时,将具有比在较高值时更大的%CV。换言之,变异的幅度随着参数值的增加而减小。因此,使用该模型时,%CV不是恒定的。
(2)比例模型:该模型可表示为公式(9)。
Pi=P(1+ηi)
(9)
相比之下,CCV模型保持相同的相对幅度的变异,但是绝对幅度随着建模参数值的增加而增加。CCV模型可以被编码如公式(10)和公式(11)。
TVKe=THETA(2)
Ke=TVKe+TVKe×ETA(2)
(10)
或
TVKe=THETA(2)
Ke=TVKe×(1+ETA(2))
(11)
在该模型中,标准差与参数值的增加成正比。因此,在参数值的范围内,参数的变异具有恒定的%CV。
(3)指数模型:指数模型可能是个体间模型最常用的模型。这些模型描述了正态分布的参数的变异性。具有指数结构的Ke参数的模型如公式(12)所示。
(12)
TVKe=THETA(1)
(13)
Ke=TVKe×EXP(ETA(1))
(14)
因变量观测值(Y)与模型预测值(F)之间的差异定义了观测值的残差或不明原因的误差,以随机变量ε表示,其均值为0,而方差σ2,表示为ε=N(0,σ2)。误差元素(εi,j)呈现为数据集中每个非缺失的因变量。L2误差分布可以与随机L1变量相似的函数形式来建模:
(1)加法模型:残差可以用不依赖于其他因素的单一方差表示。误差被简单地添加到预测中以便解释与观测的偏差,且不考虑预测值或其他因素,如公式(15)。
Y=F+εi
(15)
公式(15)中,Y为浓度观测值,F为浓度的模型预测值,εi为个体内变异。
加法RV模型可以在NONMEM中编码如公式(16)、公式(17)和公式(18)。
Y=F+ERR(1)(适用于个体间模型和个体内模型)
(16)
或
Y=F+ETA(1)(仅适用于个体间模型,例如L1 error)
(17)
或
Y=F+EPS(1)(仅适用于个体内模型,例如L2 error)
(18)
随着时间变化的浓度误差见图2。当预测浓度低或预测浓度高时,误差差异变化不大或者当观测到的浓度在窄范围内波动时,如在稳态下的谷浓度收集,或以恒定速率静脉注射期间的稳态浓度,用加法模型更合适。

图2 加法模型中浓度随时间变化曲线Fig 2 Time-varying curve of concentration in addition model
当误差的大小随着预测的大小而变化时,RV可以用CCV表示,误差的差异与当前的模型预测成正比,如公式(19)。
Y=F(1+εi)
(19)
该模型以NONMEM编码如公式(20)、公式(21)所示。
Y=F+F×ERR(1)
(20)
或
Y=F×(1+ERR(1))
(21)
使用ERR(……)、ETA(……)或EPS(……)的相同替代表达式如前所述适用于的加法模型。图3可以代表CCV模型中药物浓度随时间变化的曲线。实线是浓度预测值,虚线表示取决于在给定浓度下的实际观测值的上限和下限。因此,在较低的预测浓度下,误差差异相对较小;而在较高的预测浓度下,误差差异相对较大。
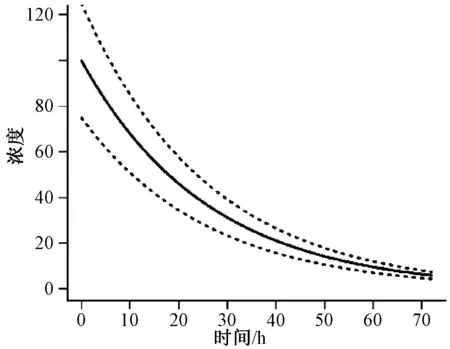
图3 CCV模型中药物浓度随时间变化的曲线Fig 3 Time-varying curve of drug concentration in CCV model
通常在群体PK建模中使用的RV模型结合了前面描述的2个模型,包括加法模型部分和比例模型部分。当预测浓度低时,加法模型部分占主体地位;而随着预测浓度的增加,比例模型逐渐占主体地位。这个模型可以用简单的2个随机变量表达,如公式(22)。
Y=F+F×EPS(1)+EPS(2)
(22)
公式(22)中,EPS(1)是与随机效应模型中的比例模型相关的随机变量,而EPS(2)是随机效应模型中加法模型部分。
2.7.2 群体模型的验证:PPK模型验证主要分为内部验证法和外部验证法。内部验证法使用从总数据中抽取的验证组数据,或用重取样技术验证建立的模型。又可分为数据分割(data splitting)、重新取样法(re-sampling techniques)及蒙特卡洛法(Monte Carlo simulations)。外部验证法是采用模型组建立模型,用另一组新数据重新建模,并比较两个模型对新数据的预测结果[17]。(1)数据分割法(data-splitting)。将得到的数据随机划分为两组,即建模组和验证组。因模型估算的准确性取决于样本的大小,故验证后应把两组数据综合在一起作为一个整体,最后估算出PPK参数[18]。(2)交叉验证法(cross-validation)。交叉验证法是在相对复杂的情况下获得几乎无偏差估计预测误差的方法。每次将样本的90%建立模型,然后对其余10%进行模型验证,用这种方法对所有数据逐一进行验证,观测其预测效果。交叉验证算法的优点是建模的数据库较大[19-20]。(3)刀切法(Jacknife)。刀切法在1958年被Tukey所介绍,每次从原样本中剔除1个样品,得到样本为n-1的新样本,称为Jacknife样本,总共n个,计算每个样本的参数值,称为Jacknife估计[21-22]。(4)自举法(bootstrapping)。自举法应用于统计程序分析精度不能评定的复杂问题。通过对原始数据进行重新采样,生成人工样本,计算每组数据参数,并根据参数分布判断模型是否可靠,进行与原始样本相关的推理[23]。
3 总结
相较于传统PK研究方法,PPK能够更方便地解释各种因素造成的变异,能够为临床个体化用药提供重要参考。个体化用药就是根据患者特点,针对个体差异而制定出合理的给药方案,进一步提高疗效,减少药物毒副作用。NONMEM法综合考量固定效应和随机效应等各种混杂因素,实现了个体化用药。较常采用的方法是先通过NONMEM法计算出PPK参数,再结合Bayesian反馈法估算出个体PK参数,设计个体化给药方案,如对治疗窗窄的药物的个体化给药、个体差异大的药物的个体化给药、联合用药的个体化给药以及特殊人群的个体化给药等。考虑到数据提供的信息量大小,研究可能会纳入不同的模型类型。本研究对研究方法进行了深入探讨,旨在为PPK学者提供清晰的思路和方法。
PPK研究方法具备传统PK研究方法所不具备的优势,能够解释各种因素造成的变异,能够为个体化用药提供重要参考。目前,NONMEM法是PPK研究的“金标准”。伴随着个体化用药治疗在我国迅速发展,PPK的应用范围也越来越广泛,现在已成为临床PK研究的重要方法。

