基于次表面散射的肝脏高真实感实时渲染的研究与实现

吴德道，刘小平

(1.南昌大学信息工程学院，江西 南昌 330031；2.景德镇陶瓷大学，江西 景德镇 333000；3.卡尔顿大学系统与计算机工程系，渥太华 加拿大 K1S 5B6)

1 引言与研究背景

光线在虚拟手术中的场景视觉表现，不仅在软组织表面发生反射，还会产生散射，并可能进入软组织内部，光线在这类材质的物体中传输会经过一次或多次的散射，最终可能从某个难以预知的出射点射出，也可能在软组织内被吸收。通常人们称这种光线发生散射、吸收及衰减的现象为次表面散射(Sub-Surface Scattering，SSS)。为了表现这类半透明物体的次表面散射，众多学者进行了一系列的研究。准确渲染半透明材料如皮肤表皮需要求解次表面散射方程，一种常用解析方法是用扩散理论[1]。Munoz[2]提出基于单独图片的方法模拟BSSRDF，实现了一部分半透明材质的真实感模拟。Jensen等[3-4]利用扩散理论得到了BSSRDF的偶极扩散近似，Donner和Jensen[5]将偶极近似扩展到一个多极模型，该模型能更好地模拟多层材料中的光传输，因此比较适合包括皮肤等半透明材料外观的视觉呈现。他们利用一种近似多层材料扩散剖面的方法并使用测量到的散射参数计算了一个完整的三层人体皮肤模型。利用扩散剖面，模拟次表面散射相当于根据剖面的精确形状将入射漫射光散射到邻近位置。这将呈现一个逼真的软组织半透明的外观。但是偶极子和多极子模型对于实时应用来说代价消耗巨大。

D’Eon[6，7]观察到偶极子和多极子模型预测的扩散剖面可以近似为高斯分布的加权和，从而可以实时计算次表面散射。因此，每个扩散剖面都可以近似为高斯卷积的线性组合。次表面散射方程中的BSSRDF实际上表达了与径向对称不可分离扩散剖面R(r)的二维表面卷积[7]。在纹理空间扩散[8-9]中，通过将辐照度光栅化到纹理中，对该纹理应用卷积操作，并将结果映射回网格来模拟这个过程。虽然纹理空间扩散近似提供了实时视觉呈现，但存在一些缺点。如运行缓慢，为每一个半透明的物体在每一帧上计算一系列的辐照度卷积纹理代价相对昂贵，屏幕上有多个对象的情况下性能迅速下降。为了解决这些问题，Jimenez[11-12]提出将扩散近似的评估从纹理空间转化为屏幕空间，并将二维扩散核分解为两个一维核，避免了卷积纹理计算的开销，实现了实时呈现效果。

针对人体软组织在真实环境光照下的散色、透射及次表面散射不确定的特点，本文提出了采用表面反射和次表面散射两种光照模型组合的解决方法来模拟人体肝脏的真实光照表现。首先采用Kelemen/Szirmay-Kalos高光BRDF[13]计算镜面反射，这是对Cook-Torrance反射模型的近似[14]，考虑了来自各个方向的入射环境光，除了从阴影映射中提取单个样本外，还检索了最近的四个样本。然后对所有深度测试的结果进行双线性插值，以确定光源可见样本的百分比。为了实现实时呈现效果，利用扩散剖面对辐照度进行二维卷积，近似为高斯和并将二维扩散核分解为两个一维核，避免了卷积纹理计算的开销。通过结合D’Eon等提出的变体纹理空间[6-7]和Jimenez等的屏幕空间半透明技术[15]实现肝脏组织边缘较薄处透射的效果。实验结果表明，能逼真地模拟出人体肝脏的视觉外观，且能保证模型在复杂渲染算法情况下的实时效率。

2 相关理论

在软组织次表面光照效果的研究中，本文主要利用了求解次表面散射方程来准确渲染，以下是对有限介质传输方程[16]的简化：

(1)

当积分同时在A区域(被渲染表面上的点)和入射方向w上时，S(p，q，v，l)是一个双向表面散射反射分布函数(BSSRDF)。这个函数将BRDF扩展到考虑光从表面进入的位置以外的其他位置的光，并给出了从位置p辐射到观察方向v的光在位置q处从l方向入射光的比例：

(2)

通过使用BSSRDF而不是BRDF，我们能够获得一个柔和的软组织外观。求解次表面散射方程的一种常用解析方法是用扩散理论[1]。Jensen等[3-4]利用扩散理论得到了BSSRDF的偶极扩散近似，该近似仅依赖于材料的散射特性，任意两点p和q处的菲涅耳透射率Ft以及这两点之间的距离存在以下关系：

(3)

上式中R(*)是材料的扩散剖面，菲涅耳透射率描述了光从一种介质传输到另一种介质的量。1/π项描述的是射入的光量，它在p点周围的半球上向一个方向v反射。Donner和Jensen[5]将偶极近似扩展到一个多极模型并能模拟多层材料中的光传输，因此比较适合皮肤外观的视觉呈现。利用扩散剖面模拟次表面散射相当于根据剖面的精确形状将入射漫反射光散射到邻近位置而产生柔和半透明的外观，但偶极子和多极子模型对于实现实时效果的系统带来巨大的负担。

(1)D’Eon[6-7]观察到偶极和多极模型预测的扩散剖面可以近似为高斯分布的加权和，从而可以实时计算次表面散射。从扩散剖面R(r)到高斯和的映射需要为k个高斯项找到合适的权值wi和方差vi：

(4)

上式中高斯项定义如下：

(5)

常数1/2πv保证每个高斯函数都有单位总扩散响应，即高斯函数下的总面积等于1：

(6)

因此，每个扩散剖面都可以近似为高斯卷积的线性组合。D’Eon等发现四种高斯分布足以对大多数单层材料进行建模，并对Donner和Jensen的高加索皮肤三层模型提出了六个高斯项分布拟合，如表1所示，每个面的高斯权值之和为1，因为皮肤的颜色是由颜色映射定义的，而不是嵌入到扩散面本身。D’Eon等描述了红色通道的六个高斯信号也可以准确地用于绿色和蓝色通道，从而降低成本。

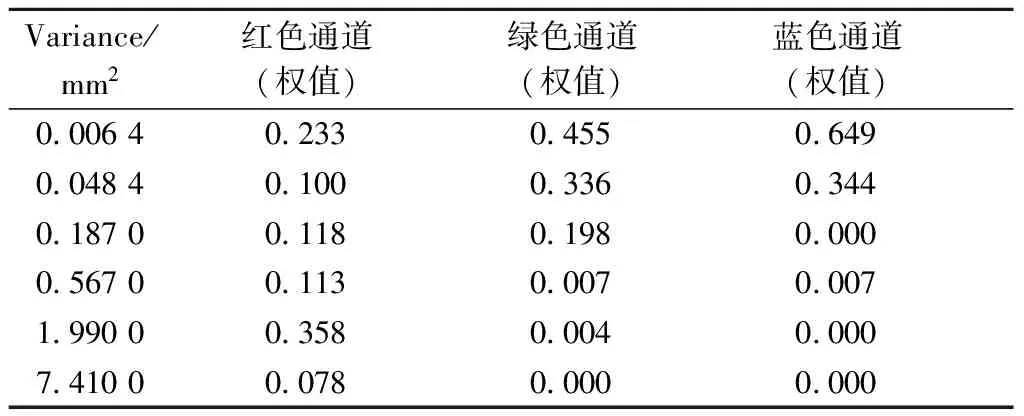
表1 六高斯项拟合三层皮肤模型[6]

次表面散射方程中的BSSRDF实际上表达了与径向对称不可分离扩散剖面R(r)的二维表面卷积[7]。在纹理空间扩散中[8-9]，通过将辐照度光栅化到纹理中，对该纹理应用卷积操作，并将结果映射回网格来模拟这个过程。理想形状的模糊过滤器完全符合材料的扩散剖面。虽然精确的扩散剖面可以直接通过昂贵的二维卷积来计算，但是d’Eon等利用高斯函数的可分离性将其简化为一组代价更小的一维卷积。通过将不可分离的扩散剖面表示为高斯和，可以对辐照度卷积进行分层和分离评价，得到一系列具有越来越宽模糊核的卷积辐照度纹理。这些卷积纹理的加权和然后近似的卷积辐照度的原始扩散剖面。结合采样的反照率和次表面散射将产生最终的半透明材料色调。

(2)次表面散射可以由反射和透射组成。当入射光进入材料的距离足够远，其中的一小部分会从材料的另一端出去时，就会发生透射。材料的确切性质将决定光在材料中传播的距离和扩散。因为皮肤有相对较高的吸收因子和平均散射因子，所以它既不是透明也不是不透明，而是半透明的。有些光可以通过耳朵和鼻子等皮肤的薄层甚至人体肝脏边缘，但只能以高度扩散的形式通过。在离线渲染领域，目前已有各种将半透明效果纳入材质呈现的方法中，Donner和Jensen推导出了计算透射剖面和反射剖面的方程[5]。对于实时渲染，一种考虑透射的方法是使用修改后的阴影贴图。Jimenez实现了屏幕空间半透明技术[15]，该技术基于d’Eon提出的变体纹理空间[6-7]。

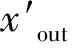
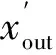
(7)

卷积核R(r)的计算与前面一样使用高斯和近似：

(8)

其中d=mcosθ是物体的局部厚度(如图1)。

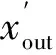
3 肝脏高真实感实时渲染方法

对肝脏进行图像三维重建后所得的数字化模型，如图2所示，可观察到对比实物原图2(a)，重建三维模型图2(b)～(d)表面色泽真实感表现相对较不自然，这是由于模型表面纹理贴图是图像序列加权平均得到的，且模型表面不含任何光照信息。为复原真实肝脏所具有的光感表现，首先分析半透明材质中最显著的次表面散射特性，但是直接用BSSRDF模型进行模拟计算效率太低，故为保证实时渲染效率，采用[18]所提到的多层BRDF模型叠加的方法来模拟半透明模型具有的次表面散射表现。通过分析可知，肝脏组织主要具备高光、表面散射及边缘组织较薄处透射的物理光学表现，所以，本文提出了两层光照模型线性叠加的方式来模拟半透明高光效果。

3.1 基于物理的反射

Cook-Torrance模型是一种基于物理的BRDF，它利用微面元理论来确定物体表面的粗糙度，并考虑了菲涅耳反射、微面元定向、微面间的相互遮挡和吸收光线。在d’Eon和Luebke[6]之后，利用Kelemen/Szirmay-Kalos高光BRDF[13]计算镜面反射，这是对Cook-Torrance反射模型的近似[14]，简化了几何项(遮挡)，使BRDF实时渲染效果更好：

(9)

上式中l是光的方向，v是视场方向，h′=l+v;h=h′/|l+v|，h′是非归一化半矢量，h是归一化半矢量。D(n，h)是贝克曼正态分布函数[19]，它描述了面向h的微面部分，有助于光从l方向反射到v方向：

(10)

上式中α是n和h之间的夹角，k是粗糙度系数，而F(v，h)是菲涅耳反射项，它描述了每个微面反射的光线数量。为了提高渲染器的性能，采纳D’Eon和Luebke[6]的建议，预先计算并渲染Beckmann分布到一个8位的纹理映射中，然后在运行时读出。利用Schlick’s[20]计算菲涅耳反射项：

FSchlick(F0，l，h)=F0+(1-F0)(1-(l·h)5)

(11)

除了镜面反射，Kelemen/Szirmay-Kalos BRDF还包括漫反射部分。D’Eon和Leubke[6]描述了一种使用预先计算的纹理来增加节能的方法，而视觉效果可根据应用程序的不同来评估。扩散分量实际上一般被用作非常粗略的物体次表面散射近似[3]。本文选择使用Lambertian漫反射，因为之后将由一个次表面散射着色器的修改。使用Kelemen/Szirmay-Kalos高光BRDF，从l方向的单光源出发，在点p处向视场方向v的高光强度修改为：

LSpec(p，v)=kSpecDBeckmann(k，n，h)

(12)

上式中kSpec为全局高光强度因子，IL(p，l)为来自光源L的入射光，本文使用了聚光灯，因为它较好地代表了现实生活中的灯光并有一个较简单的等式：

IL=cL·fattenuation·ffalloff

(13)

上式中cL为以RGB值表示的光的颜色，函数fattenuation和ffalloff根据到光源的距离确定光强，漫反射方程与高光反射方程相似：

Ldiff(p，v)=calbedoIL(p，l)n·l

(14)

上式中calbedo是从提供漫反射物体表面颜色的颜色纹理映射中采样的RGB值。最后，表面点的镜面反射和漫反射直接为计算对每个光源的求和。

由于高光的亮度是由两个因素来决定的：高光强度kSpec和粗糙度系数k。通过从一个双通道高光纹理中采样这些量并允许它们在模型的表面变化，从而提高高光部分的逼真度。此外，采样一个法线贴图来扰动位于p点的表面法线n，如式(14)所示。像高光贴图一样，法线贴图的添加允许我们改变表面的粗糙度，这样就可以表现出软组织表面更多的几何微观特征。

3.2 改进的实时次表面散射及透射模拟

虽然纹理空间扩散近似提供了实时视觉呈现，但也存在一些缺点。比如运行缓慢，为每一个半透明的物体在每一帧上计算一系列的辐照度卷积纹理仍然代价相对昂贵，导致在屏幕上有多个对象的情况下性能迅速下降。为了解决这些问题和其他方面的考虑，Jimenez等提出将扩散近似的评估从纹理空间转化为屏幕空间。在最近的工作中，他们提出了一种可分离屏幕空间扩散近似方法。本文的渲染器实现了[11-12]中描述的次表面散射技术。因为该方法为实时物体表面呈现提供了一种高性能的解决方案，可以很容易地集成为一个后处理着色器。

3.2.1 简化可分离次表面散射的实现

为了实现实时呈现效果，扩散剖面对辐照度进行二维卷积，近似为高斯和。Jimenez等[11-12]提出了一种新的方法，将二维扩散核分解为两个一维核，避免了卷积纹理计算的开销。定义一个可分离的一维滤波器S[x，y]，将二维扩散核S分解为代价更少的水平和垂直一维核S[x]：

S[x，y]≈S[x]×ST[y]

(15)

上式中，[x，y]是样本位置，ST[y]是S[y]的转置。由于扩散剖面的径向对称性，方便利用转置滤波器。滤波器S[x]定义为初始扩散剖面p[x]的函数，并将其参数化，使其更适合于精确的目标扩散剖面：

(16)

宽度k定义了以世界空间为单位的次表面散射核的全局宽度。强度t指定有多少扩散光穿透表面，因此将被次表面散射所改变。它是原始未滤波图像与模糊图像的混合因子。f定义了梯度随距离变化的形状。大的衰减使形状更宽，而小的衰减使形状更窄。宽度是标量，在R、G、B通道上是均匀的，而强度和衰减根据每个通道来定义。

使用可分离扩散核的渲染简化为在渲染的漫反射图像上应用一个双通卷积滤波器。为了与一维核函数s[x]进行卷积，需要对核函数进行离散化。这是通过计算中心位置附近的样本偏移量X，以及基于初始轮廓、强度和衰减参数的每个样本的谱权W来实现的。考虑到渲染的实时性和对视觉的影响程度，本文使用9个样本。样本偏移量X可以通过在核范围内均匀地间隔来计算，然后用指数函数对其进行修正，从而使越靠近中心的样本越具有高的重要性。核范围定义了采样扩散剖面p[x]时x的最大范围，从而影响离散化过程的精度。对于n个样本的初始等间距偏移量集计算为：

(17)

其中r是核函数范围的一半。比如n=9，r=2得到：

{-2.0，-1.5，-1.0，-0.5，0.0，0.5，1.0，1.5，2.0}

计算核权值W的集合要求我们首先计算修改后的剖面p[x]=R(r)，其中r=x∈X是样本偏移量。剖面在每个采样点返回每个通道的漫反射系数。如前所述，对于三层皮肤模型，采用六高斯和的红色通道进行离散化，并通过强度和衰减参数进行参数化。以下是一个直接实现的函数：

(18)

其中r=x，高斯项k=6，各个高斯权值wi和方差vi由以下集合定义(可参见表1中红色通道的权值和方差)：

wi∈{0.233，0.100，0.118，0.113，0.358，0.078}

vi∈{0.0484，0.187，0.567，1.99，7.41}

第一个高斯函数可以考虑直接表示散射光，由于它的方差很小，因此可以忽略，这样高斯项减少到k-1。实际高斯函数的计算公式如下：

(19)

这类似于d’Eon等描述的高斯函数，但现在包含了半径r除以衰减f，允许高斯函数的形状发生变化。较大的衰减值使高斯曲线变宽，较小的衰减值使高斯曲线变窄。每一个颜色通道衰减值的范围从0到1并且为防止除0加上了一个ε=0.001。

通过计算内核偏移量和内核权值可以使用可分离的子表面散射像素着色器将实际的滤波器应用于屏幕空间图像；可见算法1。内核的最终大小(以世界空间单位为单位)与像素的投影表面积有关，后者取决于像素的深度和表面方向。在第4行和第5行，根据当前像素的深度确定内核的比例。这个值可以看作像素的大小，通过将到图像平面的距离除以深度缓冲区中存储的深度值d得到：

(20)

其中θfovy是用摄像机观查场景的垂直视域。计算这个角的一半的余切就得到了从相机原点到图像平面的距离(见图3)。对于位于图像平面上的像素，scale为1.0，随着距离的增加而减小。在第6行计算采样期步长，它是scale与全局散射宽度w以及一个二维方向向量的乘积，该方向指向水平方向(1，0)或垂直方向(0，1)取决于这是过滤器的第一遍还是第二遍，然后除以样本偏移量的半范围r，使其在[0，1]范围内。

算法1可分离次表面散射像素着色器伪码

function：ssssps(texcoord，kernel，width，nsamples，range，fovy，direction，colormap，depthmap)

1：Initialize result=float4(0，0，0，1)

2：color←colormap.Sample(point，texcoord)

3：depth←depthmap(point，texcoord).r

4：projdist←1.0/tan(0.5* radians(fovy))

5：scale←projdist/depth

6：step←scale*width*direction/range

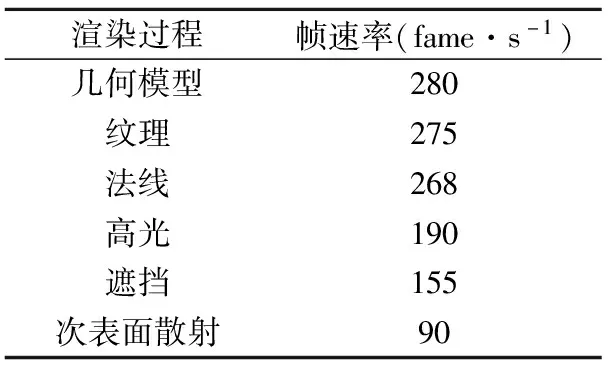
7：fori++

8:if i is nsamples then

9:result.rgb←result.rgb+color.rgb*kernel[nsamples/2].rgb

10:end if

11：offset←texcoord+kernel[i].a*step

12：tap←colormap.Sample(linear，offset)

13：d←depthmap.Sample(linear，offset).r

14：s←saturate(300.0*projdist*width*abs(depth-d))

15：tap←lerp(tap，color.rgb，s)

16：result.rgb←result.rgb+kernel[i].rgb*tap.rgb

16：end for

16：return result

17：end function

计算实际的扩散卷积需要积累每个样本的贡献。对于中心样本，只需要计算从颜色图中提取的皮肤颜色和中心内核权重的乘积。其他样本的颜色贡献是通过对颜色图中邻近的纹理进行采样来确定的，从而有效地将邻近位置的颜色渗到着色器处理的目标像素中。线性抽样是用来提高图像质量的，增加样本的数量会得到更逼真的效果。算法1是分离的次表面散射像素着色器的伪代码，当距离大于扩散剖面时，用原始像素颜色对样本的贡献进行线性插值，消除了相邻样本与卷积中心之间的较大深度变化。这将减少屏幕空间中距离较近但物体空间较远的位置之间不必要的颜色渗出，迫使卷积更精确地跟随3D模型的表面。在算法1第14行300.0的修正值是一个经验确定的量。表面渲染器应用可分离的子表面散射像素着色器作为漫反射图像的后处理过滤器。第一遍计算水平方向上的卷积，第二遍计算垂直方向上的卷积。由于次表面散射只适用于漫反射组件，为了避免模糊，在最终渲染过程中，将之前计算的高光组件分离并添加进来。

3.2.2 透光率计算

Jimenez等[15]提出了一种计算屏幕空间扩散的半透明度的解决方案，其工作原理类似于纹理空间方法。在屏幕空间中面临的主要问题是物体背面表面点的信息更少(从相机的角度来看)，而半透明问题相当于求解下面的方程：

(21)

穿过物体的距离d仍可以从阴影贴图中得到。然而，在屏幕空间中无法获得面向光表面上xin点处的入射辐照度E(xin)。因此引入了一些假设来近似辐照度。

首先，将x点处的法线替换为阴影处的反向法线：Nin=-Nout。其次，前面的反照率αout(从相机的视角)是用来近似后面的反照率。这是因为皮肤的表面反射率通常不会有很大的变化。此外，假设光照面的辐照度近似为局部常数，使得x点附近的所有采样点与x点本身(E(xin)=E)值相同，且：

E=αoutmax(0，Nout·L)

(22)

其中L是光向量。根据这个假设有：

(23)

利用d’Eon的高斯和近似，考虑到高斯信号具有单位总扩散响应，M(x，y)简化为(推导见文献[15])：

(24)

为了降低计算复杂度，d近似为s(见图1)，通过将点xout转换为光空间并从该点的存储深度值中减去而得到。以下是一个基于物理的函数T(s)，它将光强度的衰减与物体内部移动的距离联系起来：

(25)

这个函数可以预先计算并存储为衰减纹理，或者直接在着色器中计算。在表面渲染器中选择后者，因为直接计算通常比访问纹理内存快并节省内存。

实现半透明的像素着色器伪代码如算法2所示。前6行伪代码计算了xin(d1)处的深度值和xout(d2)处的深度值，并得出它们的差值等于距离s。使用阴影映射进行深度值近似导致在将背景像素投影到对象上时，对象边缘的精确度不够。在从阴影映射查询深度值时(第3行)，为确保所有采样点都在观察视角，样本位置在表面法线方向上少量收缩(第2行)。在阴影映射中找到正确的样本位置需要手动执行透视图转换(第3行)。光透射距离是由两个参数决定的，这两个参数决定了透射的强度。首先是散射滤波器在世界空间单位上的宽度。这个参数之前用于次表面反射滤波器。另外一个参数，半透明因子是一个从0到1的值，它直接控制透射效应的强度。距离8.25的经验值使得透光率变得明显。第7～10行使用表1的高斯和近似计算距离s对应的颜色。将辐照度E近似为上文所述，通过将阴影点处光源强度乘以M(x，y)=ET(s)得到总透光度，对给定像素的每个光源均是如此获得总透光度。

算法2透光率计算伪码

function：transmittance(worldpos，normal，lightdir，shadowmap，viewproj，farplane，spotlight，albedo)

1：Initialize Ts=float3(0，0，0)

2：pos←float4(worldpos-0.005*normal，1.0)

3：lightpos←mul(pos，viewproj)

4：d1←shadowmap.Sample(linear，lightpos.xy/lightpos.w).r*farplane

5：d2←lightpos.z

6：s←(8.25*(1.0-Translucency)/ScatterWidth)*abs(d1-d2)

7：ss=-s*s

8：for i++<6 do

9:Ts←Ts+float3(redi，greeni，bluei)*exp(ss/vari)

10：end for

11：E←saturate(0.3+dot(-normal，lightdir))

12：return E*Ts*spotlight*albedo

13：end function

4 实验结果与分析

实验环境配置为CPU为Intel core i5 5200，内存4 GB，显卡为AMD Radeon R5 M320的便携计算机上进行了渲染实验；使用3ds Max 2014版本作为渲染工具，Shader语言为CG。实验用例皆为实际的肝脏经图像三维重建后得到的数字化模型。

4.1 实验渲染结果分析

第1组实验对象是图2(a)在经图像重建后得到的肝脏三维几何模型，如图2(b)、(c)、(d)所示，实验中首先得到的是如图4所示真实肝脏经重建后所得贴图，之后利用本文方法进行渲染实验，在渲染过程中，每一步的绘制实验图如图5所示。

通过上图肝脏模型渲染的过程，在添加纹理后只有二维平面效果，而增加法线贴图后才有了立体效果，通过表面高光以及配合的环境光的表现使得模型具有了自然光照的属性特点，增加阴影自遮挡效果使得模型表面有了坑洼的增强立体感，然后通过算法1实现的模型次表面散射使其具有了柔和的人体组织视觉特点，最后通过算法2实现光在肝脏较薄和边缘处的透射以高真实感的呈现其半透明的视觉效果。

4.2 实验结果对比分析

本文提出的方法是分两层光照模型叠加模拟最终的结果，通过第一组最终实验结果如图5与采用3Dmax渲染的模型如图2(b)、(c)、(d)的比较，采用本文提出的方法渲染的肝脏模型更接近现实如图2(a)。而对重建模型漫反射层的比较如图6第二组实验所示，由此看出经典方法需配合环境光照来表现更多的模型细节。

4.3 渲染效率分析

第三组实验如表2展示出在肝脏模型面片数为3968的情况下利用本文渲染方法达到的帧速率。通常12 frame·s-1的帧速率为人眼所达到实时交互的最低的帧速率，而如表2中本文渲染速率，当采用次表面散射方法渲染模型时，其渲染的帧速率依然可以在90 frame·s-1左右，为人眼实时最低速率的7.5倍。所以本文实验方法保证了实时渲染的需要。综合图5实验可得，本文方法可实现基于次表面散射重建肝脏模型高真实感实时渲染。

表2 依次增加的渲染过程及所对应的帧速率

5 结语

本文在实现人体肝脏图像三维重建后的真实感光照实时渲染问题上，提出利用表面反射和次表面散射光照模型结合的方法模拟表面高光及散、透射表现。通过从一个双通道高光纹理中采样光强度和粗糙度系数并允许它们在模型的表面变化，从而提高高光部分的逼真度。此外，采用法线贴图、阴影遮挡贴图以及位移贴图来改变肝脏表面的粗糙度以表现更多的几何微观特征和增强立体视觉。采用Kelemen/Szirmay-Kalos高光BRDF计算镜面反射并考虑了来自各个方向的入射环境光，使得渲染的肝脏模型更接近自然光照的视觉呈现。为了实现实时呈现效果，利用扩散剖面对辐照度进行二维卷积，近似为高斯和并将二维扩散核分解为两个一维核，避免了卷积纹理计算的开销。通过结合纹理空间和屏幕空间半透明技术实现肝脏组织边缘较薄处光线透射的效果。实验结果表明，本文方法能逼真地模拟出人体肝脏的视觉外观，且能保证模型在复杂渲染算法情况下的实时效率。