基于多车道加权融合的短时交通流预测研究
杨春霞,秦家鹏,王 庆,李欣栩
(1.南京信息工程大学 自动化学院,江苏 南京 210044; 2. 江苏省大数据分析技术重点实验室,江苏 南京 210044; 3.江苏省大气环境与装备技术协同创新中心,江苏 南京 210044)
0 引言
交通流预测是利用人们行为产生的历史交通流数据进行分析,是智能交通系统(Intelligent Traffic System, ITS)中的重要构成部分。多年来,在缓解交通拥堵、降低资源浪费等方面发挥重要作用,一直深受运输领域学者的关注[1-2]。
利用历史交通流数据隐含的特性进行短时交通流预测已经取得重要进展。从早期的统计模型到最近的深度神经网络模型,很多学者[1]关注的是交通流长短程时间尺度上的相似性,如杨春霞等[3]引入交通流周时间尺度的相似性;傅成红等[4]构建深度学习回归机模型,学习交通流时间序列的深度特性等方法都取得了较好的效果。另一方面,也有学者关注空间尺度上的关联性,如常刚等[5]利用区域路网交通流的时空依赖性,进一步提高了短时交通流预测精度。然而,几乎未见有人关注同一路段不同车道上交通流的复杂关联特性。多车道关联性是指在多车道公路中受人们驾驶行为的影响,各个车道间交通流存在复杂的关联性,如何剖析这种关联特性是本研究重点关注的一个问题。
近年,深度学习因为能够深入挖掘数据特性而逐渐受到各领域学者的关注[6-7]。在智能交通领域,Vythoulkas等[8]首次提出使用系统识别和人工神经网络来预测城市道路网络的交通状况。Hochreiter等[9]提出长短期记忆网络(Long Short-Term Memory,LSTM)模型,该模型能够捕获交通流数据中长期依赖性的内在特征;Cho等[10]通过简化LSTM结构构造了一种门控循环单元(Gated Recurrent Unit,GRU)模型,该模型能够适当减少训练时间,LSTM/GRU模型在流量预测领域都取得了很好的效果[11-12]。然而LSTM/GRU仅能处理单向信息流动而无法学习上下时间信息关联。Schuster等[13]提出双向循环神经网络(Bidirectional recurrent neural networks,BiRNN)模型,该模型可以通过正负时间方向上学习交通流的上下关联。Huang等[14]用BiRNN来预测交通流,试验表明该模型能够有效捕捉交通流上下关联。双向长短时记忆网络(Bidirectional Long Short-Term Memory,BiLSTM)受BiRNN的启发在LSTM基础上增加反向的LSTM,拼接正负时间方向上LSTM的结果从而获得上下关联交通流信息,并且在流量预测领域取得了很多成果[15-16]。综合分析,采用BiLSTM模型进行短时交通流预测,提出一种考虑多车道加权融合的BiLSTM短时交通流预测模型,通过最大信息系数分析不同车道交通流和聚合交通流的关联程度,构建BiLSTM模型对各车道交通流和聚合交通流分别进行短时交通流预测,并对预测的各车道交通流和聚合交通流加权融合为最终预测交通流。对比以往传统预测模型的一些研究工作,本研究所提的多车道加权融合模型预测精度更高,并且对多数多车道路段均适用。本方法可以有效学习交通流数据前向、后向时间关联特性,能够融合各车道交通流对聚合交通流的关联影响,进一步提高短时交通流预测效果。
1 关联判定
不同车道间交通流受人驾驶行为[17]和驾驶规则影响存在某种程度时空关特性。时空关联性是研究空间对象随时间的变化规律,反映时空数据在时间和空间上的关联,本研究采用最大信息系数(Maximal Information Coefficient, MIC)[18]来衡量不同车道交通流关联程度。
最大信息系数主要是利用网格划分法和互信息进行计算,它能够广泛度量变量间的依赖关系。将各车道交通流和聚合交通流训练数据作为一个有限的有序对数据集D={(Xi,Yi),i=1,2,…,n},将Xi的取值范围分成x段,将Yi的取值范围分成y段,得到若干个x×y形式的网格,即称为G。公式定义为:
MI*(D,x,y)=maxMI(D|G),
(1)
式中,D|G为数据D在x×y网格G进行划分,式(1)表示在不同划分方式中计算的最大化信息。然后将不同划分下得到的最大归一化MI值构成特征矩阵,特征矩阵定义为M(D)x,y:
(2)
设划分x×y网格的上限为B(n),效果最好时B(n)=n0.6,那么最大信息系数定义为:
(3)
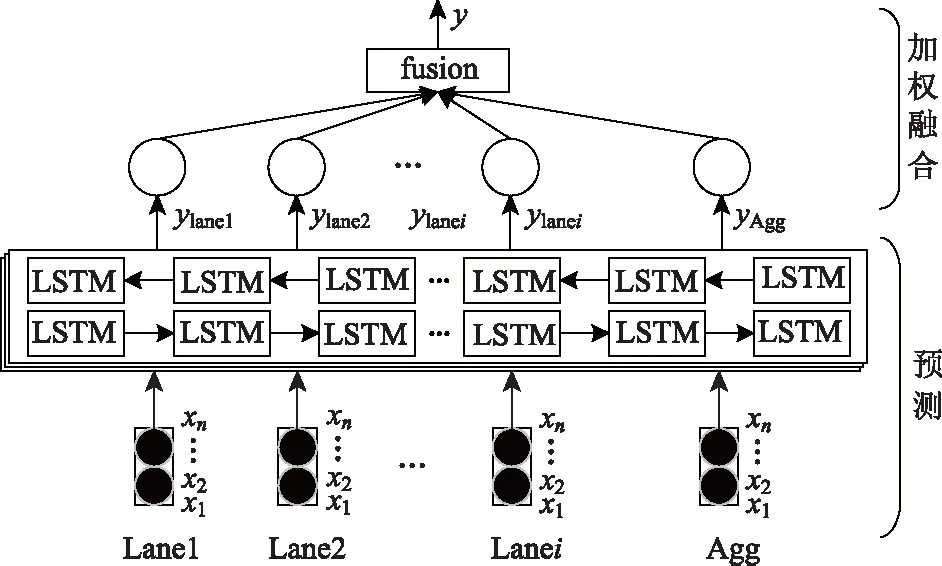
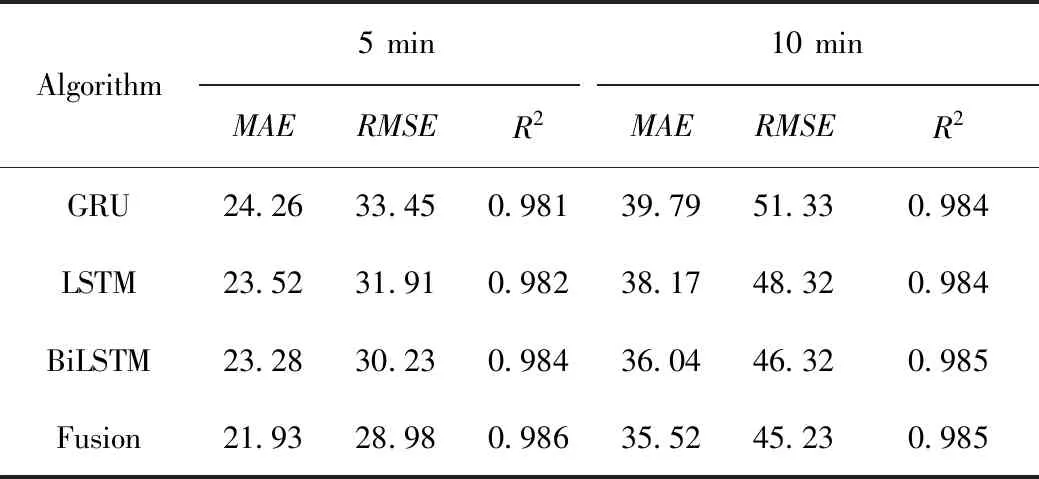
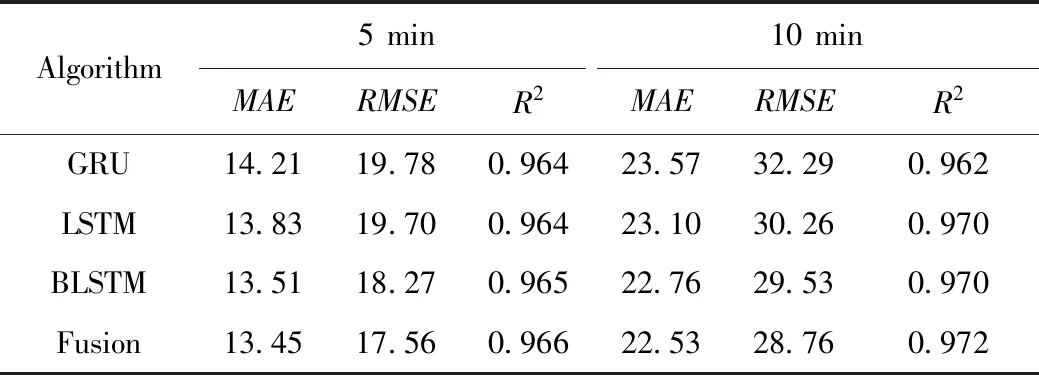
式中,xy LSTM模型[9]属于一种前向训练模型,仅能捕捉前向历史交通流数据的长期特性,但是交通流数据不仅依赖于过去信息,且和驾驶人未来航程规划存在关联,BiLSTM能够从前后方向处理并整合数据,这更符合人的旅行习惯。本研究选用BiLSTM模型学习交通流上下关联性。图1给出LSTM模型框架。 图1 长短时记忆预测模型Fig.1 Long short-term memory prediction model LSTM各个门的状态满足以下公式: ft=σ(Wf.[ht-1,xt]+bf), (4) it=σ(Wi.[ht-1,xt]+bi), (5) ot=σ(Wo.[ht-1,xt]+bo), (6) (7) (8) ht=ot⊗tanh(Ct), (9) BiLSTM从历史数据的前向和后向训练数据,在模型隐藏状态输出前拼接前向和后向学习的特征,其公式可表示为: (10) (11) (12) 岭回归(ridge regression, RIDGE)是一种惩罚线性回归,对处理多元数据占有一定优势,它通过在线性回归损失函数后引入惩罚L2正则化项,恰当地解决了线性回归过拟合问题,岭回归损失函数为: (13) 对此公式求导,表达如下: (14) 令公式(14)等于0,根据给定的X和y,求得系数矩阵W: W=(XTX)-1XTy, (15) 式中X为给定的输入数据,其给定形式表示X=[x0,x1,…,xM]T,加权拟合权重参数为w=[w0,w1,…,wM]T,X与w对应相乘输出数据y=[y0,y1,…,yN]T。 多数公路是由多车道构成的,而且每个车道间交通流和聚合交通流受旅行者驾驶行为的影响存在很强的关联性。基于此,本研究提出基于多车道加权融合预测模型,该模型分为两个模块:预测模块和加权融合模块。图2给出了该模型框架。在预测模块,假设各车道交通流和聚合交通流分别作为独立的子模块,对各子模块构建训练数据集,如取Lane1的训练数据集X={x1,x2,…,xn}输入BiLSTM模型中进行训练预测,其预测结果为yLane1。同法,对剩余车道交通流和聚合交通流做出预测。 图2 多车道加权融合预测模型Fig.2 Multi-lane weighted fusion prediction model注:图中Lanei表示i车道的交通流,Agg表示Lanei的聚合交通流。 在加权融合模块,整合预测模块预测的各车道交通流和聚合交通流,然后作为不同变量输入岭回归中得到各变量的融合权重,其加权融合公式为: (16) 式中,wAgg,yAgg为聚合交通流的权重及预测值;wLanei,yLanei为i车道交通流的权重及预测值;yfusion为yLanei与yAgg的加权融合交通流。 本算法使用Adam优化函数来更新参数,采用交叉验证法和Dropout函数来提高算法的测试精度,通过调整参数使算法不断逼近期望输出。多车道加权融合预测模型步骤如下: (1) 样本分类。取样本数据Lanei与Agg作为不同子模块分别划分为训练数据和测试数据。 (2) 样本预处理。对各子模块训练数据X={x1,x2,…,xn}分别归一化处理。 (3) 初始化网络状态。包括神经单元的细胞状态C0、隐藏状态h0,将步骤(2)处理的数据按子模块分别输入第一层BiLSTM神经元。 预设N=20,M=3,L=6,图2和图3分别为随机选取单个SU的信道和功率策略概率演化过程.从图中可以看出经过200次迭代后,用户信道选择概率向量由初始值{1/3,1/3,1/3}最终收敛到{0,0,1},并维持恒定不变.同时用户在6个功率等级上的选择概率也同样的表现,结论与定理1和定理2相符. (5) 判断向前层和向后层的LSTM神经单元是否学习结束,没有结束,继续步骤(3)。 (6) 根据式(4)计算ht,保留ht并进入下一层BiLSTM神经单元计算中。 (7) 重复以上步骤计算下一层BiLSTM神经单元,BiLSTM神经单元训练完后采用Dropout函数随机丢失一部分特征,以防止过拟合,最后通过FC全连接层进行加权整合输出,分别计算出各车道交通流和聚合交通流预测值yLanei,yAgg。 (8) 加权融合。把交通流预测值yLanei与yAgg作为不同变量输入岭回归法中,通过训练得到各变量的融合权重,然后通过公式(16)加权融合得到最终预测值yfusion。 采用经典的均方根误差(RMSE)和平均绝对误差(MAE)作为度量指标判断预测结果的性能,以及选择R平方(R2)用于判断预测值与真实值的拟合程度。其中RMSE亦称标准误差,其与L2范数很类似,易忽略较小误差值,对异常值很敏感;而对于较小误差的累计,MAE比较敏感。RMSE,MAE,R2的公式如下: (1)均方根误差: (17) (18) (3)R2的指标: (19) 同文献[3]一样,试验数据来自美国加州高速公路的性能测量系统(Caltrans Performance Measurement System, PeMS)数据库平台。平台数据最小间隔时间为 5 min,能够根据试验需要聚合以5为倍数时间间隔的交通流数据。本研究选择“1108717”与“407323”两个主干道观测站的交通流数据来验证试验的可靠性,取其中一个观测站数据如图3所示,Agg表示聚合交通流,Lanei表示i车道交通流,从图3明显看出Agg与Lanei存在趋势相似性。文献[3]给出证明,同“周几”交通流拟合度要优于以工作日为尺度的交通流数据。基于此,本研究对原始交通流按同“周几”划分周时间尺度数据集,然后采用最大信息系数分析周尺度多车道交通流与聚合交通流两两间的关联性。 图3 各车道交通流与聚合交通流Fig.3 Traffic flow in each lane and aggregated traffic flow 如表1所示,表示了Agg与Lanei的关联度,为了使试验更具有严谨性,假设Aggi表示同“周i”的聚合交通流,对Aggi与Lanei进行全面的关联性分析。从表1给出的最大信息系数来看,Aggi与Lane3的关联性平均系数高达0.908,属于强相关,反面表明Lane3被Aggi可替代性较强;而Aggi与Lane5的关联性均值最低为0.762,从另一方面看出Lane5被Aggi可替代性较弱。总的来说Aggi与Lanei都具备较强的关联相似性。由这种关联性初步判定,Lanei各车道的交通流趋势有助于辅助分析Aggi交通流的走势。 表1 聚合交通流与各车道交通流间的关联系数 本研究试验平台处理器是INTEL(R)Core(TM)i5-4460CPU@3.20GHZ 3.20GHz,操作环境为Windous10 64位,内存16 GB,试验基于Keras深度学习库,Keras库模型搭建迅速且高效,能够满足多数神经网络需求。本研究模型多层隐含层单元数均设为64,输出节点设为1,试验参数根据试凑法选择最优参数,设置时间步长为12,训练迭代600次,学习率0.001,损失函数为mse,在调参时每试验5次以验证调参的可靠性。本研究在全连接层输出前加入了Dropout层,以防止模型过拟合。图4为验证集和Dropout层调参时的性能变化,当随机选取其中3 d作为验证样本,且Dropout设为0.3时,模型表现最优。 图4 不同参数的性能比较Fig.4 Comparison of performances of different parameters 根据Lanei和Agg分别进行归一化处理。对Lanei和Agg而言,在训练模型时,若xN为当天某任意时刻交通流,将前一段时间N时刻和当天N-1,N-2,…,N-12时刻的交通流数据输入模型,当天N时刻的交通流数据作为目标输出。选择2月8日—8月23日交通流数据作为训练样本,预测30日N时刻的交通流。 为验证本研究所提预测方法的可靠性,下面依次从两个不同类型观测站以5,10 min间隔时间交通流分析本研究所提方法的预测效果。表2中给出了LSTM,GRU与BiLSTM模型和本研究所提方法对五车道“1108717”观测站交通流的预测结果评价指标。如表2所示,在5 min时间间隔内,各模型的预测误差都很小,GRU,LSTM与BiLSTM模型的MAE,RMSE值分别为24.26,33.45,23.52,31.91,23.28,30.23。其中,GRU模型预测误差最大,这是因为在学习数据特征时,GRU从上层只有一个输出传输到下层,降低了对较长时间数据特征的记忆能力;LSTM模型相对GRU增加了一个记忆细胞,能够记录较长时间的数据依赖特性,因此在预测结果上有一定提升;BiLSTM模型在LSTM的基础上融合了前向与后向数据特征的关联性,进一步提升了预测结果。本研究所提方法的MAE,RMSE达到了21.93,28.98,相对BiLSTM模型预测误差更小,因为本方法融合了BiLSTM的优点,能够学习数据的上下时间关联,并且在另一方面考虑了聚合交通流与各车道交通流的关联性。在10 min时间间隔数据进行各模型试验,结果表明所提预测方法预测误差也是最小的,预测效果最优。以上初步说明在预测聚合交通流时,适当考虑各车道对聚合交通流的关联性有助于提高交通流的预测精度。 表2 “1108717”观测站的预测误差对比 图5对比了多车道加权融合预测方法与试验中表现最好的BiLSTM模型预测效果。从图中预测曲线和测试曲线的走势来看,显然本研究所提方法预测曲线与测试曲线拟合效果更好,特别在一些异常值拟合方面本研究所提方法更具有优势,这是因为所提方法在预测时不仅考虑数据的上下时间依赖性,还融合了聚合交通流对各车道交通流的辅助依赖。在绝对误差方面,本研究方法的绝对值基本低于75 veh,而BiLSTM模型的预测绝对误差较多介于75~100 veh之间,在交通流特征学习上表明本研究所提方法更优,反方面也表明未考虑多车道交通流关联的BiLSTM模型在波动剧烈的数据上,学习能力比较弱。试验结果表明考虑了Lanei趋势与Agg趋势的关联性,能够更好地学习交通流的突变值,对提高交通流预测精度有一定帮助。 图5 BiLSTM与BiLSTM-RIDGE模型预测结果对比Fig.5 Comparison of prediction results between BiLSTM and BiLSTM-RIDGE models 表3为各模型在三车道“407323”观测站交通流的预测误差对比。可以看出,“407323”观测站总体预测误差低于“1108717”观测站,这是因为五车道交通流量略多于三车道,随着交通流量的增多会增加数据的剧烈变化程度。 表3 “407323”观测站的预测误差对比 从表3各模型预测误差对比方面,本研究所提预测方法在5,10 min时间间隔交通流的预测误差中表现最优。但是本研究方法预测误差相对未考虑各车道交通流关联的模型并没有降低很多,因为每个车道交通流量少,数据波动小,使模型能够更好地学习交通流的特性,随着车道数的减少,各车道交通流对聚合交通流的辅助作用也会有一定降低。综合来说,本研究引入多车道与聚合交通流的关联性,有助于提高交通流预测精度,同时也具有一定的鲁棒性。 研究了多车道交通流与聚合交通流的关联性,提出一种将多车道关联与BiLSTM模型相结合的短时交通流组合预测模型,本方法适用多数多车道观测路段。首先对试验的交通流数据进行分析,发现车道交通流与聚合交通流存在相似关联性。然后考虑这种关联性,构建双向长短时记忆模型分别训练预测各车道交通流与聚合交通流,加权融合各部分预测结果。最后在两种观测站交通流进行试验验证,本研究所提预测方法明显优于BiLSTM等模型预测结果。试验证明,引入各车道交通流与聚合交通流的相似关联性能够进一步提高交通流预测精度,对缓解交通拥堵提供更高效的助力。 交通流变化受天气、交通事故、上下游交通流等因素的影响,也会因车道限速而迅速变化。接下来将进一步挖掘交通流与以上因素的依赖性,利用这种依赖性来提高交通流预测性能。2 模型原理
2.1 双向长短期记忆模型理论

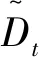
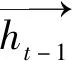
2.2 岭回归算法
2.3 基于多车道加权融合的BiLSTM预测模型
2.4 加权融合预测算法
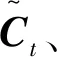
2.5 试验评价指标
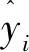
3 试验分析
3.1 数据来源与分析
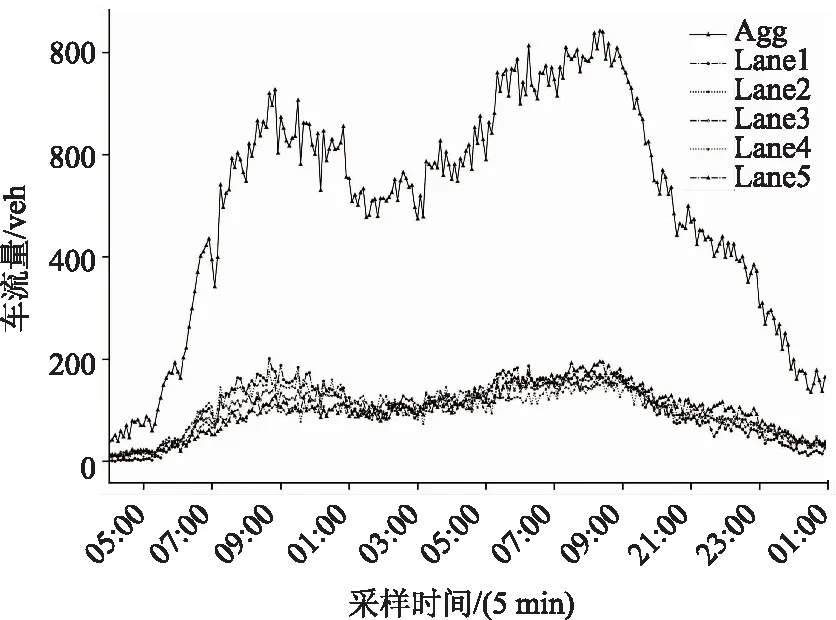

3.2 试验分析及评价


4 结论

