基于梯度修正的改进分水岭模型在细胞分割中的应用*

肖月，李朋伟

(太原理工大学信息与计算机学院,晋中 030600)

1 引 言

细胞分割是细胞分析处理技术的重要环节之一，如何获取更加准确和完整的分割结果显得尤为重要。近年来，研究人员提出了许多有效的分割算法，关涛等[1]采用形态学滤波与自适应直方图均衡增强图像，然后在图像内容与直方图分布关系的基础上，利用经验因子加权Otsu寻找自适应阈值的宫颈细胞分割方法；夏海英等[2]提出了一种改进的简单线性迭代聚类(simple linear iterative clustering, SLIC)分割算法，利用SLIC算法得到超像素区域并与原图像融合后进行标记，再由最大相似准则合并区域获取宫颈细胞分割结果；林丽群等[3]利用形态学去噪与分数阶微分对图像进行预处理增强，采用分水岭算法与最小生成树算法结合的融合算法对粘连血细胞图像进行分割。然而，阈值分割只考虑图像的灰度信息，且对噪声敏感，容易造成分割结果不均匀；区域分割算法适应性低，单独使用效果差；图论分割算法复杂、计算量大，不易操作。因此，目前尚无一种通用的细胞分割算法能使细胞图像达到完美的分割效果。

Vincent和Soille在1991年首次提出了基于淹没的分水岭分割算法[4]，该算法结构简单、抗噪声能力强，并且可以得到连续封闭且位置准确的目标轮廓，适用于细胞图像的分割。但传统分水岭算法易受噪声影响出现过分割现象，因此，研究人员提出了许多改进的分水岭算法。朱逸婷[5]将标记的分水岭法与局部信息模糊C均值聚类算法(fuzzy local information c-means, FLICM)结合在一起，通过聚类算法进行区域合并来改善过分割现象。孟少波等[6]利用小波分解变换对形态学梯度图进行分解去噪，并通过阈值处理重构二维小波，经小波二次分解去噪后的分水岭变换极大地减少了过分割的现象。郭小梅等[7]利用分水岭方法将图像分割成许多区域一致的像素块(超像素)，基于超像素重新构建原图像后再作标记，减少了算法过程中的待处理信息量，提高了运算速度及图像分割效率。

针对以上问题，我们提出了一种基于Canny算子梯度修正的优化分水岭算法，并用于细胞图像的分割。首先对图像HSV颜色空间的各个通道分量利用Canny算子提取梯度，然后利用图像信息熵确定各个分量在原始梯度中的权值，通过加权拟合形成最终的梯度图像；对加权梯度图进行基于开闭的滤波重建操作以平滑梯度图像中的伪极小值，之后区域化梯度图像，通过设定阈值对各个区域分别提取梯度极小值联合构成前景标记图，再由前景图像获取背景分割脊线并记为背景标记；最后利用强制极小值标记技术对重建梯度图和前景、背景标记图对梯度进行修正，将修正后的梯度图用作分水岭算法求出最终分割结果。

2 传统分水岭算法

传统分水岭算法的操作对象并不是图像本身，而是针对图像梯度进行处理。算法基于拓扑学原理，将图像梯度视作地貌高度，通过模拟降水(或淹没)过程使每个局部的最低点处汇集成一个集水盆地，当两个邻近的集水区要汇合时，在汇合处筑造堤坝，全局建成的堤坝即为分水岭。分水岭算法依据图像的梯度变化将图像迅速地区域化，为分析提取图像的局部特征提供更多可能。该算法对图像的微弱边缘响应灵敏，可以得到单一、封闭且强连续性的图像边缘，因此，适合细胞图像的分割提取[8]。

由于分水岭算法灵敏度高、响应性好，其对图像噪声以及图像的不规则变换也异常敏感，具体表现为图像灰度细节的微弱变化或是噪声均能使图像的局部极小值增加，造成分割后的区域过多而产生过分割现象；噪声会直接影响图像梯度，对含噪声的梯度图像直接分割会造成图像轮廓偏移或混叠。这些均给图像的分析带来困扰，因此，如何获取表达图像信息完整且不含噪声的梯度图像，是优化分水岭算法的一个重要解决方案。

本研究算法流程见图1。

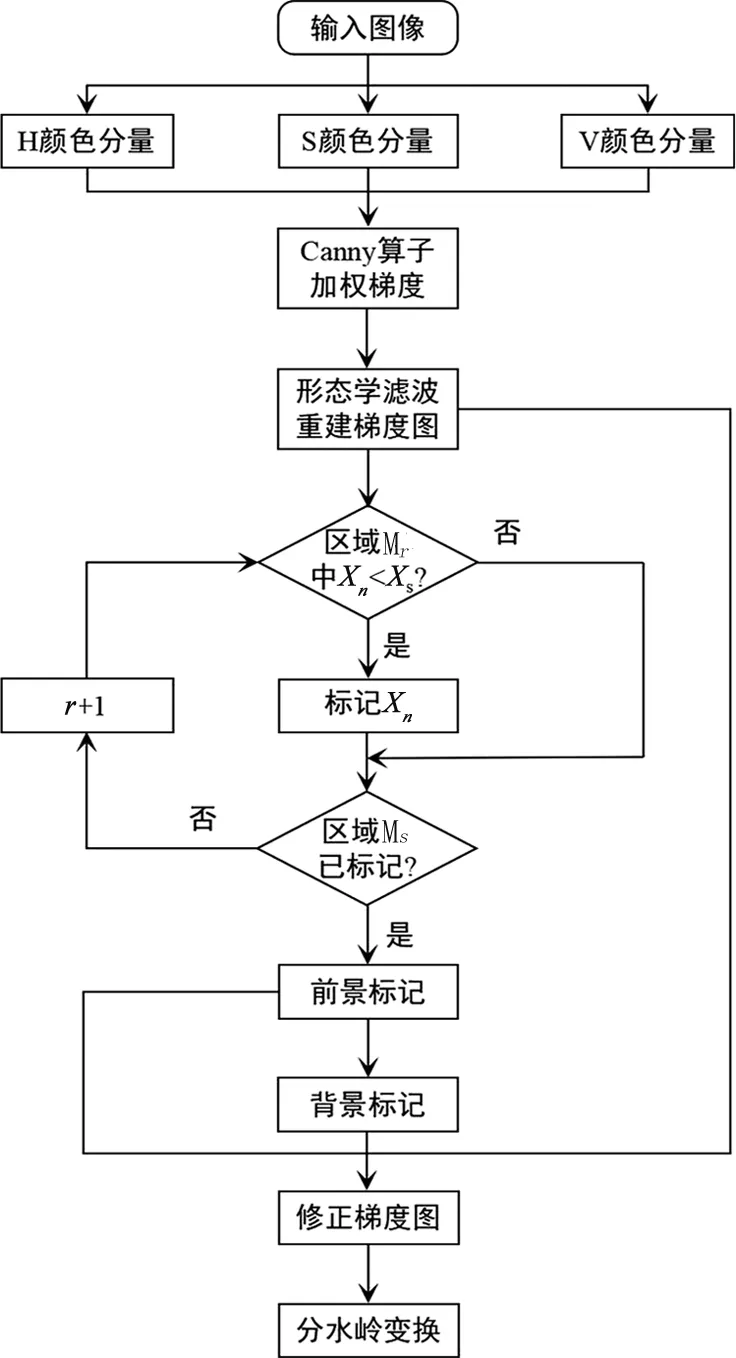
图1 改进分水岭算法的流程图

3 改进分水岭算法

3.1 Canny算子提取梯度

Canny算子是目前应用最多的边缘检测算子，具有良好的抗噪性能，同时又能保证边缘检测的完整性[9-10]。Canny算子是针对灰度图像的边缘检测设计的，而彩色图像直接转为灰度图像时，会导致部分颜色特征丢失，使检测结果出现边缘断接或虚假连接。故本研究算法选择在图像的HSV颜色空间上进行梯度提取，该颜色模型由色调(H)、饱和度(S)、明度(V)三个通道组成，各个分量之间关联性较弱，互不影响。所以HSV颜色模型的抗干扰能力强，在对图像边缘进行检测时稳定性较高。

算法中利用Canny算子对HSV空间的三个颜色分量分别提取梯度gH(x,y)、gS(x,y)、gV(x,y)，之后由三个颜色分量所含信息熵的比值确定各分量梯度的权值，然后通过加权拟合形成最终的梯度图，见图2。具体操作过程如下：

(1)提取H、S、V各通道分量的梯度：由Canny算子对fH(x,y)、fS(x,y)、fV(x,y)三个通道分量的图像提取梯度，主要分图像平滑、梯度幅值计算、非极大值抑制和边缘连接四个步骤进行，得到各颜色通道的梯度图像gH(x,y)、gS(x,y)、gV(x,y)；

(2)计算各分量梯度图的权值：图像信息熵是图像特征的集中反映，表示图中平均信息量的数量，根据不同颜色通道的图像特征不同，利用信息熵作为量化三个分量图像携带信息量的参数，以确定各通道分量的权重。图像二维熵不仅可以反应一维灰度信息分布的聚集特征，还可以联合像素邻域灰度均值构成二元序列组表达灰度特征的空间分布关系。假设图像像素的灰度值表示为i，取其邻域像素的灰度均值记为j(邻域范围由图像大小决定)，共同构成二维灰度特征的元组序列(i,j)，其中，0≤i≤255，0≤j≤255，l(i,j)表示该灰度元组出现的频次，其出现的概率为(图像尺寸为m×n)：

(1)

统计图像所有灰度级出现的概率，则图像的信息熵I(x,y)可以表示为：

(2)

由此可得H、S、V三个颜色分量的图像熵值分别为IH(x,y)、IS(x,y)、IV(x,y)。

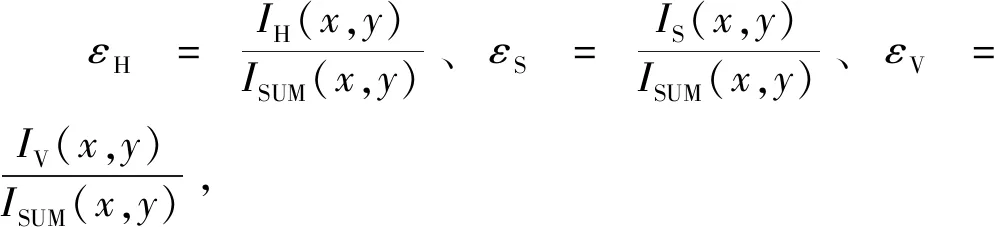
g(x,y)=εHgH(x,y)+εSgS(x,y)+εVgV(x,y)

(3)

通过加权合成的梯度图像，既可以准确定位图像轮廓，又可以最大限度地保留各分量的边界信息。

图2 梯度图像

3.2 形态学梯度重建

分水岭算法直接处理梯度图像时，会因噪声或梯度边缘过厚引起的轮廓定位误差而导致过分割现象，因此，需要对梯度图像进行形态学滤波重建[11-12]。

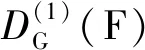
(4)

反复迭代该过程k次至稳定状态，得到F关于G的测地膨胀的形态学重构表达式为：

(5)

测地腐蚀与测地膨胀互为对偶运算，在此不作介绍。本研究算法首先将梯度图g作为掩膜，腐蚀梯度图作为标记，然后基于开操作实现图像重构：

ho={(gΘse)⊕se}∩g

(6)

之后再对开重建图像进行膨胀，并将其补集作为闭重建过程中的标记图像，同时取开重建图像的补集作为模板图像进行重构，得到基于闭操作的重构图像：

hoc={～(ho⊕se)⊕se}∩(～ho)

(7)

由上述可知，形态学重建结果的好坏与结构元素的选取密切相关。结构元素[13]是提取分析图像特征的“信息元探针”，其形状、大小直接影响图像特征量化的结果。一般选择与目标特征轮廓相似、大小相近的结构元形状，以最大程度地减少图像信息的丢失，较好地恢复图像目标的细节边缘。因此，结构元素的选择必须结合图像自身以及实验中的具体情况分析确定[14]。

形态学重建简化了梯度图像，减弱了梯度对于图像边缘方向性的依赖，保留了图像的重要轮廓信息，同时梯度图像中由噪声和非规则细节引起的伪极小值也被剔除，从根源上消除了产生过分割现象的可能。

3.3 形态学标记提取

为了获取感兴趣的目标区域，需要用标记图像对梯度图像进行修正，使图像只在特定的位置产生区域极小值[15]。因此，本研究提出了一种新的获取标记图像的方法，通过将梯度图像区域化来寻找局部区域中的梯度极小值以构成前景标记图像。根据经验，在图像内部的相邻像素间灰度值变化较小，梯度值小，而位于图像边缘的相邻像素间的灰度值变化剧烈，对应的梯度值大。所以，通过像素灰度值的分布情况将图像划分成若干个独立区域，然后对每个区域进行局部极小值梯度标记，即可实现对图像内部像素的充分标记。具体方法为：

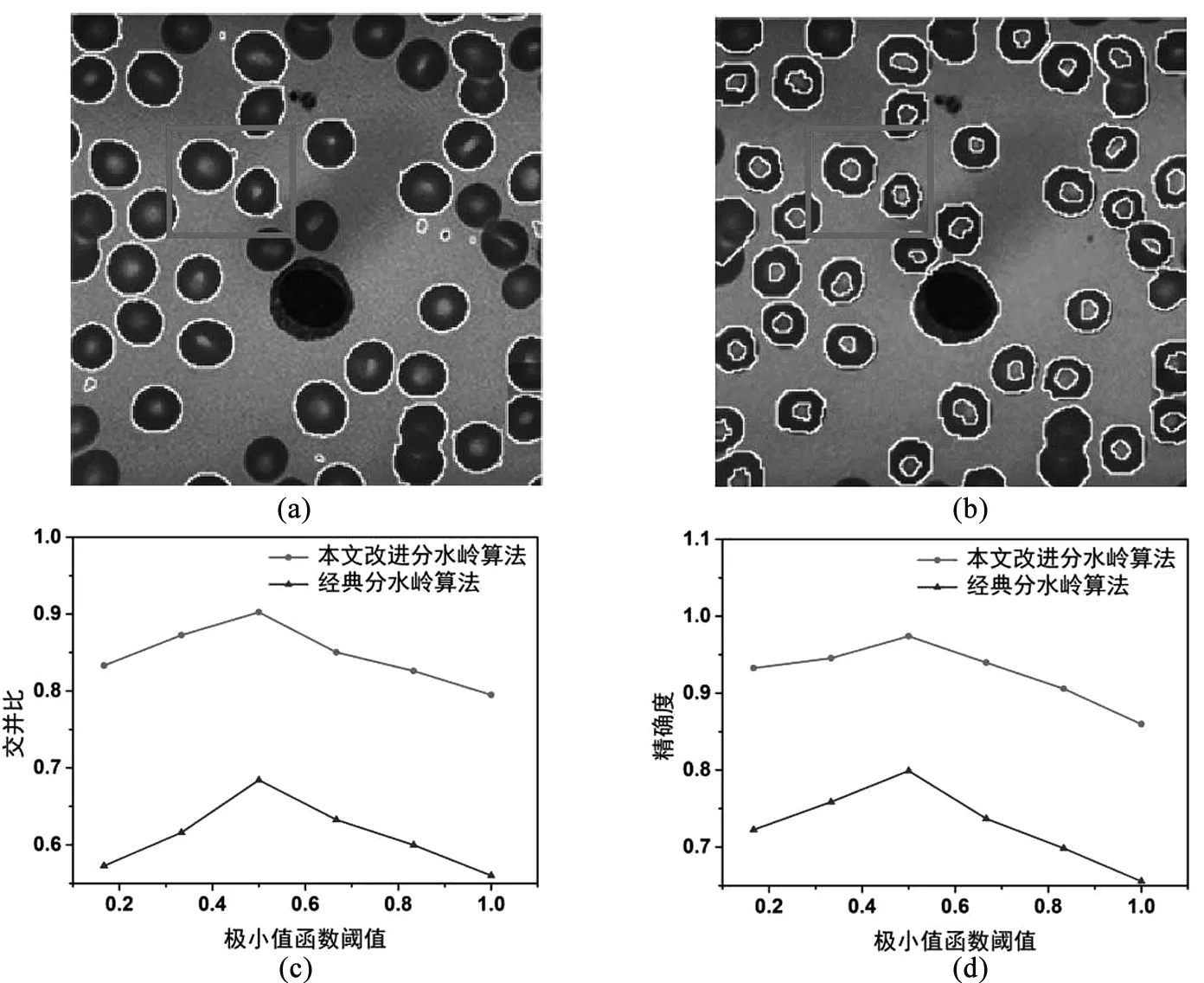
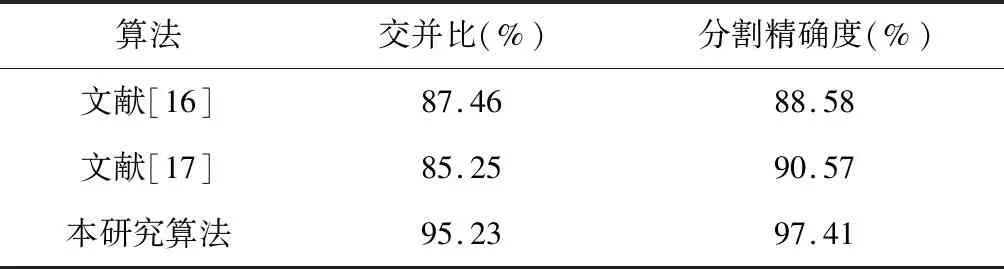
(1)先将灰度图像f平分为m个区域(区域大小视图像尺寸而定，应尽量小)，计算每个区域像素灰度值的方差，然后与图像整体的灰度方差值(定义为阈值)进行比较，当灰度方差大于该阈值，表示该区域包含的主要为边缘像素点；灰度方差小于阈值，则表示包含的多为图像内部像素点，然后将所有小于方差阈值的区域记为M1,M2,...,Mr(r

(2)将灰度图中r个区域的位置关系映射到梯度图像(f→g)，在梯度图像g中统计r个区域内图像梯度等级Xn的分布情况，并将区域内的梯度均值作为标记阈值Xs。

(3)比较M1区域中的各级梯度Xn与阈值Xs1，当XnXs1时不做标记。遍历M1区域中的所有梯度级并找到该区域范围内的所有极小值后，将M1区域标记的局部极小值图记为标号label1。

(4)重复步骤3，对M2～Mr区域内的梯度极小值进行标记，确定r-1个标号区域，最后由r个局部极小值的标号图像构成前景标记图：

fgm={label1+label2+…+labelr}

(8)

通过上述方法，可以将标记点限定在目标区域而避开图像边缘，再利用距离变换“细化”前景标记图，对距离图像做分水岭变化求出背景分割脊线，分割脊线正好将连通的前景标记分隔开，将其作为背景标记图像bgm。

3.4 梯度修正及分水岭分割

利用前景、背景标记图像对梯度进行修改，屏蔽原梯度图像中的极小值而凸显被重新标记的局部极小值，去除伪极小值对梯度图像的影响，使检测到的图像边缘更加准确清晰。本研究对Canny算子检测到的HSV颜色空间加权梯度图进行形态学滤波重建后，利用强制极小值技术结合形态学前景、背景标记对其进行梯度修正，使局部极小值只出现在前景图像中标记的位置。修改后的待分割梯度图像g为：

g=imimposemin(hoc,fgm|bgm)

(9)

将其应用于分水岭变换求出分割结果图f:

f=watershed(g)

(10)

4 实验结果与分析

4.1 细胞图分割结果

为验证Canny算子在本研究算法中的有效性，我们进行了两组对比实验以评价分割结果。实验一为形态学改进的分水岭算法与经典分水岭算法的对比，其分割结果及评价参数见图3。图3(a)、(b)分别为改组对比实验的分割结果。由图3(a)可知，经典分水岭算法只分割出了部分细胞(约为总细胞数的70%)，且分割出的细胞轮廓定位不够准确；利用形态学操作优化后的结果见图3(b)，分割出的红细胞数约占细胞总数的98%，同时，形态学处理可以提取到图像更多的暗部细节特征，得到的分割线边缘光滑，无凸起，定位也更精确。本研究在对细胞图像的分割结果进行分析评价时，选取了交并比(intersection-over-union, IOU)和分割精确度(Precision)两个特征参数进行判断，两个参数值越高，表示分割效果越好，结果见图3(c)、(d)。经计算得出，形态学改进的分水岭算法其IOU值和Precision值比经典分水岭算法分别提高了14.96%和11.95%。

4.2 形态学结构元的影响

结构元素的选取是影响分水岭算法分割结果好坏的重要因素，因此，本研究对结构元素的选取做如下分析：选择三幅目标各不相同的图像进行分析研究，并选取线形、圆盘形、菱形三种形状的结构元素对每一幅图像进行实验，见图5。其中，图5(a)、(b)为结构元尺寸一定时，结构元形状对图像分割的影响。图5(a)中的分割目标为大米颗粒，由图可知，线形、圆盘形、菱形三种结构元的未分割目标数量依次减少，其占总目标数的比率分别为0.355、0.282、0.186，由于线形结构元与图像目标的形态及大小相差较大，在参与运算时不能最大限度地对目标进行提取；而圆盘结构更容易将多余的背景区域覆盖造成过分割现象，因此，选择菱形作为提取大米图像的结构元。图5(b)中的分割目标为红细胞。线形、菱形、圆盘形三条曲线未分割出的红细胞数占总目标数的比率依次为0.389、0.279、0.257，即圆盘形结构元更适于对红细胞图像的分割。由此可知，当结构元大小一致时，越符合图像特征的结构元形状提取到图像信息越完整，且能够最大程度地保留原图像的几何形状。

图3 经典分水岭算法与形态学分水岭算法分割结果对比图

实验二为本研究改进的分水岭算法与经典分水岭算法的对比，二者的分割结果对比见图4。其中，图4(a)结果与图3(a)一致。图4(b)为本研究改进分水岭算法的分割结果，该图中分割出的细胞数约占细胞总数的98%，且分割边缘更贴合细胞的真实状态，能够较好地识别红细胞的具体形态，有助于进一步观测红细胞的大小变化，并为检测红细胞是否产生病变提供依据。利用IOU和Precision两个参数对7分割结果进行分析对比，结果见图5(c)、(d)，显示本研究提出的基于Canny算子提取加权梯度和形态学修正梯度图的改进分水岭算法较经典分水岭算法的IOU值和Precision值分别提高了31.86%和21.88%；与只有形态学优化的分水岭算法相比，其值分别提高了14.69%和8.87%。通过两组对比实验可以得出，本研究的改进分水岭算法分割效果更佳，具有一定的可行性与有效性。

图4 经典分水岭算法与本研究改进算法的分割结果对比图

图5(c)、(d)为结构元尺寸对图像分割影响的结果。图5(c)中结构元尺寸从S1变为S2时，未分割出的大米颗粒数量逐渐减少，占总数量的比率分别为0.19、0.154；当结构元尺寸为S3时，未分割目标数量的比率达到最小值0.141，此时的分割准确度最高；当结构元尺寸继续从S4变为S6时，未分割出的大米颗粒数量重新增多，结构元各尺寸对应的未分割目标比率也分别增大至0.205、0.224、0.257。在图5(d)中，结构元从S1增大到S5的过程中，未分割出的红细胞数量均在逐渐减少，其占总目标数的比率分别为0.497、0.319、0.254、0.249，并在S5的时候达到了最小值0.194；当继续增大结构元为S6时，未分割出的目标比率增大为0.393。因此，由图5(c)、(d)可知，当结构元的尺寸与目标大小相近时，分割效果最好，因为结构元的增大意味着“探针”可携带的图像信息变多，能够更精准地描述图像的结构特征并识别目标。但无限地增大结构元素，将导致图像的一些局部细节被模糊掉，在形态学重建时，能更完整地恢复原图像形貌，从而造成最终的分割结果准确性降低。

4.3 客观评价参数对比

表1给出了本研究改进的分水岭算法与文献[16]、[17]的交并比和精确度性能参数的对比情况。文献[16]的算法中图像受光照情况影响较为明显，对光照不均匀或曝光度高的细胞存在欠分割情况，故分割精确度较低；文献[17]的算法中粘连细胞在边界处的亮度变化较弱，易造成细胞边界检测不全，引起过分割现象。而本研究算法利用图像HSV颜色空间的各分量梯度求加权拟合梯度，避免了原细胞图像信息丢失，同时在形态学重建时修正对梯度图的充分标记，剔除了细胞图像中的伪极小值，使图像信息被充分表达，其分割精确度较文献[16]、[17]分别提高了9.97%、7.55%，获得的细胞边缘更加完整、连续且无过分割现象。

图5 形态学结构元对分割结果的影响

表1 不同算法性能参数比较结果

5 结束语

本研究改进的分水岭算法不同于经典分水岭算法中直接对灰度图像的梯度图进行提取和分割，而是由Canny算子获取图像HSV颜色空间的各个梯度分量后进行加权拟合，保留更多的图像细节，然后对平滑后的拟合梯度图进行区域化，使得待标记的目标像素趋于集中，之后标记局部极小值时只在包含内部像素较多的区域进行，最后利用标记图像对梯度图进行形态学修正并求出分水岭分割结果。实验结果表明，本研究算法与经典分水岭算法相比，其交并比(IOU)参数值提高了31.86%，分割精确度提高了21.88%，对比文献[18]、[19]，本研究算法的分割精确度均有提高，因此，可用于后续细胞图像的识别分类研究。后续研究工作将在已有基础上对算法作进一步的丰富与扩展，以应用于更加复杂的图像处理领域。