基于亚像素位移的显微CT部分体效应抑制研究

王天舒，李静，罗守华

东南大学 生物科学与医学工程学院，江苏 南京 210000

引言

探测器分辨率不足引起的部分体效应[1]（Partial Volume Eff ect，PVE）会导致重建图像物体边缘模糊，减小物体结构和背景信号间的对比度，降低高分辨显微CT的重建图像质量和定量精确性[2]。引入额外信息对重建体素进行上采样是降低PVE效应的有效方法。

目前引入额外信息提高重建分辨率有如下方法。基于重建物体内物质先验信息进行迭代的高分辨重建[3]，但这种方法只适用于由少量均匀材料组成的物体；基于稀疏表示理论和字典学习的高分辨重建方法通过训练一系列低分辨和高分辨图像块提高重建分辨率[4]，但重建图像的质量很大程度上取决于所采用的稀疏域能否通过联合训练低分辨率和高分辨率字典来充分地表示目标图像；基于卷积神经网络的超分辨方法用于高分辨重建[5-6]，但神经网络训练需有大量的数据集，在高分辨显微CT系统中，克服部分体效应的高分辨数据集获取困难。基于亚像素位移信息的高分辨重建[7-9]，这些方法的关键在于如何获取含亚像素位移信息的投影图像。Yan等[10]利用螺旋CT采图特点，得到CT图像Z轴上的亚像素位移图像，进行超分辨重建，提高了螺旋CT的Z轴图像分辨率，进一步的研究使用移动探测器的方式提高x、y轴的分辨率[11]，但该方法仅适用于螺旋CT系统。Liu等[12]使用了临床CT上的飞行焦斑技术，获取低分辨序列数据进行超分辨重建 。Chang等[13]使用了双焦点CT系统，其主要思想是将微焦点源的高分辨率与大功率X射线源的强穿透性相结合 。但以上两种方法对射线源有特殊要求，难以应用于显微CT。

基于透镜耦合的高分辨显微CT[14]，其分辨率可达10 µm至亚微米，能对骨骼、牙齿、生物标本等离体标本进行高分辨的三维成像[15-18]。由上述分析可知，目前基于先验知识、稀疏表示和卷积神经网络的超分辨率重建方法应用于高分辨显微CT系统有很多限制。同时，基于光学透镜耦合的高分辨显微CT，具有高精度驱动单元，高质量的X射线源和透镜耦合的探测器系统，很难通过移动探测器或X射线焦斑来获取具有亚像素信息的投影图像。

结合高分辨显微CT系统的结构特点，本文提出一种基于纳米载物台抖动的高分辨显微CT重建算法（De-PVE FDK，DP-FDK），该方法使用重复精度高的纳米载物台控制待测物体的位置，在每个投影角度得到多张具有亚像素位移信息的投影图像；通过Insight Segmentation and Registration Toolkit（ITK）框架设计了高精度位移向量测量算法[19]，建立纳米载物台位移与投影图亚像素位移之间的对应关系；最后利用基于位移矩阵的FDK算法，上采样重建网格将投影图的亚像素位移信息与FDK重建反投影过程相结合。

1 方法

基于DP-FDK的具体实现过程包括以下三个部分：基于纳米载物台抖动的扫描方案设计，投影图亚像素位移测量算法设计与结合位移矩阵的FDK重建算法设计。

1.1 基于纳米载物台抖动的扫描方案

结合纳米载物台抖动的具体扫描方案如图1所示。CT投影图拍摄首先确定n个定点亚像素位置，每一个角度都需要将待测物体利用纳米载物台移动到n个定点之后拍摄n张具有亚像素位移的投影图像。位移矩阵参数需提前测量并写入配置文件，最终通过结合位移矩阵的FDK重建算法获得高分辨重建图像。

图1 基于纳米载物台抖动的扫描方案

1.2 位移矩阵测量

方案采用纳米级精度的三维平移载物台用于获取含亚像素位移的投影图像，该纳米载物台量程范围为80 µm/轴，分辨率为7 nm，重复定位精度为0.05% F.S.，线性度为0.15% F.S.。

我们假设纳米载物台的实际移动轴XYZ为坐标系A，重建坐标系为坐标系B。由于纳米载物台能够在x、y、z三个方向上对待测物体进行纳米级精确位移且不旋转物体，则坐标系A中实际位移向量（dxreal,dyreal,dzreal）与坐标系B中对应的像素位移向量（dx,dy,dz）之间关系表示如公式(1)所示。

其中F(.)为测量两组图像位移向量的亚像素配准算法，它的输出结果是重建图像沿着x、y、z轴的移动大小。本文中三维图像的亚像素配准基于ITK平台实现。由于纳米载物台进行亚像素位移过程中待拍摄物体不存在非刚性变换以及旋转，因此配准只需要考虑三维刚性平移变换。

获得方向向量之后，纳米载物台移动任意位置都能够在重建坐标系里面获得相对应的位移矩阵M。实际实验中我们使用多组图像来平均误差。在不改变高分辨显微CT系统的情况下，这组参数可以一直使用[20-21]。

1.3 结合位移矩阵的重建算法

我们设计了一种结合位移矩阵的FDK重建算法来重建纳米载物台不同抖动位置的多组投影图。锥束重建坐标系如图2所示，以射线源到探测器平面的垂线与探测器平面的交点为坐标原点O，射线源与坐标原点O的连线为y轴，旋转轴为z轴。s为射线源的位置，Q为重建点，p为Q的投影点，令s到p的直线为投影线。为投影线与y轴负方向之间的夹角，焦距D为s到O的距离。基于位移矩阵的FDK算法主要有四步：

图2 锥束重建坐标系

第一步和第二步为传统FDK算法中的投影数据预处理和一维斜坡滤波过程，如式(5)和式(6)：

第三步是坐标变换。假设被扫描物体的初始坐标为(x,y,z)T，Mβ为旋转角度为β时、位移向量为(dx,dy,dz)时的仿射矩阵，位移后的坐标(xMβ,yMβ,zMβ)T可由式(7)得出：

第四步为单个角度下的反投影过程，将这个操作定义为B，见公式(8)：

最终重建的CT值是各角度下通过该体素的所有角度投影的贡献之和，公式(9)中N为投影角度数，且，

2 结果和讨论

本文采用一组仿真数据与一组竹签真实数据验证算法的有效性。实验中所用数据由实验室自研的透镜式耦合高分辨CT拍摄获得。相应的扫描参数如表1所示。

表1 重建参数

2.1 仿真数据结果

仿真模体的结构示意图和断层截面示意图如图3所示。仿真过程中所加的模糊矩阵为标准差为1的高斯模糊，并添加了泊松噪声以及标准差为0.000001的高斯噪声，并且在仿真投影图制作了坏点来仿真环状伪影。仿真实验探测器像素大小为仿真数据像素大小的10倍，正投影过程由The Astra Toolbox模块获得。

图3 模体示意图

仿真实验中待测物体在重建坐标系中的实际位移向量已知。一共进行了4组仿真实验，分别为1个位置、4个位置、9个位置和16个位置。位移设置，见表2。

表2 仿真实验位移位置表

根据数据量的大小将四组重建的放大倍数分别设置为1、1.45、1.6、2.5。从重建结果可以看出4个位置相对于1个位置重建出来的图像细节恢复明显，位置数目继续增加后对重建结果有一定加强但是效果轻微，表明亚像素信息对分辨率的提高存在上限（图4）。此外，纳米台抖动的扫描方式避免同一像元的误差在重建过程中重复作用于同一个圆周，有抑制环状伪影的作用[20-21]。图4a中黄色箭头处可以明显看到环状伪影，图4b～d中环状伪影得到去除，表明该算法对环状伪影也有一定抑制作用。

图5分别计算了四组重建图像结果与原始仿真图像之间的结构相似度（Structural Similarity，SSIM），可以看出图像的SSIM值随着移动位置数目的增加而提高，定量说明了基于投影图亚像素位移的DP-FDK算法有助于图像分辨率的恢复。

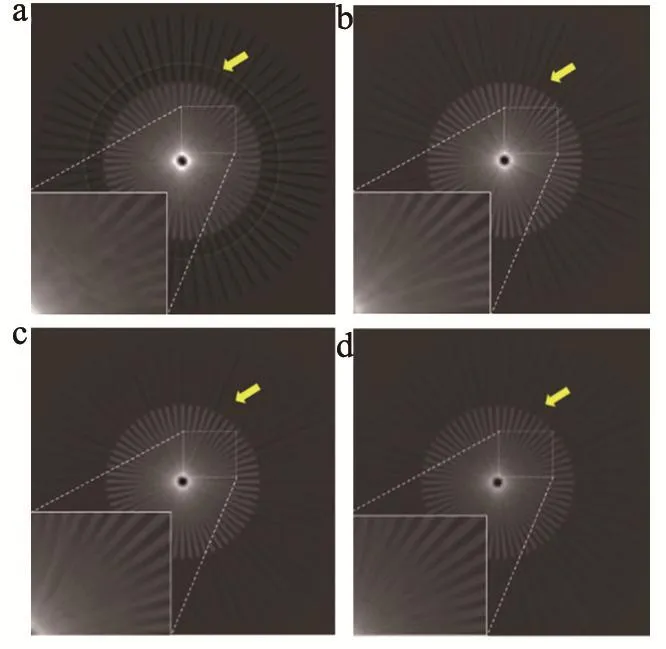
图4 仿真数据重建结果

图5 SSIM随位移位置变化曲线图

2.2 真实数据结果

实际试验中一共移动了4个位置，DP-FDK重建上采样倍数为2，具体位移和位移向量，见表3。从竹签的FDK和DP-FDK重建图像结果可以了解到DP-FDK对环状伪影有部分抑制作用，且从局部放大图像得出DP-FDK结果比FDK结果增加了更多的图像细节，物体结构边缘更清晰（图6）。由于DP-FDK重建网格经过两倍上采样，我们通过双线性插值的方法将FDK重建图扩大两倍，之后做归一化灰度曲线图（图7）。由灰度曲线可以看出DP-FDK的边缘比普通FDK重建更为锐利，物体结构与背景间的对比度更高。由此得出DP-FDK重建比普通FDK重建一定程度上提高了分辨率。

表3 纳米台位移参数及位移向量

图6 竹签重建结果

图7 FDK和DP-FDK重建结果中蓝色和红色虚部分的归一化灰度值

3 结论

本文提出了一种基于投影图亚像素位移的DP-FDK，应用于高分辨显微CT重建。首先利用重复精度高的纳米载物台控制待测物体的位置，得到多组含有亚像素信息的投影图像；同时基于ITK框架设计了高精度位移向量测量算法，实现直接利用纳米载物台移动坐标计算位移矩阵，获取亚像素位移信息；最后设计基于位移矩阵的FDK重建算法，实现上采样重建网格以降低PVE效应，同时能够打破环状伪影的形成机制。由仿真实验以及实际实验结果可知，本文提出的DP-FDK算法，能够提高图像的重建分辨率、重建速度快，对于具有复杂成像系统的透镜耦合式高分辨CT非常适用。