ADC 测试中同源时钟分析与解决方案
钱宏文, 刘继祥, 吴翼虎, 饶 飞
(中科芯集成电路有限公司, 江苏 无锡 214072)
1 引言
随着科学技术的快速发展,低功耗、高度集成、微型化成为未来微电子技术的发展趋势。 模数转换器(ADC)作为集成电路技术的重要组成部分,对ADC 性能参数的精确测试是确保其可靠性应用的前提。 在对ADC 性能参数进行测试时发现, 应用同源时钟为ADC 芯片提供时钟源和信号源时,静态指标测试结果严重超差。 为了分析该问题,应用MATLAB 对该场景进行仿真测试,通过深度分析,最终解决同源时钟静态指标测试问题。
2 ADC 测试简介
ADC 静态参数主要有差分非线性(DNL)、积分非线性(INL)[1]。静态参数反映了ADC 的自身性能,当前,静态参数的主要测试方法包括直方图测试和基于动态参数估算静态参数两种方法。 直方图方法包括斜坡输入和正弦输入两种情况。 随着ADC 精度的不断提高, 要求斜坡发生器输出的非线性度也要跟着提高,在增加测试成本的同时对高精度信号发生器会产生过度依赖, 在特殊时期就有可能受到国外厂商的掣肘。 本文通过正弦信号输入,利用直方图进行统计,完成静态指标测试, 相对于斜坡直方图方法节省时间,在测试装置不变的情况下, 可以同时满足动态参数、静态参数的测试。
ADC 数据采集中应注意以下几点:
1)输入信号的频率与采样频率[2]之间必须满足奈奎斯特采样定理,即fs≫2fin(max)。
2) 样本数(需要理论依据)输入周期信号频率与采样频率成互质关系, 以符合统计的随机分布性;在同源时钟时,应尽可能提升输入信号频率的精度以提高采样的随机性,避免漏码发生,这就需要对输入信号频率与采样信号进行约束,使采集到的码值尽可能覆盖ADC 芯片输出码值, 即需选择特定频率的输入信号与采样频率,从而使得采集到的采样数据能在记录长度内转换的代码尽可能多。 这是通过输入信号频率与采样频率之间的一种基本关系实现的,如式(1)所示。

fin为输入信号频率,fs为采样频率,Ncycles为完整采样的周期数,Nsamples为采样总点数。
一般为方便处理,Nsamples取2 的整数次幂,Ncycles取与Nsamples互质的整数。 由于输入正弦信号的时间与幅度关系是不均匀分布的,在统计码密度时就会发现峰峰值附近处的采样点数远多于靠近幅度为0 的点;因此正弦-直方图的缺点就是需要采集较大的样本数[3]用以消除正弦波电压分布的不均匀性。
对于一个理想的待测ADC 来说, 其码值的统计直方图应该呈浴盆状分布,具体如图1 所示。

图1 理想码密度统计图
ADC 测试所需样本数取决于ADC 分辨率N、DNL 误差精度以及测试结果置信水平[4],对于待测的16 位两通道AD****,其DNL 典型值为0.7 LSB,置信水平为95%和99%,其样本数NR可根据式(2)、(3)得出:
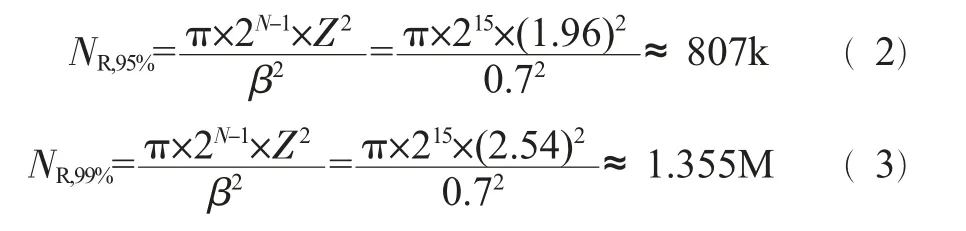
Z 为置信度,β 为测试精度。
3 测试平台硬件设计
3.1 硬件架构
硬件系统是采用SOC+FPGA[5]架构进行设计的,输入信号经过滤波器后与时钟信号一起接入硬件系统,其中输入信号与时钟是由一台信号源产生,硬件系统进行数据采集后通过以太网传输至上位机,上位机软件完成数据接收、算法分析、测试指标结果显示,如图2 所示。
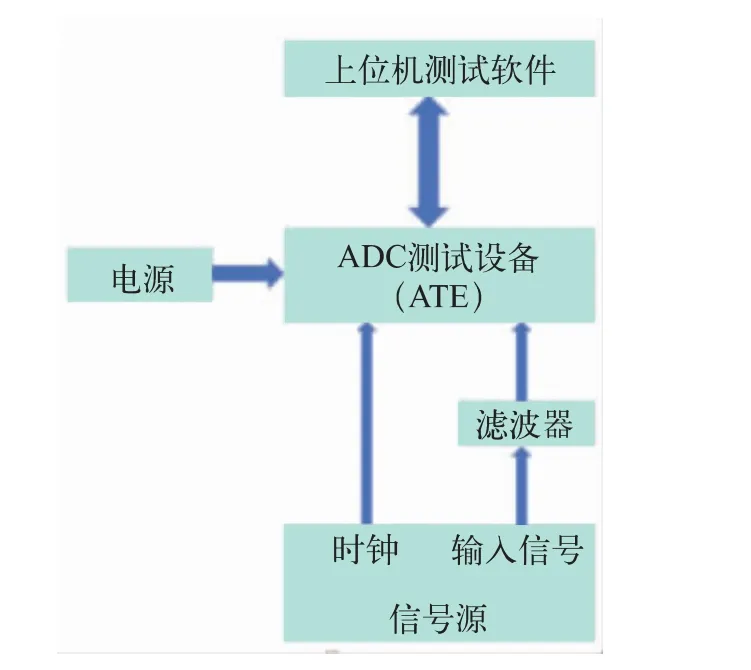
图2 系统流程图
3.2 软件架构
上位机软件采用LabVIEW+MATLAB[6]架构,与ZYNQ7020 千兆网口进行通信,通过更新数据库、配置文件、Matlab 算法(com 组件)、FPGA 在线加载等功能模块,以此实现不同型号芯片的快算测试。
3.3 应用
以16 位两通道AD****为例,采样频率和输入信号由一台信号源两个输出端口提供,当采样频率输入125 MHz、 输入信号10.1 MHz、 单通道采样点数4M时,得到INL、DNL 指标测试结果严重超差;若采样频率和输入信号分别由两台信号源提供,静态指标测试合格。 针对这一现象,我们怀疑输入信号分辨率过低,时钟信号在采样过程中无法随机进行采样,导致码值采集遗漏而造成静态指标测试结果严重超差。 以下将通过MATLAB 进行仿真测试。首先MATLAB 需要生成125 MHz 的时钟,采样10.1 MHz 的正弦波,并进行幅值-码值转换(模拟真实ADC 采集场景),其次通过统计绘制出直方图,最后对0~65535(216)进行统计,码值统计数为0 则代表此处丢码。 MATLAB 程序如图3 所示。
当输入信号10.1 MHz 时,丢码率过高,不具备可观察性; 故将输入信号频率更改为10.123 MHz 时,通过MATLAB 仿真,如图4 所示。
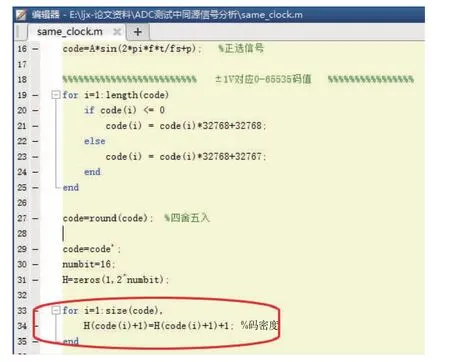
图3 MATLAB 程序
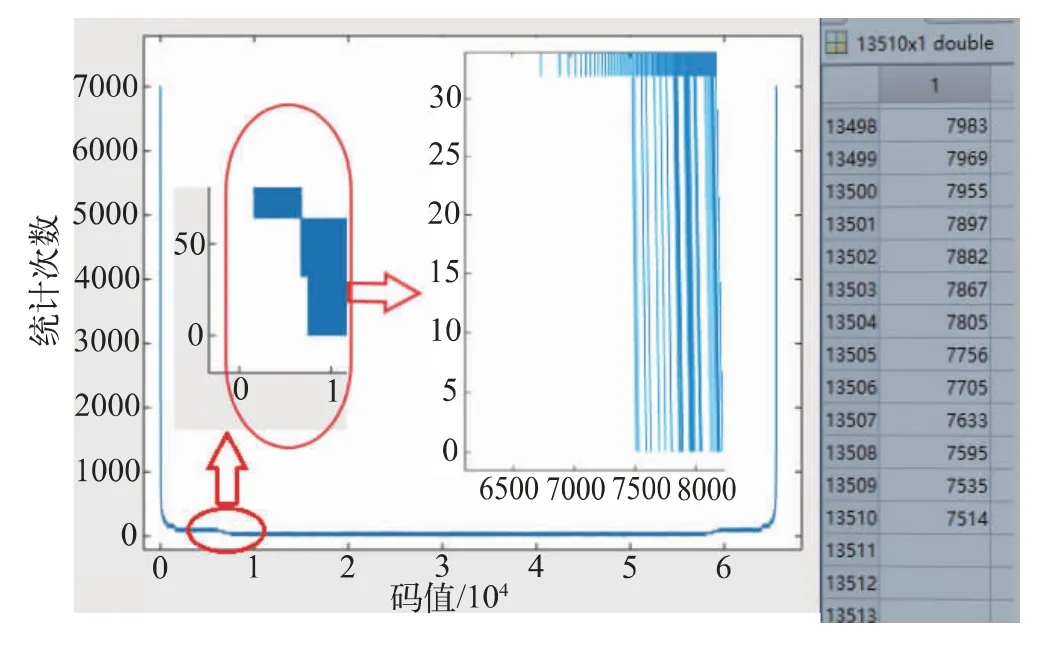
图4 码密度统计图
统计丢码数13510,最小丢码值7514。按照同源时钟情况进行仿真,首先将已知条件代入式(1)中:
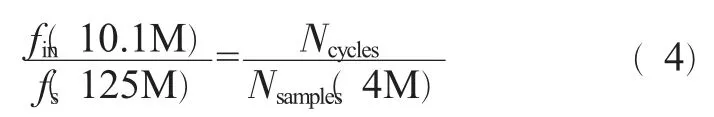
得到Ncycles=336666.7,取整336667,代入上式得:

得到fin=10100031 Hz。
将输入信号频率更改为10100031 Hz 时, 单通道采样点数4M,其仿真结果如图5 所示。
从图5 可知, 无丢码现象发生且每个码值最小采样次数均大于30,同源时钟下,输入信号分辨率与丢码率之间存在直接影响; 输入信号分辨率足够高,丢码率越低。
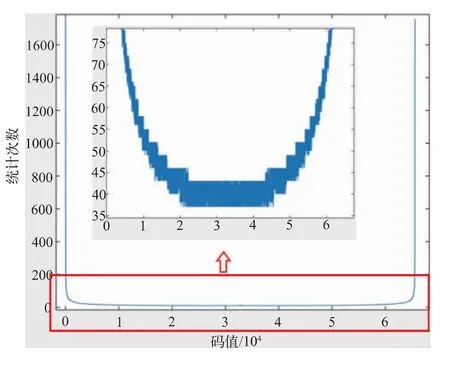
图5 仿真结果
保持输入信号频率10100031 Hz、 将样本数设置为807k(置信水平95%),无丢码现象且每个码值最小采样次数均大于4; 保持输入信号频率10100031 Hz、将样本数设置为1.355M(置信水平99%),无丢码现象且每个码值最小采样次数均大于10。
一般采用码密度直方图进行ADC 静态参数测试时,若输入为正弦信号,每个码采样数应不少于30 个,故单通道采样点数4M。
由此可见,在同源时钟下,码密度采集与输入信号分辨率、采样点数密切相关。
4 测试结果
再次以16 位两通道AD****为例,采样频率和输入信号由一台信号源两个输出端口提供,当采样频率输入125 MHz、输入信号101000031 Hz、单通道采样点数4M 时, 得到INL、DNL 指标测试结果如图6 所示。
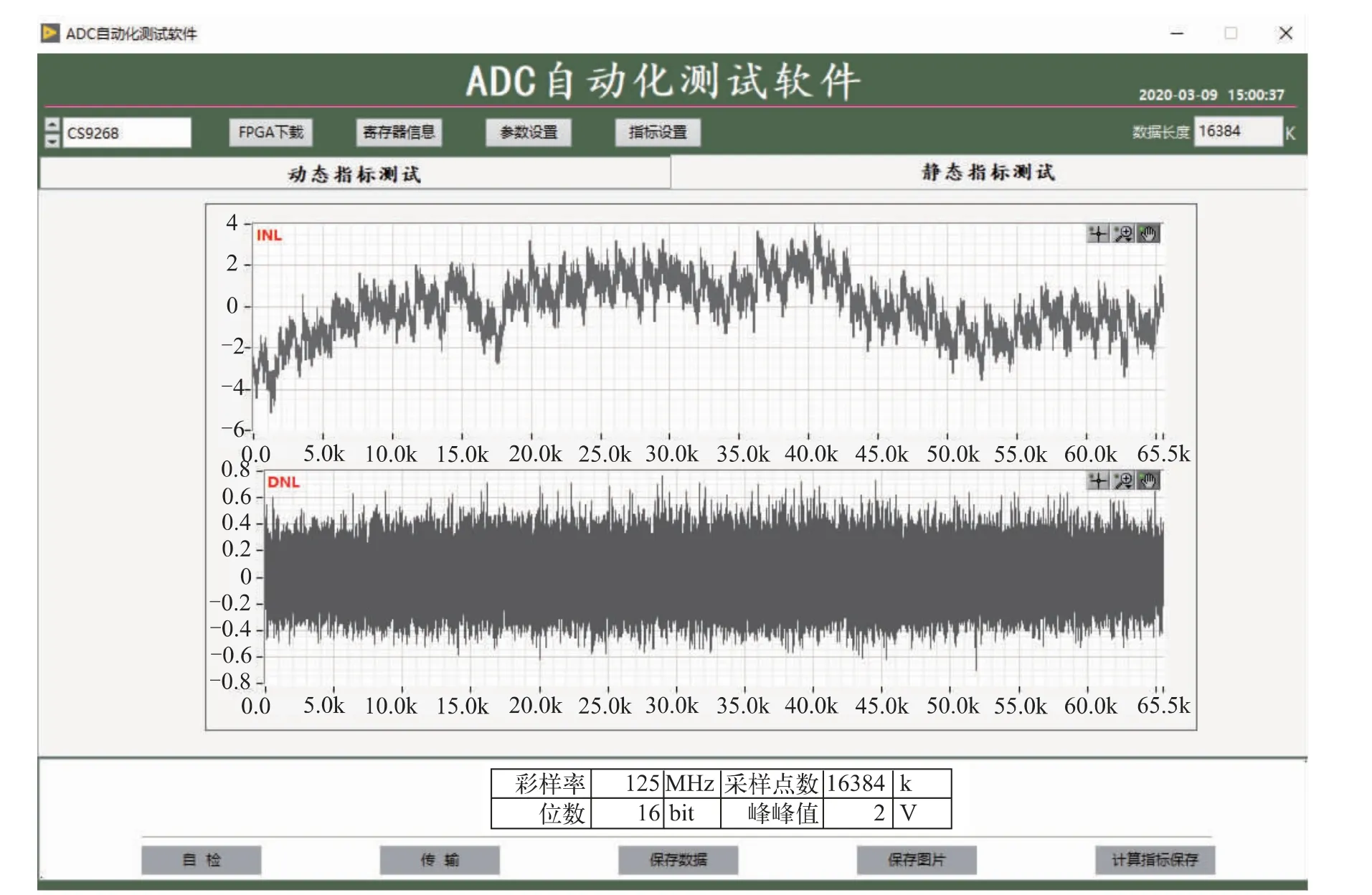
图6 静态参数
实测指标与数据手册对比如表1 所示。

表1 测试结果与AD**** 数据表对比
5 结论
通过输入信号频率与采样频率之间的基本关系计算出输入信号频率,可以有效解决同源时钟下静态指标异常的问题;通过置信水平公式可以得到最优样本数据个数,能够提高采样效率,为后期批量测试节省时间。 本文针对同源时钟下静态指标异常问题,通过理论分析、仿真设计、实物验证,为后期ADC 测试中同源输出提供了很好的解决方案,具有一定的启发价值。
——紫 苏

