实代数曲线的孤立零点

2021-01-26 12:10徐嘉

西南民族大学学报（自然科学版） 2020年5期

关键词：实根折线正数

徐嘉

(西南民族大学数学学院，四川成都 610041)

实系数多项式f(x，y)∈R[x，y]的实零点是指集合VR(f)

VR(f)传统上称为实代数曲线.虽然VR(f)可能是空集(例如而不是真正的曲线(一维几何对象).f(x，y)的实零点又分为两类，奇异点和非奇异点.如果点P∈R2满足

则称为奇异的，否则称为非奇异的(或正则的).而奇异点中有一类点具有特殊的重要性，那就是孤立零点.一个点P∈R2被称为代数曲线VR(f)的孤立零点如果它满足以下两个条件:

1)f(P)=0

2)存在充分小的正数ε使得

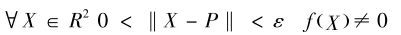
条件2直观的说法是:在一个中心为P半径充分小的圆内，除了点P以外f(x，y)没有其它的实零点.等价地说，f(x，y)在P的附近有恒定的符号.因此孤立零点又可分为两种类型，极小型和极大型，分别对应着条件在P的附近f(X)＞0和f(X)＜0.容易看出P是曲线VR(f)的极小型孤立零点⇔P是曲线VR(-f)的极大型孤立零点.

因此，我们研究极小型孤立零点就足够了.

通过坐标的平移，我们总可以假定P是原点(0，0)，而不会改变问题的实质.当然，一般情况下点P的坐标可能是较为复杂的实代数数，对于代数数的处理已经有较为成熟的方法可参考文献[1-2].我们将集中精力讨论原点的孤立性.本文中研究的主要问题是:

给定多项式f∈R[x，y]，判断原点是否代数曲线VR(f)的孤立零点?

实代数曲线的孤立零点有基本的重要性，它涉及许多其它的数学问题.如曲线在奇异点附近的拓扑结构问题，例如代数曲线VR(f)，f=(x-y)20+x40-x10y20+x28在原点附近是否有实分枝?这类问题在计算机辅助几何设计中常常会遇到.另一类问题是函数的极值点问题.例如对多项式函数

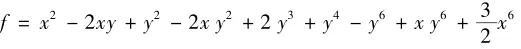
问:原点是否f的极值点?如果是，是极大值点，还是极小值点?否则，是鞍点吗?判断极大极小点问题是最优化理论中的基本问题，常常使用熟知的海赛(Hessen)矩阵方法[3].但是当海赛矩阵是奇异矩阵时该方法失效.

人们对实代数曲线的研究已经有相当长的历史.对于孤立零点的研究也积累了大量的资料和方法.首先，一种较为平凡的方法是实量词消去方法.也就是将问题归结为如下的量词消去问题，给定实量词公式

求等价的无量词公式.标准的量词消去工具，如塔斯基方法(Tarski)[4]，著名的柱形代数分解方法(CAD)[5-6]，都可以被使用来解决孤立零点的问题.2019年文献[7]新近建立的一种方法是将问题归结为一个最优化问题，然后使用数学规划的策略解决问题.这几种类型方法的复杂性对多项式的次数有较大的依赖性.在针对下面这类多项式时，有明显的不足.考虑多项式

容易发现原点(0，0)是这个多项式的孤立零点，它与具体的多项式g(x，y)无关，仅仅只需要g(x，y)的次数大于4就足够了，也就是说它可以是100 000次，然而并不影响原点的孤立性.在本文中我们将要建立一个方法，它充分利用了上面观察到的特点.

本文以下部分的内容被安排为三节，第二节是预备知识，主要复习关于牛顿(I.Newton)多边形和牛顿变换以及单变量多项的实根隔离等基本内容，它们是证明主要结果和建立算法的工具.第三节是主要结果及其证明.最后一节是算法的描述以及运算实例.

1 预备知识

首先，我们需要复习一些关于代数曲线的基本知识，可参考文献[8-9].

1.1 牛顿折线.

令

在实平面R2上描出满足ai，j≠0的点(i，j).我们获得集合

Δ(f)称为f的牛顿图(Newton diagram).牛顿图Δ(f)的凸包是一个凸多边形，它的下边界被称为牛顿折线，记为N(f).牛顿折线另一个严格的定义为:凸集的紧面.其中Conv(S)表示集合的凸包，R+是非负实数集合.

多项式

的牛顿图和牛顿折线见图1.牛顿折线N(f)的一条边T对应了多项式f的一个子多项式，我们记为fT

对本文中，主要被使用的是N(f)最陡的那条边.

注意到有一些平凡的情况会出现.如果N(f)仅仅是一个点时，则必有x|f或y|f，也就是有f(0，y)=0或f(x，0)=0，都表明(0，0)不是曲线VR(f)的孤立零点.

图1 多项式的牛顿图与牛顿折线Fig.1 Newtondiagram and Newton polyline of a polynomial

1.2 拟齐次多项式

多项式g∈R[x，y]被称为拟齐次的，如果存在正整数w1，w2，μ满足

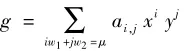
w1，w2称为权.

容易验证任意多项式的牛顿折线的一条边T对应的子多项式fT都是拟齐次的.为了让μ尽可能的小，我们假设w1，w2是互素的，并称这时的μ为g的拟次数.

1.3 牛顿变换

实系数多项式f∈R[x，y]满足f无平方因子，f(0，0)=0，且x f，y f.于是f(0，y)≠0，设d是f(0，y)的最低次数，也记为tdeg(f，y)，则(0，d)是N(f)的一个顶点.我们假定T是牛顿折线N(f)包含(0，d)的那条边.令z是fT(1，y)或fT(-1，y)的一个根，再设

其中w1，w2是fT的权，μ为fT的拟次数.

引理1是多项式.

证明：与通常关于Newton-Puiseux算法中的证明是一样的.可参考文献[8-9].

我们把

称为牛顿变换.

讨论:在经典的文献(如[8-9])中的牛顿变换，只考虑fT(1，y)=0的复根，这对讨论复代数曲线是足够的.但是如果要讨论实代数曲线在实空间的情况，则fT(1，y)的信息是不够的，还需要考虑fT(-1，y)=0的实根.一个简单的例子如下

其牛顿折线N(f)只有一条边，它就是连接(3，0)和(0，2)的线段，fT=x3+y2.此时fT(1，y)=1+y2无实根，这样就得不到关于f在原点附近实分枝的信息.事实上f在原点附近有一个实分枝，对应的Newton-Puiseux展开为

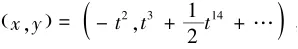
为了得到实代数曲线实分枝的信息，解决问题的思路有两个，一是考虑所谓Rational Puiseux展开[10]，另一个就是同时考虑fT(1，y)和fT(-1，y)的实根.本文的方法属于后者.

1.4 单变量多项式的实根隔离算法

实系数多项式的实根隔离就是求一列互不相交的区间，使其包含该多项式的所有实根，而且其中的每一个区间恰含有一个根.从某种意义上，完成实根隔离就代表求出了多项式的所有实根，我们可以用某个区间来指代那个区间上的代数数并进行各种运算.

实根隔离算法是实代数的基本算法之一.有大量的参考文献[11-13]和基于不同原理的算法.本文中，我们仅仅指出实根隔离算法的基本应用，就是计算给定多项式相异实根的个数，以及判断一个实根是奇数重根还是偶数重根.一个实例如下

例1.考虑多项式

使用实根隔离算法，例如运行数学软件Maple中的命令realroot，我们能够获得三个区间

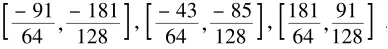
也就是说h(x)有三个不同的实根.计算区间端点的符号可知，位于区间中的实根是偶数重根，因为区间端点的符号相同.而位于区中的根是奇数重根，因为区间端点的符号不同.从下面的分解式可以验证这些断言都是正确的

一般情况也是如此.在下文算法IsolatedZero中需要使用实根隔离算法.

2 主要结果

在叙述我们的主要结果之前先证明几个引理.

引理2：设f∈R[x，y]是非常数的拟齐次多项式.则下面三个条件是等价的.

1)(0，0)是曲线VR(f)的极小型孤立零点；

2)∀y∈Rf(±1，y)＞0；

3)多项式f(±1，y)无实根且f(1，0)＞0.

证明：2与3的等价性是明显的.下面主要证明1与2之间的等价性.f是拟齐次的，记它的权为w1，w2，拟次数为μ.则f(xw1，yw2)，

是次数为μ的齐次多项式.于是有恒等式

1⇒2.如果(0，0)是曲线VR(f)的孤立零点，则由定义不妨设正数ε满足

对任意给定的点(a，b)∈R2/{(0，0)}，考虑曲线又

所以当t充分小时，于是得到:存在正数t使

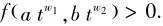
从(1)立刻得到f(a，b)＞0.由于(a，b)是任意的，取(a，b)=(±1，y)，即得

2⇒1.反过来，如果

由于f(±1，y)是只含有y的多项式，所以最大次数是偶数，系数是正数.于是可以推出

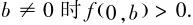
假设a≠0，利用等式(1)，有

其中±1由a的符号确定，保持一致.于是我们证明了，对任意(a，b)≠(0，0)，都有

由定义，(0，0)是曲线VR(f)的极小型孤立零点.

引理3：实系数多项式f∈R[x，y]满足f(0，0)=0.如果存在牛顿折线的一条边T使得∀(x，y)∈R2/{(0，0)}fT(x，y)＞0(或＜0)，则f的牛顿折线只含有一条边T.

证明：注意到如果∀(x，y)∈R2/{(0，0)}fT(x，y)＞0，则fT(x，y)不能被x或y整除.也就是fT(x，y)必须同时满足fT(0，y)，fT(x，0)都不恒为0，记它们的最低次数分别为s，t(s≥1，t≥1).因为fT是拟齐次的，它的所有的单项xi yj对应的点(i，j)都满足线性关系

点(s，0)和(0，t)也在这条线上，所以线段T满足

可见T是凸包的一维紧面.所以f的牛顿折线只含有一条边，就是T.

引理4：(广义平均值不等式)[14]x，y是正实数，a，b，c，d是实数.存在常数λ，0≤λ≤1，使得

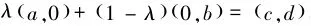
则有如下不等式成立

引理5：实系数多项式f∈R[x，y]满足f(0，0)=0.如果存在牛顿折线的一条边T使得多项式fT(±1，y)无实根且fT(1，0)＞0，则(0，0)是VR(f)的极小型孤立零点.

证明：因为fT是拟齐次的，从引理2的证明，容易看出

由引理3可知f的牛顿折线只含有一条边T.可以将多项式f表示为w1，w2是fT的权，μ是拟次数.因为公式(2)，可知两个单项

注意到对任意单项式xi yj，iw1+j w2＞μ，存在正实数使得是根据引理4，知存在正常数对任意正实数x，y，满足不等式

其中N是求和号中单项式的个数.

于是有

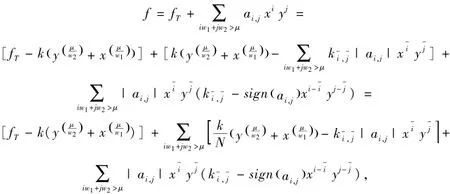
sign(ai，j)是符号函数，即

由不等式(3)有

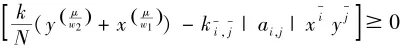
当x，y都充分小时，有

所以当x，y都是正数且时

完全类似，我们能够证明，当x，y都是正数且时

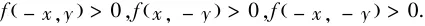
也就是证明了(0，0)是f的极小型孤立零点.

定理1：实系数多项式f∈R[x，y]满足f无平方因子，f(0，0)=0，且x f，y f.T是N(f)中最陡的那条边.(0，0)是曲线VR(f)的极小型孤立零点当且仅当下面两个条件之一成立

1)fT(±1，y)没有实根且fT(1，0)＞0；

2)fT(±1，y)仅有偶数重实根且fT(1，0)＞0，且对fT(±1，y)=0的任意实根γ，(0，0)是曲线的极小型孤立零点，其中由第二节的(*)式定义.

证明：必要性.假设(0，0)是曲线VR(f)的极小型孤立零点，如果fT(±1，y)没有实根且fT(1，y)＞0，则结果显然.如果fT(±1，y)有实根，先来证明fT(±1，y)不能有奇数重实根.反证法，假设fT(±1，y)有奇数重实根，不失一般性，设y0是fT( 1，y0)=0的奇数重实根(y0是fT(-1，y0)=0的奇数重实根的情况完全类似讨论)，则存在一个小区间[a，b]，满足y0∈[a，b]，且fT(1，a)fT(1，b)＜0.令x=tw1，y=tw2根据表达式

有

其中g(t)是一个多项式.当t＞0并趋于0时，的符号与tμfT(1，a)的符号相同.同理，当t＞0并趋于0时的符号与tμfT(1，b)的符号相同，但是fT(1，a)fT(1，b)＜0，也就是说f在原点附近任意小的邻域都可取到正值和负值，所以(0，0)不是曲线VR(f)的孤立零点.矛盾.

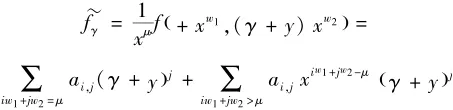
于是当x=0时

当x≠0时，但

于是对一个给定的正数ε存在正数ε2，使得当时

也就是说当(x，y)充分接近原点时，也充分接近原点.根据孤立零点的定义，对充分小的ε3我们有

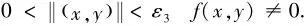
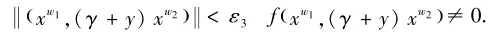
所以

取δ=min{ε1，ε3}，获得

充分性.

如果fT(±1，y)没有实根且fT(1，0)＞0，由引理5，(0，0)是VR(f)的极小型孤立零点.如果fT(±1，y)每一个实根都是偶数重根，由fT(1，0)＞0则有fT(±1，y)≥0.

记

于是Br被分解到了三个部分

条件fT(1，0)＞0推知fT(±1，y)的最低次数d＞0，于是点(0，d)∈T.单项a0，d yd的系数a0，d＞0.因此，V+(f)≠φ.假设(0，0)不是VR(f)的极小型孤立零点，也就是说，存在正数ε当r＜ε时，VR(f)∩Br≠φ.根据曲线挑选引理[15]，我们能够找到实解析函数φ(t)满足φ(0)=0，f(t，φ(t))≡0(t∈(0，ε)).

另一方面，根据代数曲线的基本理论[8-9]，每一个实解析函数φ(t)都可以通过Newton-Puiseux展开来得到，因此φ(t)可以写为的高阶项

其中γ是fT(±1，y)=0的实根.于是