基于自适应DBSCAN的雷达目标跟踪算法

张 巧， 杨红雨,2， 刘 洪,2， 刘 宇,2， 闫 震

(1.四川大学视觉合成图形图像技术重点学科实验室， 成都610065; 2.四川大学计算机学院， 成都610065)

1 引 言

三坐标航管一次雷达回波信号经过雷达信号处理单元后形成雷达点迹数据，但是对于民航等大型目标而言，目标本身尺寸较大，可以跨越多个距离及方位单元，在雷达信号处理之后同一目标仍会产生多个点迹信息.并且对于杂波环境下，由于各种杂波出现的不规则性[1]，特别是雷达在受到地杂波或海杂波影响的区域，每个周期都可能出现大量的点迹报告，给数据处理系统造成极大的压力，严重影响雷达目标跟踪效率[2].

国内外对该问题所提出的解决方案主要在雷达信号处理方面和进行航迹跟踪时算法改进方面.

在雷达信号处理方面，主要是CFAR算法的研究及改进.CFAR检测算法分成两类：瑞利背景下的CFAR算法和非瑞利背景下的CFAR算法.

瑞利背景下的CFAR算法有4类，第一类是均值类(ML) CFAR算法，其中最经典的是单元平均算法(CA) CFAR算法[3].为了减小杂波边缘的虚警，提出单元平均放大(GO) CFAR[4]算法；第二类是有序统计类恒虚警算法，最经典的是OS-CFAR算法[5]及剔除平均(TM) CFAR算法[6-7]；第三类是自适应CFAR算法，其中包括变化指数(VI)CFAR算法[8]及非均匀杂波估计(HCE)CFAR算法[9]；第四类是杂波图CFAR算法[10].

非瑞利背景下的CFAR算法包括Log-tCFAR算法[11-12]等.

张欣[13]提出一种基于对数杂波图的自适应恒虚警检测算法，在复杂杂波背景环境下提高雷达系统的检测性能，有效减少虚假航迹数.

进行航迹跟踪时所用算法的改进方面，主要是对卡尔曼滤波算法的改进.Bar-Shalom等[14]提出扩展卡尔曼(EKF)滤波算法.文献[15]提出无迹卡尔曼滤波，在一定程度上提高了滤波精度.针对高斯分布的非线性滤波问题，积分卡尔曼滤波和容积卡尔曼滤波[16]被提出.

随着人工智能在工程上的大量运用，基于神经网络的卡尔曼滤波被提出.张宇行等[17]提出的基于LSTM的航迹跟踪.这些方法都可减少虚假航迹数.

本文转换了角度，从雷达数据处理的角度出发，基于动态自适应DBSCAN 聚类算法，结合经典卡尔曼滤波跟踪算法，提出DBSCAN-KALMAN混合算法.该算法包括两个部分，分别是点迹数据精细化处理阶段和目标跟踪阶段.在点迹数据精细化处理阶段，DBSCAN-KALMAN以雷达扫描周期为时间片单位，对各时间片中的点迹数据，应用DBSCAN算法进行聚类，将聚类后的各类点迹数据依据质心算法分别计算点迹质心，以各类点迹数据与各类质心欧式距离最小的点迹作为此时间片最终输出点迹，被DBSCAN标记为噪声点的点迹也作为此时间片最终输出点迹输出；在跟踪阶段，应用经典卡尔曼滤波算法，对于多个时间片内的输出点迹数据进行跟踪处理，形成目标航迹.

三坐标航管一次雷达信噪比、地波干扰会产生大量虚假目标点迹干扰，但其严重程度并不至于干扰民航机等大目标.本方法适用于快速在低空空域范围内发现非合作目标(即没有提前报备的黑飞目标)的场景.利用动态自适应DBSCAN 聚类跟踪混合算法，有效减少杂波造成的虚假点迹，快速跟踪并形成民航飞机与黑飞目标航迹，这样可以及时发现黑飞目标，将对正常民航飞机飞行的干扰降到最低.

2 自适应DBSCAN算法

2.1 算法原理

聚类算法被广泛应用于用户图像[18]、 文本处理[19]等领域.DBSCAN是一种基于密度的聚类算法，该算法不需要事先给定聚类类别数目，不仅可适用凸样本集，也同样适用于非凹样本集.将所有各组紧密相连的样本化为各个不同的类别，就能得到最终的聚类结果.

2.2 DBSCAN密度定义

DBSCAN参数(ε,MinPtrs)用来描述领域的样本分布紧密程度，其中，ε描述某一样本的领域距离阈值；MinPtrs描述某一样本的距离为ε的领域内包含样本个数的阈值.文献[20]给出了DBSCAN具体密度描述关键定义.

2.3 自适应DBSCAN参数设置

DBSCAN聚类结果对ε与MinPtrs取值敏感，人工选取，可能造成聚类不准确.已有不少文献提出若干参数自适应方法. 文献[21]根据数据集在每个维度的密度分布，动态设置ε，但仍需要输入MinPtrs，没有实现聚类的全自动化.Kim等[22]提出AA-DBSCAN算法，基于四叉树的新树结构来定义数据集的密度层，以实现不均匀密度数据集的聚类，但算法仍需输入相关参数.Khan等[23]提出的AD-DBSCAN自适应聚类算法需要提前指定簇的数量，无法自动识别簇类数目.夏鲁宁等[24]提出的SA-DBSCAN聚类算法，利用逆高斯拟合KNN分布并分解峰值点以确定ε.

本文采用文献[25-26]的DBSCAN自适应参数方法，绘制K-距离曲线与数据点距离升序曲线，取K-距离曲线的第一个谷底位置与数据点距离升序曲线最密集的位置对应的距离的中间值作为ε，而根据雷达跟踪目标飞行特性来确定MinPtrs.

雷达目标跟踪是通过相关和滤波处理建立起目标的运动轨迹，包括对目标运动状态所做的估计和预测，进而对目标进行评估.雷达跟踪最重要的环节就是建立航迹时选用的滤波算法，选用合适的滤波算法可以影响雷达跟踪精度.最常用的滤波算法就是卡尔曼滤波算法.卡尔曼滤波算法主要由以下公式组成[27].

状态一步预测如下式.

(1)

协方差一步预测如下式.

P(k+1|k)=F(k)P(k|k)F′(k)+Q(k)

(2)

量测的预测协方差为

S(k+1)=H(k+1)P(k+1|k)H′(k+1)+

R(k+1)

(3)

卡尔曼增益如下式.

K(k+1)=P(k+1|k)H′(k+1)S-1(k+1)

(4)

状态更新如下式.

K(k+1)v(k+1)

(5)

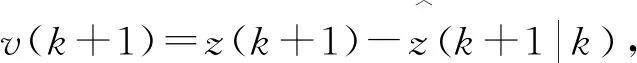
4.1 DBSCAN-KALMAN算法定义

4.1.1 点迹数据划分时间片 由于三坐标航管一次雷达点迹录取器中录取到的点迹是以雷达扫描周期为单位，因此点迹属于时间序列数据，所以需要以雷达扫描周期为时间片单位将点迹集合分成若干小的时间片点迹集合.以下是数学公式描述.

f[T,t0,X(t,x,y,z)]=P(t,n,xn,yn,zn)

(6)

其中,T为雷达扫描周期；t0为初始时刻；t为各点迹录取时刻；X(t,x,y,z)为录取器录取到的点迹数据；n为时间片数；P(t,n,xn,yn,zn)为根据T为单位划分的第n个时间片点迹集合.

4.1.2 基于时间片聚类 理论上同一目标在不同时间片点迹集合中仅会有一个点迹信息，但实际上由于存在虚警与大目标跨越多个距离及方位单元情况，同一目标在相同时间片点迹集合中存在多个点迹信息.

但同一目标在相同时间片点迹集合中的不同点迹之间本身属性差异并不大，在空间分布上符合按密度堆积，即同一目标的不同点迹间通常聚集形成密度稠密的类簇，不同目标间的点迹一般相隔较大，密度稀疏，不会形成类簇.

基于以上特点，使用基于密度的典型聚类方法DBSCAN算法，对时间片点迹集合进行聚类，会形成不同类簇集合.以下是数学公式描述.

g[P(t,n,xn,yn,zn),ε,MinPtrs]=

Y(t,n,c,xc,yc,zc)

(7)

其中,ε为DBSCAN的半径阈值；MinPtrs为DBSCAN的样本阈值；Y(t,n,c,xc,yc,zc)为第n个时间片聚类后第c类的点迹集合.

4.1.3 基于时间片的各类簇计算质心 根据上一步得到类簇集合，以及同一类簇集合间的各点迹间属性差异不大的特点，且聚类后的类簇是同一类目标，因此只需要选择这些点迹集合中的一个点迹代表此类簇即可，这样可以使用于之后的航迹跟踪的候选点迹数量减少.

随机选取同一类簇集合的点迹代表此类簇，会为最终的航迹跟踪结果引入了随机性，所以需寻找一个基准，以此基准来选择哪个点迹代表本类簇.

考虑到点迹信息包括距离、方位、俯仰三个维度及聚类后形成的类簇质心表征本类属性的特点，所以对这三个维度分别取质心，即分别取三个维度的中心，并组成最终基准.以下是数学公式描述基准的形成.

Y(t,n,c,xc,yc,zc)=

Z(t,n,c,xcenter,ycenter,zcenter)

(8)

其中,Z(t,n,c,xcenter,ycenter,zcenter)为使用质心算法后第n个时间片聚类后第c类质心点迹.

4.1.4 基于时间片的各类簇点迹选择 根据上一步计算得到的各类簇基准，以与基准的欧式距离最小的各类簇点迹来代表各类簇.以下是数学公式描述.

Dis[Y(t,n,c,xc,yc,zc),Z(t,n,c,xcenter,ycenter,zcenter)]=

(9)

Y′(t,n,c,xc,yc,zc)=Min{Dis[Y(t,n,c,xc,yc,zc),

Z(t,n,c,xcenter,ycenter,zcenter)]}

(10)

我们选取使Dis最小的对应的点迹Y′(t,n,c,xc,yc,zc)作为此时间此类的最终点迹.

4.1.5 卡尔曼滤波航迹跟踪 经过以上步骤，将所有基于时间片得到的点迹作为候选点迹集合进行航迹跟踪，得到不同目标形成的点迹集合，即航迹.以下是数学公式描述.

H[Y′(t,n,c,xc,yc,zc)]=Ti(t,xc,yc,zc)

(11)

其中,Ti(t,xc,yc,zc)为卡尔曼滤波跟踪到的第i条航迹的点迹集合.

4.2 基于自适应DBSCAN的雷达目标跟踪算法实现

基于自适应DBSCAN的雷达目标跟踪算法的主要步骤如算法1所示.

算法1基于自适应DBSCAN的雷达目标跟踪算法

输入：三坐标航管一次雷达某一时间段点迹集X(t,x,y,z)，待雷达目标跟踪点迹空队列Queue.

输出：跟踪到的各条航迹对应的点迹集合Ti(t,xc,yc,zc).

Begin

Step1通过分析某一时间段的雷达录取器中的点迹分布，确定DBSCAN的阈值MinPtrs，并在所有时间片聚类过程中保持不变；

Step2将点迹集拆分成多个以雷达扫描周期为单位的时间片集合τ(t1、t2，…)，对每个时间片绘制出K-距离曲线与数据点距离升序曲线，取K-距离曲线的第一个谷底位置与数据点距离升序曲线最密集的位置对应的距离的中间值，作为此时间片的DBSCAN的半径ε；

Step3对时间片ti进行DBSCAN聚类；

Step4对Step 3聚类完成后形成的非噪声类簇求质心，质心属性使用下面公式分别求解：

距离属性：

(12)

方位属性：

(13)

俯仰属性：

(14)

Step5选择此类簇中点迹与其质心点迹欧式距离最小对应的点迹作为此类簇最终点迹输出，并添加到待目标跟踪点迹队列Queue中；

Step6对Step 3聚类完成后形成的噪声类不做处理，直接添加到Queue中；

Step7重复Step 2～Step 6步骤，直到全局聚类；

Step8将Queue的点迹作为雷达目标跟踪算法输入数据进行跟踪.

End.

5 实 验

表1 三坐标场面监视一次雷达部分点迹数据

5.1 雷达聚类前点迹分布

文章使用三坐标航管一次雷达于2019年4月29日在南充某机场录取到的点迹数据作为分析依据，聚类前雷达点迹数据分布，如图1所示.

图1 聚类前雷达点迹数据分布

5.2 雷达聚类前航迹跟踪结果

经过航迹起始、跟踪、滤波、平滑处理后，跟踪到多条航迹.从聚类前跟踪的航迹明显可以看出，航迹存在分叉、虚假航迹、部分航迹长度很短等干扰情况，航迹分布如下图2所示.

图2 聚类前雷达跟踪到的航迹

5.3 基于自适应DBSCAN的雷达点迹跟踪

5.3.1 雷达扫描周期内进行点迹聚类 选择点迹数最多的一个雷达扫描周期作为分析区间.使用Matlab计算得到一个雷达扫描周期内最多有62个点迹，位于第298个时间片位置.

本文选择K= 4.计算排序的4-距离曲线图与数据点距离升序曲线，如图3和图4所示.

图3 4-距离曲线图

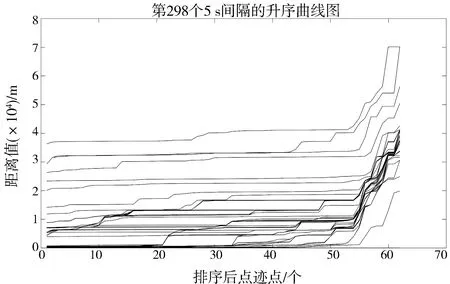
图4 数据点距离曲线

根据文献[10-11]提出了自适应DBSACN的参数配置方法与改进方法，确定第298个时间片的DBSCAN参数分别为设置ε= 100与MinPtrs= 4，距离采用欧式距离,求类簇中心属性使用本文提出的质心属性求解公式.聚类运行结果如图5所示.聚类结果如表2所示.

图5 自适应DBSCAN聚类结果

5.3.2 点迹跟踪 全局聚类后对所有时间片输出点迹进行航迹跟踪.实验表明，跟踪后的航迹质量提高，杂波点进一步减少，运算速度提高，跟踪后航迹分布如图6所示.

表2 聚类结果表

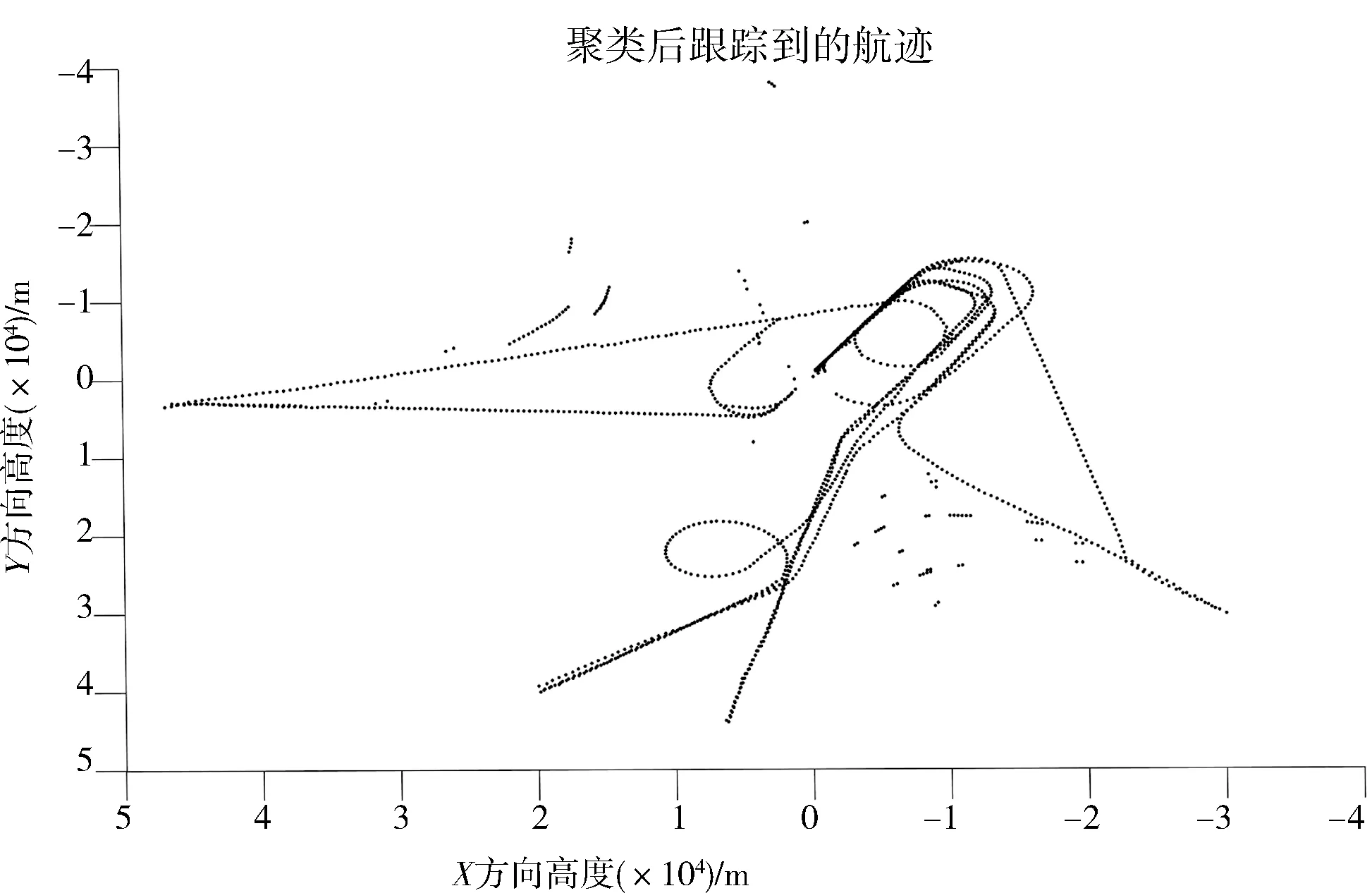
图6 聚类后雷达跟踪到的航迹

实验对聚类前后结果进行了简单对比，对比如表3所示.

表3 聚类前后对比表

对比以上结果表明，运用提出的混合算法有一定的有效性，能减少无效点迹，航迹质量也得到了提高，但被DBSCAN标记为噪声类的点迹集合中存在小部分有效点迹，为了保证不丢失任何有效点迹，保留所有噪声类点迹并输出，这是限制此算法效果的主要因素.因此需要继续优化算法，将噪声类点再进行细分，将真实的噪声点滤除掉，以达到最优效果.

6 结 论

本文有效解决了雷达点迹形成航迹过程运算量大、形成虚假航迹多、航迹质量不好等问题.对每个扫描周期进行自适应DBSCAN聚类，减少了每个扫描周期内点迹数.使用质心算法计算聚类后各类簇质心，选择使该类质心与该类点迹的欧式距离最小的点迹及被标记为噪声点的点迹作为该类点迹输出，并对所有时间片输出点迹进行航迹跟踪.航迹跟踪后表明无效点迹减少，航迹质量提高，跟踪时间缩短.而如何继续减少无效点迹点，仍然是未来雷达领域的研究主要方向.