An asymptotic formula for the gcd-sum function of Jordan’s totient function
-, -,
(1.School of Mathematics, Sichuan University, Chengdu 610064, China;2. School of Mathematics and Computer Science, Panzhihua University, Panzhihua 617000, China)
Abstract: Let gcd(k,j) denote the greatest common divisor of the positive integers k and j, r be any fixed positive integer. Let Mr(x;f) where x≥2 is any large real number and f is any arithmetical function. Let Jk denote Jordan’s totient function defined for any integer n≥1 by Jk(n) In this paper, by using the identity of Kiuchi on Mr(x;f) together with some analytic techniques, we present an asymptotic formula of Mr(x;Jk). These complement and strengthen the corresponding results obtained by Kiuchi and Saadeddin in 2018.
Keywords: Gcd-sum function; Jordan’s totient function; Mean value; Partial summation; Riemann Zeta-function
1 Introduction
Let gcd(k,j) be the greatest common divisor of the integerskandj. The gcd-sum function, which is also known as Pillai’s arithmetical function, is defined by

This function has been studied by many authors such as Broughan[1], Bordelles[2], Tanigawa and Zhai[3], Toth[4], and others. Analytic properties for partial sums of the gcd-sum functionf(gcd(j,k)) were recently studied by Inoue and Kiuchi[5]. We recall that the symbol * denotes the Dirichlet convolution of two arithmetical functionsfandgwhich is defined by
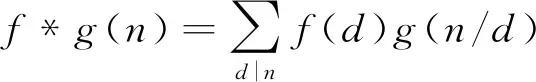
for every positive integern. For any arithmetical functionf, Kiuchi[6]showed that for any fixed positive integerrand any large positive numberx≥2,

(1)
Here, as usual, the functionμdenotes the Mobius function,
Bm=Bm(0) is a Bernoulli number, whereBm(x) is a Bernoulli polynomial defined by the generating function
with|z|<2. Many applications of (1) have been given in Refs.[6-8]. Some related results are refereed to Refs.[9-11].
Letkbe a positive integer. In number theory, Jordan’s totient functionJkis defined by

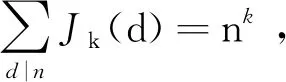
Theorem1.1Letabe a positive integer >1. Then for any fixed positive integerrand any large positive numberx>5, we have
2t+1))xa+1+O(xa).
2 Preliminaries
Lemma2.1(i) Letτ=1*1 be the divisor function. Then for any large positive numberx, we have
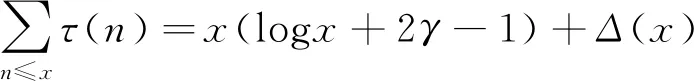
(2)
whereγis the Euler constant and error termΔ(x) can be estimated byΔ(x)=O(xθ+), it is known that one can take
(ii) Letσu=idu*1 be the generalized divisor function for any real numberuand leta≥1 be an integer. Then for any large positive numberx≥2, we have
(3)

(iii) For any large positivenumberx>5, we have
(4)
(5)
(6)

Proof(2) is Theorem 7.3 of Ref.[12],(3)~(6) follow from Ref.[13].
Lemma2.2Letkbe an integer withk>1. Then for any large positive numberx>5, we have
(7)
(8)
(9)
Proof(7) and (8) are shown in Ref.[5]. Now let us show (9). Since
it follows that

Therefore by partial summation and (7), one has

as claimed. This completes the proof of the claim.
Sinceδ(x) is monotonic decreasing, it follows from the claim that
Finally, one deduces that
Thus (9) is true. Lemma 2.2 is proved.
Lemma2.3Letabe a fixed number with 1
(10)
ProofWe use partial summation withf(n)=1 andg(t)=xa. ThenF(t)=[t] andg′(t)=ata-1. Thus
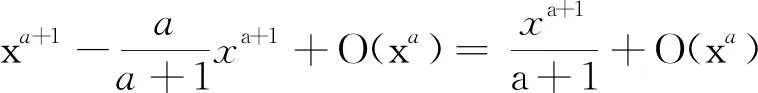
as required. This completes the proof of Lemma 2.3.
Lemma2.4[14]Letm,tbe a fixed real number withm>1 andt>1. Then for any sufficiently large numberx>2, we have
(11)
Lemma2.5Leta>1 be a positive integer. For any large positive numberx>5, we have
ProofSinceJk=μ*idk, we have
Hence

By (10), one gets that

as desired. This finishes the proof of Lemma 2.5.
Lemma2.6Leta>1 be a positive integer. For any large positive numberx>5, we have
ProofSinceJk=μ*idk, one has

By (3), we derive that
By (9), we derive that
as required. The proof of Lemma 2.6 is complete.
Lemma2.7Lettbe an any positive integer. For any large positive numberx>5, one has
ProofSinceJ1+a=μ*id1+a, one has
It follows that
Then we can deduce that
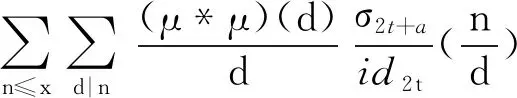

Then, by (11), we obtain that
By (9), we get that
This concludes the proof of Lemma 2.7.
3 The proof of Theorem 1.1
Lettingf=J1+ain (1) gives us that

J1+J2+J3
(12)
where

From Lemmas 2.5 to 2.7 one has
(13)
(14)
(15)
Putting (13) to (15) into (12), the desired result follows immediately.This finishes the proof of Theorem 1.1.

