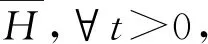无限维空间上的波方程和Schrödinger 方程解的存在性和唯一性
梁冬冬
(四川大学数学学院, 成都 610064)
1 引 言
设H为无限维可分的复Hilbert空间,u为定义在H上的泛函.类似于有限维空间上的偏微分方程,我们也可以建立一个以u为未知函数的H上的偏微分方程.我们称这样的微分方程为无限维空间上的偏微分方程. 这一类微分方程来源于量子场论、晶体的固态理论及具有无限多个自由度的系统、无限维随机控制理论等[1-8].
在有限维空间中,我们可以利用概率论的方法研究偏微分方程,推广这种方法也可以去研究无限维空间的偏微分方程. 比如:文献[2-3] 利用随机微分方程得到了无穷维空间中的线性抛物偏微分方程的解,即Feynman-Kac 表示. 文献[4]利用正、倒向随机微分方程将线性Feynman-Kac 公式推广到了非线性抛物方程的情形. 文献[5]推广了这种方法,并利用非耦合的正、倒向随机方程得到了无穷维空间的半线性抛物方程的初值问题的mild解,进而利用动态规划方法研究了对应的随机最优控制问题.
另一方面,有界开集上的无限维空间中的抛物偏微分方程的初边值问题也引起了部分学者的关注.例如文献 [6] 利用停时对正向随机微分方程的解过程做了反射,得到了有界开集上的无穷维空间上的线性抛物偏微分方程的齐次边值问题解的存在唯一性.然而,非齐次方程的边值问题还未解决.当前,无限维空间中的微分方程的研究多局限在研究空间中的抛物方程.利用这种方法获得的较好的结果见文献[7],该文解决了耦合的正倒向随机方程的适定性问题,并利用正、倒向随机微分方程的解来表示无穷维的HJB 方程. 但是,用这种方法,解的表示公式越来越复杂,因而可以求解的偏微分方程的类型受到了极大的限制,比如本文中的无限维空间的波方程和Schrödinger 方程就无法求解. 由于无限维椭圆方程的L2理论不完善,本文利用Guassian-Sobolev 空间,结合关于椭圆方程的假设条件,使用半群方法得到了无限维空间中的波方程和Schrödinger 方程解的存在性、唯一性.
2 预备知识
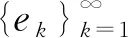
(1)
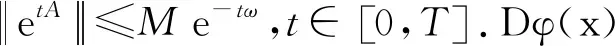

以L2(H,μ)表示H上在测度μ下平方可积的函数全体,∀φ,ψ∈L2(H,μ),在L2(H,μ)中定义内积
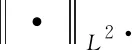
定理 2.1[8]对任意x,y∈D(A),Q∞是唯一的使得下列等式成立的算子.∀x,y∈D(A*),
〈Q∞x,A*y〉+〈Q∞A*x,y〉=-〈Qx,y〉.
令EA(H)=span{e〈h,x〉;h∈D(A*)}.由测度的 Fourier 变换可得EA(H)在L2(H,μ)中稠密.
定义2.2任意k∈N,定义映射
Dk:EA(H)⊂L2(H,μ)→L2(H,μ),φ→Dkφ,
以L2(H,μ;H)表示H上所有的H-值的在测度μ下平方可积的映射全体. ∀φ,ψ∈L2(H,μ;H), 以如下方式定义内积:

则L2(H,μ;H)在以上内积下是一个Hilbert 空间.
定义2.3以如下方式定义算子
D:EA(H)⊂L2(H,μ)→L2(H,μ;H),
引理 2.4[8]任意φ,ψ∈EA(H),∀k∈N,有下列等式成立:
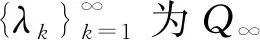
引理 2.5[8]任意k∈N,Dk和D为可闭算子.
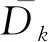
定义2.6∀φ,ψ∈Dom(D),定义内积如下:
则Dom(D)在这个内积下是一个Hilbert 空间,称为Sobolev 空间,记为W1,2(H).
以L2(H,μ;L2(H))表示H上的在μ测度下平方可积的L2(H)-值映射全体,L2(H)表示H上所有的Hilbert-Schmidt 算子全体.∀φ,ψ∈L2(H,μ;L2(H)),在L2(H,μ;L2(H))中以如下方式定义内积:

定义2.7按如下方式定义映射D2,
D2:EA(H)⊂L2(H,μ)→L2(H,μ;L2(H)),
φ→D2φ,
其中D2φ为φ的二阶导数,作用为:∀α,β∈H,
αk,βh分别表示α,β在H的基下的坐标.

〈φ,ψ〉W2,2=〈φ,ψ〉W1,2+〈D2φ,D2ψ〉L2(H,μ;L2(H)),
则Dom(D2)∩Dom(D)在这个内积下为一个Hilbert 空间,记为W2,2(H). 注意到空间W2,2(H)中的函数的二阶导数关于测度μ在几乎处处的意义下只是一个Hilbert-Schmidt 算子.
定义2.8定义算子DQ如下:
DQ:EA(H)⊂L2(H,μ)→L2(H,μ;H),
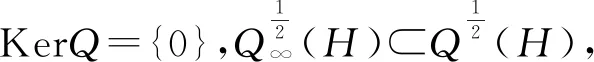

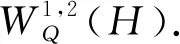
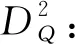
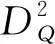
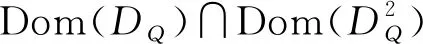
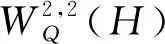
∀x∈H
(2)
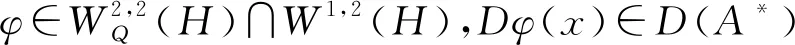

∀φ,ψ∈EA(H),以如下方式定义内积:
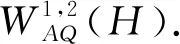
定义2.12按照如下方式定义一个算子
φ→Lφ,

引理 2.13[8]对任意φ,ψ∈EA(H),以下等式成立:
∀φ∈EA(H),不妨设φ(x)=e〈h,x〉,h∈D(A),
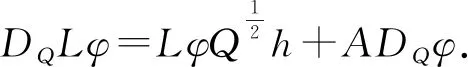
两次利用引理2.13 的(ii)容易得到

定义2.14在空间EA(H)中按照如下方式定义范数.∀ψ∈EA(H),
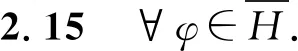
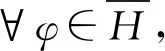
因而
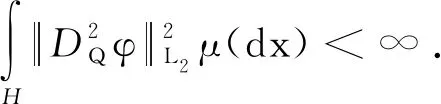
〈x,ADφ(x)〉)|μ(dx)≤
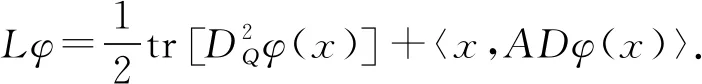
3 椭圆方程弱解的存在唯一性
考虑如下方程,∀g∈L2(H,μ), ∀x∈H,
(3)
利用算子L将方程(3)形式地写成
Lφ=g
(4)
注意到方程(3)和(4)本质上不是同一个方程.算子L的作用方式一般不是方程(3)的左边项的形式.然而它们的解之间确实有着很强的关系.
若φ∈S满足方程(4),在(4)式两边乘以ψ后在H上积分得
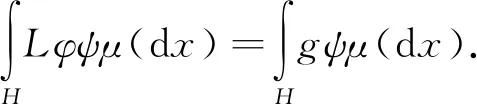
左边项利用引理2.13式(ii)知∀ψ∈S,
(5)
反之,若存在φ∈S满足式(5),由引理 2.13(ii)得

由S在空间L2(H,μ)中的稠密性得(4).
定义3.1设g∈L2(H,μ).φ∈S称为方程(4)的解,若任意ψ∈S,φ满足积分恒等式(5).
在无穷维空间中,椭圆方程的解很难直接得到,主要原因在于无穷维空间上椭圆的能量估计一般不成立.而且,在何时成立着能量估计也尚不清楚. 本文在椭圆方程的解的基础之上去研究波方程和Schrödinger方程.
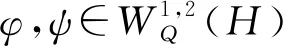


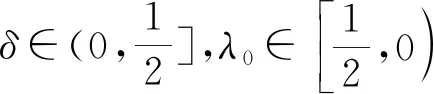
证明 由范数和双线性函数F的定义,容易得到结论.
定理3.5对任意g∈L2(H,μ),λ∈C, Reλ≥λ0,方程(4)有唯一弱解.
证明 根据命题3.4,利用Lax-Milgram定理易
得定理3.5的结论.
当方程(4)的弱解正则性足够高时,弱解就是定义3.1中的解了. 然而遗憾的是,无论是(4)的解还是弱解,都不是方程,g∈L2(H,μ),
(6)
的解,即几乎处处的x∈H满足方程(6).

证明 由命题2.15易得.
4 波方程弱解的存在唯一性
接下来,我们考虑如下形式的波方程,
(7)
应用前文所定义的算子L,我们将方程(7)形式上写成下列方程:
(8)
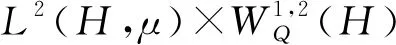
u=(u1,u2)T,φ=(φ1,φ2)T.
定义算子G如下:
u→Gu,
其中

进一步,利用算子G将方程(8)写成下式:
在M中重新定义内积如下:∀u1,u2∈M,设u1=(u11,u12)T,u2=(u21,u22)T,则
〈u1,u2〉=〈u11,u21〉L2+〈u12,u22〉L2+
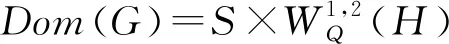
假设4.1令λ∈C.方程λω-Lω=f的弱解ω满足:
(i)f∈L2(H)时,ω∈S;
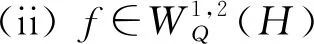
(i)f∈S时,ω∈D((L)2).
注意到当H是一个有限维空间时,假设4.1就是椭圆方程弱解的正则性,成立;当算子Q和A均是有限秩算子,且二者的值域空间相同时,由偏微分方程弱解的正则性易知假设4.1也成立.
引理4.2若假设4.1中成立,则对任意F=(f1,f2)T∈M,λ∈C,Reλ2≥λ0,|λ|>1,方程(λI-G)U=F有唯一解U∈S,且解U满足估计式.
证明 ∀F=(f1,f2)T∈M,令U=(u1,u2)T.方程(λI-G)U=F等价于
设方程λ2I-Lωi=fi的弱解为ωi.则ωi∈S,i=1,2. 令u1=λω1+ω2,u2=λω2+Lω1.则U=(u1,u2)T为方程(λI-G)U=F的解. 事实上,我们有
λu1-u2=λ2ω1+λω2-λω2-Lω1=
λ2ω1-Lω1=f1,
λu2-Lu1=λ2ω2+λω1-λω1-Lω2=
λ2ω2-Lω2=f2.
因此,∀λ∈C,Reλ2≥λ,λI-G为满射.
对任意F=(f1,f2)T∈S×S,λ∈C,|λ|>1,方程(λI-G)U=F的解U=(u1,u2)T∈S×S.为计算方便,将L2(H,μ)和L2(H,μ;H)中的内积简记为〈·,·〉则
〈f1,f2〉-〈Lf1,f1〉+〈f2,f2〉=
〈f1-Lf1,f1〉+〈f2,f2〉=
〈λu1-u2-λLu1+Lu2,λu1-u2〉+
〈λu2-Lu1,λu2-Lu1〉≥
|λ|2〈u1,u1〉-2Reλ〈u1,u2〉+
(1+|λ|2)〈u2,u2〉-
|λ|2〈Lu1,u1〉+〈Lu1,Lu1〉-〈Lu2,u2〉≥
|λ|2〈u1,u1〉-2|λ|〈u1,u2〉+
〈Lu1,Lu1〉-〈Lu2,u2〉≥
(|λ|2-|λ|)〈u1,u1〉+
(1+|λ|2-|λ|)〈u2,u2〉+

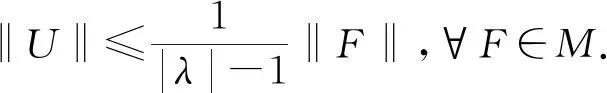
定理 4.3当假设4.1成立时,算子G能生成M上的一个C0半群{T(t)}t≥0,满足‖T(t)‖≤et,∀t≥0.
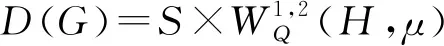
所以G能生成C0半群{T(t)}t≥0.证毕.

证明 设T(t)是G所生成的C0半群.令
(u1,u2)T=T(t)(φ1,φ2)T,
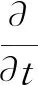
则u1为(8)的解.
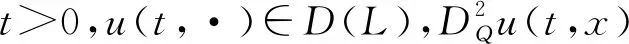

考虑方程
(9)
利用算子L将方程(9)形式上写为下列方程:
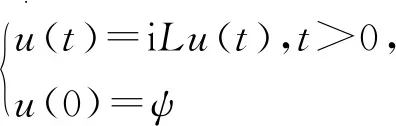
(10)
定理5.1当假设4.1中的 (i) 成立时,iL能生成L2(H,μ)上的一个C0半群.
证明 因EA(H)⊆Dom(L)=Dom(iL),则S在L2(H,μ)中稠密,这里Dom(iL)表示iL的定义域.由引理 2.13(ii),得Re
推论5.2在定理5.1 的条件下,方程(10)存在唯一解u∈C1([0,∞),S).