基于SOM神经网络聚类和灰度TOPSIS评价法的岩爆预测

田 冰，黄 山，孙 晔，闫宇杰，金康康

(1.华北理工大学以升创新教育基地，河北 唐山 063210；2.华北理工大学人工智能学院，河北 唐山 063210；3.北京电信规划设计院有限公司，北京 100044)

0 引 言

岩爆是地应力条件下深部工程和开采过程中的一种人为地质灾害，围岩应力进行重新分布，引起该地区短时间内产生猛烈、突发的破环现象。岩爆严重威胁施工人员和设备的安全，甚至会诱发地震，因此对岩爆发生的客观精准预测尤为重要。随着近年来我国对工程安全的重视，很多学者对岩爆预测展开了研究。

理论分析法是常用的预测方法，包括煤岩冲击倾向性法、综合指数法、数值模拟法。目前，国内外学者将机器学习引入到岩爆预测中，如模糊数学法、粒子群算法和广义神经网络、贝叶斯判别分析、支持向量机等[1-2]，改进了单一判据的岩爆预测方法并且成功应用于实际生产中。贾义鹏[3]提出一种基于粒子群算法优化的广义神经网络岩爆预测模型，减少了主观因素对神经网络设计的影响;李宁等[4]提出基于粗糙集理论和支持向量机的岩爆预测;刘冉等[5]提出粗糙集-多维正态云模型岩爆分级预测，具有较好的实用性。但是由于机器学习自身的局限性，如所需样本数量大且易过拟合、参数设定无标准造成结果不同等，导致计算复杂、实用性低的问题，且在指标权重确定上具有较强的主观性。本文针对性地选取预测指标，从应力、岩性、能量三个角度出发，通过SOM神经网络先对样本进行聚类分析，再结合灰色关联度计算应力、岩性、能量三个指标因素的权重，最后采用TOPSIS评价法对聚类结果进行排序预测。这种预测方法较好地解决了当前岩爆理论预测中存在的不足，并得到了较好的实验结果。

1 岩爆的主要因素和现有判据方法

岩爆产生大体可分为外因和内因两方面。外因是指由于在岩石中开挖洞室造成的岩体赋存空间环境的改变。内因主要是由于岩性的不同，岩爆一般发生在硬岩条件下，由于岩体所储存的弹性变形能不能满足岩体变形所消耗的能量，使得岩块被剥离出去以动能的形式释放。通过分析岩爆产生的内因和外因，综合上述选取最大切向应力σθ与单轴抗压强度σc之比σθ/σc,岩石单轴抗拉强度与抗压强度之比σc/σt,弹性能量指数Wet三个指标，分别从应力、岩性、能量三个不同角度对岩爆等级进行预测。其判据方法见表1[1]。

表1 判据准则表Table 1 Criterion rules

本文研究目的是从多个不同角度对岩爆进行精准预测，需要对指标选取是否合理进行检验。通过对样本指标数据的KMO检验，验证应力、岩性、能量三个指标选取合理，不存在信息的冗余。样本数据见表2。

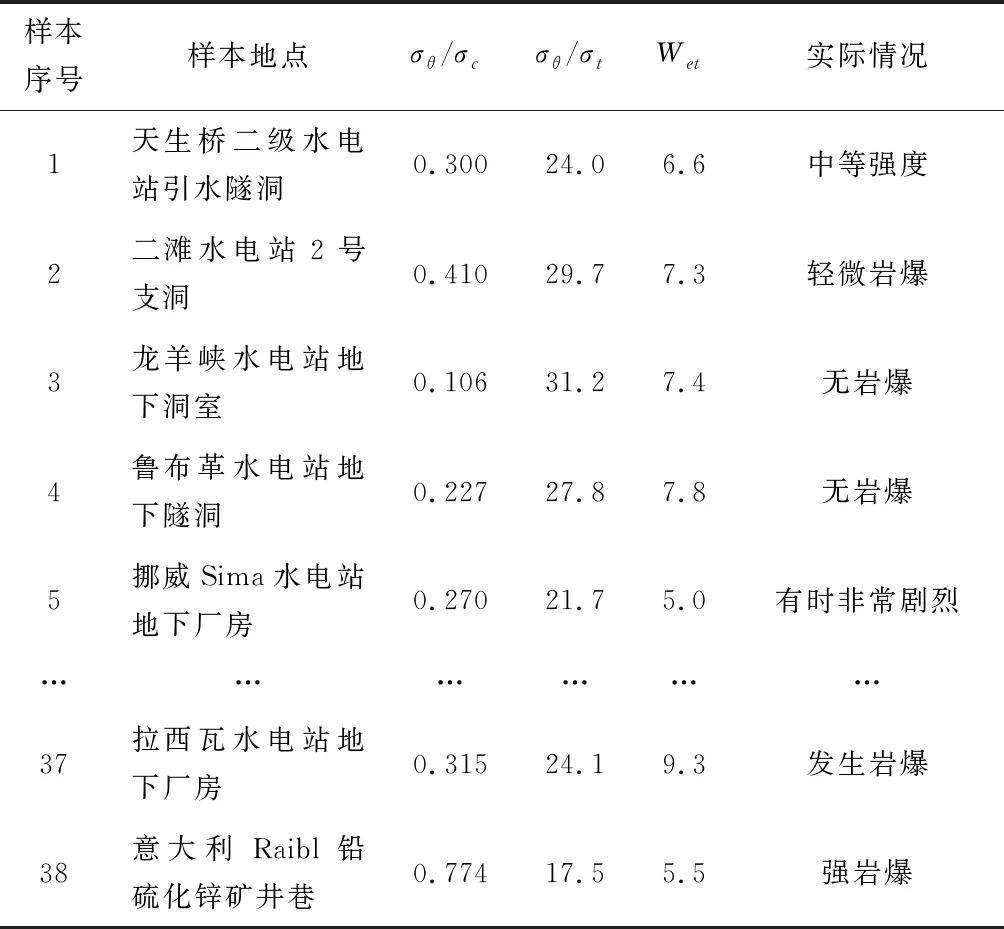
表2 样本数据Table 2 Sample data

将表2中38组样本的三个指标数据通过SPSS进行KMO检验，得到KMO值为0.413，对比Kaiser给出的常用KMO度量标准，发现三个指标应力、岩性、能量之间信息冗余很少，相对独立，进而验证不同方向指标的选取合理性(表3)。

表3 KMO和巴特利特检验结果Table 3 KMO and Bartlett test results

2 SOM神经网络聚类

由于相同岩爆等级下的样本会在某些特征指标存在很大的近似，符合聚类本质“物以类聚”，所以采用聚类的方法对样本归类。岩爆程度分为四个等级，所以聚类类别数目应为4类。以不同方向的三种指标应力、岩性、能量作为输入神经元，通过自组织特征映射网络SOM算法将样本进行归类。

该聚类方法通用的距离有欧氏距离法和余弦法两种，两种距离代表的意义不同，本文选取欧氏几何距离法，X为岩爆指标因素，计算见式(1)。

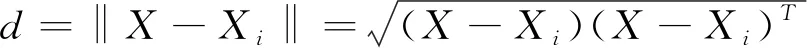
(1)

采用最大最小值标准化，也称为归一化，对输入神经元数据进行线性变换，使其映射至[0,1]之间，转换函数见式(2)。

(2)

对数据进行归一化处理后按以下步骤进行SOM神经网络聚类。

1) 初始化：每个节点根据随机值初始化参数，每个节点的参数数目应与输入层的维数相同。

2) 对于每一个输入数据，在迭代时找到与它最相配的节点。因为输入是三维的，即X={x1,x2,x3},由式(1)可知判别函数。找到对应的激活节点I(x)之后，令Sij表示节点i与节点j之间的距离，对于I(x)相邻的节点，分配给它们一个新的权重，计算见式(3)和式(4)。

诺贝尔文学奖得主赫尔曼·黑塞激赏的长篇小说，自六十年代至今已被译成四十多种文字在全球发行。《鹿》极具艺术性地描写了女性命运，以及女性自我价值实现的意义。

(3)

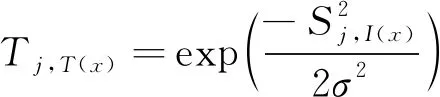
(4)

3) 相邻的节点根据欧式距离的远近使更新大小不一样。按照梯度下降法更正节点的参数，迭代，直到收敛，计算见式(5)。

Δwji=η(t)×Tj,I(x)(t)(wi-wji)

(5)

通过Matlab软件制作SOM神经网络可视化聚类拓扑图如图1和图2所示。由图1和图2可知，四个拓扑节点数即聚类类别数为4个，每两类之间的相对距离即相似度由颜色深浅体现，颜色越深说明两类之间的差异越大，导出聚类结果并进行检验分析(表4)。图2反映出SOM聚类效果，图中圆点较为离散说明聚类效果较好。图1中类别Ⅰ与类别Ⅳ之间为黑色，说明两者差距最大，类别Ⅰ与类别Ⅲ之间为白色，颜色最浅，说明两者更为贴近。

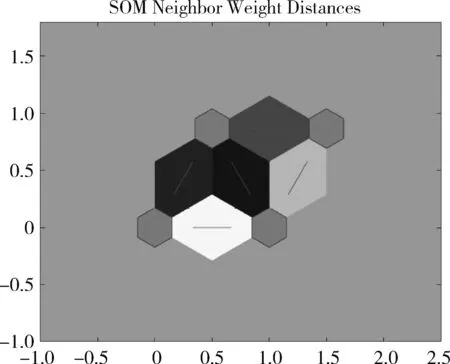
图1 SOM神经网络拓扑聚类相似度Fig.1 SOM neural network neighbor distances

图2 SOM神经网络拓扑聚类权重分布Fig.2 SOM neural network weight position

表4 SOM神经网络聚类结果Table 4 SOM neural network clustering results

3 灰色关联度定权

以灰色关联度定权的方法为后续多信息融合判定岩爆等级模型确定权值。为确定各项指标对岩爆程度等级的影响，首先需要把岩爆等级无岩爆、弱岩爆、中等岩爆、强岩爆离散数值化为1、2、3、4。选取岩爆等级作为参考数列，之后根据式(6)和式(7)对指标数值进行标准化处理，消除量纲的影响。由于指标的正负相关性不同，正相关指标应力、能量标准化处理选择式(6)，负相关指岩性标标准化处理选择式(7)。

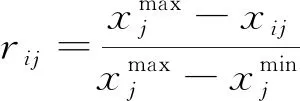
(6)

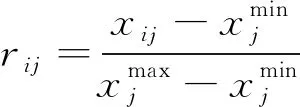
(7)

计算关联度系数ζi(k),分辨系数ρ取0.5，见式(8)。

ζi(k)=

(8)

通过Matlab软件进行计算并可视化展示计算结果如图3所示。由图3可知，影响岩爆程度的因素由大到小排序为应力、岩性、能量，关联度分别为0.450、0.368、0.345。根据式(4)对关联度进行归一化处理，各个指标的归一化权重分别为0.387、0.316、0.296。

图3 灰色关联度可视化Fig.3 Visualization of grey correlation degree

4 TOPSIS评价类别分级

在上述过程中，已经将18组样本进行类别划分,并通过灰色关联度将应力、岩性、能量三个指标对岩爆产生的影响程度以数值体现，通过归一化处理求得权值。聚类分析算法仅能将具有相似性的样本进行归类，并不能直接预测岩爆程度等级，所以需要寻找一种较为客观的评价类算法来对其进行精准预测。TOPSIS评价法是根据有限个评价对象与参考目标的接近程度进行分析的方法，通过TOPSIS法计算得到各类别与理想化目标的贴近度，来实现对类别的排序，进而实现对岩爆程度等级的预测。计算步骤如下所述。

1) 设岩爆等级决策矩阵A=(aij)m×n,列写岩爆等级决策矩阵可由各项指标判据方法得出。在第3部分灰色关联度定权中将岩爆等级程度以1～4数值化，将每一类中样本的应力、能量、岩性判据岩爆程度等级求取数学期望，每个样本具有同等地位，即每个样本的权值相等。根据应力、岩性、能量判据方法以及岩爆程度等级离散值化。Aij为第i类样本从j指标的岩爆等级数学期望，j从1～3分别对应应力、岩性、能量，i从1～4分别对应第Ⅰ类～第Ⅳ类，得到岩爆等级决策矩阵A，见式(9)。

(9)

2) 评价值进行标准化处理，设标准化决策矩阵B=(bij)4×3,见式(10)。

(10)

3) 构建加权的标准化矩阵C=(cij)4×3,其中，cij=w×bij,i=1,2,3，4;j=1,2,3；w为灰色关联度求权归一化处理后所得矩阵w=(0.387 0.316 0.296)。

4) 计算岩爆类别的正负理想解，见式(11)和式(12)。

正理想解

(11)

负理想解

(12)

5) 计算各岩爆类别到正负理想解的距离，见式(13)和式(14)。

(13)

(14)

6) 计算综合评价值即贴近度T，见式(15)。

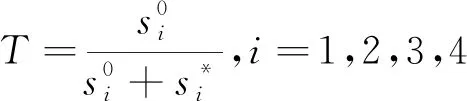
(15)

通过Matlab软件计算出贴近度T为(1.000 0，0.458 0，0.627 4，0.090 4)，将SOM神经网络聚类得到的4类样本通过贴近度进行排序为类别Ⅳ<类别Ⅱ<类别Ⅲ<类别Ⅰ。本次评价以岩爆等级程度较高作为正理想解，所以式(15)也可作为岩爆等级程度比较，将岩爆等级程度与之对应即可实现岩爆预测。

5 实验结果

通过对38个样本按上述过程先进行归类，再通过灰色关联度计算应力、岩性能量三指标的权值，最后采用TOPSIS评价法进行对指标的融合预测，结果见表5。

表5 实验结果与实际情况对比Table 5 Comparison between experimental results and actual conditions

本文精准预测38组样本中的32组样本的岩爆等级，其中，4组出现较小偏差，2组出现较大的偏差。实验结果表明SOM聚类和灰色关联度-TOPSIS模型计算得出的岩爆预测等级与实际情况基本吻合。

6 结 论

1) 本文从岩性、应力、能量三方面选取压拉比σc/σt、切应力与单轴抗压强度比值σθ/σc、弹性应变指数Wet作为预测指标，为减少主观因素的影响，采用灰色关联度计算权重，使岩爆预测的可操作性更强。

2) 结合自组织映射神经元聚类与逼近理想解的排序法(TOPSIS)，根据岩爆预测指标的分级标准构建初始评判矩阵，结合灰色关联度确定的权重构造加权标准化决策矩阵，然后计算出贴近度，最后利用贴近度对聚类的结果进行排序。

3) 提出了一种新的岩爆预测手段，避免了神经网络、支持向量机直接预测带来的调参和过拟合现象，本文进行先聚类再判据的预测方法得到了很好的实验结果。

4) 有预测结果与实际情况对比结果表明，由SOM聚类和灰色关联度-TOPSIS模型计算得出的预测结果与岩爆实际情况基本一致，证实了方法的准确性和有效性。