矿井粉尘浓度预测模型的建立及应用研究
王月红,高 萌,赵帅博
(华北理工大学矿业工程学院,河北 唐山 063210)
矿尘不仅危害井下工作人员的身体,当矿尘达到一定浓度也会引发爆炸,还会造成更严重的井下灾害事故。在煤矿生产作业过程中,如钻井、爆破作业、采煤机及掘进机作业、煤矿的运输转运等多个环节都会产生矿尘[1]。在不同矿井中,由于地质条件、煤的变质程度以及采掘方法、机械化程度等不同,矿尘的产生量也有很大的差异;在同一矿井内,矿尘量也处于动态变化中。为了减小矿尘事故,预测井下矿尘浓度,许多学者进行了相关研究。相关文献表明,学者们主要采用神经网络模型对粉尘浓度进行预测,如:改进的神经网络模型[2]、BP神经网络模型[3]、熵权法RBF神经网络[4]。对矿尘浓度进行预测的同时,也建立了相关模型预测尘肺病。谭强等[5]、王维等[6]基于灰色数列模型GM(1,1)对职业病的发病情况进行预测,时冬青[7]在灰色GM(1,1)模型的基础上结合马尔科夫过程构建灰色GM(1,1)-马尔科夫预测模型探讨该模型在职业病预测领域的应用,王永斌等[8]等建立灰色-广义回归神经网络组合模型,研究该模型对尘肺病预测的准确性。通过对尘肺病进行预测,使煤矿管理人员根据尘肺病的发病情况制定具有针对性的预防措施。
ARIMA模型在尘肺病的预测方面有一定的应用[9],但在粉尘浓度预测方面的研究尚少,本文通过建立ARIMA模型并结合实例,具体分析了ARIMA模型在井下粉尘浓度预测方面的应用。
1 ARIMA模型理论基础
ARIMA模型称为求和自回归滑动平均模型,由博克思(Box)和詹金斯(Jenkins)于20世纪70年代初提出的一种著名时间序列预测方法,所以又称为Box-Jenkins模型、博克思-詹金斯法。 所谓ARIMA模型,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。ARIMA模型根据原序列是否平稳以及回归中所含部分的不同,可分为以下三类:自回归模型(Autoregressive Model,AR模型),滑动平均模型(Moving Average Model,MA模型),自回归滑动平均模型(Auto-Regressive and Moving Average Model,ARMA模型)[10]。
1) AR模型。AR(p)为p阶AR模型,它是仅用时间序列不同滞后项作为解释变量的模型。模型见式(1)。
Yt=φ1Yt-1+φ2Yt-2+…+φpYt-p+et
(1)
式中:φ1,φ2,…,φp为自回归系数;p为自回归阶数,也是模型中解释变量的个数;et为t时刻的误差。
2) MA模型。MA(q)为q阶MA模型,它是仅用误差的不同滞后项作为解释变量的模型,模型见式(2)。
Yt=et+θ1et-1+θ2et-2+…+θqet-q
(2)
式中:θ1,θ2,…,θq为移动平均系数;q为移动平均阶数,即模型中解释变量的个数。
3) ARMA模型。ARMA(p,q)为(p,q)阶ARMA模型,模型见式(3)。
Yt=φ1Yt-1+φ2Yt-2+…+φpYt-p+et+
θ1et-1+θ2et-2+…+θqet-q
(3)
特殊情况,若p=0,模型是移动平均模型,记为MA(q),或ARMA(0,q);若q=0,模型是自回归模型,记为AR(p)或ARMA(p,0)。
ARIMA模型简单,只需通过自身的历史观测值就可反映出未来趋势,在预测过程中需要对非平稳数列进行平稳化处理,模型既考虑了时间序列上的依存性,又考虑了随机波动的干扰性。在获得初步模型以后,可以根据贝叶斯信息准则对比模型的优劣程度,从而选出最优模型,提高模型预测的准确率。
2 粉尘浓度预测ARIMA模型
2.1 原始数据准备与处理
以某矿5424工作面粉尘浓度为原始数据来源,通过拟合时间在9∶31~10∶13之间的22组数据,建立合适的ARIMA模型,用于预测10∶15和10∶17这两个时间点的粉尘浓度,再将预测值与实际值进行比较,进而验证模型的适用性。

表1 原始数据Table 1 Original data
在SPSS软件中导入粉尘浓度与时间数据,再绘制序列图,见图1。
从图1中可以看出,随着时间的推移,粉尘浓度有一定的下降趋势,因此认为该序列不是平稳序列,需要对其进行平稳化处理。此时选用差分的方式对数据进行平稳化处理,这里选择二阶差分,这是由于在后期建模过程中,如果只进行一阶差分,所得模型的拟合程度较低。对数据进行二阶差分并绘制时序图,差分后的数据在某一值上下波动,认为序列平稳,见图2,故ARIMA模型d取2。
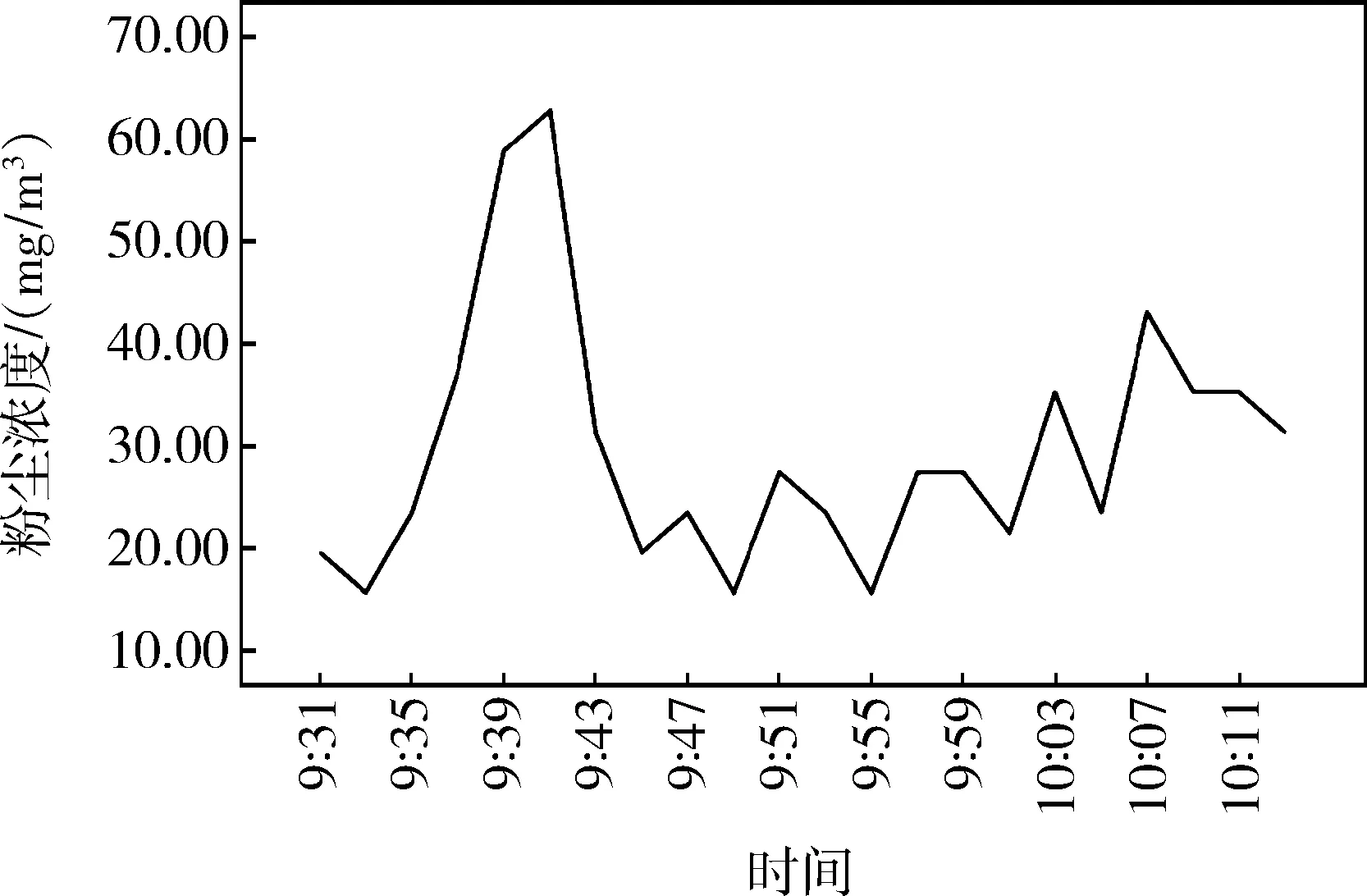
图1 粉尘浓度时序图Fig.1 Sequence diagram of dust concentration

图2 二阶差分时序图Fig.2 Second order difference sequence diagram
2.2 模型识别及参数估计
对于ARIMA模型,如果自相关函数的滞后数为p后截尾,且偏相关函数的滞后数为q后截尾,则其阶数分别为p,q。本文通过自相关与偏自相关系数来确定p值,q值。
通过图3和图4可以看出,图像呈明显的拖尾现象,偏自相关图中滞后编号为1时,偏自相关系数超出置信区间,故p取1。同理,自相关图中滞后编号为1时自相关系数超过置信区间,故q取1。再通过BIC准则,即选取BIC值最小的,BIC值见表2。

表2 BIC值Table 2 Numerical value of BIC

图4 二阶差分偏自相关Fig.4 Second order difference partial autocorrelation

图3 二阶差分自相关Fig.3 Second order difference autocorrelation
根据以上自相关偏相关系数及BIC准则,最后选定ARIMA(1,2,1)最合适。
2.3 模型检验
输出的ARIMA(1,2,1)模型统计量见表3。

表3 ARIMA(1,2,1)模型统计量Table 3 ARIMA(1,2,1) model statistics
由表3可知,模型自由度为16,P值(Sig.)为0.927显著大于0.05的检验水平,因此不能拒绝该序列为白噪声的原假设。由图5分析可得,残差自相关和偏自相关函数均在2倍标准差范围内,因此,认为残差没有相关性,是白噪声序列,进一步验证了模型的合理性。

图5 残差自相关与偏自相关Fig.5 Residual autocorrelation and partial autocorrelation
2.4 模型预测
利用建立的模型对时间在9∶31~10∶13之间的22组数据进行拟合,并对10∶15和10∶17两个时间点的粉尘浓度进行了预测,预测结果见表4。

表4 模型预测结果Table 4 Model prediction results
由表4可以看出建立的ARIMA(1,2,1)模型对10∶15和10∶17两个时间点的粉尘浓度的预测与实测值相差不大,相对误差最大为8.34%,最小为2.40%,都在10%以内,可以认为该模型合理,能够对粉尘浓度变化进行较好的预测。
3 结 论
1) 影响粉尘浓度的因素有很多,如作业场所、通风系统等,通过分析得出利用时间序列对粉尘浓度预测是可行的。
2) 粉尘浓度是非平稳随机序列,在前人的相关研究基础上,将ARIMA模型运用到粉尘浓度预测方面,结合某矿监测数据,建立ARIMA(1,2,1)预测模型,并对模型进行检验,最后将预测值与实测值进行对比,得到相对误差都控制在10%以内,进一步验证了模型的合理性。
3) 虽然模型精度较高,但是ARIMA模型是基于历史数据的变化趋势对未来进行预测,并不能准确了解到未来环境变化对数据的影响,可见模型对短期预测效果较好,若需要长期预测还要进一步结合其它模型进行研究。

